线性回归简介
线性回归简介
- 1、情景描述
- 2、线性回归
1、情景描述
假设,我们现在有这么一张图:

其中,横坐标x表示房子的面积,纵坐标y表示房价。我们猜想x与y之间存在线性关系: y = k x + b y=kx+b y=kx+b
现在,思考一个问题:如何找到一条直线,使得这条直线尽可能地拟合图中的所有数据点?

这个找最佳拟合直线的过程称为做线性回归
简而言之,线性回归就是在N维空间中找一个类似直线方程y=kx+b一样的函数来拟合数据
线性回归模型则是利用线性函数对一个或多个自变量(x)和因变量(y)之间的关系进行拟合的模型
这里有一个问题,线性等于直线吗?
线性函数的定义是零阶或一阶多项式。特征是二维时,线性模型在二维空间构成一条直线;特征是三维时,线性模型在三维空间中构成一个平面;以此类推,具体见下文线性回归的定义及推导
还有一个问题,那就是如何评判找的哪条直线才是最优的?详见文章最小二乘法:传送门
2、线性回归
1)线性回归的定义及推导
定义:对于一个有n个特征的样本而言,它的线性回归方程如下:
y = f ( x 1 , x 2 , . . . , x n − 1 ) = ω 0 + w 1 x 1 + w 2 x 2 + . . . + w n − 1 x n − 1 y = f(x_1,x_2,...,x_{n-1}) = \omega_0 + w_1x_1 + w_2x_2 +...+w_{n-1}x_{n-1} y=f(x1,x2,...,xn−1)=ω0+w1x1+w2x2+...+wn−1xn−1
其中, w 0 w_0 w0~ w n − 1 w_{n-1} wn−1统称为模型的参数,表示样本有n个特征,有时也用 θ \theta θ或 β \beta β表示
w 0 w_0 w0称为截距, w 1 w_1 w1~ w n − 1 w_{n-1} wn−1称为回归系数(Regression Coefficients), x 1 x_1 x1~ x n − 1 x_{n-1} xn−1为样本的输入向量,y为样本的输出向量
根据简单场景推导n个特征的样本线性回归方程过程如下:
假设我们有2个样本:[ x 1 x_1 x1=1, y 1 y_1 y1=1]、[ x 2 x_2 x2=2, y 2 y_2 y2=3],我们猜测其关系符合:
y = k x + b y = kx + b y=kx+b
将样本代入函数:
{ k ∗ 1 + b = 1 k ∗ 2 + b = 3 \begin{cases} k * 1 + b = 1 \\ k * 2 + b = 3 \end{cases} {k∗1+b=1k∗2+b=3
从最小次幂排列:
{ b ∗ 1 + k ∗ 1 = 1 b ∗ 1 + k ∗ 2 = 3 \begin{cases} b*1 + k*1 = 1 \\ b*1 + k*2 = 3 \end{cases} {b∗1+k∗1=1b∗1+k∗2=3
对应到2个特征的线性回归方程模板:
{ b ∗ x 01 + k ∗ x 11 = y 1 b ∗ x 02 + k ∗ x 12 = y 2 \begin{cases} b*x_{01} + k*x_{11} = y_1 \\ b*x_{02} + k*x_{12} = y_2 \end{cases} {b∗x01+k∗x11=y1b∗x02+k∗x12=y2
转换为矩阵:
[ 1 1 1 2 ] [ b k ] = [ 1 3 ] \left[ \begin{matrix} 1 & 1 \\ 1 & 2 \end{matrix} \right] \left[ \begin{matrix} b \\ k \end{matrix} \right] = \left[ \begin{matrix} 1 \\ 3 \end{matrix} \right] [1112][bk]=[13]
其中, x 0 x_0 x0始终为1。对应到2个特征的线性回归方程模板:
[ 1 x 11 1 x 12 ] [ b k ] = [ y 1 y 2 ] \left[ \begin{matrix} 1 & x_{11} \\ 1 & x_{12} \end{matrix} \right] \left[ \begin{matrix} b \\ k \end{matrix} \right] = \left[ \begin{matrix} y_1 \\ y_2 \end{matrix} \right] [11x11x12][bk]=[y1y2]
推广到一般场景:
[ 1 x 11 x 21 ⋯ x n − 1 , 1 1 x 12 x 22 ⋯ x n − 1 , 2 ⋮ ⋮ ⋮ ⋱ ⋮ 1 x 1 m x 2 m ⋯ x n − 1 , m ] [ ω 0 ω 1 ⋮ ω m − 1 ] = [ y 1 y 2 ⋮ y m ] \left[ \begin{matrix} 1 & x_{11} & x_{21} & \cdots & x_{{n-1},1} \\ 1 & x_{12} & x_{22} & \cdots & x_{{n-1},2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{1m} & x_{2m} & \cdots & x_{{n-1},m} \end{matrix} \right] \left[ \begin{matrix} \omega_0 \\ \omega_1 \\ \vdots \\ \omega_{m-1} \end{matrix} \right] = \left[ \begin{matrix} y_1 \\ y_2 \\ \vdots \\ y_m \end{matrix} \right] 11⋮1x11x12⋮x1mx21x22⋮x2m⋯⋯⋱⋯xn−1,1xn−1,2⋮xn−1,m ω0ω1⋮ωm−1 = y1y2⋮ym
简化:
X ω = y X\omega=y Xω=y
其中,y为m × \times × 1的矩阵向量,表示模型的理论输出; ω \omega ω为n × \times × 1的矩阵向量,表示模型的样本输入;X为m × \times × n的矩阵向量,m表示样本数,n表示样本的特征数
2)线性回归的解
线性回归的解析解 ω \omega ω推导:
假设Y是样本的输出矩阵向量,维度为m × \times × 1,则根据勒让德最小二乘准则有:
J ( ω ) = ∣ ∣ y − Y ∣ ∣ 2 = ∣ ∣ X ω − Y ∣ ∣ 2 = ( X ω − Y ) T ( X ω − Y ) J(\omega) = ||y-Y||^2 = ||X\omega-Y||^2=(X\omega-Y)^T(X\omega-Y) J(ω)=∣∣y−Y∣∣2=∣∣Xω−Y∣∣2=(Xω−Y)T(Xω−Y)
根据数学知识,函数导数为0处取极值:
∂ ∂ ω J ( ω ) = 2 X T X ω − 2 X T Y = 0 \frac{\partial}{\partial\omega}J(\omega)=2X^TX\omega-2X^TY=0 ∂ω∂J(ω)=2XTXω−2XTY=0
解得:
ω = ( X T X ) − 1 X T Y \omega=(X^TX)^{-1}X^TY ω=(XTX)−1XTY
3)线性回归解的几何意义
线性回归的解是通过最小二乘法求解的。其几何意义是:求解 Y Y Y在 X X X的列向量空间中的投影
几何意义的推导后续视情况补充
相关文章:

线性回归简介
线性回归简介 1、情景描述2、线性回归 1、情景描述 假设,我们现在有这么一张图: 其中,横坐标x表示房子的面积,纵坐标y表示房价。我们猜想x与y之间存在线性关系: y k x b ykxb ykxb 现在,思考一个问题&…...
Log4net 教程
一、Log4net 教程 在CodeProject上找到一篇关于Log4net的教程:log4net Tutorial,这篇博客的作者是:Tim Corey ,对应源代码地址为: https://github.com/TimCorey/Log4netTutorial,视频地址为:Ap…...

test-01-java 单元测试框架 junit 入门介绍
JUnit JUnit 是一个用于编写可重复测试的简单框架。 它是 xUnit 架构的一种实例,专门用于单元测试框架。 What to test? NeedDescRight结果是否正确B边界条件是否满足I能反向关联吗C有其他手段交叉检查吗E是否可以强制异常发生P性能问题 maven 入门例子 maven …...

Linux系统中跟TCP相关的系统配置项
TCP连接保活 参考 《Nginx(三) 配置文件详解 - 基础模块》3.18章节 net.ipv4.tcp_keepalive_intvl:设置TCP两次相邻探活检测的间隔时间。默认75秒,单位是秒,对应配置文件/proc/sys/net/ipv4/tcp_keepalive_intvl;net.ipv4.tcp_kee…...

python图片批量下载多线程+超时重试
背景 上篇python入门实战:爬取图片到本地介绍过如何将图片下载到本地,但是实际处理过程中会遇到性能问题:分页数过多下载时间过程、部分页面连接超时无法访问下载失败。本文从实战的角度解释一下如何处理这两个问题。 下载时间过长问题,处理方式是使用多线程,首先回顾…...
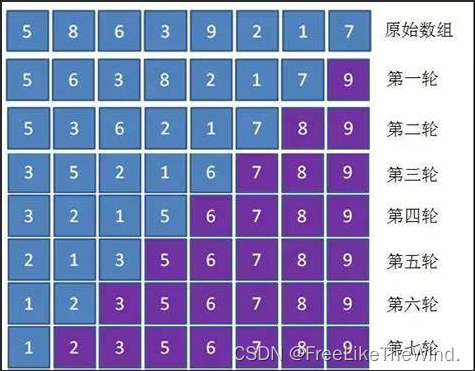
冒泡排序之C++实现
描述 冒泡排序算法是一种简单的排序算法,它通过将相邻的元素进行比较并交换位置来实现排序。冒泡排序的基本思想是,每一轮将未排序部分的最大元素逐个向右移动到已排序部分的最右边,直到所有元素都按照从小到大的顺序排列。 冒泡排序的算法…...

【Spring实战】04 Lombok集成及常用注解
文章目录 0. 集成1. Data2. Getter 和 Setter3. NoArgsConstructor,AllArgsConstructor和RequiredArgsConstructor4. ToString5. EqualsAndHashCode6. NonNull7. Builder总结 Lombok 是一款 Java 开发的工具,它通过注解的方式简化了 Java 代码的编写&…...

ubuntu-22.04.3 配置
1.防火墙 a、查看防火墙状态:inactive是关闭,active是开启。 sudo ufw statusb、开启防火墙。 sudo ufw enablec、关闭防火墙。 sudo ufw disable2.设置Ip ifconfigsudo cp /etc/netplan/00-installer-config.yaml /etc/netplan/00-installer-config.y…...

[工具]java_sublime的快速使用
目录 使用 : 怎么运行: 调整字体: 使用 : 新建--->写好代码后-->另存为尾缀是.java的文件 怎么运行: 在你另存为的目录下cmd调用控制台输入dos指令--->执行javac 文件名.java(有.java尾缀)(编译为.class文件)--->java 文件名(没有.class尾缀设计者认为执行的是…...
【银行测试】银行金融测试+金融项目测试点汇总...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、银行金融测试是…...
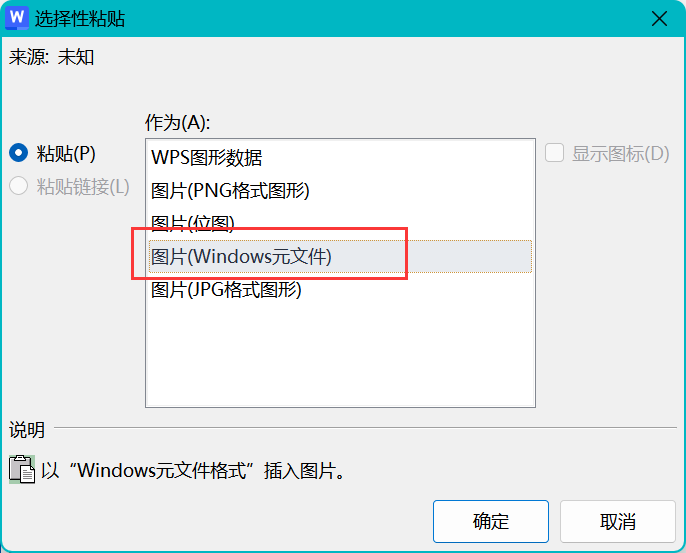
将PPT的图保持高分辨率导入到Word / WPS中
1、将PPT中画好的图组合在一起,选择组合后的图复制(Ctrlc) 2、在Word中,选中左上角的粘贴选项--->选择性粘贴 WPS选择元文件 / Word选择增强型图元文件 这样放大也不模糊了...

如何在Spring Boot中优雅地进行参数校验
1. 前言 在平时的开发工作中,我们通常需要对接口进行参数格式验证。当参数个数较少(个数小于3)时,可以使用if ... else ...手动进行参数验证。当参数个数大于3个时,使用if ... else ...进行参数验证就会让代码显得臃肿…...

图还能有数据库?一文带你了解图数据库是个什么东西!
图数据库 基础 简介 %% 图数据库是图数据库管理系统的简称,是近年来新兴的一种NoSQL数据库使用图形化的模型进行查询的数据库,通过节点、边和属性等方式来表示和存储数据,支持增删改查::CRUD::等操作。图数据库一般用于OLTP系统中…...

力扣思维题——寻找重复数
题目链接:https://leetcode.cn/problems/find-the-duplicate-number/description/?envTypestudy-plan-v2&envIdtop-100-liked 这题的思维难度较大。一种是利用双指针法进行计算环的起点,这种方法在面试里很难说清楚,也很难想到。大致做…...
基于Kubernetes的jenkins上线
1、基于helm 部署jenkins 要求:当前集群配置了storageClass,并已指定默认的storageClass,一般情况下,创建的storageClass即为默认类 指定默认storageClass的方式 # 如果是新创建默认类: apiVersion: storage.k8s.io/v1…...
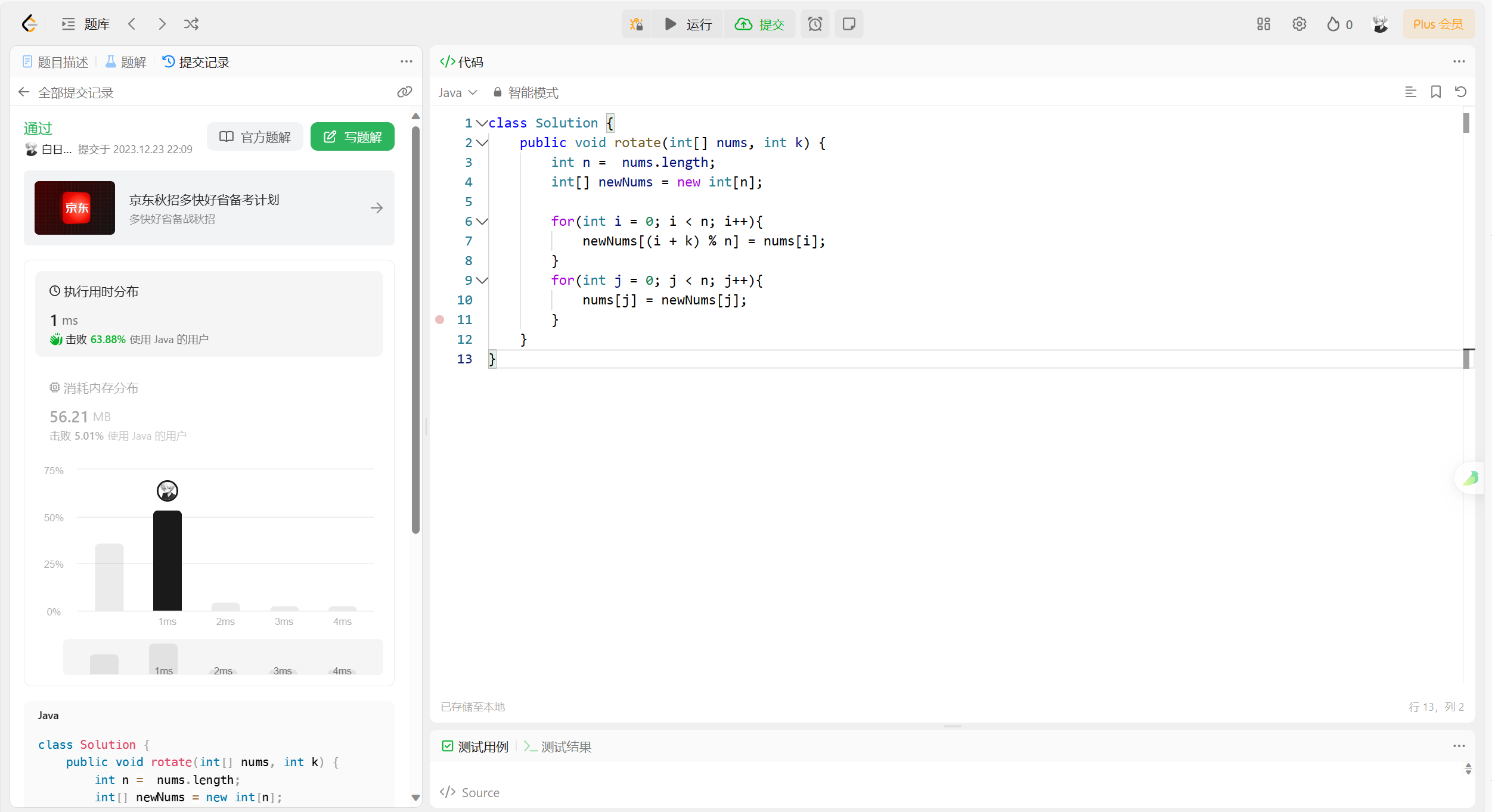
每日一题——轮转数组
1. 题目描述 给定一个整数数组nums,将数组中的元素向右轮转k个位置,其中k是非负数。 示例1: 输入:nums [1,2,3,4,5,6,7],k 3 输出:[5,6,7,1,2,3,4] 解释: 向右轮转 1步:[7,1,2,3,4,5,6] 向右…...
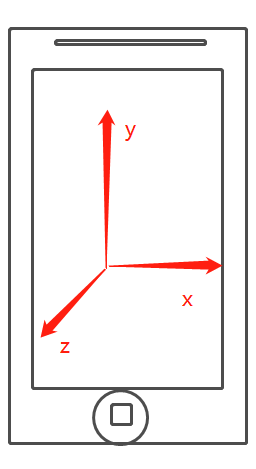
Unity手机移动设备重力感应
Unity手机移动设备重力感应 一、引入二、介绍三、测试成果X Y轴Z轴横屏的手机,如下图竖屏的手机,如下图 一、引入 大家对重力感应应该都不陌生,之前玩过的王者荣耀的资源更新界面就是使用了重力感应的概念,根据手机的晃动来给实体…...
nodejs微信小程序+python+PHP基于推荐算法的电影推荐系统-计算机毕业设计推荐django
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

Linux 配置 swap 区
Linux 配置 swap 区 很多时候我们需要配置 swap 主要的原因是物理内存太贵了, 服务器也是一样, 当内存不够用时, 系统会卡死, 因此我们宁愿牺牲一点性能也要让系统正常运行。 当然, 在系统物理内存足够的条件下&#x…...
AG16KDDF256 User Manual
AGM AG16KDDF256 是由 AGM FPGA AG16K 与 DDR-SDRAM 叠封集成的芯片,具有 AG16K FPGA的可编程功能,提供更多可编程 IO,同时内部连接大容量 DDR-SDRAM。 FPGA 外部管脚 FBGA256 封装,管脚说明请见下表 Table-1: Tab…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
