每日一题——轮转数组

1. 题目描述
给定一个整数数组nums,将数组中的元素向右轮转k个位置,其中k是非负数。
示例1:
输入:nums = [1,2,3,4,5,6,7],k = 3
输出:
[5,6,7,1,2,3,4]解释:
向右轮转 1步:
[7,1,2,3,4,5,6]向右轮转 2步:
[6,7,1,2,3,4,5]向右轮转 3步:
[5,6,7,1,2,3,4]
示例2
输入:nums = [-1,-100,3,99],k = 2
输出:
[3,99,-1,-100]解释:
向右轮转 1步:
[99,-1,-100,3]向右轮转 2步:
[3,99,-1,-100]
提示
-
1 <=
nums.length<= 105 -
-231 <=
nums[i]<= 231 - 1 -
0 <= k <= 105
题目链接
2. 思路
- 定义
n表示数组长度。 - 定义数组
newNums,长度为n。 - 遍历原数组,将原数组下标为
i对的元素放置新数组下标为(i + k) % n的位置。 - 将新数组拷贝至原数组即可。
3. 代码
class Solution {public void rotate(int[] nums, int k) {int n = nums.length;int[] newNums = new int[n];for(int i = 0; i < n; i++){newNums[(i + k) % n] = nums[i];}for(int j = 0; j < n; j++){nums[j] = newNums[j];}}
}
运行结果:
相关文章:

每日一题——轮转数组
1. 题目描述 给定一个整数数组nums,将数组中的元素向右轮转k个位置,其中k是非负数。 示例1: 输入:nums [1,2,3,4,5,6,7],k 3 输出:[5,6,7,1,2,3,4] 解释: 向右轮转 1步:[7,1,2,3,4,5,6] 向右…...
Unity手机移动设备重力感应
Unity手机移动设备重力感应 一、引入二、介绍三、测试成果X Y轴Z轴横屏的手机,如下图竖屏的手机,如下图 一、引入 大家对重力感应应该都不陌生,之前玩过的王者荣耀的资源更新界面就是使用了重力感应的概念,根据手机的晃动来给实体…...
nodejs微信小程序+python+PHP基于推荐算法的电影推荐系统-计算机毕业设计推荐django
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

Linux 配置 swap 区
Linux 配置 swap 区 很多时候我们需要配置 swap 主要的原因是物理内存太贵了, 服务器也是一样, 当内存不够用时, 系统会卡死, 因此我们宁愿牺牲一点性能也要让系统正常运行。 当然, 在系统物理内存足够的条件下&#x…...
AG16KDDF256 User Manual
AGM AG16KDDF256 是由 AGM FPGA AG16K 与 DDR-SDRAM 叠封集成的芯片,具有 AG16K FPGA的可编程功能,提供更多可编程 IO,同时内部连接大容量 DDR-SDRAM。 FPGA 外部管脚 FBGA256 封装,管脚说明请见下表 Table-1: Tab…...
w15初识php基础
一、计算100之内的偶数之和 实现思路 所有的偶数除2都为0 代码实现 <?php # 记录100以内的偶数和 $number1; $num0; while($number<100){if($number%20){ $num$number;}$number1; } echo $num; ?>输出的结果 二、计算100之内的奇数之和 实现思路 所有的奇数除…...

powerbuilder Primary! Delete! Filter! 三个缓冲区的作用
Primary! 主缓存区,放正在使用的数据。 Delete! 删除缓存区,放将要删除但还没有提交到数据库的数据。 Filter! 筛选缓存区,放不符合筛选条件的数据。 最后在update的时候根据你的update设置生成相应的SQL语句。行的状态和所在的缓存区决定生…...

Confluent 与阿里云将携手拓展亚太市场,提供消息流平台服务
10 月 31 日,杭州云栖大会上,阿里云云原生应用平台负责人丁宇宣布,Confluent 成为阿里云技术合作伙伴,合作全新升级,一起拓展和服务亚太市场。 本次合作伙伴签约,阿里云与消息流开创领导者 Confluent 将进一…...
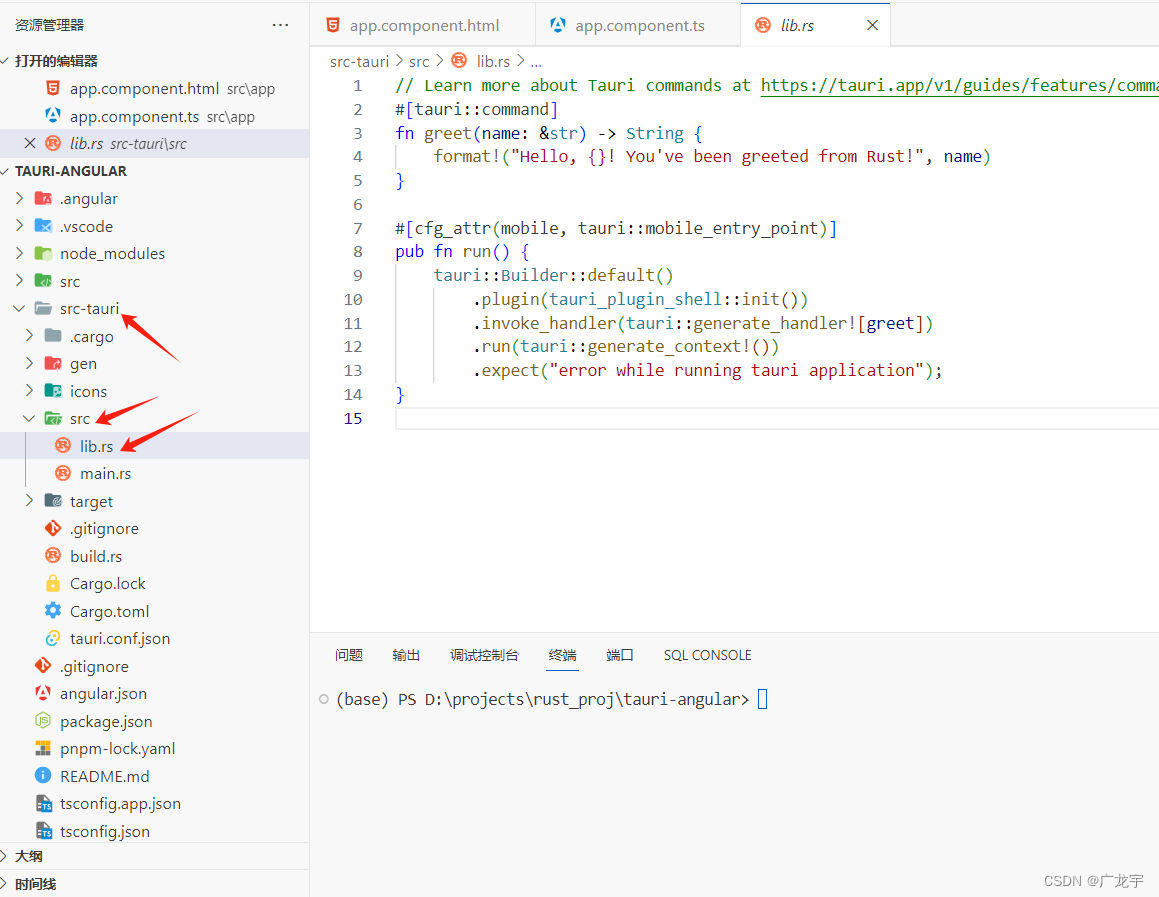
【一起学Rust | 框架篇 | Tauri2.0框架】Tauri2.0环境搭建与项目创建
文章目录 前言一、搭建 Tauri 2.0 开发环境二、创建 Tauri 2.0 项目1.创建项目2.安装依赖4. 编译运行 三、设置开发环境四、项目结构 前言 Tauri在Rust圈内成名已久,凭借Rust的可靠性,使用系统原生的Webview构建更小的App 以及开发人员可以灵活的使用各…...

算法基础之01背包问题
01背包问题 核心思想: 二维数组普通写法: #include<iostream>#include<cstring>#include<algorithm>using namespace std;const int N 1010;int f[N][N]; //存 i个物品 容量不超过j 的总价值int v[N],w[N];int n,m;int main(){cin>>n>…...
Git的总体认知与具体实现
GIt概念 是一种分布式控制管理器 tips:敏捷开发 -> 先上线,后续开发再继续开发 集中式和分布式 集中式的版本控制系统每次在写代码时都需要从服务器中拉取一份下来,并且如果服务器丢失了,那么所有的就都丢失了,你本机客户端仅…...
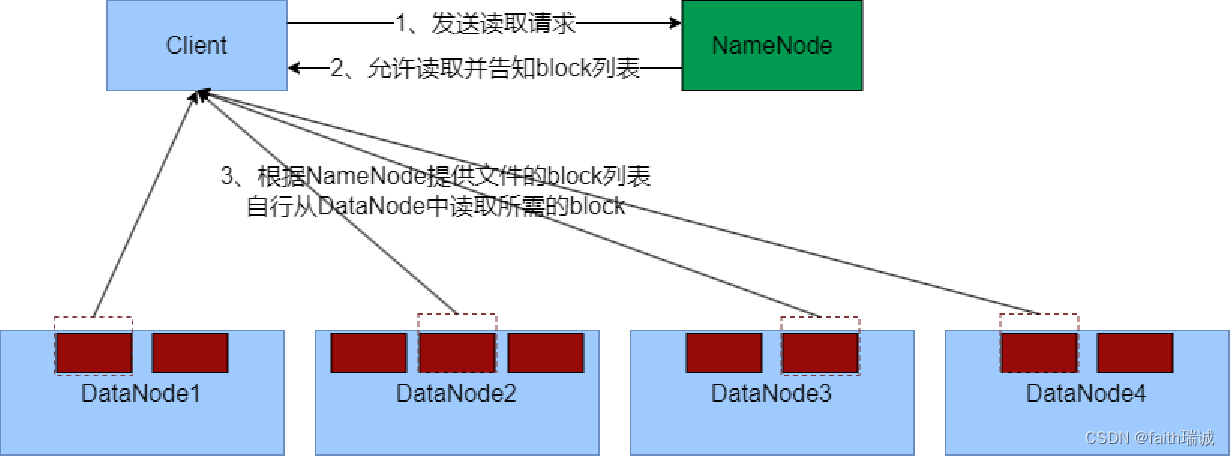
Hadoop入门学习笔记——三、使用HDFS文件系统
视频课程地址:https://www.bilibili.com/video/BV1WY4y197g7 课程资料链接:https://pan.baidu.com/s/15KpnWeKpvExpKmOC8xjmtQ?pwd5ay8 Hadoop入门学习笔记(汇总) 目录 三、使用HDFS文件系统3.1. 使用命令操作HDFS文件系统3.1.…...
JavaWeb—html, css, javascript, dom,xml, tomcatservlet
文章目录 快捷键HTML**常用特殊字符替代:****标题****超链接标签****无序列表、有序列表****无序列表**:ul/li 基本语法**有序列表ol/li:****图像标签(img)**** 表格(table)标签****表格标签-跨行跨列表格****form(表单)标签介绍****表单form提交注意事项**div 标签p 标签sp…...
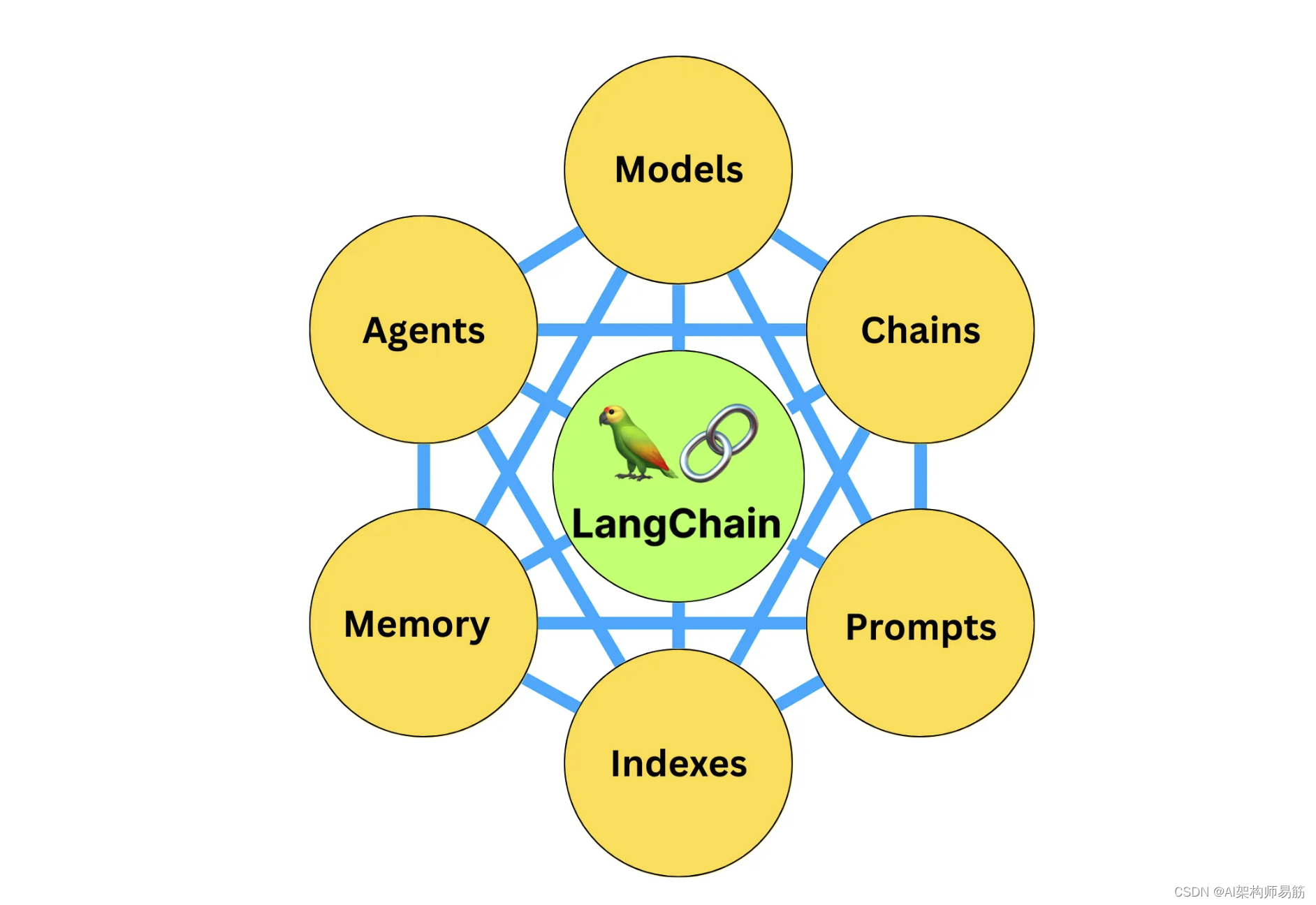
LangChain 31 模块复用Prompt templates 提示词模板
LangChain系列文章 LangChain 实现给动物取名字,LangChain 2模块化prompt template并用streamlit生成网站 实现给动物取名字LangChain 3使用Agent访问Wikipedia和llm-math计算狗的平均年龄LangChain 4用向量数据库Faiss存储,读取YouTube的视频文本搜索I…...
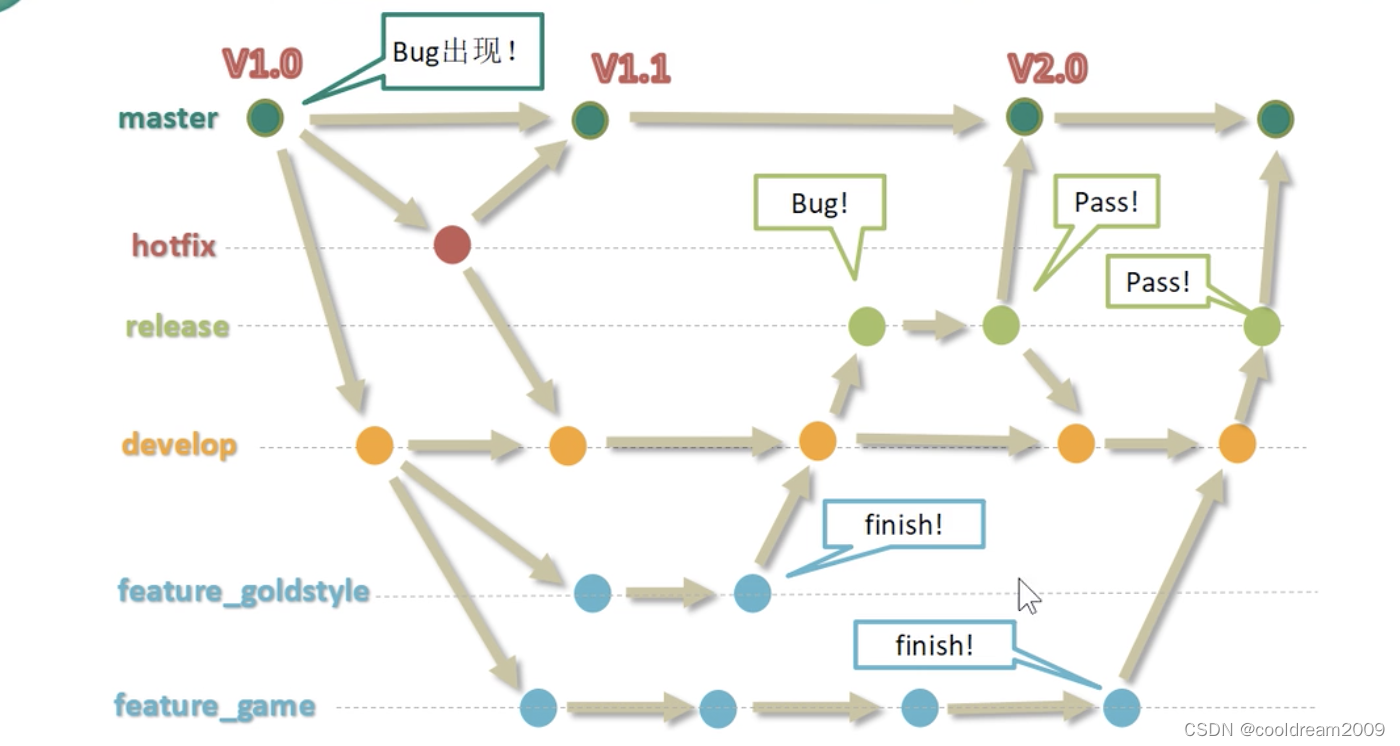
深入理解 Git 分支管理:提升团队协作与开发效率
目录 前言1 什么是分支2 分支的好处2.1 并行开发的支持2.2 独立性与隔离性2.3 灵活的版本控制2.4 提高安全性和代码质量2.5 项目历史的清晰记录 3 Git 分支操作命令3.1 git branch -v3.2 git branch 分支名称3.3 git checkout 分支名称3.4 git merge 分支名称3.5 git rebase 分…...

WPF StackPanel
StackPanel是一个控件容器,它按照一个方向(水平或垂直)堆叠子元素,使得它们沿一个轴线对齐。你可以在StackPanel中放置其他控件,如按钮、标签、文本框、图片等等。这些控件的排列方式由StackPanel按照指定的方向自动确…...
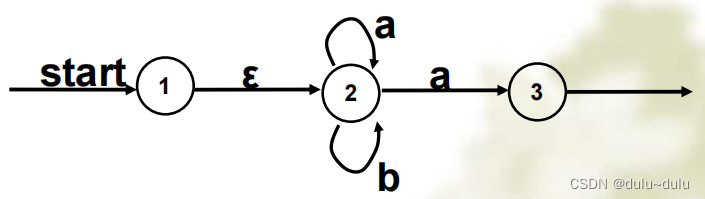
由正规表达式构造DFA,以及DFA的相关化简
目录 1.由正规式到DFA 首先讲如何从正规式到NFA 如何从NFA到DFA 2.DFA的化简 3.DFA和NFA的区别 1.由正规式到DFA 正规式--->NFA---->DFA 首先讲如何从正规式到NFA 转换规则: 例题1:这里圆圈里面的命名是随意的,只要能区别开就可以了 如何…...
:Adaboost)
模式识别与机器学习(九):Adaboost
1.原理 AdaBoost是Adaptive Boosting(自适应增强)的缩写,它的自适应在于:被前一个基本分类器误分类的样本的权值会增大,而正确分类的样本的权值会减小,并再次用来训练下一个基本分类器。同时,在…...
【JAVA】分布式链路追踪技术概论
目录 1.概述 2.基于日志的实现 2.1.实现思想 2.2.sleuth 2.2.可视化 3.基于agent的实现 4.联系作者 1.概述 当采用分布式架构后,一次请求会在多个服务之间流转,组成单次调用链的服务往往都分散在不同的服务器上。这就会带来一个问题:…...
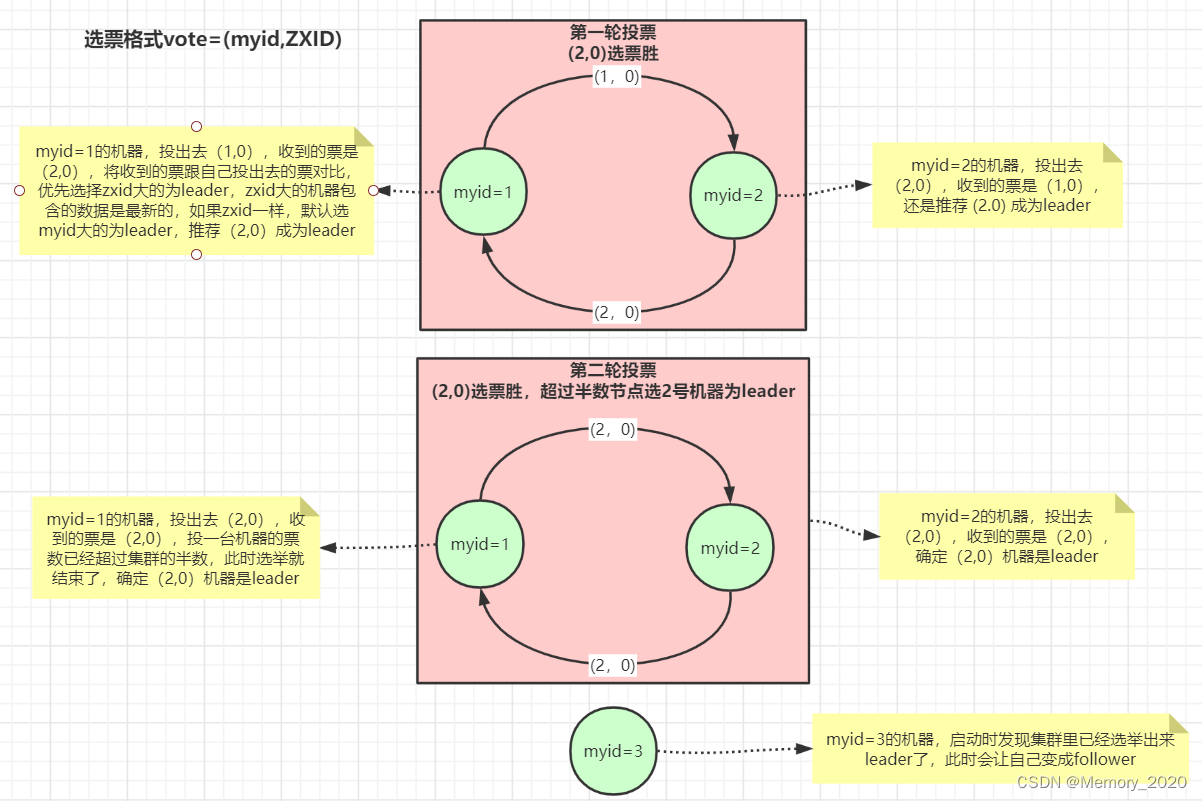
ZooKeeper 使用介绍和原理详解
目录 1. 介绍 重要性 应用场景 2. ZooKeeper 架构 服务角色 数据模型 工作原理 3. 安装和配置 下载 ZooKeeper 安装和配置 启动 ZooKeeper 验证和管理 停止和关闭 4. ZooKeeper 数据模型 数据结构和层次命名空间: 节点类型和 Watcher 机制ÿ…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
