代码随想录算法训练营day47 |动态规划 198打家劫舍 213打家劫舍II 337打家劫舍III
day47
- 198.打家劫舍
- 1.确定dp数组(dp table)以及下标的含义
- 2.确定递推公式
- 3.dp数组如何初始化
- 4.确定遍历顺序
- 5.举例推导dp数组
- 213.打家劫舍II
- 情况一:考虑不包含首尾元素
- 情况二:考虑包含首元素,不包含尾元素
- 情况三:考虑包含尾元素,不包含首元素
- 337.打家劫舍III
- 1.确定递归函数的参数和返回值
- 2.确定终止条件
- 3.确定遍历顺序
- 4.确定单层递归的逻辑
- 5.举例推导dp数组
198.打家劫舍
题目链接
解题思路: 当前状态和前面状态会有一种依赖关系,那么这种依赖关系都是动规的递推公式。
动规五部曲分析如下:
1.确定dp数组(dp table)以及下标的含义
dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。
2.确定递推公式
决定dp[i]的因素就是第i房间偷还是不偷。
如果偷第i房间,那么dp[i] = dp[i - 2] + nums[i] ,即:第i-1房一定是不考虑的,找出下标i-2(包括i-2)以内的房屋,最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
如果不偷第i房间,那么dp[i] = dp[i - 1],即考 虑i-1房,(注意这里是考虑,并不是一定要偷i-1房,这是容易混淆的点)
然后dp[i]取最大值,即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
3.dp数组如何初始化
从递推公式dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);可以看出,递推公式的基础就是dp[0] 和 dp[1]
从dp[i]的定义上来讲,dp[0] 一定是 nums[0],dp[1]就是nums[0]和nums[1]的最大值即:dp[1] = max(nums[0], nums[1]);
代码如下:
vector<int> dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
4.确定遍历顺序
dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,那么一定是从前到后遍历!
代码如下:
for (int i = 2; i < nums.size(); i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
5.举例推导dp数组
以示例二,输入[2,7,9,3,1]为例。
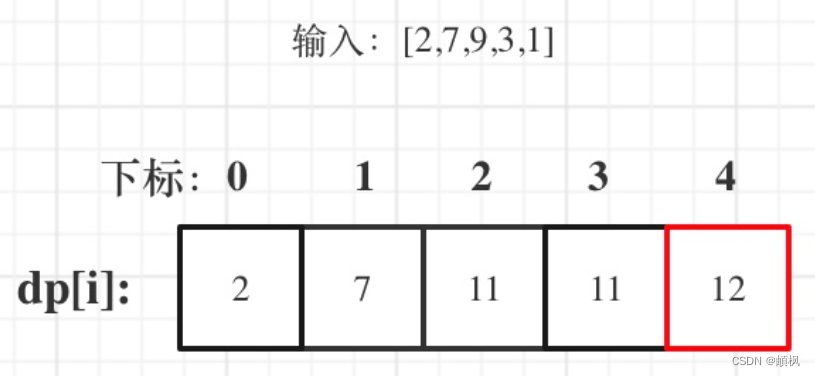 红框
红框dp[nums.size() - 1]为结果。
以上分析完毕,C++代码如下:
class Solution {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];vector<int> dp(nums.size());dp[0] = nums[0];dp[1] = max(nums[0], nums[1]);for (int i = 2; i < nums.size(); i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[nums.size() - 1];}
};213.打家劫舍II
题目链接
解题思路:
和198 打家劫舍1 相比,唯一区别就是成环了。
对于一个数组,成环的话主要有如下三种情况:
情况一:考虑不包含首尾元素
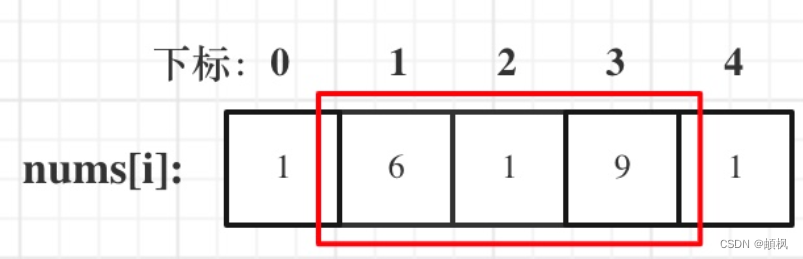
情况二:考虑包含首元素,不包含尾元素
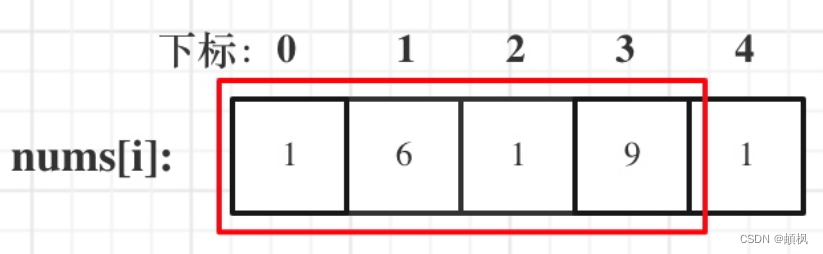
情况三:考虑包含尾元素,不包含首元素
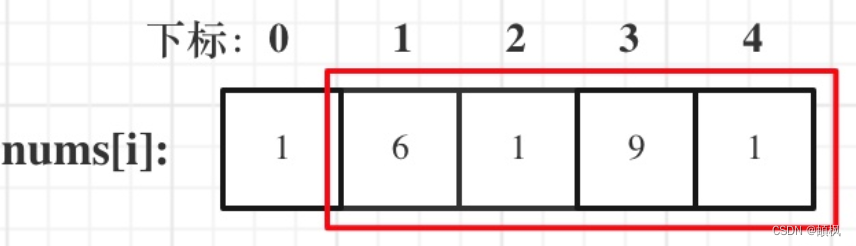
情况三中,虽然是考虑包含尾元素,但不一定要选尾部元素! 对于情况三,取nums[1] 和 nums[3]就是最大的。
而情况二 和 情况三 都包含了情况一了,所以只考虑情况二和情况三就可以了。
代码如下:
// 注意注释中的情况二情况三,以及把198.打家劫舍的代码抽离出来了
class Solution {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];int result1 = robRange(nums, 0, nums.size() - 2); // 情况二int result2 = robRange(nums, 1, nums.size() - 1); // 情况三return max(result1, result2);}// 198.打家劫舍的逻辑int robRange(vector<int>& nums, int start, int end) {if (end == start) return nums[start];vector<int> dp(nums.size());dp[start] = nums[start];dp[start + 1] = max(nums[start], nums[start + 1]);for (int i = start + 2; i <= end; i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[end];}
};
337.打家劫舍III
解题思路:
这道题目算是树形dp的入门题目,因为是在树上进行状态转移,我们在讲解二叉树的时候说过递归三部曲,那么下面我以递归三部曲为框架,其中融合动规五部曲的内容来进行讲解。
1.确定递归函数的参数和返回值
这里我们要求一个节点 偷与不偷的两个状态所得到的金钱,那么返回值就是一个长度为2的数组。
参数为当前节点,代码如下:
vector<int> robTree(TreeNode* cur) {
其实这里的返回数组就是dp数组。
所以dp数组(dp table)以及下标的含义:下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱。
所以本题dp数组就是一个长度为2的数组!
那么有同学可能疑惑,长度为2的数组怎么标记树中每个节点的状态呢?
别忘了在递归的过程中,系统栈会保存每一层递归的参数。
如果还不理解的话,就接着往下看,看到代码就理解了哈。
2.确定终止条件
在遍历的过程中,如果遇到空节点的话,很明显,无论偷还是不偷都是0,所以就返回
if (cur == NULL) return vector<int>{0, 0};
这也相当于dp数组的初始化
3.确定遍历顺序
首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。
通过递归左节点,得到左节点偷与不偷的金钱。
通过递归右节点,得到右节点偷与不偷的金钱。
代码如下:
// 下标0:不偷,下标1:偷
vector<int> left = robTree(cur->left); // 左
vector<int> right = robTree(cur->right); // 右
// 中
4.确定单层递归的逻辑
如果是偷当前节点,那么左右孩子就不能偷,val1 = cur->val + left[0] + right[0]; (如果对下标含义不理解就再回顾一下dp数组的含义)
如果不偷当前节点,那么左右孩子就可以偷,至于到底偷不偷一定是选一个最大的,所以:val2 = max(left[0], left[1]) + max(right[0], right[1]);
最后当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱}
代码如下:
vector<int> left = robTree(cur->left); // 左
vector<int> right = robTree(cur->right); // 右// 偷cur
int val1 = cur->val + left[0] + right[0];
// 不偷cur
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return {val2, val1};
5.举例推导dp数组
以示例1为例,dp数组状态如下:(注意用后序遍历的方式推导)
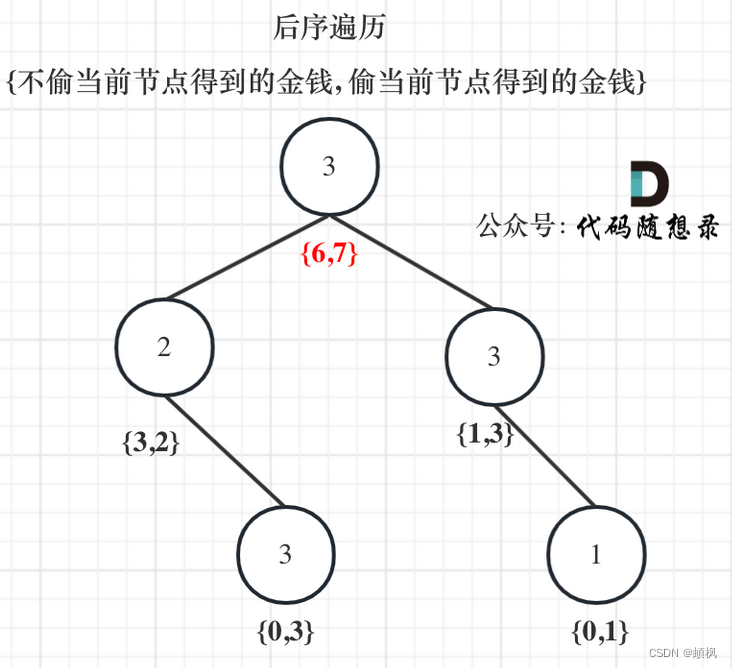
最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱。
递归三部曲与动规五部曲分析完毕,C++代码如下:
class Solution {
public:int rob(TreeNode* root) {vector<int> result = robTree(root);return max(result[0], result[1]);}// 长度为2的数组,0:不偷,1:偷vector<int> robTree(TreeNode* cur) {if (cur == NULL) return vector<int>{0, 0};vector<int> left = robTree(cur->left);vector<int> right = robTree(cur->right);// 偷cur,那么就不能偷左右节点。int val1 = cur->val + left[0] + right[0];// 不偷cur,那么可以偷也可以不偷左右节点,则取较大的情况int val2 = max(left[0], left[1]) + max(right[0], right[1]);return {val2, val1};}
};
相关文章:

代码随想录算法训练营day47 |动态规划 198打家劫舍 213打家劫舍II 337打家劫舍III
day47198.打家劫舍1.确定dp数组(dp table)以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组213.打家劫舍II情况一:考虑不包含首尾元素情况二:考虑包含首元素,不包含尾元素情况三&#x…...
项目设计模式和规范
1、责任链模式 自己的理解:避免发生方与接收方解耦 优点:①降低发送方与接收方的耦合 ②简化他们对象 ③方便扩展新增 处理者 缺点:①不方便排错 ②性能问题,且使用不当容易搞出死循环 应用场景:拦截器 Interceptor和过滤器 filter:符合模式的进行拦截或者过滤到,然…...

无线WiFi安全渗透与攻防(一)之无线安全环境搭建
无线安全环境搭建 1.802.11标准 (1).概念 802.11标准是1997年IEEE最初制定的一个WLAN标准,工作在2.4GHz开放频段,支持1Mbit/s和2Mbit/s的数据传输速率,定义了物理层和MAC层规范,允许无线局域网及无线设备…...
【matplotlib】可视化解决方案——如何解决matplotlib中文乱码问题
问题概述 Matplotlib 默认不支持中文字体,这是因为 matplotlib 只支持 ASCII 字符,但是国人使用 matplotlib 肯定需要中文标注。如下图所示,当不对 Matplotlib 进行设置,而直接使用中文时,绘制的图像会出现中文乱码。…...
JAVA开发中GC日志打印简单通用的配置详解
如何配置一个完美的JVM日志打印信息 打印内容 打印基本的GC信息 打印对象分布情况 GC后打印堆数据 打印STW时间 打印safepoint信息 打印Reference处理信息 综上所述,最终的参数如下: 还有哪些问题呢?是不是有文件输出更好? 打印日…...

十进制的小数如何转二进制?二进制表示的小数如何转十进制?
😄 基础不牢,地动山摇~ 补补基础~ 文章目录 1、十进制的小数转二进制?2、二进制表示的小数转十进制?3、做道coding题巩固下:1、十进制的小数转二进制? 整数部分: 用普通的二进制表示即可。小数部分: 首先,将小数部分乘以2,取出整数部分作为二进制表示的第1位;然后…...
klipper使用webcam设置多个摄像头方式
一、前言 使用klipper设置多个摄像头,折腾了好些天,网上资料很少,这里写一个帖子记录一下 二、环境 参考链接:https://www.cnblogs.com/sjqlwy/p/klipper_webcam.html 我的klipper安装在香橙派上面,系统是debian&a…...

风力发电机组浪涌保护器安全防护方案
风机的庞大与危险高空作业注定了其在基建和维护中不易操作,风机设备的主电源、过程控制、网络与通讯、现场设备需要高等级的防雷浪涌保护器冲击保护,提高系统及设备的可靠性和可用性。风电场的主要发电设备风力发电机组“大风车”是风电场的主要发电设备…...
【剑指offer】JZ7 重建二叉树、JZ9 用两个栈实现队列
\描述: 给定节点数为 n 的二叉树的前序遍历和中序遍历结果,请重建出该二叉树并返回它的头结点。 例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建出如下图所示。 思路: 题上给了我们前序遍历(根 …...

ElasticSearch - SpringBoot整合ES之查询所有 match_all
文章目录1. 数据准备2. 全量查询 match_all3. 使用 boost 参数更改 _score官方文档地址:https://www.elastic.co/guide/en/elasticsearch/reference/index.html权威指南:https://www.elastic.co/guide/cn/elasticsearch/guide/current/structured-search…...
详谈IIC
前言 在嵌入式底层系统中,常见的通讯方式,串口,IIC,SPI,IIS等,一般IIC,SPI,IIS更多的采取IO模拟,其余CAN,UART均是硬件设计直接支持,而IIC主要用于多数传感器数据的读写,…...
【Autoware】采集实验数据bag包并仿真运行
文章目录1. 官方demo包2. 控制底层地图采集3. 感知定位4. 规划控制5. 仿真或实车运行1. 官方demo包 wget http://db3.ertl.jp/autoware/sample_data/sample_moriyama_data.tar.gz wget http://db3.ertl.jp/autoware/sample_data/sample_moriyama_150324.tar.gz官方示例包的网上…...

名创优品怎么把创意做成生意?
最近,“主”无处不在,从让“依托答辩”梗火出圈的动画《三体》,到备受好评的电视剧《三体》,再到仍在刷新高票房成绩的《流浪地球2》。作为近些年来中国为数不多的爆款IP制造者,刘慈欣在《三体》中提出了一个著名的理论…...
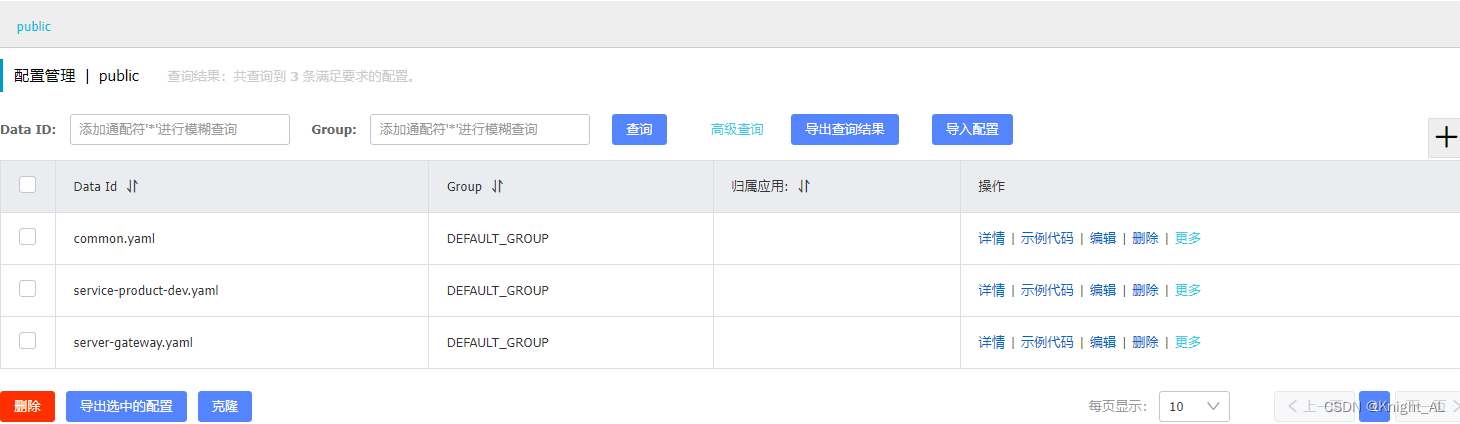
springboot原项目配置文件迁移至nacos
目录一、配置文件迁移nacos1.安装nacos2.添加依赖3.改造service-product3.改造server-gateway一、配置文件迁移nacos 1.安装nacos 1,如果之前安装过nacos,nacos数据保存至mysql,先删除已安装的nacos,再安装 docker stop nacos …...
常用的shell脚步操作
文章目录一、如何开始一个shell脚本?1.基本语法2.变量定义规则二、特色变量1.$n2.$?三、条件判断1.基本语法2.运算符if,for,while四、字符串切割1.从指定位置开始截取从字符串左边开始计数从右边开始计数2.从指定字符(子字符串)开…...

Java on VS Code 2月更新|JUnit 5 并行测试与 Spring Boot 插件的过滤功能
作者:Nick Zhu - Senior Program Manager, Developer Division at Microsoft 排版:Alan Wang 大家好,欢迎来到我们的二月更新!在此博客中,我们将为您带来与 JUnit 5 并行测试相关的新功能以及用于 Spring Boot Dashboa…...
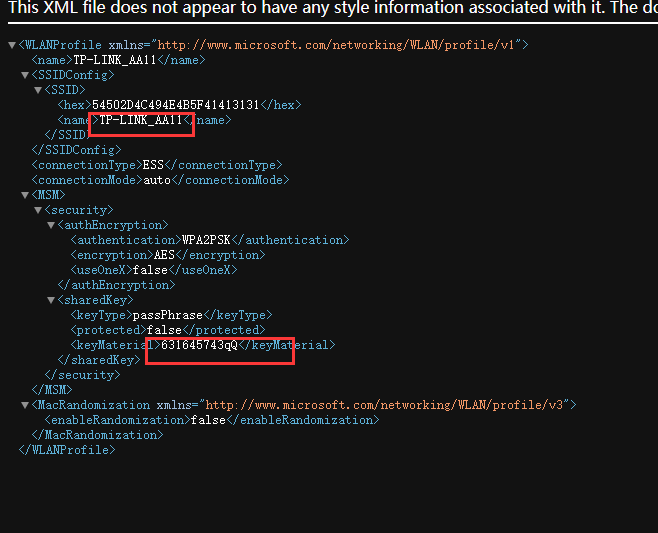
无线WiFi安全渗透与攻防(三)之Windows扫描wifi和破解WiFi密码
系列文章 无线WiFi安全渗透与攻防(一)之无线安全环境搭建 无线WiFi安全渗透与攻防(二)之打造专属字典 windows下wifi进行扫描和破解 1.wifi扫描 (1).软件介绍 WirelessMon是一款无线网络扫描工具,它可以帮助用户扫描附近的无线信号&…...

Python中的遍历字典的键和值
一、Python的字典在项目的开发过程中,如果遇到有映射关系的内容可以考虑使用Python中的字典进行存储数据,字典中冒号前的数据称为【键】、冒号后的数据称为【值】。二、Python字典的用法2.1、Python的定义#Python字典的定义 字典名称{键1:值1,键2:值2,键…...

三天Golang快速入门—结构体
Struct结构体什么是结构体结构体定义基本实例化new实例化键值对初始化结构体方法和接收者结构体说明结构体方法和接收者值类型和指针类型接收者struct与jsonstruct转json字符串json转structstruct tagTag结构体转化Json字符串Json字符串转成Tag结构体什么是结构体 1.Golang中没…...

日常算法刷题——力扣704
##2023/3/2 刷算法的第一天 针对力扣的704题:本题是二分查找的基本使用!在此需要注意二分查找的基本特点: 1.数列基本有序; 2.数列数据内容不可重复。 此题只需了解二分查找算法的基本概念,无坑可跳。但在力扣上刷题就…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
