向量投影:如何将一个向量投影到矩阵的行向量生成子空间?
向量投影:如何将一个向量投影到矩阵的行向量生成子空间?
前言
本问题是在学习Rosen梯度投影优化方法的时候遇到的问题,主要是对于正交投影矩阵(NT(NNT)-1N)的不理解,因此经过查阅资料,学习了关于向量投影的知识,记录如下。
首先需要了解 子空间和子空间的正交补。相关知识可以查阅本人的另外一篇笔记,核和值域的关系:什么是矩阵的秩?,这篇笔记中是以矩阵列向量的生成子空间为例展开的。
核心公式:
- R ( A H ) ∩ N ( A ) = { 0 } R(A^H) \cap N(A)=\{0\} R(AH)∩N(A)={0}
- R ( A H ) ⊕ N ( A ) = C m R(A^H) \oplus N(A) = C^m R(AH)⊕N(A)=Cm
其中R(AH)是A的行向量的生成子空间, R ( A H ) = { y ∈ R n ∣ y = A H x , x ∈ C m } R(A^H)=\{y\in R^n|y=A^Hx,x\in C^m\} R(AH)={y∈Rn∣y=AHx,x∈Cm}。
N(A)是A的核子空间, N ( A ) = { x ∣ A x = 0 , x ∈ R n } N(A)=\{x|Ax=0,x\in R^n\} N(A)={x∣Ax=0,x∈Rn}。
正文
所谓向量投影,本质上是期望将Rn空间中的任意一个n维向量,分解称为y1+y2,其中y1属于R(AH),y2属于N(A)。
1、投影矩阵
投影是一种线性变换,要求两次投影变换的结果等于一次投影变换的结果。在信号处理领域当中,一个信号经过两次滤波器和经过一次滤波器的结果是相等的,那么这个滤波器在数学上可抽象成一个投影矩阵。
写成数学公式: P 2 x = P P x = P x P^2x=PPx=Px P2x=PPx=Px。因此要求投影矩阵P是一个方阵。
可证明:R§=R(PH)。通常情况下一个方阵的行空间和列空间是不相同的,二者仅仅是同构关系,即维数相同。
即: R ( P ) ⊕ N ( P ) = C n R(P) \oplus N(P) = C^n R(P)⊕N(P)=Cn
投影分为正交投影和斜投影。二者的区别在于,正交投影矩阵P,R§的正交补=N§,等价于,R§和N§正交。而斜投影矩阵则没有这个性质。
可证明:一个投影矩阵P,是正交投影矩阵的充要条件是:P=PH
举一个简单的例子。
R2空间,向x轴的正交投影P,只能是取一个二维向量的横坐标。R§就是x轴,N§就是y轴,x轴的正交补是y轴。
R2空间,向x轴的斜投影Q,比如是指向东偏南45度➘方向的的投影。R(Q)就是x轴,x轴的正交补是y轴,而N(Q)是沿着东偏南45度➘方向的一维子空间,即N(Q)={ x|x = a(1,-1)T, a \in R}。
2、如何将一个向量投影到行满秩矩阵A的行向量生成子空间?
现在已知一个行满秩矩阵 A m m × n A^{m\times n}_m Amm×n,R(AH)是由A的行向量生成的子空间。由上面的例子,可以猜到,n维欧氏空间向R(AH)的正交投影是唯一的,斜投影是不唯一的(此处考虑典型情况,而非考虑A行列满秩的极端情况)。
现在推导一个由A构成的正交投影矩阵P。
- y = y 1 + y 2 , y 1 ∈ R ( A H ) , y 2 ∈ R ⊥ ( A H ) y=y_1+y_2,y_1\in R(A^H),y_2\in R^\perp(A^H) y=y1+y2,y1∈R(AH),y2∈R⊥(AH)
- P y = P ( y 1 + y 2 ) = y 1 Py=P(y_1+y_2)=y_1 Py=P(y1+y2)=y1
- y 1 ∈ R ( A H ) , ∴ y 1 = A H x y_1\in R(A^H),\therefore y_1=A^Hx y1∈R(AH),∴y1=AHx,x是一个m维的列向量,即y1可表示为A的行向量的线性组合
- y 2 ∈ R ⊥ ( A H ) = N ( A ) , A y 2 = 0 , A y = A A H x y_2\in R^\perp(A^H)=N(A),Ay_2=0,Ay=AA^Hx y2∈R⊥(AH)=N(A),Ay2=0,Ay=AAHx
- x = ( A A H ) − 1 A y , y 1 = [ A H ( A A H ) − 1 A ] y x=(AA^H)^{-1}Ay,y_1 = [A^H(AA^H)^{-1}A]y x=(AAH)−1Ay,y1=[AH(AAH)−1A]y
- P = A H ( A A H ) − 1 A = P H P = A^H(AA^H)^{-1}A=P^H P=AH(AAH)−1A=PH
从第5步可以知道为什么需要A行满秩了,只有行满秩的矩阵, y 1 ∈ R ( A H ) , y 1 = A H x y_1\in R(A^H),y_1=A^Hx y1∈R(AH),y1=AHx,其中x才有唯一解。
至此,我们知道 P = A H ( A A H ) − 1 A P = A^H(AA^H)^{-1}A P=AH(AAH)−1A是一个正交投影矩阵,将一个向量投影到A的行向量的生成子空间。
3、关于Rosen梯度投影法
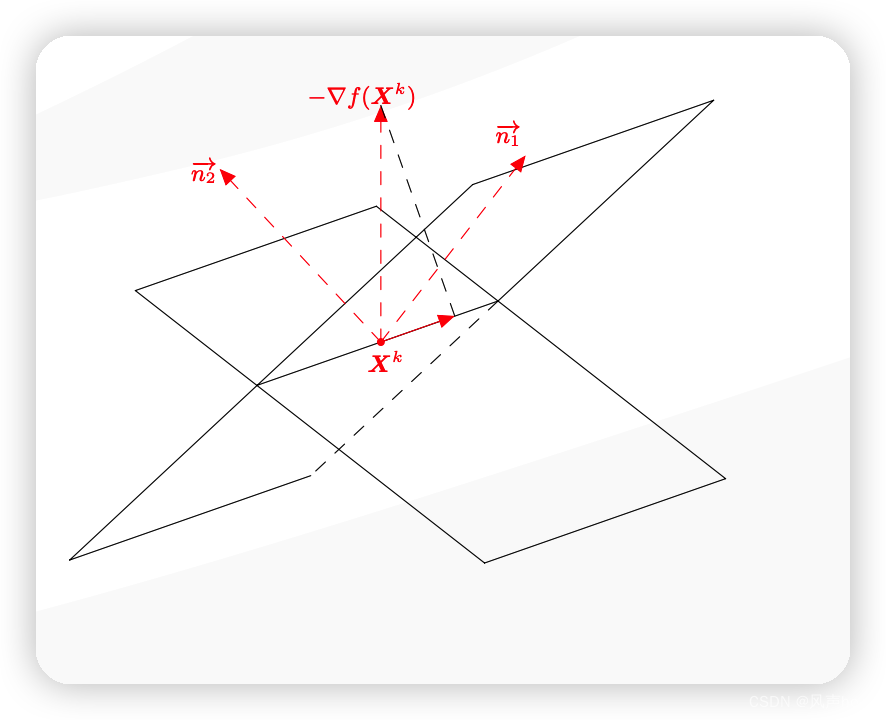
Rosen梯度投影法的可行下降方向: P k = Q ( − g k ) = ( I − N T ( N N T ) − 1 N ) g k P^k = Q(-g^k) = (I-N^T(NN^T)^{-1}N)g^k Pk=Q(−gk)=(I−NT(NNT)−1N)gk
Q是一个投影矩阵,并且投向 N T ( N N T ) − 1 N N^T(NN^T)^{-1}N NT(NNT)−1N的正交补空间,N是由积极约束的法向量组成的矩阵,因此P是负梯度方向向积极约束的法向量张成的行空间的正交补的投影。从几何上看,就是将负梯度方向投影向了积极约束的超平面的交线上。
需要注意,Rosen梯度投影法的约束条件是一个多面集。
相关文章:

向量投影:如何将一个向量投影到矩阵的行向量生成子空间?
向量投影:如何将一个向量投影到矩阵的行向量生成子空间? 前言 本问题是在学习Rosen梯度投影优化方法的时候遇到的问题,主要是对于正交投影矩阵(NT(NNT)-1N)的不理解,因此经过查阅资料,学习了关于向量投影的知识&…...
)
Ubuntu18.04安装GTSAM库(亲测可用)
在SLAM(Simultaneous Localization and Mapping)和SFM(Structure from Motion)这些复杂的估计问题中,因子图算法以其高效和灵活性而脱颖而出,成为图模型领域的核心技术。GTSAM(Georgia Tech Smo…...

SpringBoot中常见配置配置,MySQL、Redis、MinIO等
SpringBoot中配置 启动端口号 server:port: 8501 spring:application:name: server-managerprofiles:active: dev # 当前使用的配置文件servlet:multipart:max-file-size: 20MB # 最大文件max-request-size: 20MB# # 最大请求数据库相关 MySQL spring:datasource:type: com…...

面向LLM的App架构——技术维度
这是两篇面向LLM的大前端架构的第二篇,主要写我对LLM辅助开发能力的认知以及由此推演出的适合LLM辅助开发的技术架构。 LLM之于代码 商业代码对质量的要求其实对LLM是有点高的。主要是输入准确度、输出准确度(这个是绝大部分人质疑的点)、知…...
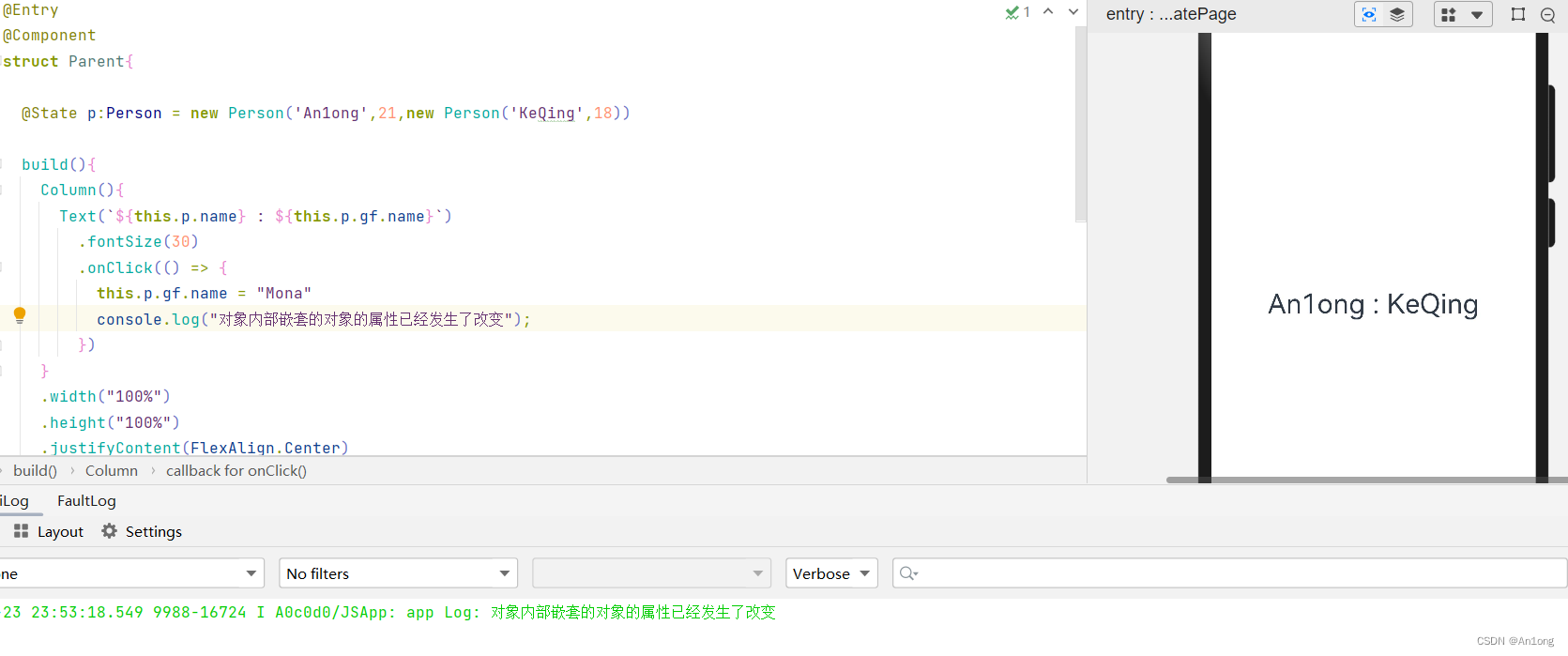
ArkUI - 状态管理
目录 一、State装饰器 二、自定义组件 三、Prop和Link、Provide和Consume 四、Observed和ObjectLink 一、State装饰器 这里涉及到两个概念 状态 和 视图 状态(State):指驱动视图更新的数据(就是被State注解标记的变量&…...

C++ 学习系列 -- C++ 中的多态行为
一 多态是什么? 多态是面向对象三大特征中重要一项,另外两项分别是封装与继承。 所谓多态,指的是多种不同的形态,也就是去完成某个具体的行为,多个不同的对象去操作同一个函数时,会产生不同的行为&…...

Spring Cloud中实现Feign声明式服务调用客户端
可以通过OpenFeign从一个服务中调用另一个服务,我们一般采用的方式就是定义一个Feign接口并使用FeignClient注解来进行标注,feign会默认为我们创建的接口生成一个代理对象。 当我们在代码中调用Feign接口的方法的时候,实际上就是在调用我们Fe…...

【网络编程】网络通信基础——简述TCP/IP协议
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【网络编程】【Java系列】 本专栏旨在分享学习网络编程的一点学习心得,欢迎大家在评论区交流讨论💌 目录 一、ip地…...

观察者模式 Observer
观察者模式属于行为型模式。在程序设计中,观察者模式通常由两个对象组成:观察者和被观察者。当被观察者状态发生改变时,它会通知所有的观察者对象,使他们能够及时做出响应。 三要素:观察者(Observer&#…...
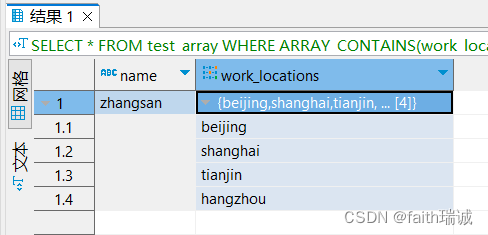
Hadoop入门学习笔记——七、Hive语法
视频课程地址:https://www.bilibili.com/video/BV1WY4y197g7 课程资料链接:https://pan.baidu.com/s/15KpnWeKpvExpKmOC8xjmtQ?pwd5ay8 Hadoop入门学习笔记(汇总) 目录 七、Hive语法7.1. 数据库相关操作7.1.1. 创建数据库7.1.2…...

采用SpringBoot框架+原生HTML、JS前后端分离模式开发和部署的电子病历编辑器源码(电子病历评级4级)
概述: 电子病历是指医务人员在医疗活动过程中,使用医疗机构信息系统生成的文字、符号、图表、图形、数据、影像等数字化信息,并能实现存储、管理、传输和重现的医疗记录,是病历的一种记录形式。 医院通过电子病历以电子化方式记录患者就诊的信息,包括&…...

HTML表单
<!DOCTYPE html> <html><head><meta charset"utf-8"><title>招聘案列</title></head><body><h1>午睡操场传来蝉的声音</h1><hr /><form>昵称:<input type"text" …...

Http 请求体和响应体中重要的字段
Http 请求体 Accept:用于告诉服务器客户端能够处理哪些媒体类型。Accept 头中的值通常是一个或多个 MIME 类型,并按优先级排序。服务器会根据 Accept 头中的值来决定响应的内容类型。例如,Accept: text/plain, text/html。Content-Type&…...
最新国内可用使用GPT4.0,GPT语音对话,Midjourney绘画,DALL-E3文生图
一、前言 ChatGPT3.5、GPT4.0、GPT语音对话、Midjourney绘画,相信对大家应该不感到陌生吧?简单来说,GPT-4技术比之前的GPT-3.5相对来说更加智能,会根据用户的要求生成多种内容甚至也可以和用户进行创作交流。 然而,GP…...
【量化金融】证券投资学
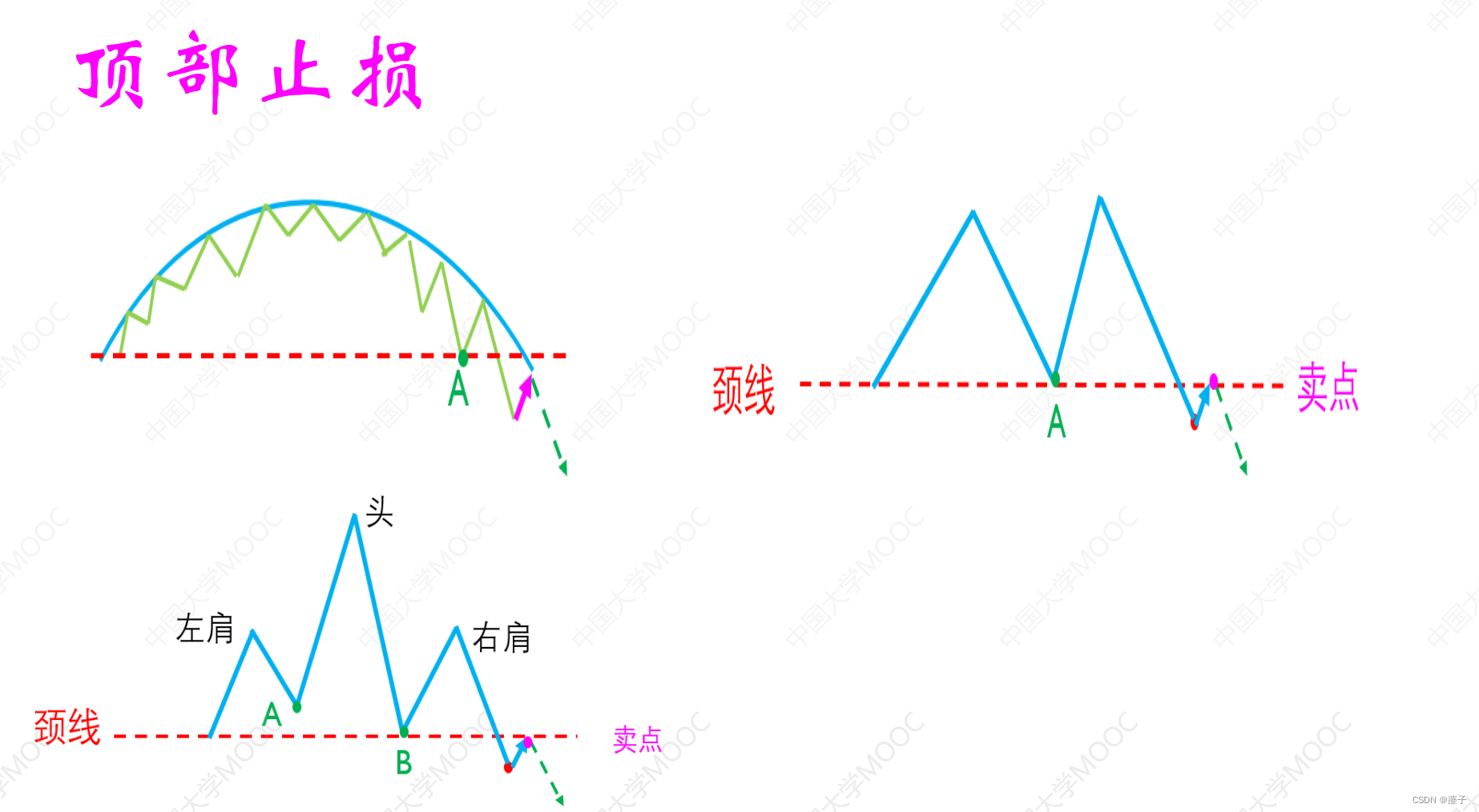
韭菜的自我修养 第一章: 基本框架和概念1.1 大盘底部形成的技术条件1.2 牛市与熊市1.3 交易系统1.3.1 树懒型交易系统1.3.2 止损止损的4个技术 第二章:证券家族4兄弟2.1 债券(1)债券,是伟大的创新(2&#x…...

【Bash】重点总结
文章目录 1. 总体认识1.1. Shell概述1.2. 第一个Shell脚本 2. 变量2.1. 定义变量2.2. 使用变量2.3. 只读变量2.4. 删除变量2.5. 变量类型2.5.1. 字符串变量 1. 总体认识 1.1. Shell概述 Shell是一个用C语言编写的程序,这个程序提供了一个界面,用户通过…...

Git安装和使用教程,并以gitee为例实现远程连接远程仓库
文章目录 1、Git简介及安装2、使用方法2.1、Git的启动与配置2.2、基本操作2.2.1、搭建自己的workspace2.2.2、git add2.2.3、git commit2.2.4、忽略某些文件不予提交2.2.5、以gitee为例实现git连接gitee远程仓库来托管代码 1、Git简介及安装 版本控制(Revision cont…...
Hadoop入门学习笔记——一、VMware准备Linux虚拟机
视频课程地址:https://www.bilibili.com/video/BV1WY4y197g7 课程资料链接:https://pan.baidu.com/s/15KpnWeKpvExpKmOC8xjmtQ?pwd5ay8 Hadoop入门学习笔记(汇总) 目录 一、VMware准备Linux虚拟机1.1. VMware安装Linux虚拟机1.…...

CSS3新增特性
CSS3 CSS3私有前缀 W3C 标准所提出的某个CSS 特性,在被浏览器正式支持之前,浏览器厂商会根据浏览器的内核,使用私有前缀来测试该 CSS 特性,在浏览器正式支持该 CSS 特性后,就不需要私有前缀了。 查询 CSS3 兼容性的网…...
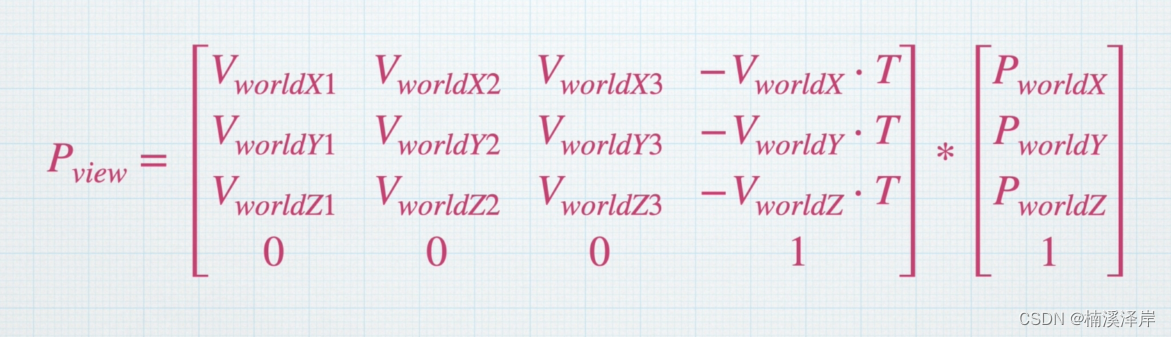
Unity中Shader观察空间推导
文章目录 前言一、本地空间怎么转化到观察空间二、怎么得到观察空间的基向量1、Z轴向量2、假设 观察空间的 Y~假设~ (0,1,0)3、X Y 与 Z 的叉积4、Y X 与 Z 的叉积 三、求 [V~world~]^T^1、求V~world~2、求[V~world~]^T^ 四、求出最后在Unity中使用的公式1、偏移坐标轴2、把…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...
