当前位置： 首页 > news >正文

Unity中Shader观察空间推导

news 2026/2/10 8:02:43

文章目录

  • 前言
  • 一、本地空间怎么转化到观察空间
  • 二、怎么得到观察空间的基向量
    • 1、Z轴向量
    • 2、假设 观察空间的 Y~假设~ = (0,1,0)
    • 3、X = Y 与 Z 的叉积
    • 4、Y = X 与 Z 的叉积
  • 三、求 [V~world~]^T^
    • 1、求V~world~
    • 2、求[V~world~]^T^
  • 四、求出最后在Unity中使用的公式
    • 1、偏移坐标轴
    • 2、把 平移的坐标 构建成之前文章中使用的 平移矩阵
    • 3、化简我们的矩阵

前言

在上一篇文章中，我们推演了矩阵几何计算。

  • Unity中Shader矩阵变换的几何体现

在这篇文章中，我们来推导一下 观察空间（摄像机空间）。

一、本地空间怎么转化到观察空间

可以根据上篇文章的推导得出：

  • 在两个不同角度坐标系下的坐标信息转化可以由如下公式算出。

Pview = [Wview] * Pworld

[Wview] = [Vworld]-1 = [Vworld]T

Pview = [Vworld]T * Pworld

  • Pview顶点在观察空间下的坐标
  • Pworld顶点在世界空间下的坐标
  • Wview世界空间的基向量 在 观察空间下的矩阵
  • Vworld观察空间的基向量 在 世界空间下的矩阵

二、怎么得到观察空间的基向量

  • 我们的观察空间使用的是右手坐标系
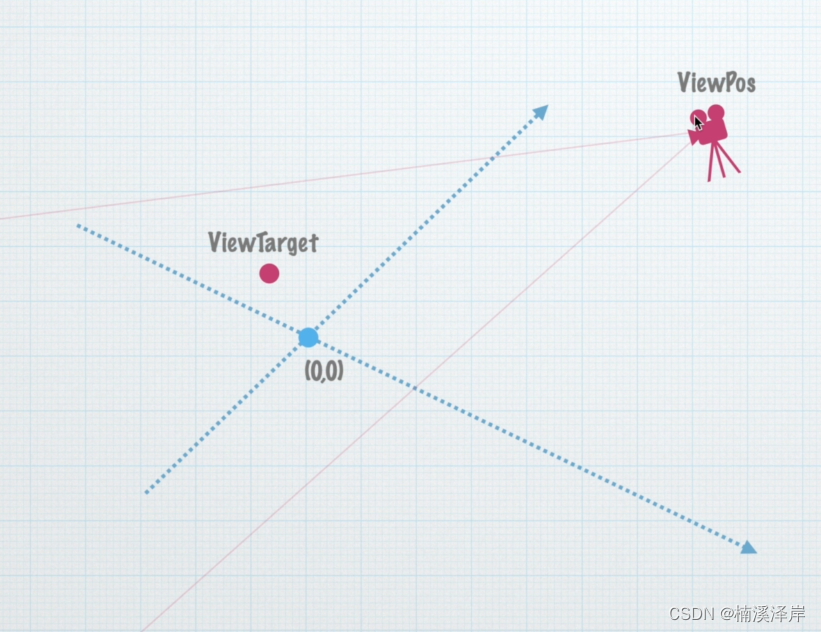
    在这里插入图片描述

在这里插入图片描述

1、Z轴向量

  • Z轴正方向是从 模型顶点 指向 摄像机 方向
  • Z = ViewPos - ViewTarget
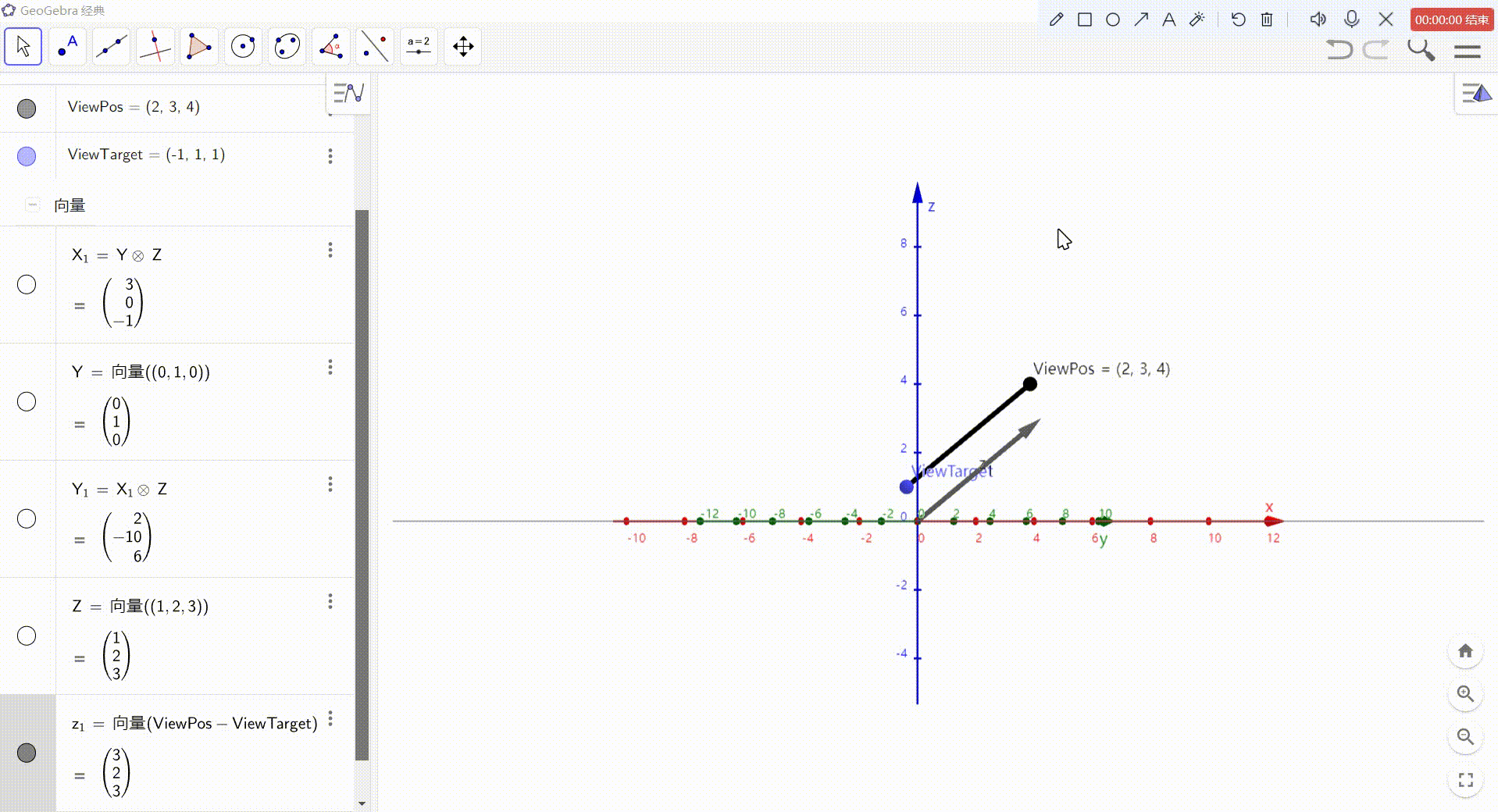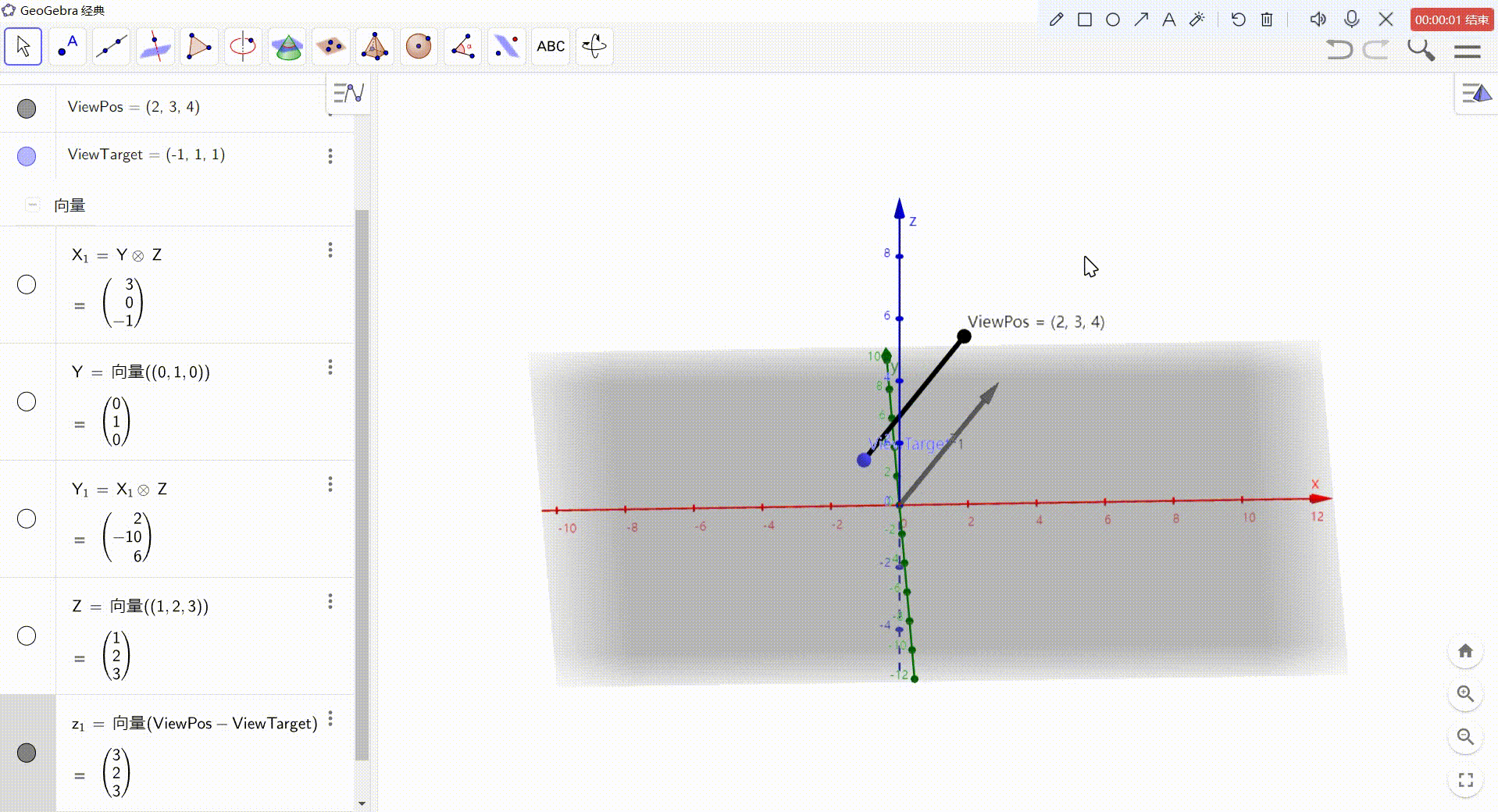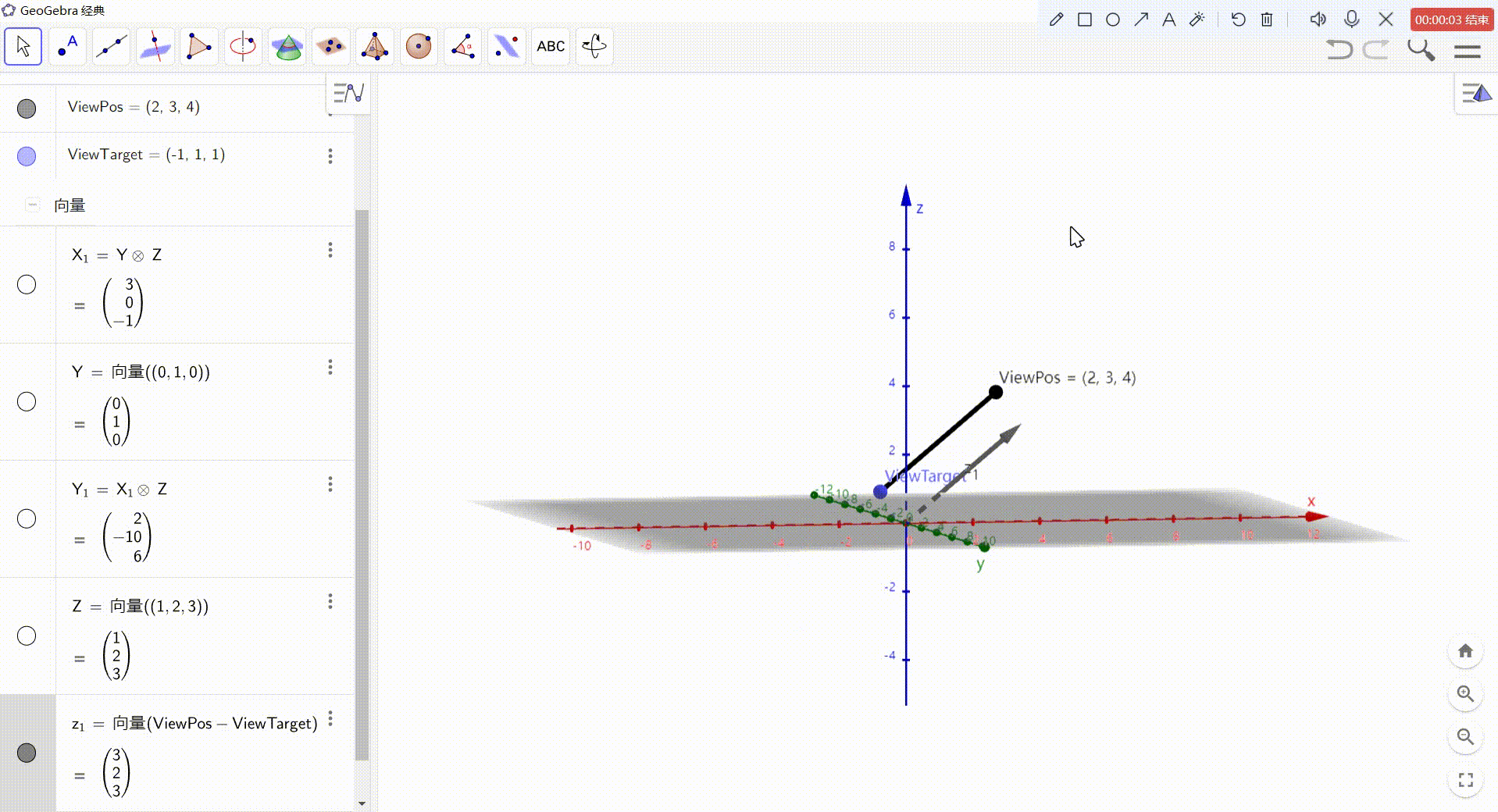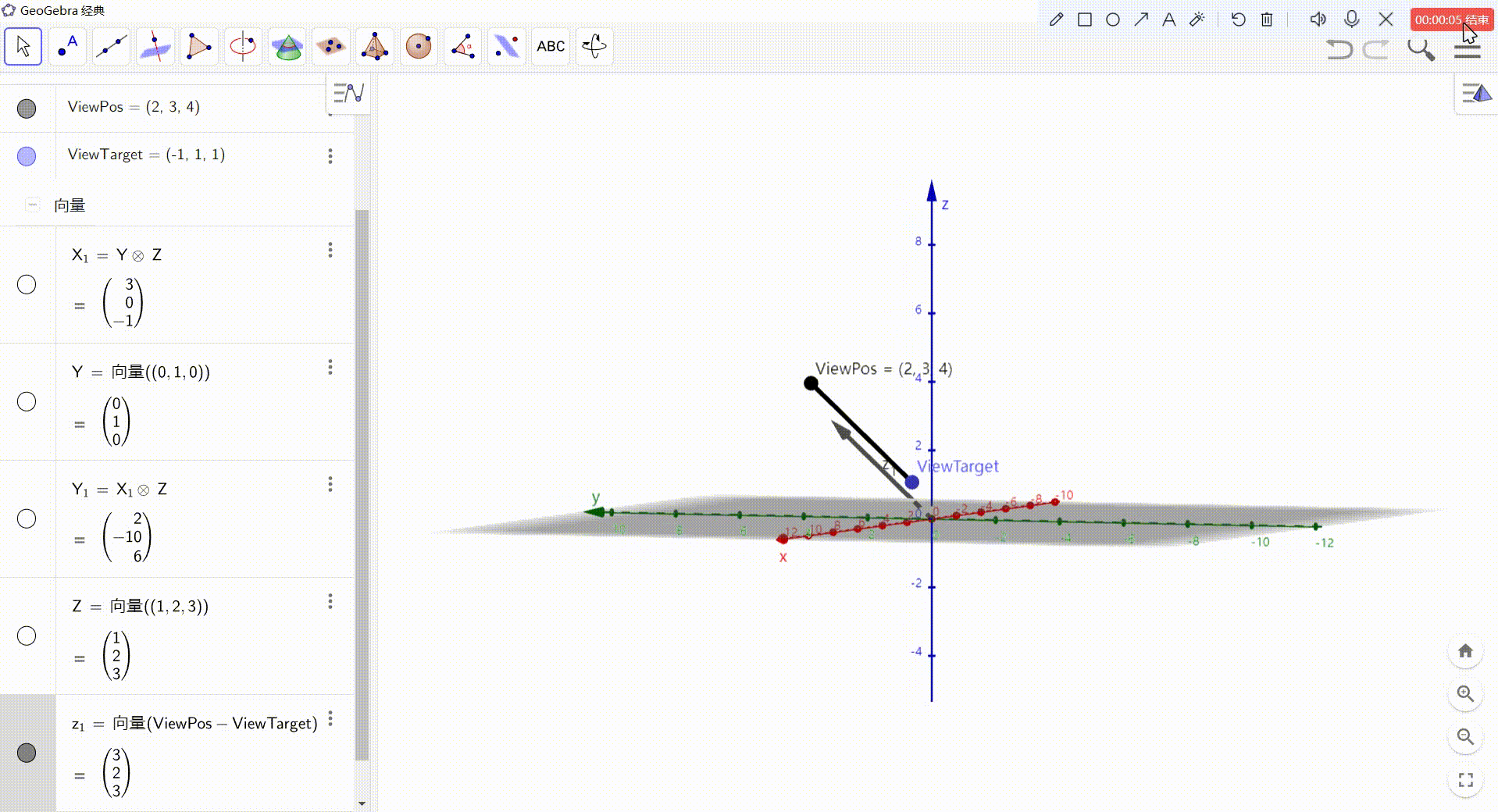
    请添加图片描述
    现在只知道 Z轴，还需要求 X Y轴。

2、假设 观察空间的 Y假设 = (0,1,0)

  • X = Y 与 Z 的叉积
  • Y = X 与 Z 的叉积

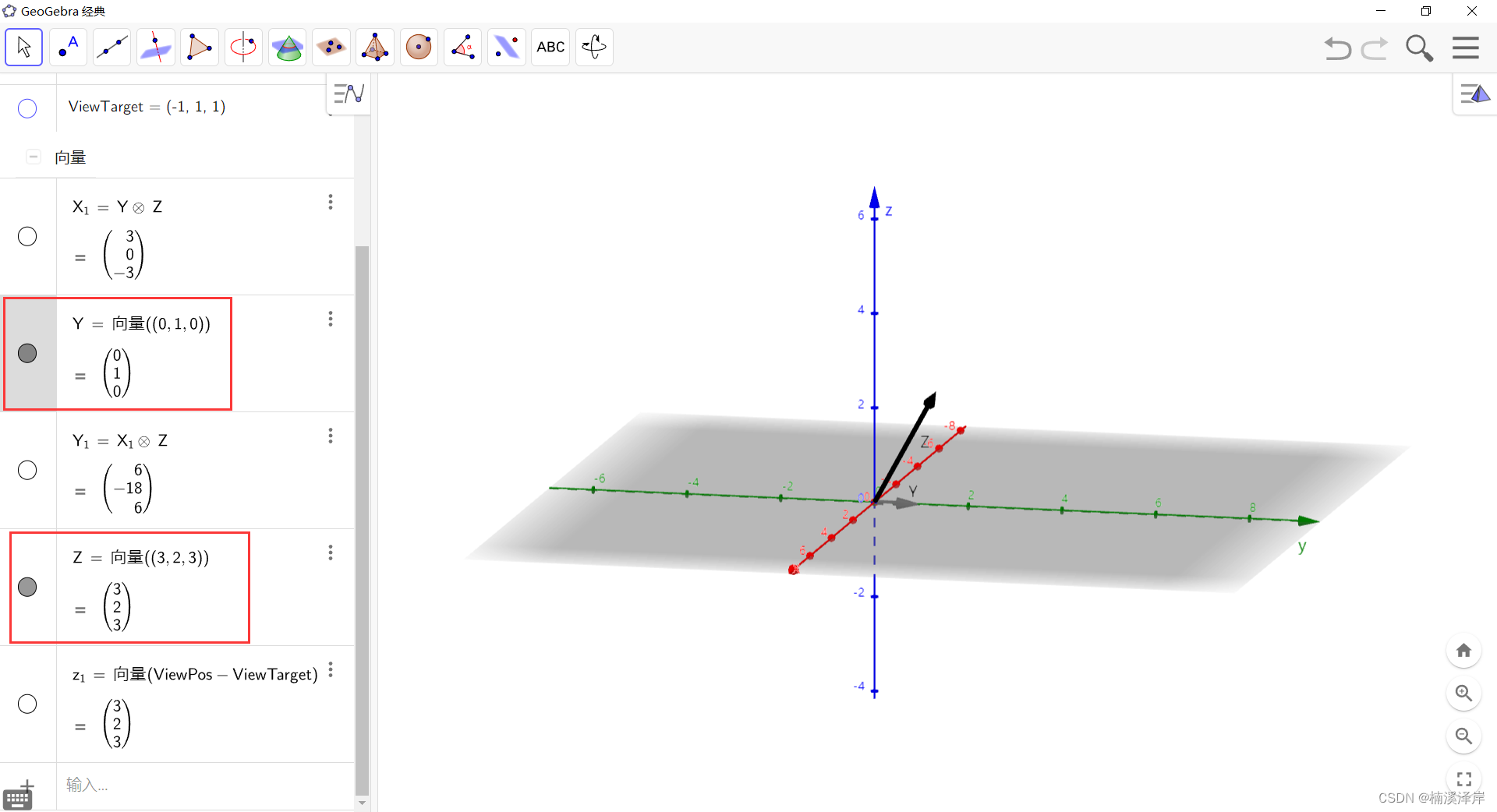
在这里插入图片描述

3、X = Y 与 Z 的叉积

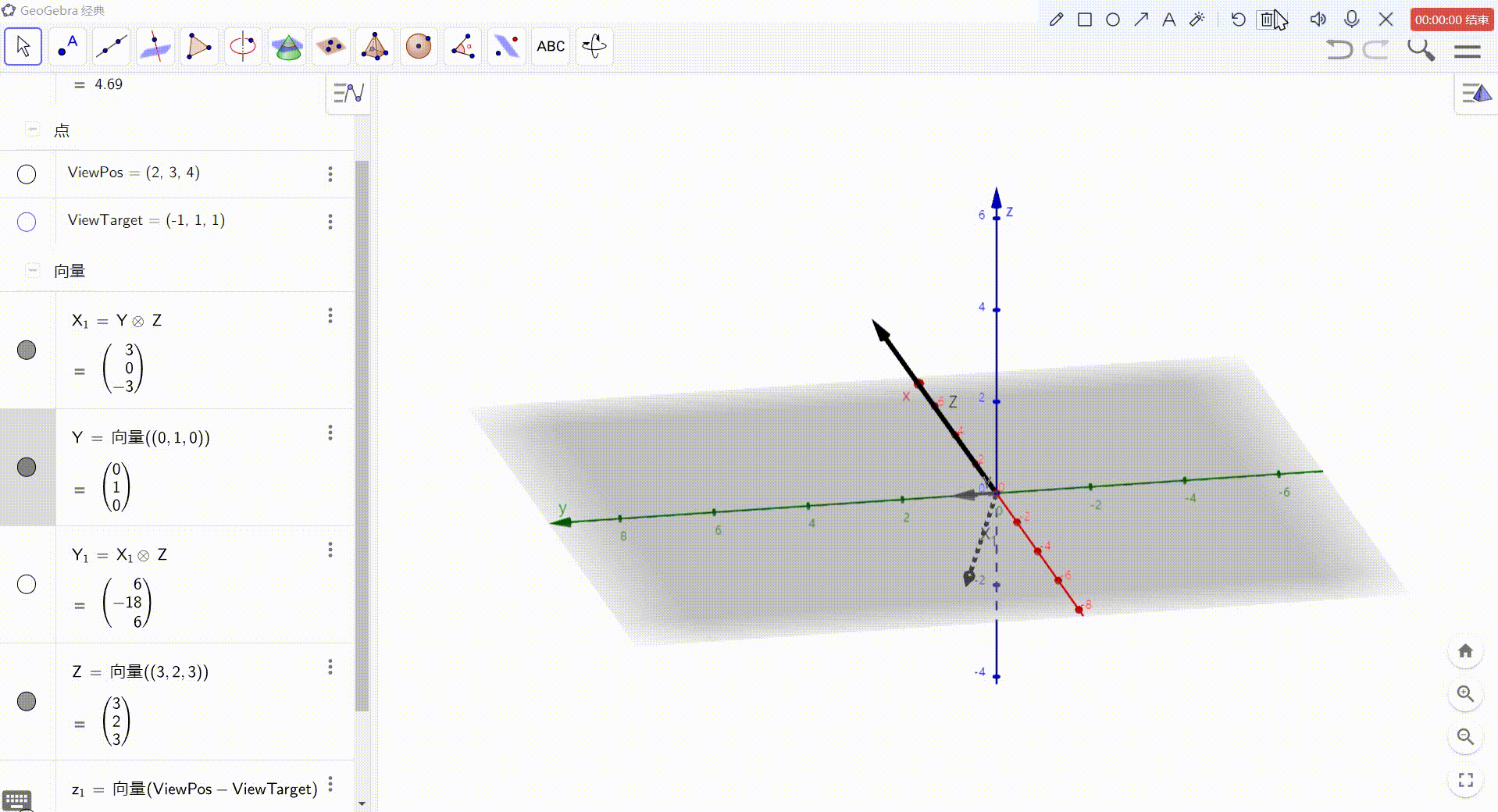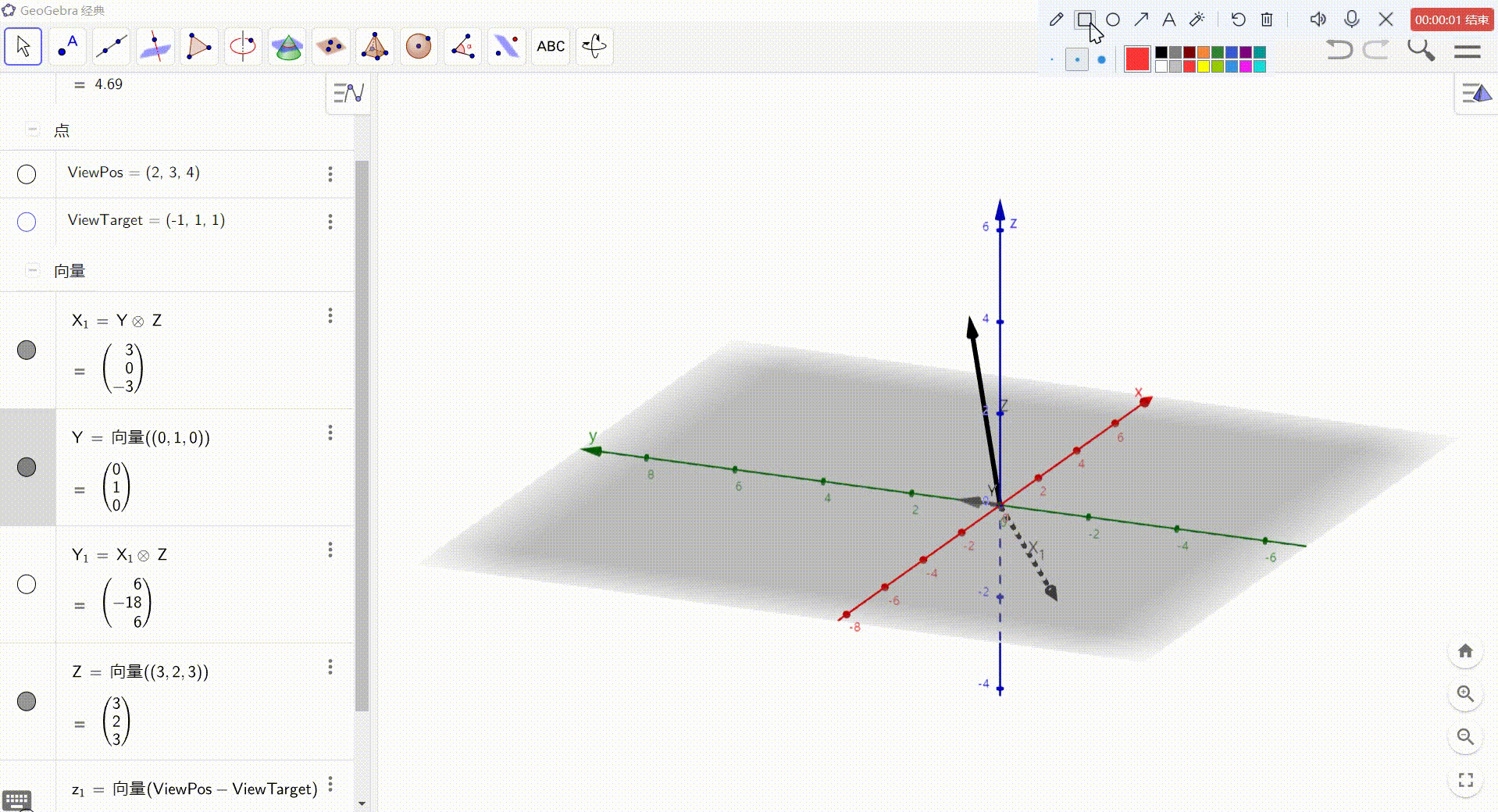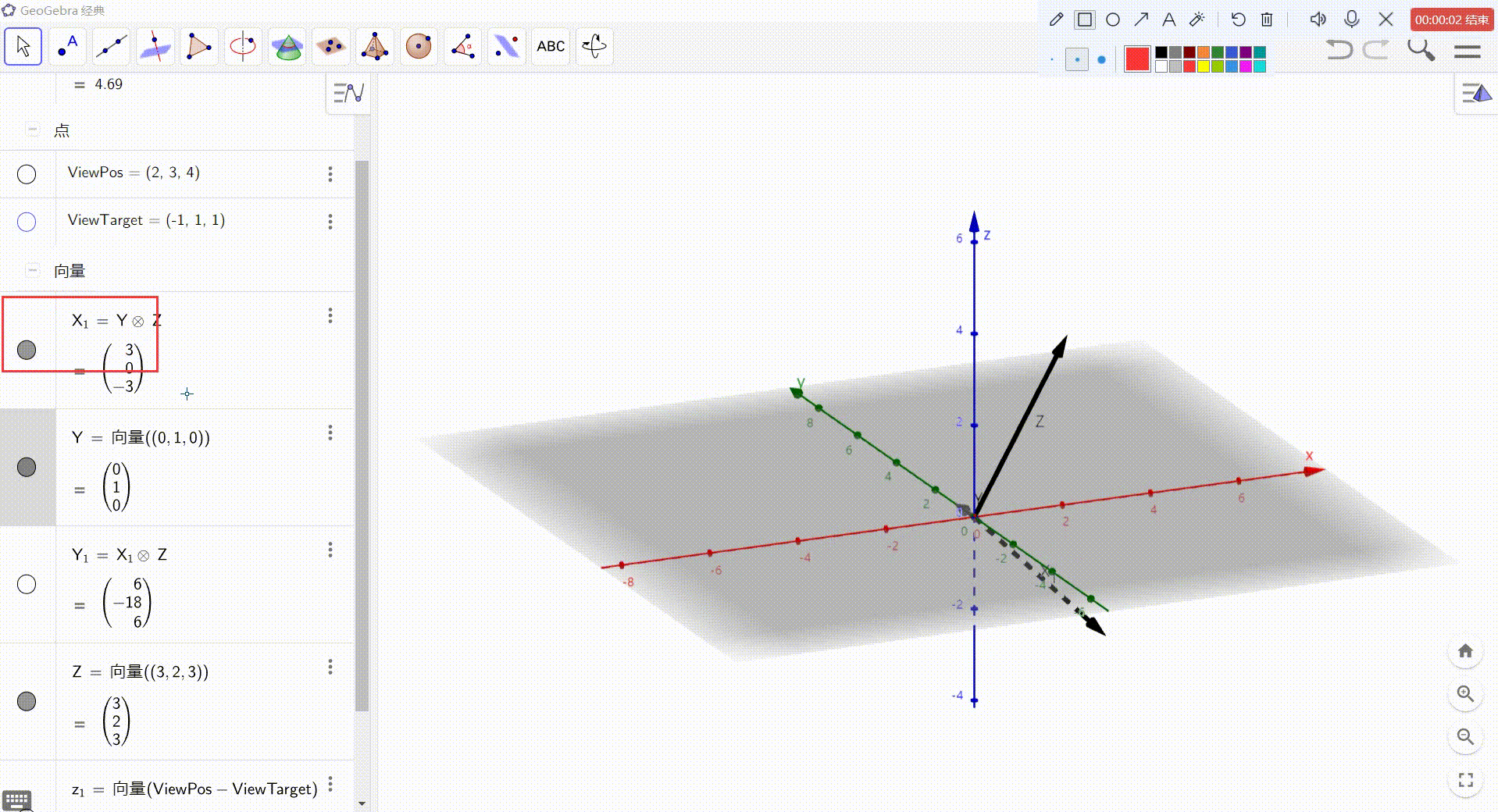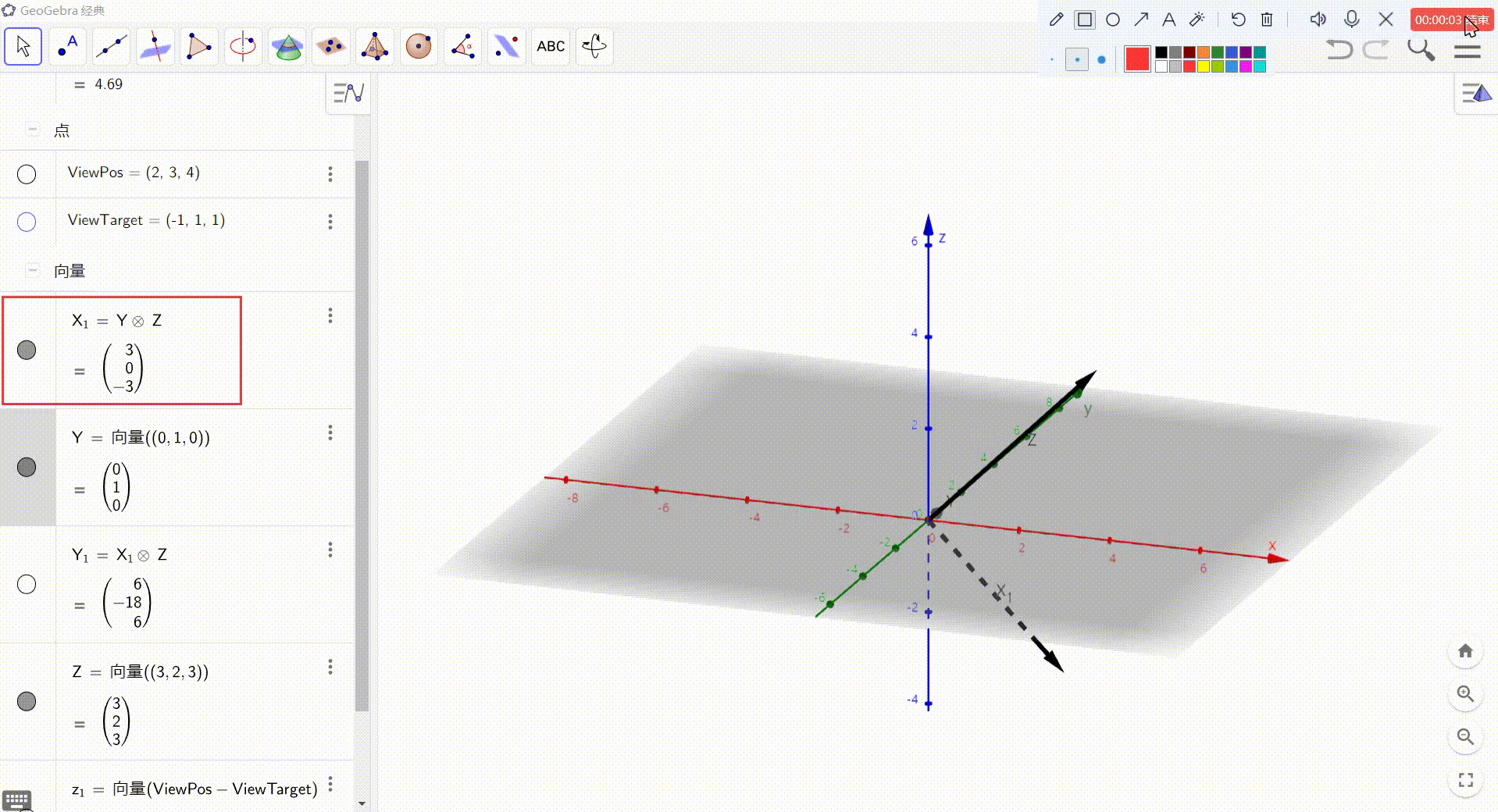
请添加图片描述

4、Y = X 与 Z 的叉积

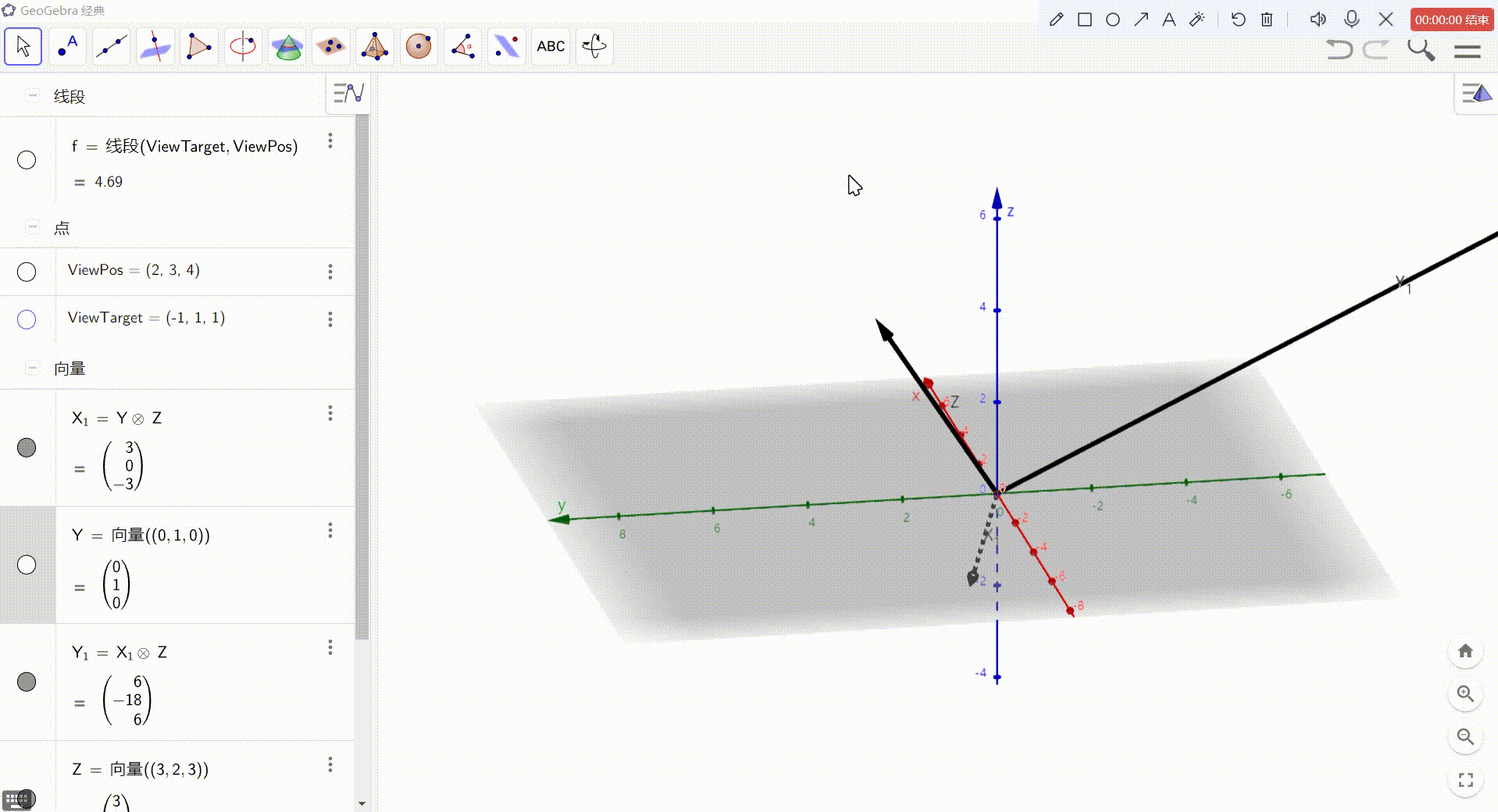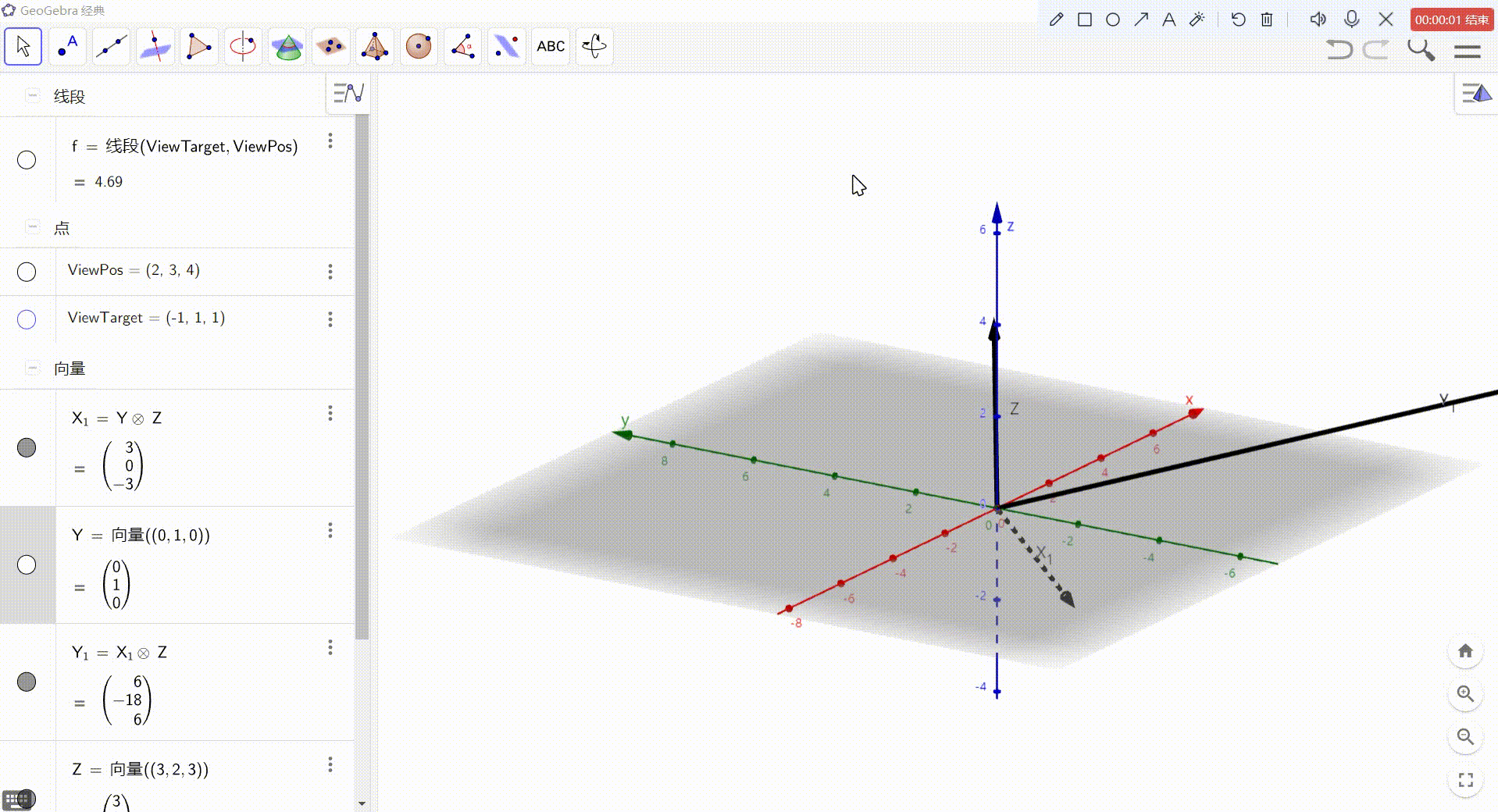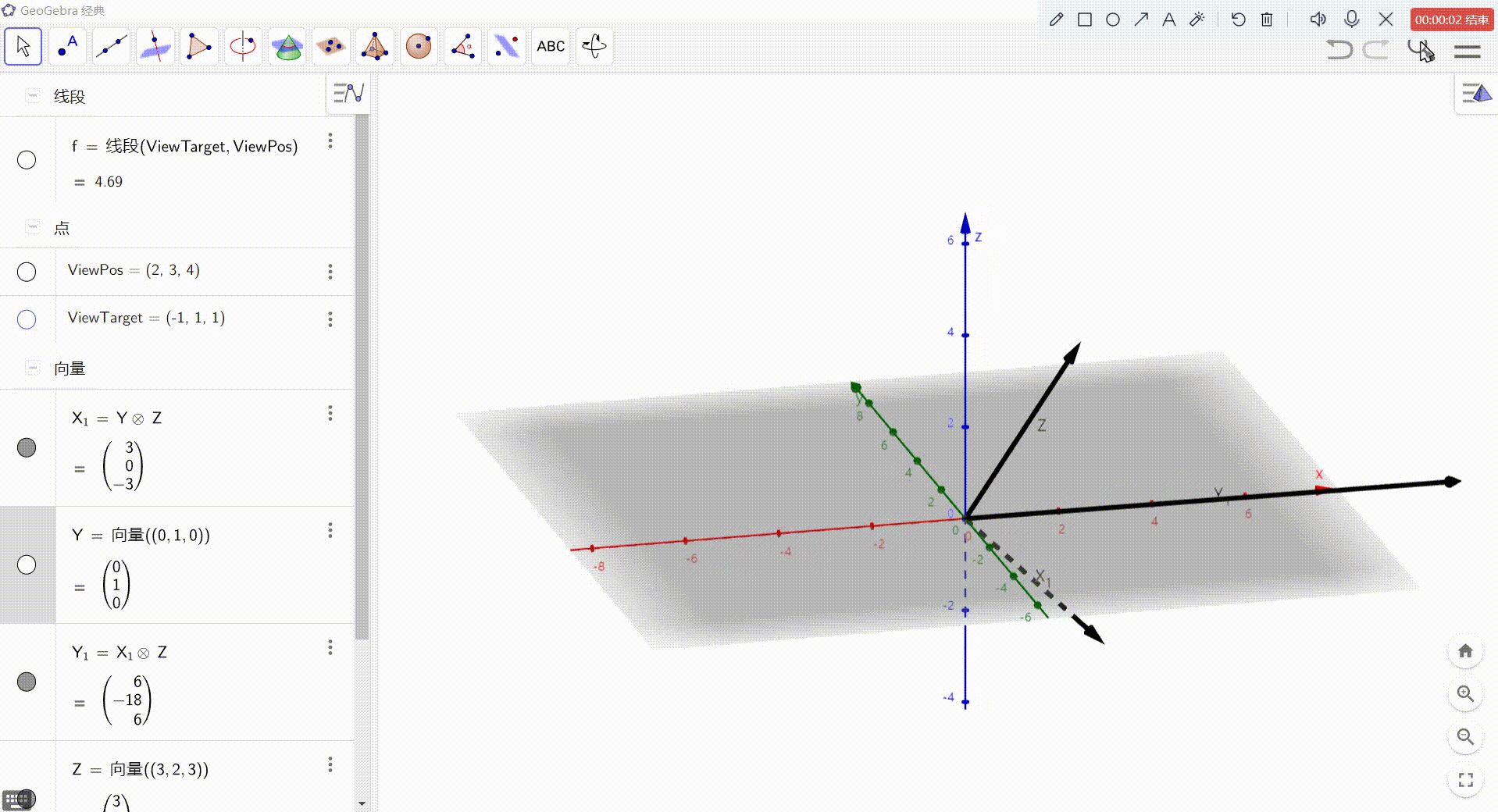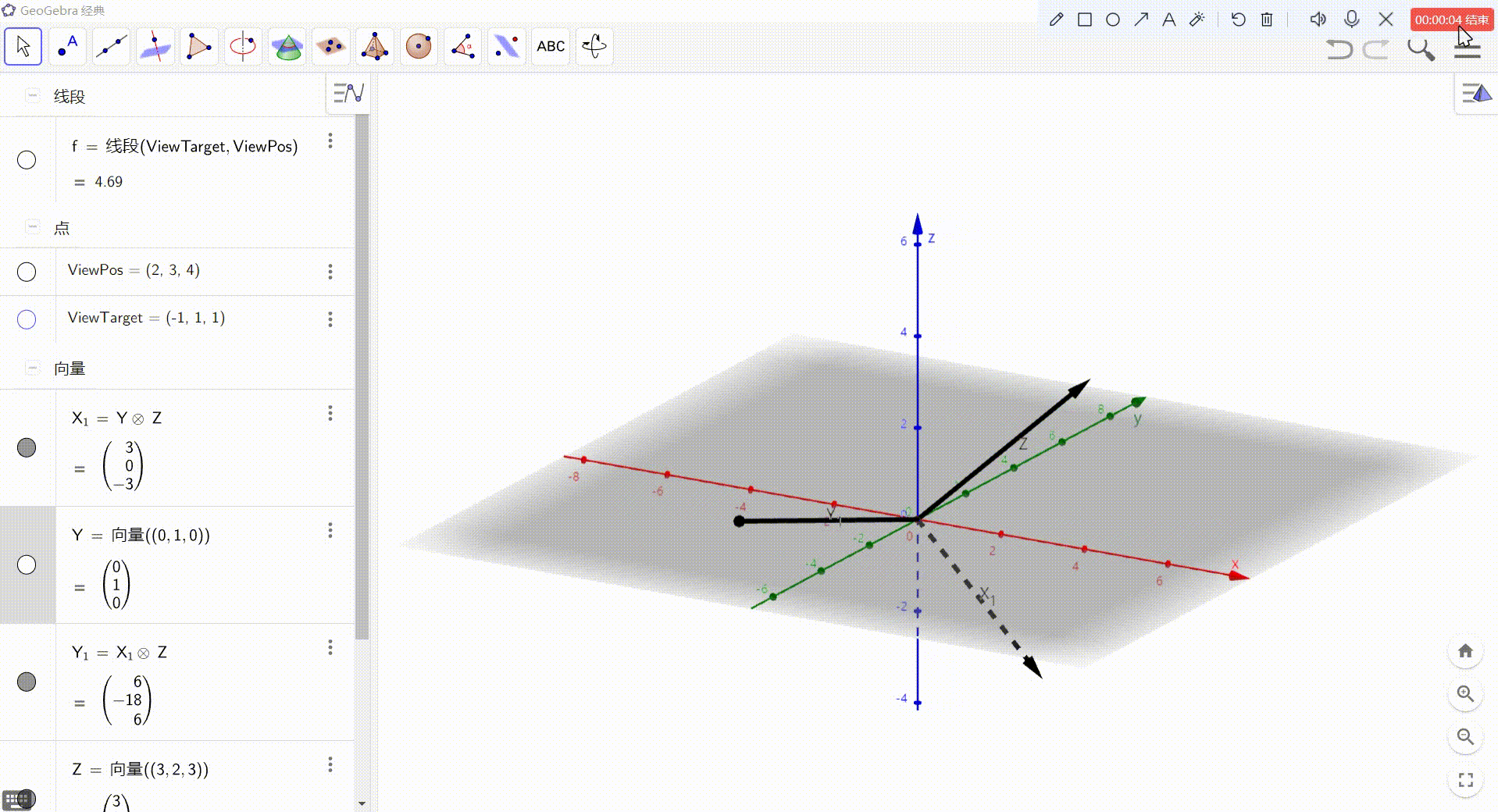
请添加图片描述
最后，得到的就是 视图空间坐标轴方向上的向量，归一化后即可作为基向量使用

三、求 [Vworld]T

1、求Vworld

  • 把基向量一列一列的写来排列得到 Vworld

V w o r l d X x V w o r l d Y x V w o r l d Z x V w o r l d X y V w o r l d Y y V w o r l d Z y V w o r l d X z V w o r l d Y z V w o r l d Z z \begin{matrix} V~worldXx~&V~worldYx~&V~worldZx~\\ V~worldXy~&V~worldYy~&V~worldZy~\\ V~worldXz~&V~worldYz~&V~worldZz~\\ \end{matrix} V worldXx V worldXy V worldXz ​V worldYx V worldYy V worldYz ​V worldZx V worldZy V worldZz ​

2、求[Vworld]T

这里原本是求逆矩阵，但是基向量矩阵是正交矩阵,所以逆矩阵 = 转置矩阵

V w o r l d X x V w o r l d X y V w o r l d X z V w o r l d Y x V w o r l d Y y V w o r l d Y z V w o r l d Z x V w o r l d Z y V w o r l d Z z \begin{matrix} V~worldXx~&V~worldXy~&V~worldXz~\\ V~worldYx~&V~worldYy~&V~worldYz~\\ V~worldZx~&V~worldZy~&V~worldZz~\\ \end{matrix} V worldXx V worldYx V worldZx ​V worldXy V worldYy V worldZy ​V worldXz V worldYz V worldZz ​

四、求出最后在Unity中使用的公式

  • Pview = [Vworld]T * Pworld

1、偏移坐标轴

在之前的步骤中，我们只完成坐标系的旋转转化。
但是，我们的 观察空间 和 世界空间 的原点不在同一地方。
所以，需要进行平移变换

在这里插入图片描述

2、把 平移的坐标 构建成之前文章中使用的 平移矩阵

1 0 0 − T x 0 1 0 − T y 0 0 1 − T z 0 0 0 1 \begin{matrix} 1&0&0&-T~x~\\ 0&1&0&-T~y~\\ 0&0&1&-T~z~\\ 0&0&0&1\\ \end{matrix} 1000​0100​0010​−T x −T y −T z 1​

  • 则我们的公式会变成如下样子：
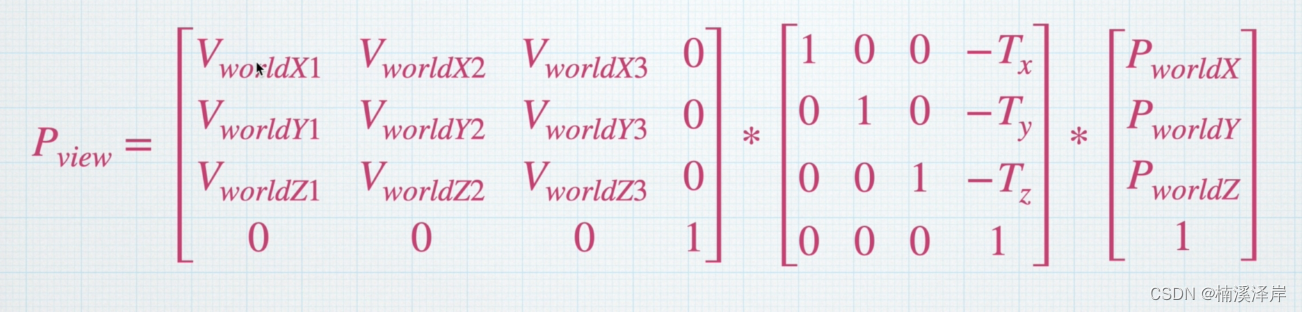
    在这里插入图片描述

3、化简我们的矩阵

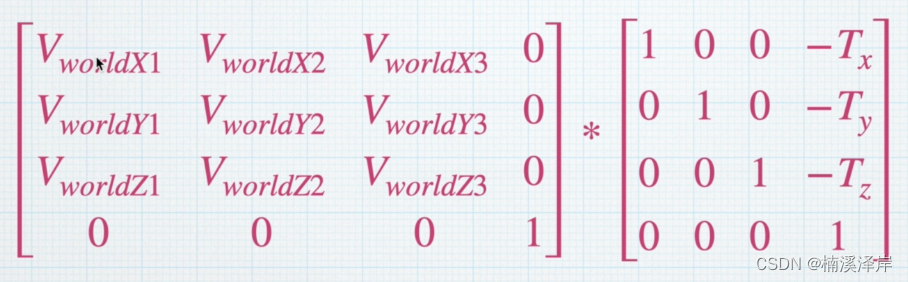
在这里插入图片描述

  • 这两个矩阵相乘，最后的一列的结果，可以化简为：

− ( V w o r l d X d o t T ) − ( V w o r l d Y d o t T ) − ( V w o r l d Z d o t T ) 1 \begin{matrix} -(V~worldX~ dot T) \\ -(V~worldY~ dot T) \\ -(V~worldZ~ dot T) \\ 1\\ \end{matrix} −(V worldX dotT)−(V worldY dotT)−(V worldZ dotT)1​

  • 最后，公式化简为：
    在这里插入图片描述

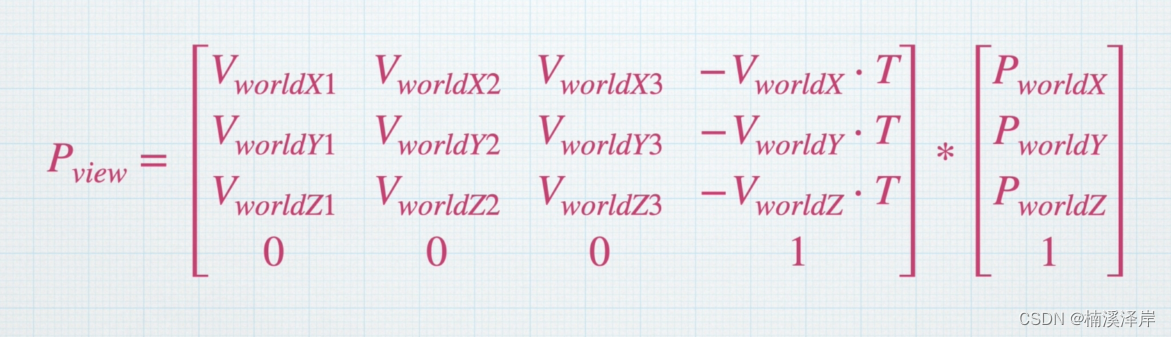
相关文章：

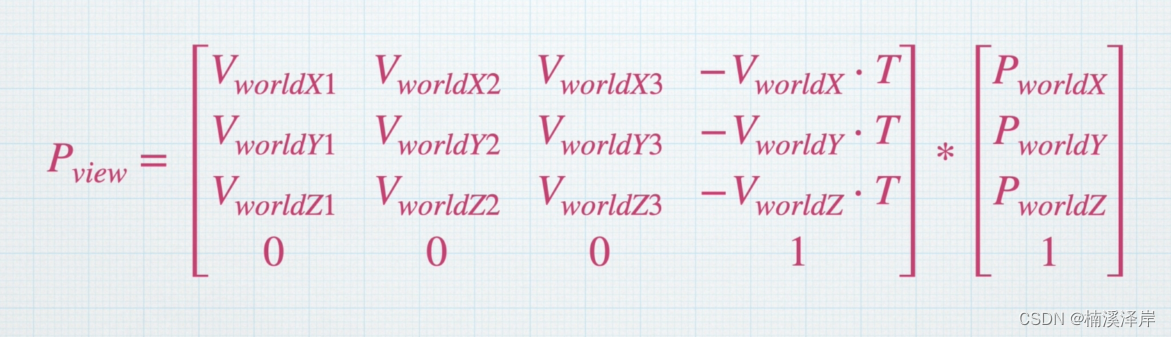
Unity中Shader观察空间推导

文章目录 前言一、本地空间怎么转化到观察空间二、怎么得到观察空间的基向量1、Z轴向量2、假设 观察空间的 Y~假设~ (0,1,0)3、X Y 与 Z 的叉积4、Y X 与 Z 的叉积 三、求 [V~world~]^T^1、求V~world~2、求[V~world~]^T^ 四、求出最后在Unity中使用的公式1、偏移坐标轴2、把…...

编程日记 2023/12/24 12:11:12

信息学奥赛一本通2034：【例5.1】反序输出

2034：【例5.1】反序输出 时间限制: 1000 ms 内存限制: 65536 KB 提交数: 79280 通过数: 35643 【题目描述】 输入nn个数,要求程序按输入时的逆序把这nn个数打印出来，已知整数不超过100100个。也就是说，按输入相反顺序打印这nn个…...

编程日记 2023/12/24 12:10:11

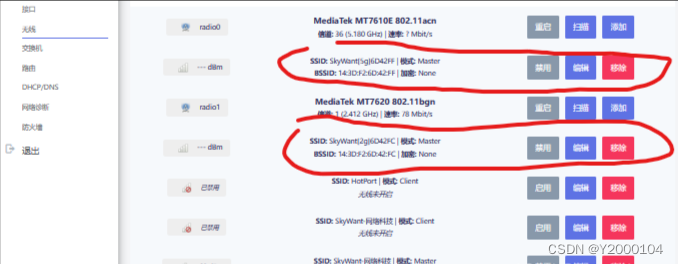
使用教程之【SkyWant.[2304]】路由器操作系统，破解移动【Netkeeper】校园网【小白篇】

许多高校目前饱受Netkeeper认证的痛苦，普通路由器无法使用， 教你利用SkyWant的Netkeeper认证软件来使你的SkyWant路由器顺利认证上网，全宿舍又可以合作共赢了！ 步骤一：正确连接网线，插电开机 正确连接网…...

编程日记 2023/12/24 12:09:10

模式识别与机器学习（十）：梯度提升树

1.原理 提升方法实际采用加法模型（即基函数的线性组合）与前向分步算法。以决策树为基函数的提升方法称为提升树（boosting tree）。对分类问题决策树是二叉分类树，对回归问题决策树是二叉回归树。提升树模型可以表示为决…...

编程日记 2023/12/24 12:08:09

《剑指offer》Java版--12.矩阵中的路径（DFS+剪枝）

剑指offer原题:矩阵中的路径 请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格，那么该路径不能再…...

编程日记 2023/12/24 12:07:07

AI智能体的介绍

最近几个月 随着大语言模型的持续火爆 利用大模型来构建AI智能体的研究呢 也陆续进入了人们的视野 AI智能体这个概念呢 也逐渐的流行开来 先是斯坦福大学谷歌的研究者们 成功的构建了一个虚拟小镇 小镇上的居民呢不再是人 而是25个AI的智能体 他们的行为呢 比人类角…...

编程日记 2023/12/24 12:06:06

Java设计模式-单例模式（Singleton）

Java中实现单例模式有几种不同的方式，每种方式都有其特点和适用场景。下面是两种常用的实现方式：懒汉式和饿汉式。 懒汉式（线程安全） 懒汉式单例是指在第一次被引用时才会创建实例。为了确保线程安全，可以使用同步方法或同步块。 public class SingletonLazy {private sta…...

编程日记 2023/12/24 12:00:02

若依vue如何展示一个HTML页面(或者展示Markdown文档)

一. 前言 ⚠ 本文是展示Markdown的方法,不能直接前端编辑Markdown文档. 二. 准备部分 用Typora编辑器打开需要导出html页面,我这里使用Typora来导出 1. 先将md文件导出成html 2. 将导出好的文件放在若依vue的pubilc下(文件可以是中文) 三. 代码部分 1.使用v-html来展示HT…...

编程日记 2023/12/24 11:59:00

优化for循环（js的问题）

性能优化 var array [];for (let index 0; index < array.length; index) {// do something }// 优化后 for (let index 0, len array.length; index < len; index) {// do something } 算法优化 // 求和&#xff1a;1 2 3 4 ... 100 var sum 0; for (let i …...

编程日记 2023/12/24 11:54:57

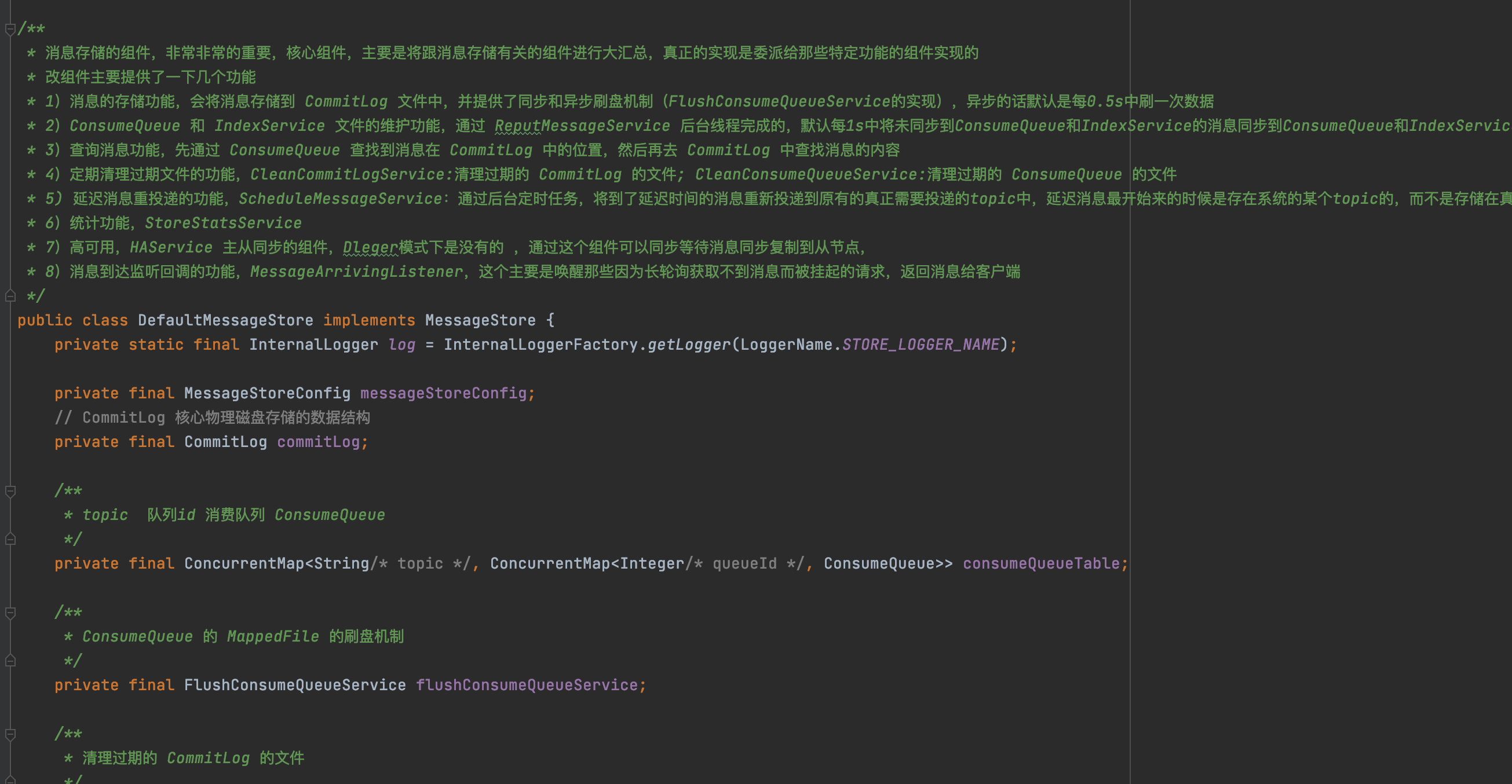
如何更好的去理解源码

前言 这篇文章我准备来聊一聊如何去阅读开源项目的源码。 在聊如何去阅读源码之前&#xff0c;先来简单说一下为什么要去阅读源码&#xff0c;大致可分为以下几点原因&#xff1a; 最直接的原因&#xff0c;就是面试需要&#xff0c;面试喜欢问源码&#xff0c;读完源码才可以…...

编程日记 2023/12/24 11:53:56

c# opencv 获取多边形中心点

在C#中使用OpenCV获取多边形的中心点&#xff0c;可以按照以下步骤进行&#xff1a; 首先&#xff0c;你需要找到图像中的轮廓。这可以通过FindContours方法实现&#xff1a; using OpenCvSharp;Mat src new Mat("your_image_path", ImreadModes.Grayscale); Mat …...

编程日记 2023/12/24 11:51:54

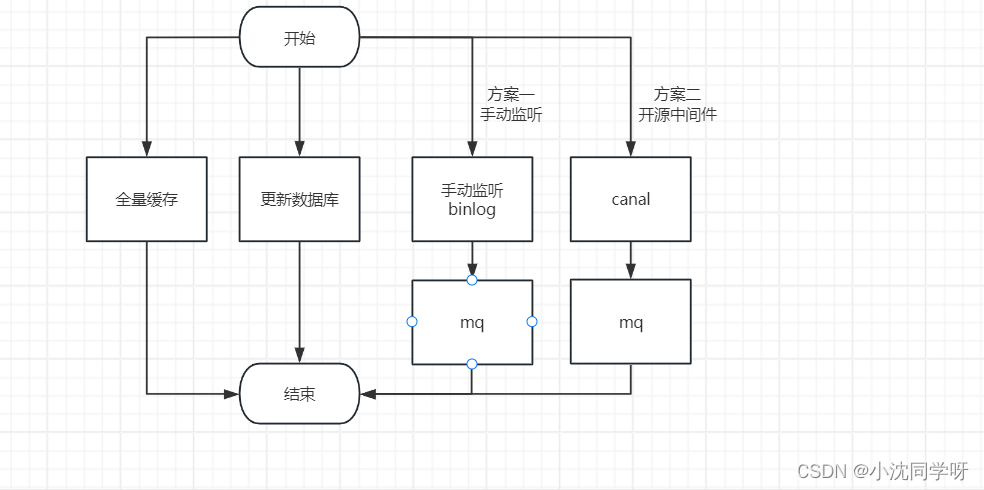
Redis数据一致解决方案

文章目录 前言技术积累查询缓存业务流程更新缓存业务流程 更新缓存问题解决方案写在最后 前言 当前的应用服务很多都有着高并发的业务场景&#xff0c;对于高并发的解决方案一般会用到缓存来降低数据库压力&#xff0c;并且还能够提高系统性能减少请求耗时&#xff0c;比如我们…...

编程日记 2023/12/24 11:49:52

安捷伦DSOX2024A示波器

参考波形 示波器的非易失参考波形存储器可以存储两个波形。比较这些参考波形与实时波形&#xff0c;并对已存储数据进行后分析和测量。您也可将波形数据存储到移动USB 存储器设备。这些数据还能调用到示波器的两个参考存储器的其中一个&#xff0c;进行全面的波形测量和分析。为…...

编程日记 2023/12/24 11:48:51

Leetcode算法系列| 4. 寻找两个正序数组的中位数

目录 1.题目2.题解C# 解法一&#xff1a;合并List根据长度找中位数C# 解法二&#xff1a;归并排序后根据长度找中位数C# 解法三&#xff1a;方法二的优化&#xff0c;不真实添加到listC# 解法四&#xff1a;第k小数C# 解法五&#xff1a;从中位数的概念定义入手 1.题目 给定两个…...

编程日记 2023/12/24 11:44:47

Java整合APNS推送消息-IOS-APP（基于.p12推送证书）

推送整体流程 1.在开发者中心申请对应的证书&#xff08;我用的是.p12文件&#xff09; 2.苹果手机用户注册到APNS&#xff0c;APNS将注册的token返回给APP&#xff08;服务端接收使用&#xff09;。 3.后台服务连接APNS&#xff0c;获取连接对象 4.后台服务构建消息载体 5.后台…...

编程日记 2023/12/24 11:41:44

C语言strcpy函数用法

C语言strcpy函数用法 大家好&#xff0c;我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编&#xff0c;也是冬天不穿秋裤&#xff0c;天冷也要风度的程序猿&#xff01;今天&#xff0c;让我们一起深入了解C语言中的strcpy函数&#xff0c;这是一个在字符串处理中非…...

编程日记 2023/12/24 11:38:42

汽车服务品牌网站建设的作用是什么

汽车服务涵盖多个层面&#xff0c;在保修维护这一块更是精准到了车内车外&#xff0c;无论是品牌商还是市场中各维修部&#xff0c;都能给到车辆很好的维修养护服务。如今车辆的人均拥有量已经非常高&#xff0c;也因此市场中围绕汽车相关的从业者也比较多。 首先就是拓客引流…...

编程日记 2023/12/24 11:30:35

【iOS】UICollectionView

文章目录 前言一、实现简单九宫格布局二、UICollectionView中的常用方法和属性1.UICollectionViewFlowLayout相关属性2.UICollectionView相关属性 三、协议和代理方法&#xff1a;四、九宫格式的布局进行升级五、实现瀑布流布局实现思路实现原理代码调用顺序实现步骤实现效果 总…...

编程日记 2023/12/24 11:25:25

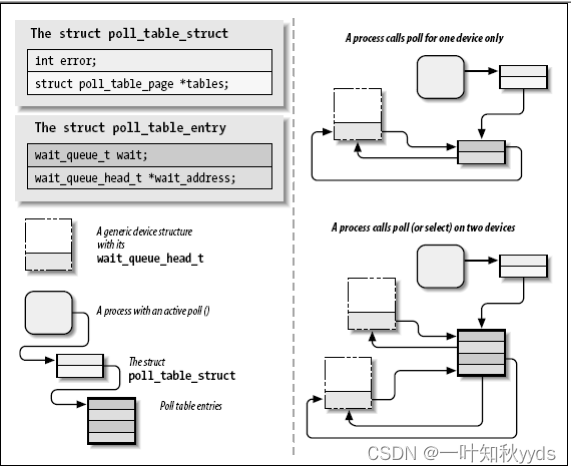
Linux poll 和 select 机制

poll select 介绍 使用非阻塞 I/O 的应用程序常常使用 poll, select, 和 epoll 系统调用. poll, select 和 epoll 本质上有相同的功能: 每个允许一个进程来决定它是否可读或者写一个 或多个文件而不阻塞. 这些调用也可阻塞进程直到任何一个给定集合的文件描述符可用来 读或写.…...

编程日记 2023/12/24 11:18:20

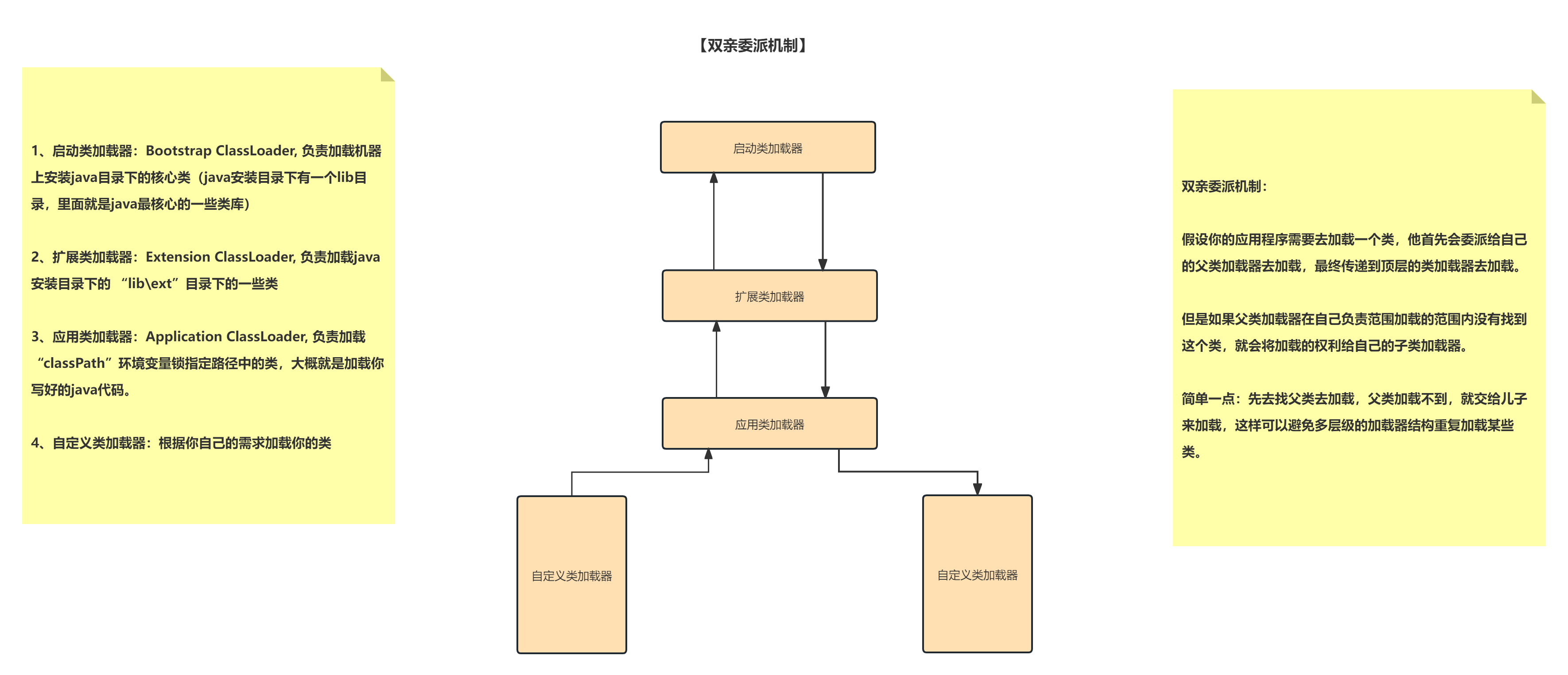
【JVM基础】 JVM 如何加载一个类以及类加载机制

文章目录 1、什么时候一个类会被加载&#xff1f;1、包含 main 方法的主类2、非 包含 main 方法的主类&#xff0c;什么时候去加载&#xff1f; 3、类加载器如何加载一个类&#xff1f;1、验证阶段&#xff1a;2、准备阶段&#xff1a;3、解析阶段&#xff1a;4、初始化&#x…...

编程日记 2023/12/24 11:15:16

conda相比python好处

Conda 作为 Python 的环境和包管理工具&#xff0c;相比原生 Python 生态&#xff08;如 pip 虚拟环境&#xff09;有许多独特优势&#xff0c;尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处&#xff1a; 一、一站式环境管理&#xff1a…...

编程新知 2025/11/29 6:54:19

Linux简单的操作

ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

编程新知 2026/1/20 14:36:39

生成 Git SSH 证书

&#x1f511; 1. ​​生成 SSH 密钥对​​ 在终端&#xff08;Windows 使用 Git Bash&#xff0c;Mac/Linux 使用 Terminal&#xff09;执行命令&#xff1a; ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" ​​参数说明​​&#xff1a; -t rsa&#x…...

编程新知 2025/9/18 11:31:13

如何将联系人从 iPhone 转移到 Android

从 iPhone 换到 Android 手机时&#xff0c;你可能需要保留重要的数据&#xff0c;例如通讯录。好在&#xff0c;将通讯录从 iPhone 转移到 Android 手机非常简单&#xff0c;你可以从本文中学习 6 种可靠的方法&#xff0c;确保随时保持连接&#xff0c;不错过任何信息。 第 1…...

编程新知 2026/1/31 5:09:27

使用LangGraph和LangSmith构建多智能体人工智能系统

现在&#xff0c;通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战&#xff0c;比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

编程新知 2026/1/26 13:48:59

iview框架主题色的应用

1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题&#xff0c;无需引入&#xff0c;直接可…...

编程新知 2026/1/31 9:29:45

第7篇：中间件全链路监控与 SQL 性能分析实践

7.1 章节导读 在构建数据库中间件的过程中&#xff0c;可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中&#xff0c;必须做到&#xff1a; &#x1f50d; 追踪每一条 SQL 的生命周期&#xff08;从入口到数据库执行&#xff09;&#…...

编程新知 2025/12/11 0:27:15

通过MicroSip配置自己的freeswitch服务器进行调试记录

之前用docker安装的freeswitch的&#xff0c;启动是正常的&#xff0c; 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

编程新知 2026/2/6 14:23:05

软件工程 期末复习

瀑布模型&#xff1a;计划 螺旋模型&#xff1a;风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合&#xff1a;模块内部功能紧密 模块之间依赖程度小 高内聚&#xff1a;指的是一个模块内部的功能应该紧密相关。换句话说&#xff0c;一个模块应当只实现单一的功能…...

编程新知 2026/2/10 0:32:51

【Kafka】Kafka从入门到实战：构建高吞吐量分布式消息系统

Kafka从入门到实战：构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台，最初由LinkedIn开发，后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理，能够处理来自多个生产者的海量数据，并将这些数据实时传递给消费者。 Kafka核心特…...

编程新知 2025/7/18 7:59:36