Leetcode算法系列| 4. 寻找两个正序数组的中位数
目录
- 1.题目
- 2.题解
- C# 解法一:合并List根据长度找中位数
- C# 解法二:归并排序后根据长度找中位数
- C# 解法三:方法二的优化,不真实添加到list
- C# 解法四:第k小数
- C# 解法五:从中位数的概念定义入手
1.题目
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
- 示例1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
- 示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
- 提示:
- nums1.length == m
- snums2.length == n
- 0 <= m <= 1000
- 0 <= n <= 1000
- 1 <= m + n <= 2000
- -10^6 <= nums1[i], nums2[i] <= 10^6
2.题解
C# 解法一:合并List根据长度找中位数
- 提new 一个 List , 并将 nums1 和 nums2 都添加到list 中,然后进行排序。对于排序后的 list, 根据长度计算出中位数的index,进而计算出最终结果。假设合并后的list长度为13,则从小到大第7个数字为中位数,resultIndex=6;假设合并后的list长度为14,则从小到大第7,8个数字的平均值为中位数,index 分别为 6,7,此时resultIndex =7,resultIndex-1 =6 , 结果为 ( list[resultIndex-1] + list[resultIndex] ) / 2.0 ;
public class Solution {public double FindMedianSortedArrays(int[] nums1, int[] nums2){int m = nums1.Length;int n = nums2.Length;int len = m + n;var resultIndex = len / 2;List<int> list = new List<int>(nums1);list.AddRange(nums2);list.Sort();if (len % 2 == 0){return (list[resultIndex - 1] + list[resultIndex]) / 2.0;}else{return list[resultIndex];}}
}

- 时间复杂度:O( (m+n)(1+log(m+n) ))
- 将长度为m,n的两个数组添加到list,复杂度分别为常数级的m和n ;list.Sort()的复杂度根据官方文档可得为 (m+n)log(m+n),所以该方法时间复杂度为 O( m+n+(m+n)log(m+n) ) = O( (m+n)(1+log(m+n) ))
- 空间复杂度:O(m+n)
- 使用list的长度为m+n.
C# 解法二:归并排序后根据长度找中位数
- 方法一使用了list.Sort() 方法,可以对list进行排序,但是,若题目给出的nums1 和 nums2 是无序数组,使用 list.Sort() 才算是 物有所用。 本题中 nums1 和 nums2 是有序数组,所以使用 list.Sort() 有写 杀鸡用宰牛刀的感觉,换句话说,这里面存在着效率的浪费。我们可以利用 【nums1 和 nums2 是有序数组】 这个条件,来精简我们的排序。
public class Solution {public double FindMedianSortedArrays(int[] nums1, int[] nums2){// nums1 与 nums2 有序添加到list中List<int> list = new List<int>();int i = 0, j = 0;int m = nums1.Length;int n = nums2.Length;int len = m + n;var resultIndex = len / 2;while (i < m && j < n){if (nums1[i] < nums2[j])list.Add(nums1[i++]);elselist.Add(nums2[j++]);}while (i < m) list.Add(nums1[i++]);while (j < n) list.Add(nums2[j++]);if (len % 2 == 0){return (list[resultIndex - 1] + list[resultIndex]) / 2.0;}else{return list[resultIndex];}}
}

- 时间复杂度:O(m+n)
- i 和 j 一起把长度为 m 和 n 的两个数组遍历了一遍,所以时间复杂度为 O(m+n)
- 空间复杂度:O(m+n)
- 使用list的长度为m+n.
C# 解法三:方法二的优化,不真实添加到list
- 对于方法二,我们在已知 resultIndex 的情况下,也可以不把 nums1 和 nums2 真实添加到 list 中,只需要在i 和 j 不断向右移动的过程中,计算是否到达了 resultIndex 即可。 若到达了 resultIndex,可以直接返回结果,而不必再处理后面的数据。但是相对的,我们需要在 i 或者 j 向右移动时,判断是否到达了resultIndex.
public class Solution {public double FindMedianSortedArrays(int[] nums1, int[] nums2){int i = 0, j = 0, m = nums1.Length, n = nums2.Length;int len = m + n;int resultIndex = len / 2;int resultIndexPre = resultIndex - 1;int result = 0, resultPre = 0; bool isTwoResult = len % 2 == 0;while (i < m || j < n){var nums1ii = i < m ? nums1[i] : int.MaxValue;var nums2jj = j < n ? nums2[j] : int.MaxValue;if (nums1ii < nums2jj){if (i + j == resultIndexPre) resultPre = nums1[i];if (i + j == resultIndex){result = nums1[i];if (isTwoResult) return (resultPre + result) / 2.0;else return result;}i++;}else{if (i + j == resultIndexPre) resultPre = nums2[j];if (i + j == resultIndex){result = nums2[j];if (isTwoResult) return (resultPre + result) / 2.0;else return result;}j++;}}return 0;}
}

- 时间复杂度:O(m+n)
- i 和 j 一起把长度为 m 和 n 的两个数组遍历了一半,但是每一步都需要判断当前i+j的值是否等于resultIndex,所以时间复杂度仍可认为 O(m+n)
- 空间复杂度:O(1)
- 对比方法二,不再使用list,只使用了几个变量来存值,所以空间复杂度为O(1)
C# 解法四:第k小数
- 前面的几种方法,时间复杂度都没有达到题目要求的 O(log(m+n)) 。 看到log,很明显需要使用二分法。根据 windliang提供的思路,题目求中位数,实际上是求第 k 小数的一种特殊情况,而求第 k 小数 有一种算法。
方法三中,i 和 j 每次向右移动一位时,相当于去掉了一个不可能是中位数的值,也就是一个一个的排除。由于给定的两个数组是有序的,所以我们完全可以一半一半的排除。假设我们要找第 k 小数,我们每次循环可以安全的排除掉 k/2 个数。
public class Solution {public double FindMedianSortedArrays(int[] nums1, int[] nums2){int n = nums1.Length;int m = nums2.Length;int len = n + m;int kPre = (len + 1) / 2;int k = (len + 2) / 2;if (len % 2 == 0)return (GetKth(nums1, 0, n - 1, nums2, 0, m - 1, kPre) + GetKth(nums1, 0, n - 1, nums2, 0, m - 1, k)) * 0.5;elsereturn GetKth(nums1, 0, n - 1, nums2, 0, m - 1, k);}private int GetKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k){int len1 = end1 - start1 + 1;int len2 = end2 - start2 + 1;//让 len1 的长度小于 len2,这样就能保证如果有数组空了,一定是 len1 if (len1 > len2) return GetKth(nums2, start2, end2, nums1, start1, end1, k);if (len1 == 0) return nums2[start2 + k - 1];if (k == 1) return Math.Min(nums1[start1], nums2[start2]);int i = start1 + Math.Min(len1, k / 2) - 1;int j = start2 + Math.Min(len2, k / 2) - 1;if (nums1[i] > nums2[j])return GetKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));elsereturn GetKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));}
}

- 时间复杂度:O(log(m+n))
- i每进行依次循环,就减少 k/2个元素,所以时间复杂度为 O(log(k)) , 而 k = (m+n)/2 , 所以最终复杂度是 O(log(m+n))
- 空间复杂度:O(1)
- 只使用了几个变量来存值,递归是尾递归不占用堆栈, 所以空间复杂度为O(1)
C# 解法五:从中位数的概念定义入手
- 该方法参考了 LeetCode 题解的 官方题解 以及 windliang 的题解。
首先我们来看一下百度百科中位数的定义:https://baike.baidu.com/item/%E4%B8%AD%E4%BD%8D%E6%95%B0/3087401?fr=aladdin
public class Solution {public double FindMedianSortedArrays(int[] A, int[] B){int m = A.Length;int n = B.Length;//保证第一个数组是较短的if (m > n) return FindMedianSortedArrays(B, A);//正在寻找的范围为 [ A[iMin],A[iMax] ) , 左闭右开。二分查找取i=(iMin+iMax)/2int iMin = 0, iMax = m;while (iMin <= iMax){int i = (iMin + iMax) / 2;int j = (m + n + 1) / 2 - i;if (j != 0 && i != m && B[j - 1] > A[i]){ // i 需要增大iMin = i + 1;}else if (i != 0 && j != n && A[i - 1] > B[j]){ // i 需要减小iMax = i - 1;}else{ // 达到要求,并且将边界条件列出来单独考虑int maxLeft = 0;if (i == 0) { maxLeft = B[j - 1]; }else if (j == 0) { maxLeft = A[i - 1]; }else { maxLeft = Math.Max(A[i - 1], B[j - 1]); }if ((m + n) % 2 == 1) { return maxLeft; } // 奇数的话不需要考虑右半部分int minRight = 0;if (i == m) { minRight = B[j]; }else if (j == n) { minRight = A[i]; }else { minRight = Math.Min(B[j], A[i]); }return (maxLeft + minRight) / 2.0; //如果是偶数的话返回结果}}return 0.0;}
}

- 时间复杂度:O(log(min(m,n))
- 我们对较短的数组进行了二分查找,所以时间复杂度是 O(log(min(m,n))
- 空间复杂度:O(1)
- 只使用了几个变量来存值,所以空间复杂度为O(1)
相关文章:

Leetcode算法系列| 4. 寻找两个正序数组的中位数
目录 1.题目2.题解C# 解法一:合并List根据长度找中位数C# 解法二:归并排序后根据长度找中位数C# 解法三:方法二的优化,不真实添加到listC# 解法四:第k小数C# 解法五:从中位数的概念定义入手 1.题目 给定两个…...

Java整合APNS推送消息-IOS-APP(基于.p12推送证书)
推送整体流程 1.在开发者中心申请对应的证书(我用的是.p12文件) 2.苹果手机用户注册到APNS,APNS将注册的token返回给APP(服务端接收使用)。 3.后台服务连接APNS,获取连接对象 4.后台服务构建消息载体 5.后台…...

C语言strcpy函数用法
C语言strcpy函数用法 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天,让我们一起深入了解C语言中的strcpy函数,这是一个在字符串处理中非…...
汽车服务品牌网站建设的作用是什么
汽车服务涵盖多个层面,在保修维护这一块更是精准到了车内车外,无论是品牌商还是市场中各维修部,都能给到车辆很好的维修养护服务。如今车辆的人均拥有量已经非常高,也因此市场中围绕汽车相关的从业者也比较多。 首先就是拓客引流…...
【iOS】UICollectionView
文章目录 前言一、实现简单九宫格布局二、UICollectionView中的常用方法和属性1.UICollectionViewFlowLayout相关属性2.UICollectionView相关属性 三、协议和代理方法:四、九宫格式的布局进行升级五、实现瀑布流布局实现思路实现原理代码调用顺序实现步骤实现效果 总…...
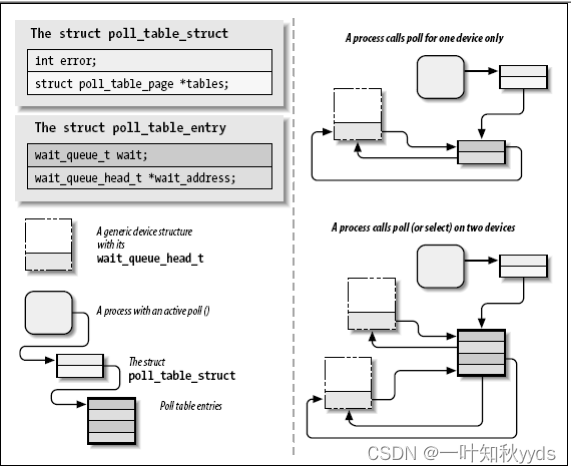
Linux poll 和 select 机制
poll select 介绍 使用非阻塞 I/O 的应用程序常常使用 poll, select, 和 epoll 系统调用. poll, select 和 epoll 本质上有相同的功能: 每个允许一个进程来决定它是否可读或者写一个 或多个文件而不阻塞. 这些调用也可阻塞进程直到任何一个给定集合的文件描述符可用来 读或写.…...
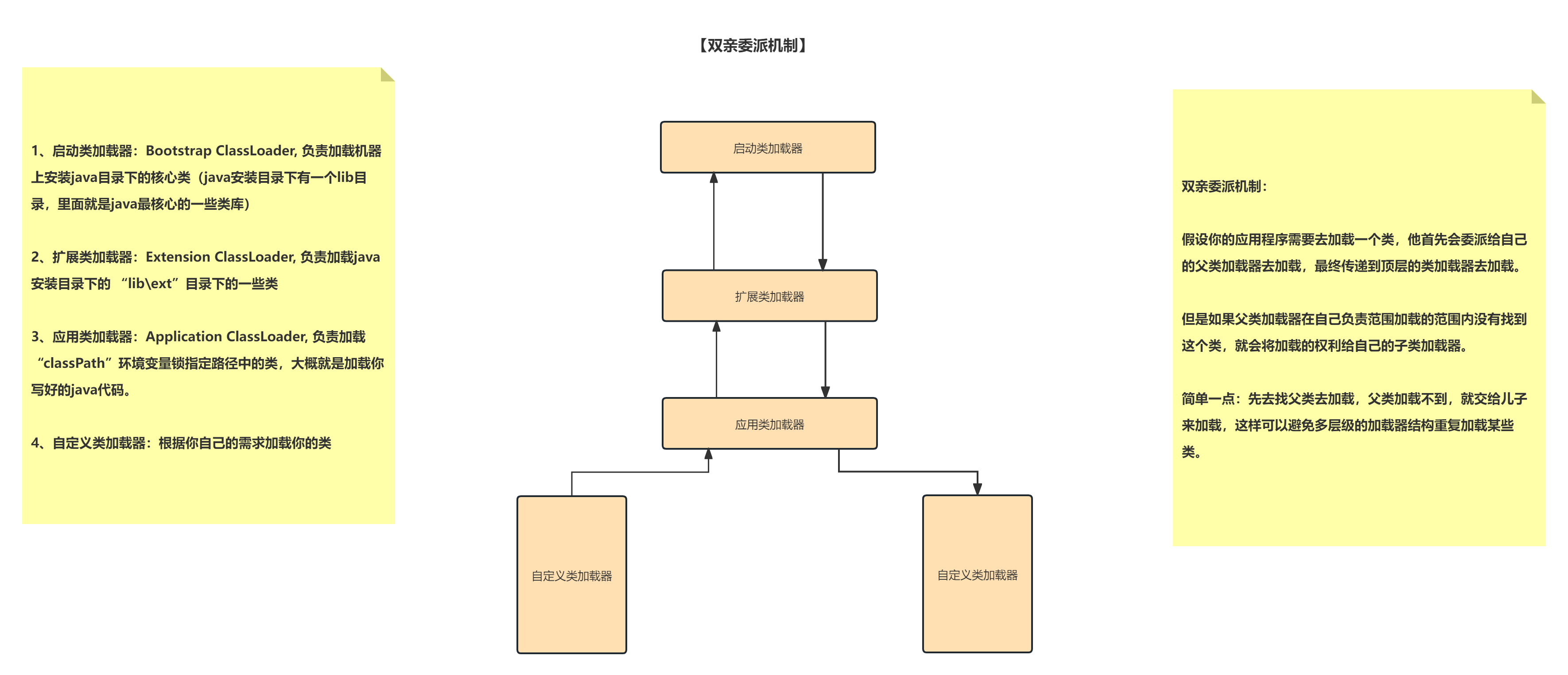
【JVM基础】 JVM 如何加载一个类以及类加载机制
文章目录 1、什么时候一个类会被加载?1、包含 main 方法的主类2、非 包含 main 方法的主类,什么时候去加载? 3、类加载器如何加载一个类?1、验证阶段:2、准备阶段:3、解析阶段:4、初始化&#x…...

Android Studio使用Genymotion
1. Genymotion介绍 GenyMotion速度之快令人发指,模拟效果堪比真机调试,支持绝大部分的模拟器功能,甚至包括语音,Google Now,支持eclipse, android studio。非常适合用来开发和演示效果。 2. Genymotion下载 Genymotio…...

Mysql sql_mode参数配置
今天在使用数据库查询时使用了Group语句,遇到问题: SELECT t1.UnderlyingInstrumentID, t2.* FROM t_OptionInstrument t1 LEFT JOIN t_Instrument t2 ON t2.InstrumentID t1.UnderlyingInstrumentID GROUP BY t1.UnderlyingInstrumentID > 1055 - …...

SpringIOC之AbstractMessageSource
博主介绍:✌全网粉丝5W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验…...

详解Vue3中的基础路由和动态路由
本文主要介绍Vue3中的基础路由和动态路由。 目录 一、基础路由二、动态路由 Vue3中的路由使用的是Vue Router库,它是一个官方提供的用于实现应用程序导航的工具。Vue Router在Vue.js的核心库上提供了路由的功能,使得我们可以在单页应用中实现页面的切换、…...
)
Mysql四种事务隔离级别(简易理解)
读未提交:简单理解就是读到没有提交事务的执行结果;读已提交:简单理解就是只能读到已经提交的事务执行结果;可重复读:简单理解就是确保并发读取数据库时,读到的数据一致,这是mysql默认隔离级别&…...
react中使用redux最简单最方便的方式,配合rematch简化操作,5分钟学会
react中使用状态管理的方式也很多,比如redux和mobx等,今天这一片就讲一下redux的入门到熟练使用,主要是要理解它redux的组成有哪些,到怎么创建,和组建中怎么使用三个问题。这里先放上官网文档,不理解的地方…...
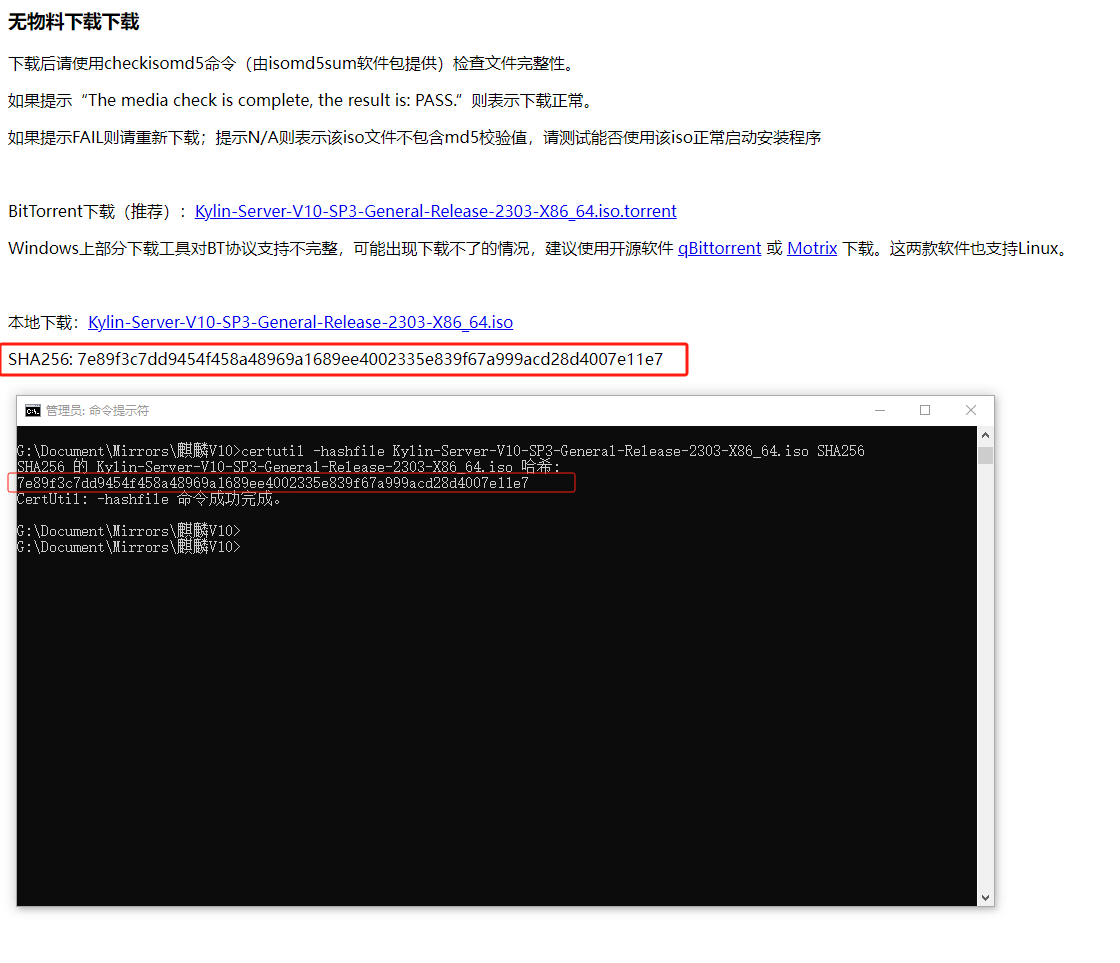
vmware安装中标麒麟高级服务器操作系统软件 V7.0操作系统
vmware安装中标麒麟高级服务器操作系统软件 V7.0操作系统 1、下载中标麒麟高级服务器操作系统软件 V7.0镜像2、安装中标麒麟高级服务器操作系统软件 V7.0操作系统 1、下载中标麒麟高级服务器操作系统软件 V7.0镜像 官方提供使用通道 访问官网 链接: https://www.kylinos.cn/ 下…...

OpenCV | 霍夫变换:以车道线检测为例
霍夫变换 霍夫变换只能灰度图,彩色图会报错 lines cv2.HoughLinesP(edge_img,1,np.pi/180,15,minLineLength40,maxLineGap20) 参数1:要检测的图片矩阵参数2:距离r的精度,值越大,考虑越多的线参数3:距离…...

【C#与Redis】--目录
1. 介绍 2. Redis 数据结构 3. Redis 命令 3.1 基本命令 3.2 字符串命令 3.3 哈希命令 3.4 列表命令 3.5 集合命令 3.6 有序集合命令 4. C# 操作 Redis 4.1 使用 Redis 库 4.2 连接 Redis 服务器 4.3 操作 Redis 数据结构 4.5 执行 Redis 命令 5. 高级主题 5.1 Redis 事…...

html旋转相册
一、实验题目 做一个旋转的3d相册,当鼠标停留在相册时,相册向四面散开 二、实验代码 <!DOCTYPE html> <html lang"zh"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" con…...

Plantuml之对象图语法介绍(十九)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...
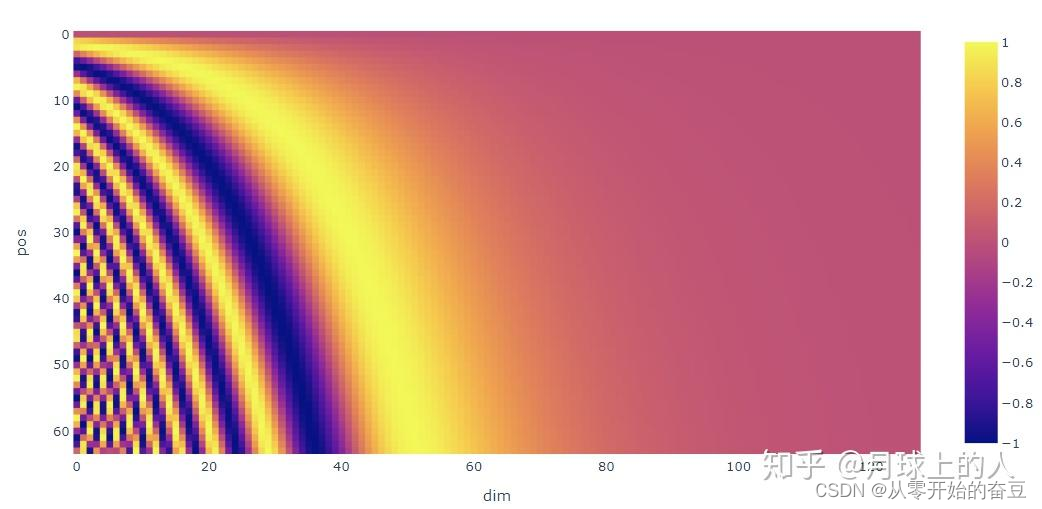
深度学习(八):bert理解之transformer
1.主要结构 transformer 是一种深度学习模型,主要用于处理序列数据,如自然语言处理任务。它在 2017 年由 Vaswani 等人在论文 “Attention is All You Need” 中提出。 Transformer 的主要特点是它完全放弃了传统的循环神经网络(RNN&#x…...
, Filter(), Find(), Map(), Negate(), Position())
R语言中的函数28:Reduce(), Filter(), Find(), Map(), Negate(), Position()
文章目录 介绍Reduce()实例 Filter()实例 Find()实例 Map()实例 Negate()实例 Position()实例 介绍 R语言中的Reduce(), Filter(), Find(), Map(), Negate(), Position()是base包中的一些高级函数。随后,很多包也给这些函数提供了更多的扩展。 Reduce() 该函数根…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...
