模式识别与机器学习(十):梯度提升树
1.原理
提升方法实际采用加法模型(即基函数的线性组合)与前向分步算法。以决策树为基函数的提升方法称为提升树(boosting tree)。对分类问题决策树是二叉分类树,对回归问题决策树是二叉回归树。提升树模型可以表示为决策树的加法模型:
f M ( x ) = ∑ m = 1 M T ( x ; θ m ) f_M(x)=\sum_{m=1}^MT(x;\theta_m) fM(x)=m=1∑MT(x;θm)
其中, T ( x ; θ m ) T(x;\theta_{m}) T(x;θm)表示决策树, θ m \theta_{m} θm为决策树参数,M为树的个数。
而梯度提升树的具体步骤如下:
1.初始化 f 0 ( x ) = 0 f_{0}(x)=0 f0(x)=0,并选取损失函数 L ( y , f ( x ) ) \mathrm{~L(y,f(x))} L(y,f(x));
2.对于 m = 0 , 1 , ⋯ , M \mathrm{m}=0,1,\cdots,\mathrm{M} m=0,1,⋯,M
(1).计算负梯度:
− g m ( x i ) = − ∂ ( L ( y , f ( x i ) ) ) ∂ f ( x i ) f ( x ) = f m − 1 ( x ) -\mathrm{g_m(x_i)=-\frac{\partial\left(L\bigl(y,f(x_i)\bigr)\right)}{\partial f(x_i)}_{f(x)=f_{m-1}(x)}} −gm(xi)=−∂f(xi)∂(L(y,f(xi)))f(x)=fm−1(x)
(2).以负梯度 − g m ( x i ) -\mathrm{g_{m}(x_{i})} −gm(xi)为预测值,训练一个回归树 T ( x ; θ m ) T(x;\theta_{m}) T(x;θm);
(3).更新 f m ( x ) = f m − 1 ( x ) + ρ T ( x ; θ m ) f_{m}(x)=f_{m-1}(x)+\rho T(x;\theta_{m}) fm(x)=fm−1(x)+ρT(x;θm);
3.经过M次迭代后取得的模型即为
f M ( x ) = ∑ m = 1 M ρ T ( x ; θ m ) f_M(x)=\sum_{m=1}^M\rho T(x;\theta_m) fM(x)=m=1∑MρT(x;θm)
这里的 ρ \rho ρ为学习率,可用来防止过拟合。
此次实验用梯度提升树来实现多分类任务,在这种情况下输出模型经过softmax函数转化为每个类别的置信概率,从而实现分类目标。
2.代码
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建梯度提升树分类器
clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0, max_depth=1, random_state=42)# 训练模型
clf.fit(X_train, y_train)# 预测测试集
y_pred = clf.predict(X_test)# 打印预测结果
print(y_pred)
我们使用了鸢尾花数据集,这是一个常用的多类别分类数据集。我们首先加载数据,然后划分为训练集和测试集。然后,我们创建一个梯度提升树分类器,并使用训练集对其进行训练。最后,我们使用训练好的模型对测试集进行预测,并打印出预测结果。
GradientBoostingClassifier的参数n_estimators表示弱学习器的最大数量,learning_rate表示学习率,max_depth表示每个弱学习器(决策树)的最大深度,这些参数都可以根据需要进行调整。
相关文章:
:梯度提升树)
模式识别与机器学习(十):梯度提升树
1.原理 提升方法实际采用加法模型(即基函数的线性组合)与前向分步算法。以决策树为基函数的提升方法称为提升树(boosting tree)。对分类问题决策树是二叉分类树,对回归问题决策树是二叉回归树。提升树模型可以表示为决…...
)
《剑指offer》Java版--12.矩阵中的路径(DFS+剪枝)
剑指offer原题:矩阵中的路径 请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再…...

AI智能体的介绍
最近几个月 随着大语言模型的持续火爆 利用大模型来构建AI智能体的研究呢 也陆续进入了人们的视野 AI智能体这个概念呢 也逐渐的流行开来 先是斯坦福大学谷歌的研究者们 成功的构建了一个虚拟小镇 小镇上的居民呢不再是人 而是25个AI的智能体 他们的行为呢 比人类角…...
)
Java设计模式-单例模式(Singleton)
Java中实现单例模式有几种不同的方式,每种方式都有其特点和适用场景。下面是两种常用的实现方式:懒汉式和饿汉式。 懒汉式(线程安全) 懒汉式单例是指在第一次被引用时才会创建实例。为了确保线程安全,可以使用同步方法或同步块。 public class SingletonLazy {private sta…...
若依vue如何展示一个HTML页面(或者展示Markdown文档)
一. 前言 ⚠ 本文是展示Markdown的方法,不能直接前端编辑Markdown文档. 二. 准备部分 用Typora编辑器打开需要导出html页面,我这里使用Typora来导出 1. 先将md文件导出成html 2. 将导出好的文件放在若依vue的pubilc下(文件可以是中文) 三. 代码部分 1.使用v-html来展示HT…...
)
优化for循环(js的问题)
性能优化 var array [];for (let index 0; index < array.length; index) {// do something }// 优化后 for (let index 0, len array.length; index < len; index) {// do something } 算法优化 // 求和:1 2 3 4 ... 100 var sum 0; for (let i …...
如何更好的去理解源码
前言 这篇文章我准备来聊一聊如何去阅读开源项目的源码。 在聊如何去阅读源码之前,先来简单说一下为什么要去阅读源码,大致可分为以下几点原因: 最直接的原因,就是面试需要,面试喜欢问源码,读完源码才可以…...

c# opencv 获取多边形中心点
在C#中使用OpenCV获取多边形的中心点,可以按照以下步骤进行: 首先,你需要找到图像中的轮廓。这可以通过FindContours方法实现: using OpenCvSharp;Mat src new Mat("your_image_path", ImreadModes.Grayscale); Mat …...
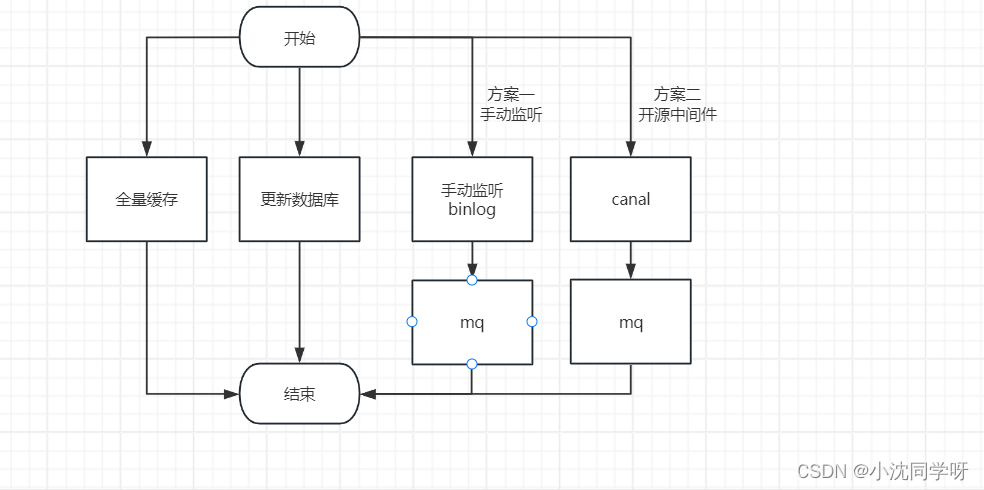
Redis数据一致解决方案
文章目录 前言技术积累查询缓存业务流程更新缓存业务流程 更新缓存问题解决方案写在最后 前言 当前的应用服务很多都有着高并发的业务场景,对于高并发的解决方案一般会用到缓存来降低数据库压力,并且还能够提高系统性能减少请求耗时,比如我们…...

安捷伦DSOX2024A示波器
参考波形 示波器的非易失参考波形存储器可以存储两个波形。比较这些参考波形与实时波形,并对已存储数据进行后分析和测量。您也可将波形数据存储到移动USB 存储器设备。这些数据还能调用到示波器的两个参考存储器的其中一个,进行全面的波形测量和分析。为…...

Leetcode算法系列| 4. 寻找两个正序数组的中位数
目录 1.题目2.题解C# 解法一:合并List根据长度找中位数C# 解法二:归并排序后根据长度找中位数C# 解法三:方法二的优化,不真实添加到listC# 解法四:第k小数C# 解法五:从中位数的概念定义入手 1.题目 给定两个…...

Java整合APNS推送消息-IOS-APP(基于.p12推送证书)
推送整体流程 1.在开发者中心申请对应的证书(我用的是.p12文件) 2.苹果手机用户注册到APNS,APNS将注册的token返回给APP(服务端接收使用)。 3.后台服务连接APNS,获取连接对象 4.后台服务构建消息载体 5.后台…...

C语言strcpy函数用法
C语言strcpy函数用法 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天,让我们一起深入了解C语言中的strcpy函数,这是一个在字符串处理中非…...
汽车服务品牌网站建设的作用是什么
汽车服务涵盖多个层面,在保修维护这一块更是精准到了车内车外,无论是品牌商还是市场中各维修部,都能给到车辆很好的维修养护服务。如今车辆的人均拥有量已经非常高,也因此市场中围绕汽车相关的从业者也比较多。 首先就是拓客引流…...
【iOS】UICollectionView
文章目录 前言一、实现简单九宫格布局二、UICollectionView中的常用方法和属性1.UICollectionViewFlowLayout相关属性2.UICollectionView相关属性 三、协议和代理方法:四、九宫格式的布局进行升级五、实现瀑布流布局实现思路实现原理代码调用顺序实现步骤实现效果 总…...
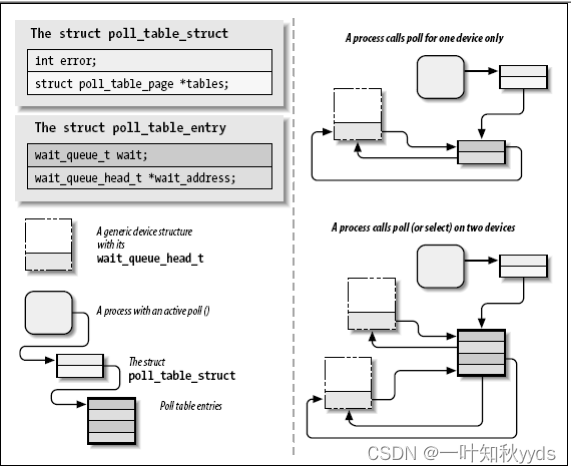
Linux poll 和 select 机制
poll select 介绍 使用非阻塞 I/O 的应用程序常常使用 poll, select, 和 epoll 系统调用. poll, select 和 epoll 本质上有相同的功能: 每个允许一个进程来决定它是否可读或者写一个 或多个文件而不阻塞. 这些调用也可阻塞进程直到任何一个给定集合的文件描述符可用来 读或写.…...
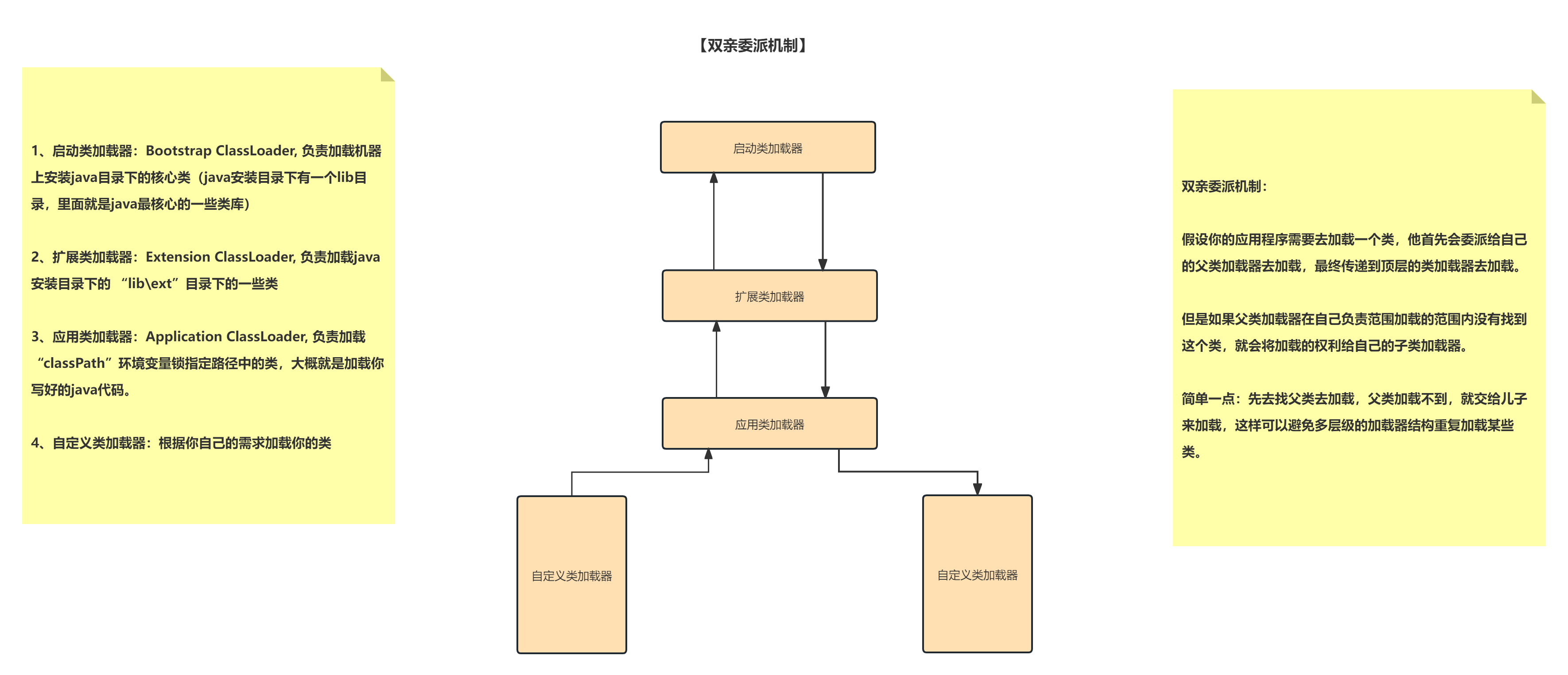
【JVM基础】 JVM 如何加载一个类以及类加载机制
文章目录 1、什么时候一个类会被加载?1、包含 main 方法的主类2、非 包含 main 方法的主类,什么时候去加载? 3、类加载器如何加载一个类?1、验证阶段:2、准备阶段:3、解析阶段:4、初始化&#x…...

Android Studio使用Genymotion
1. Genymotion介绍 GenyMotion速度之快令人发指,模拟效果堪比真机调试,支持绝大部分的模拟器功能,甚至包括语音,Google Now,支持eclipse, android studio。非常适合用来开发和演示效果。 2. Genymotion下载 Genymotio…...

Mysql sql_mode参数配置
今天在使用数据库查询时使用了Group语句,遇到问题: SELECT t1.UnderlyingInstrumentID, t2.* FROM t_OptionInstrument t1 LEFT JOIN t_Instrument t2 ON t2.InstrumentID t1.UnderlyingInstrumentID GROUP BY t1.UnderlyingInstrumentID > 1055 - …...

SpringIOC之AbstractMessageSource
博主介绍:✌全网粉丝5W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
