「数据结构」二叉树2
🎇个人主页:Ice_Sugar_7
🎇所属专栏:初阶数据结构
🎇欢迎点赞收藏加关注哦!
文章目录
- 🍉前言
- 🍉链式结构
- 🍉遍历二叉树
- 🍌前序遍历
- 🍌中序遍历
- 🍌后序遍历
- 🍉计数
- 🍌求结点数
- 🍌求叶子结点数
- 🍌求第k层结点数
- 🍉树的深度
- 🍉查找结点
- 🍉构建二叉树
- 🍉销毁二叉树
- 🍉层序遍历
- 🍉判断是否为完全二叉树
- 🍌补充
- 🍉写在最后
🍉前言
在上一篇文章中我们讲了二叉树的顺序结构,但是普通二叉树因为结点不连续,没法使用顺序结构,这就需要使用链式结构进行存储。本文将讲解二叉树的链式结构及常见函数的实现
🍉链式结构
一个结点分为三个部分:存放当前结点的数值的数据域、分别指向左、右子树的指针
typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;
🍉遍历二叉树
二叉树有三种遍历方式,通过递归实现
需要根据使用场景选择不同的遍历方式
🍌前序遍历
先访问根结点,接着是左子树,最后访问右子树(这里的“访问”指的是把结点的数值打印出来)
采用递归,那就要将大问题拆分为小问题,直到问题无法再继续拆分
●现在要访问左子树,那可以把问题拆解为“依次访问它的根结点、左子树、右子树”,拆解若干次之后,会抵达叶子结点,再往下就是空结点了,此时没法继续拆解问题,也就是到达递归的终点了,需要回归了
●右子树也同理
void BinaryTreePrevOrder(BTNode* root) {if (!root) { cout << "NULL" << " "; //为了方便观察,所以把NULL也打印出来return;}cout << root->_data << " ";BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}
有了前序遍历作为参照,那中后序遍历也就很轻松就能写出来了,只要调整一下打印语句的位置就ok了,下面直接上代码
🍌中序遍历
void BinaryTreePrevOrder(BTNode* root) {if (!root) { cout << "NULL" << " "; //为了方便观察,所以把NULL也打印出来return;}BinaryTreePrevOrder(root->_left);cout << root->_data << " ";BinaryTreePrevOrder(root->_right);
}
🍌后序遍历
void BinaryTreePrevOrder(BTNode* root) {if (!root) { cout << "NULL" << " "; //为了方便观察,所以把NULL也打印出来return;}BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);cout << root->_data << " ";
}
🍉计数
🍌求结点数
求结点数,可以转化为左子树结点数+右子树结点数+1(根结点本身),如果遇到空结点,那就返回0
int BinaryTreeSize(BTNode* root) {if (!root)return 0;return BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}
🍌求叶子结点数
和求结点数差不多,不过多了一个判断是否为叶子结点的语句,如果是,就返回1
//左右结点都为空返回1
int BinaryTreeLeafSize(BTNode* root) {if (!root)return 0;if (root->_left == NULL && root->_right == NULL)return 1;//不为空or只有一个子树为空return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}
🍌求第k层结点数
这个的递归不太好找。
方法如下:
假设k为5,那么第k层相对于第一层就是第五层,而它相对第二层则是第四层,相对第三层是第三层……相对第五层就是第一层。也就是说要求第k层,实际上是求“第一层”的结点个数(有点像求一个数的阶乘时用到的递归思想)
int BinaryTreeLevelKSize(BTNode* root, int k) {assert(k > 0); //确保k为正数if (!root)return 0;if (k == 1) //此时已经递归到了第k层return 1;return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}
🍉树的深度
深度是指从根结点到叶子结点的最长距离。这个问题可以拆解为求第二层的根结点到叶子结点的最长距离+1,再拆为第三层到叶子结点的最长距离+2……最后遇到空结点就可以停下来了
最后返回左子树和右子树二者深度的较大值
代码如下:
int BinaryTreeDepth(BTNode* root) {if (!root)return 0;int LeftSize = BinaryTreeDepth(root->_left);int RightSize = BinaryTreeDepth(root->_right);return LeftSize > RightSize ? LeftSize + 1 : RightSize + 1;
}
🍉查找结点
要在二叉树里面查找值为x的结点。每次递归先找左子树,找到就返回,找不到就去找右子树。
下面两个条件满足其一,递归终止:①到空结点时返回NULL;②找到值为x的结点就返回该结点
代码如下:
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {if (!root)return NULL;if (root->_data == x)return root;BTNode* ret = BinaryTreeFind(root->_left, x);if (ret) //如果左子树找到指定结点,就不用找右子树了return ret;return BinaryTreeFind(root->_right, x);
}
🍉构建二叉树
现在已知一个数组,它是某二叉树前序遍历的结果,该数组会用#表示空结点,现在要我们通过这个数组来构建原二叉树
●通过递归来构建。每次递归时数组当前位置的元素如果不为#,就创建一个结点,然后将它和双亲结点连起来。
●既然要让结点间能够连接起来,那函数就要返回结点或者NULL。这样在递归的过程中可以将新创建的结点或者NULL和双亲结点连接起来
●递归的停止条件就是遇到#,此时返回NULL,
BTNode* BinaryTreeCreate(BTDataType* a, int n, int pi) { //n:数组大小 pi:指向数组下标if (a[pi] == '#') {++pi;return NULL;}BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->_data = a[pi++]; //数组赋值给node之后记得++node->_left = BinaryTreeCreate(a, n, pi); //连接左子树node->_right = BinaryTreeCreate(a, n, pi); //连接右子树return node; //返回根结点
}
这里要说一下这个pi,因为我们使用递归而非迭代,需要知道数组下标(即递归到哪个元素了),所以要传下标
🍉销毁二叉树
要采用后序遍历销毁结点,如果采用前序或中序,根结点都不是最后销毁的,这样会导致无法找到某一边的子树。比如采用中序,销毁左子树后把根结点给销毁了,那就没法找到右子树了
void BinaryTreeDestory(BTNode** root) {assert(root);if (*root == NULL)return;BinaryTreeDestory(&(*root)->_left);BinaryTreeDestory(&(*root)->_right);free(*root);*root = NULL;
}
🍉层序遍历
前面讲的前、中、后序遍历都属于深度优先遍历,以前序遍历为例,会先递推到最左下的结点,然后才回归,这是一个纵向的过程。
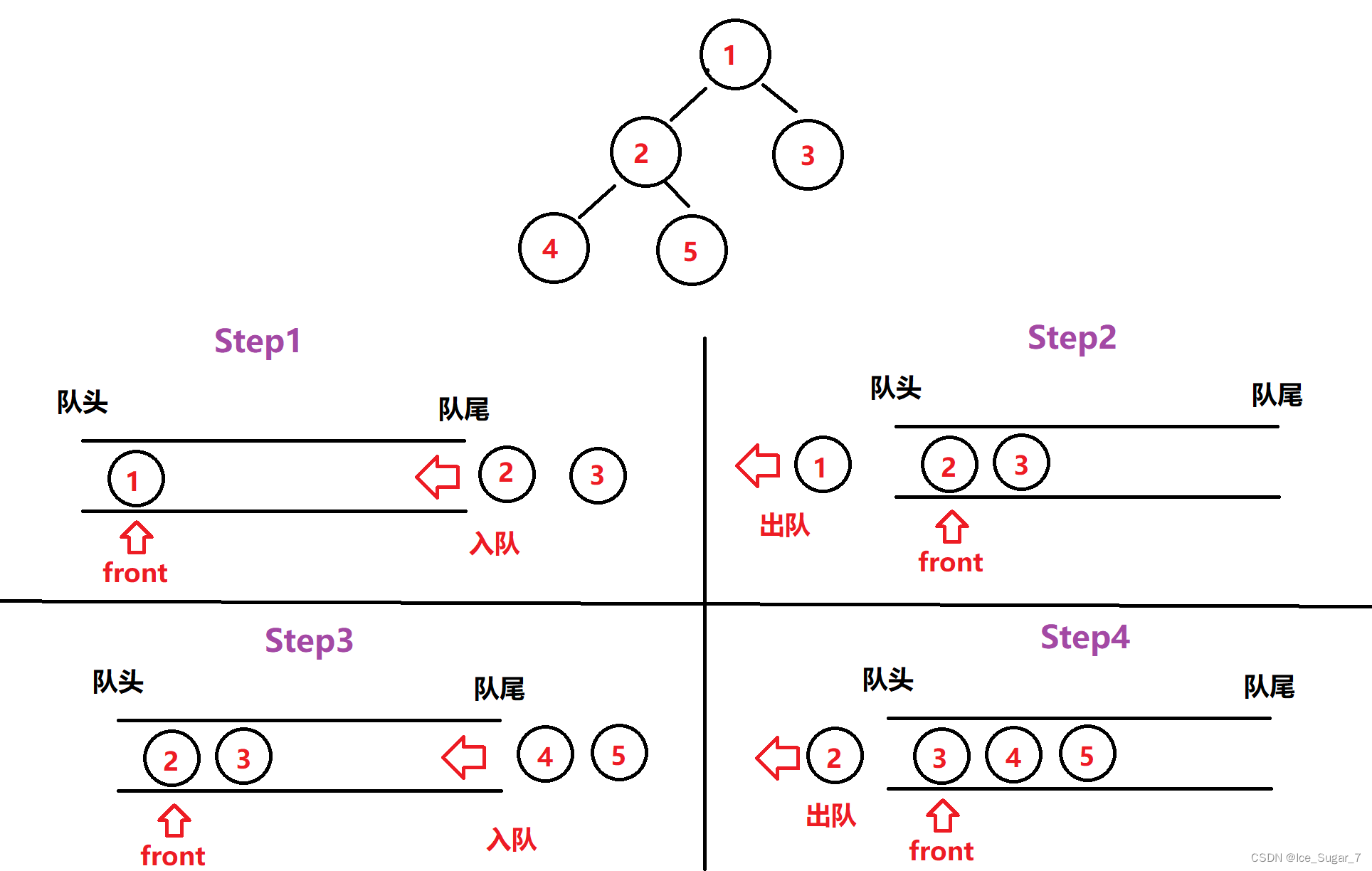
而层序遍历又称为广度优先遍历,顾名思义,就是一层一层遍历。这种遍历需要使用队列
具体的过程为:先让根结点入队,标记为队首front,然后将它的左右子树根结点入队(前提是结点不为空,如果为空那就不用入),再让队头的根结点出队,子树的根结点成为新的队头。
重复上面这个过程,直到队列为空
举个栗子:
代码如下:
void BinaryTreeLevelOrder(BTNode* root) {if (!root)return;Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)) {QDataType front = QueueFront(&q); //队首元素cout << QueueFront(&q)->_data << endl;QueuePop(&q); //队首元素出队 然后要让它的左右子树入队if (root->_left)QueuePush(&q, front->_left);if (root->_left)QueuePush(&q, front->_right);}QueueDestroy(&q);
}🍉判断是否为完全二叉树
完全二叉树的特点就是结点连续,根据这个性质,我们采用层序遍历,不过这次层序遍历需要把空结点也入队。如果遇到空结点时后面的结点也全为空,那就是完全二叉树;反之,如果后面还有非空结点,那就不是
简而言之,我们要判断front为空结点时队列剩下的元素是否全为空
代码如下:
bool BinaryTreeComplete(BTNode* root) {if (!root)return true;Queue q;QueueInit(&q);QueuePush(&q, root);BTNode* front = root;while (!QueueEmpty(&q)){front = QueueFront(&q); if (front == NULL) //队首是空结点,就是遇到的第一个空结点,跳出循环break;//空结点也要入队QueuePush(&q, front->_left);QueuePush(&q, front->_right);QueuePop(&q); //队首元素出队}//到这里的时候说明已经遇到空结点//接下来要排查剩下的结点,看看是否有非空结点while (!QueueEmpty(&q)) {front = QueueFront(&q);QueuePop(&q);if (front) { //若遇到不为空的结点,说明不是完全二叉树QueueDestroy(&q);return false;}}//到这里说明全部都是空结点,那就是完全二叉树了QueueDestroy(&q);return true;
}
🍌补充
while (!QueueEmpty(&q)) {front = QueueFront(&q);QueuePop(&q);if (front) { QueueDestroy(&q);return false;}}
我们已经将队首的结点pop掉,那后面的if语句还能否访问front?
答案是可以。因为front保存队首结点的值,而这个值是二叉树结点的地址,即指向二叉树的结点。(刚才上面那个图是为了方便理解,所以才把front的箭头指向队首)pop掉队首结点并不会影响树的结点,所以还是可以访问的
🍉写在最后
以上就是本篇文章的全部内容,如果你觉得本文对你有所帮助的话,那不妨点个小小的赞哦!(比心)
相关文章:

「数据结构」二叉树2
🎇个人主页:Ice_Sugar_7 🎇所属专栏:初阶数据结构 🎇欢迎点赞收藏加关注哦! 文章目录 🍉前言🍉链式结构🍉遍历二叉树🍌前序遍历🍌中序遍历&#x…...

数据处理系列课程 01:谈谈数据处理在数据分析中的重要性
一、数据分析 可能很多朋友第一次听到这个名词,那么我们先来谈一谈什么是数据分析。 数据分析是指用适当的统计分析方法对收集来的大量数据进行分析,将它们加以汇总和理解,以求最大化地开发数据的功能,发挥数据的作用。数据分析是…...

C++卡码网题目55--右旋字符串
卡码网题目链接 字符串的右旋转操作是把字符串尾部的若干个字符转移到字符串的前面。给定一个字符串 s 和一个正整数 k,请编写一个函数,将字符串中的后面 k 个字符移到字符串的前面,实现字符串的右旋转操作。 例如,对于输入字符…...
)
八股文打卡day8——计算机网络(8)
面试题:什么是强缓存和协商缓存? 我的回答: 强缓存:浏览器不需要发送请求到服务器,直接从浏览器缓存中获取数据。浏览器不需要和服务器进行交互就可以获取数据,这样极大提高了页面访问速度。 协商缓存&am…...

亚马逊推出 Graviton4:具有 536.7 GBps 内存带宽的 96 核 ARM CPU
如今,许多云服务提供商都设计自己的芯片,但亚马逊网络服务 (AWS) 开始领先于竞争对手,目前其子公司 Annapurna Labs 开发的处理器可以与 AMD 和英特尔的处理器竞争。本周,AWS 推出了 Graviton4 SoC,这是一款基于 ARM 的…...

跨域问题的解决
1.什么是跨域? 浏览器从一个域名的网页去请求另外一个域名的资源时,域名、端口或者协议不同都是跨域 2.跨域的解决方案 设置CORS响应头∶后端可以在HTTP响应头中添加相关的CORS标头,允许特定的源(域名、协议、端口)访问资源。S…...
)
Typro+PicGo自动上传图片(图床配置)
文章目录 所需工具主要配置 TyproPicGo自动上传图片(图床配置) 使用Typro编写 的markdown(md)文件如果存在图片,并且想快速发布博文的话,常使用PiGO工具配置图床服务器来管理图片。 所需工具 TyporaPicGo(依赖Nodejs和插件super…...
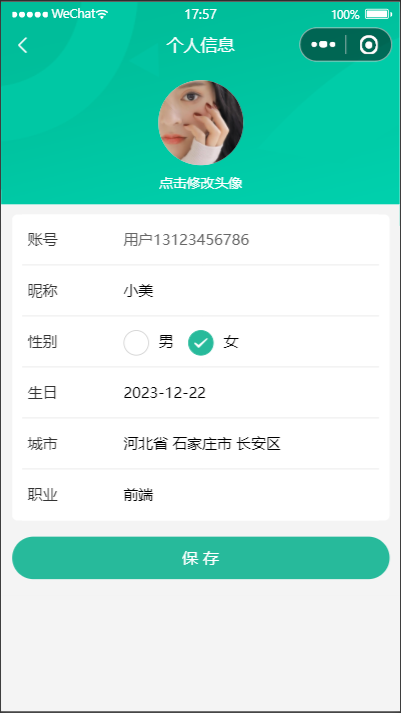
uniapp实战 -- 个人信息维护(含选择图片 uni.chooseMedia,上传文件 uni.uploadFile,获取和更新表单数据)
效果预览 相关代码 页面–我的 src\pages\my\my.vue <!-- 个人资料 --><view class"profile" :style"{ paddingTop: safeAreaInsets!.top px }"><!-- 情况1:已登录 --><view class"overview" v-if"membe…...

企业如何建立价值评估体系?
企业绩效评价体系是指由一系列与绩效评价相关的评价制度、评价指标体系、评价方法、评价标准以及评价机构等形成的有机整体。企业的评价系统大致可以分为以下四个层次: 第一、岗位评价系统,主要针对不同岗位之间的评估。例如,企业中一般业务…...

华为安防监控摄像头
华为政企42 华为政企 目录 上一篇华为政企城市一张网研究报告下一篇华为全屋wifi6蜂鸟套装标准...

[node] Node.js 缓冲区Buffer
[node] Node.js 缓冲区Buffer 什么是BufferBuffer 与字符编码Buffer 的方法概览Buffer 的实例Buffer 的创建写入缓冲区从 Buffer 区读取数据将 Buffer 转换为 JSON 对象Buffer 的合并Buffer 的比较Buffer 的覆盖Buffer 的截取--sliceBuffer 的长度writeUIntLEwriteUIntBE 什么是…...
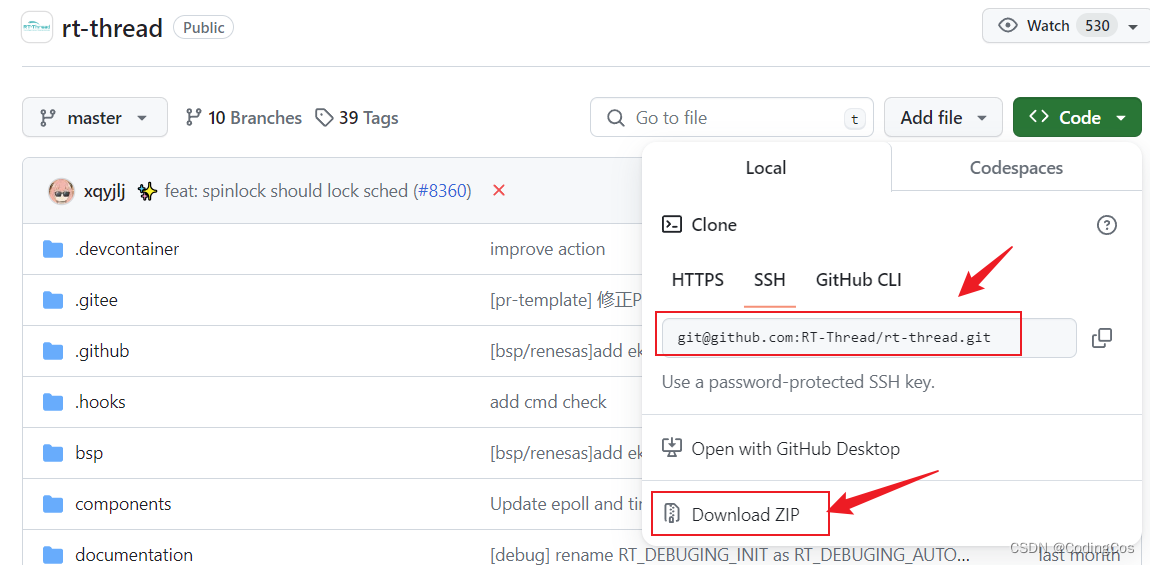
【ARM Cortex-M 系列 5 -- RT-Thread renesas/ra4m2-eco 移植编译篇】
文章目录 RT-Thread 移植编译篇编译os.environ 使用示例os.putenv使用示例python from 后指定路径 编译问题_POSIX_C_SOURCE 介绍编译结果 RT-Thread 移植编译篇 本文以瑞萨的ra4m2-eco 为例介绍如何下载rt-thread 及编译的设置。 RT-Thread 代码下载: git clone …...

功能强大的开源数据中台系统 DataCap 1.18.0 发布
推荐一套基于 SpringBoot 开发的简单、易用的开源权限管理平台,建议下载使用: https://github.com/devlive-community/authx 推荐一套为 Java 开发人员提供方便易用的 SDK 来与目前提供服务的的 Open AI 进行交互组件:https://github.com/devlive-commun…...
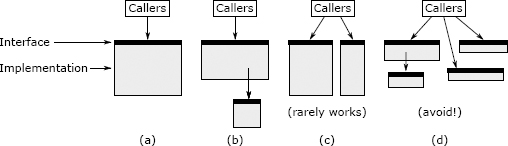
A Philosophy of Software Design 学习笔记
前言 高耦合,低内聚,降低复杂度:在软件迭代中,不关注软件系统结构,导致软件复杂度累加,软件缺乏系统设计,模块混乱,一旦需求增加、修改或者优化,改变的代价无法评估&…...
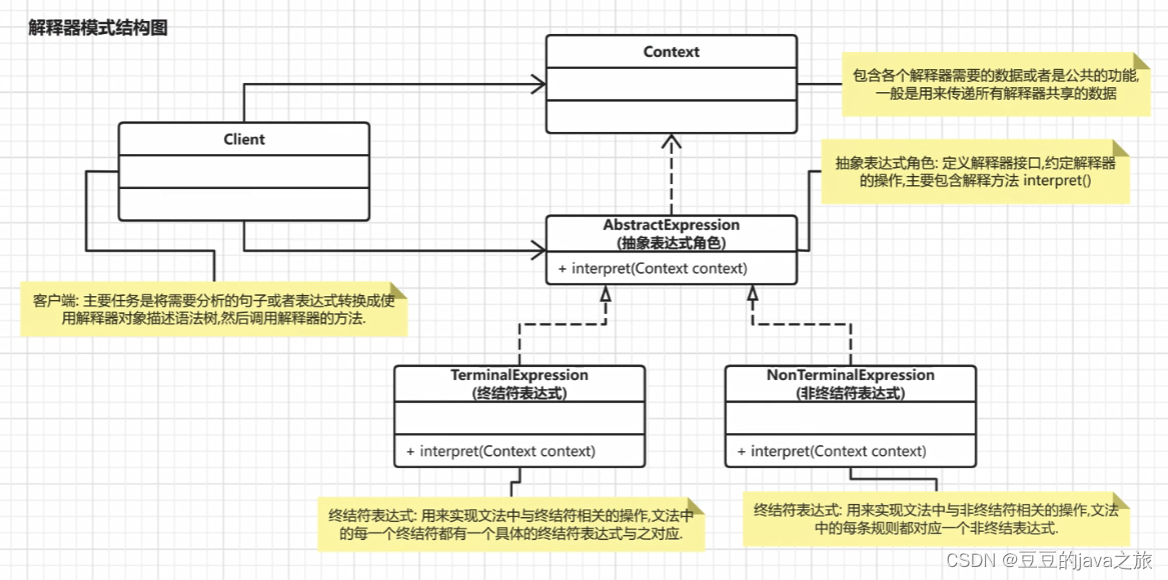
设计模式----解释器模式
一、简介 解释器模式使用频率并不高,通常用来构建一个简单语言的语法解释器,它只在一些非常特定的领域被用到,比如编译器、规则引擎、正则表达式、sql解析等。 解释器模式是行为型设计模式之一,它的原始定义为:用于定义…...
:Conda、RPM、文件权限、apt-get(更新中...)
Linux常用命令(一):Conda、RPM、文件权限、apt-get(更新中...
文章目录 一、Conda二、RPM三、文件权限四、apt-get 一、Conda Conda是一个开源的软件包管理系统和环境管理系统,用于安装和管理软件包及其依赖项。它主要用于Python编程语言,但也可以用于其他语言的项目。Conda可以帮助用户创建不同版本的Python环境&a…...

3 个适用于 Mac 电脑操作的 Android 数据恢复最佳工具 [附步骤]
在当今的数字时代,无论是由于意外删除、系统故障还是其他原因,从 Android 设备中丢失数据不仅会带来不便,而且会造成非常严重的后果。特别是对于Mac用户来说,从Android手机恢复数据是一个很大的麻烦。幸运的是,随着许多…...
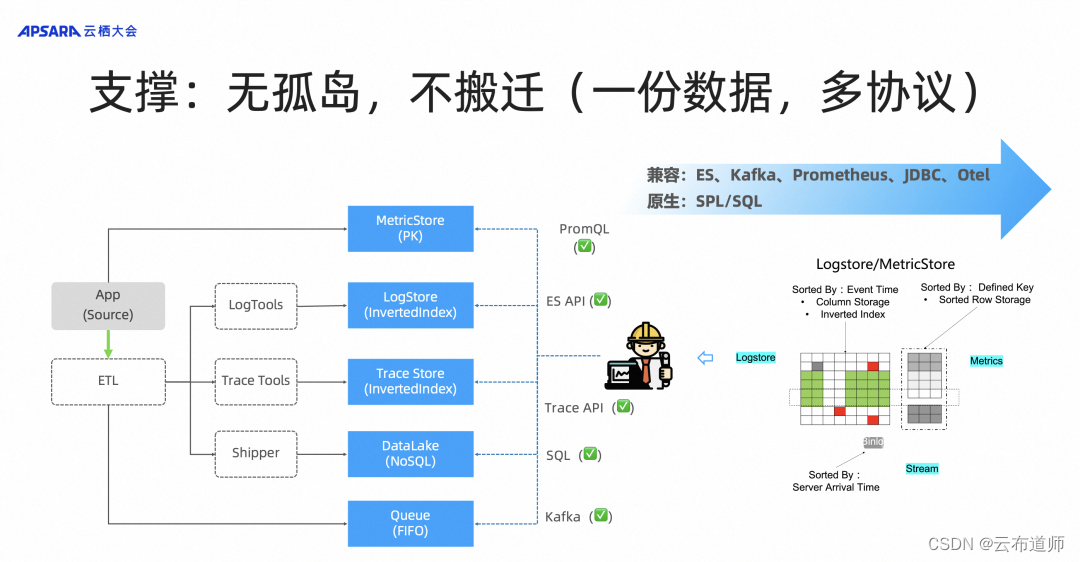
日志服务 SLS 深度解析:拥抱云原生和 AI,基于 SLS 的可观测分析创新
云布道师 10 月 31 日,杭州云栖大会上,日志服务 SLS 研发负责人简志和产品经理孟威等人发表了《日志服务 SLS 深度解析:拥抱云原生和 AI,基于 SLS 的可观测分析创新》的主题演讲,对阿里云日志服务 SLS 产品服务创新以…...

MinIO客户端之rm
MinIO提供了一个命令行程序mc用于协助用户完成日常的维护、管理类工作。 官方资料 mc rm 删除指定的对象。 准备待删除的对象,查看对象,命令如下: ./mc ls local1/bkt2/控制台的输出,如下: [2023-12-16 01:52:54 …...

【Linux笔记】文件和目录操作
🍎个人博客:个人主页 🏆个人专栏:Linux学习 ⛳️ 功不唐捐,玉汝于成 目录 前言 命令 ls (List): pwd (Print Working Directory): cp (Copy): mv (Move): rm (Remove): 结语 我的其他博客 前言 学习Linux命令…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
