前缀和+单调双队列+贪心:LeetCode2945:找到最大非递减数组的长度
本文涉及知识点
C++算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频
单调双队列 贪心
题目
给你一个下标从 0 开始的整数数组 nums 。
你可以执行任意次操作。每次操作中,你需要选择一个 子数组 ,并将这个子数组用它所包含元素的 和 替换。比方说,给定数组是 [1,3,5,6] ,你可以选择子数组 [3,5] ,用子数组的和 8 替换掉子数组,然后数组会变为 [1,8,6] 。
请你返回执行任意次操作以后,可以得到的 最长非递减 数组的长度。
子数组 指的是一个数组中一段连续 非空 的元素序列。
示例 1:
输入:nums = [5,2,2]
输出:1
解释:这个长度为 3 的数组不是非递减的。
我们有 2 种方案使数组长度为 2 。
第一种,选择子数组 [2,2] ,对数组执行操作后得到 [5,4] 。
第二种,选择子数组 [5,2] ,对数组执行操作后得到 [7,2] 。
这两种方案中,数组最后都不是 非递减 的,所以不是可行的答案。
如果我们选择子数组 [5,2,2] ,并将它替换为 [9] ,数组变成非递减的。
所以答案为 1 。
示例 2:
输入:nums = [1,2,3,4]
输出:4
解释:数组已经是非递减的。所以答案为 4 。
示例 3:
输入:nums = [4,3,2,6]
输出:3
解释:将 [3,2] 替换为 [5] ,得到数组 [4,5,6] ,它是非递减的。
最大可能的答案为 3 。
参数范围:
1 <= nums.length <= 105
1 <= nums[i] <= 105
枚举最后一个子数组nums(j,i]
假定结果向量为vRet
nums[0,j] 需要记录两个子状态:最有一个子数组的和,vRet的长度(操作前的子数组数量)。枚举这些状态时间复杂度O(n),枚举i时间复杂度O(n),枚举j时间复杂度O(n)。故总时间复杂度o(n3)。合并nums[0,j]和nums(j,i]有两种操作:
操作一:nums(j,i]全部合并到vRet[j]的最后一个元素。无前提条件。
操作二:nums(j,i]成为新元素。前天条件nums(j,i]大于vRet[j]的最后一个元素。
贪心:不存在len > len2且v1 > v2
令nums[0,i)合法分成n段,最后一段的值为fin,即分成一段,最后的值为fi1,分成两段,最后的值为fi2。
令nums[0,j)…fjn。
证明:对于任意数组(子数组),fxn 一定 大与等于fxn+1。x是j,j等…
n==1: fx1 为整个数组的和,fx2为数组第二部分的和。显然成立。
n >1 用反证法:
假定可以合法分成n段,分别为{a1,a2…an}
假定可以合法分成n+1段:分别为(b1,b2…bn,bn+1}。bn+1可能有多个值,取最小值
假定an < bn+1,则{a1,a2,…an-1} 和大于{b1…bn}的和 => 假定前者包括nums[0,i)后者包括nums[0,j) => i >j
则{b1,b2…bn+nums[j,i)}是nums[0,i)的一个合法分成n段,{a1…an-1} 是nums[0,i)一个合法n-1段。
bn+nums[j,i)就是fin, an-1,就是fn-1 fxn-1 >= fnx =>an-1 > bn+nums[j,i)
因为an >= an-1 => {b1,b2…bn+nums[j,i),an} 是一个nums的n+1段划分。
结合假设:an <bn+1 和 bn+1是最小值矛盾
优化后时间复杂度O(n)
如果nums[0,i)存在长度len,则nums[0,i]一定存在长度为len的结果:将nums[i]追加到最后。
判断nums[0,i]能否则在nums[0,j] 增加一个元素(nums(j,i]的和),需要判断
vPreSum[i+1] - vPreSum[j+1] >= Last[j]
即vPreSump[i+1] >= Last[j]+vPreSum[j+1]
Last[j] 是最后元素的值
Last[j]+vPreSum[j+1] 可以合并一个变量llPre。已知状态只需要保留最大长度,长度相同保留llPre最小。
此解法错误,还在摸索中。
class Solution {
public:int findMaximumLength(vector<int>& nums) {m_c = nums.size();auto vPreSum = CreatePreSum(nums);int len = 0;long long llPre = 0;int preIndex = -1;for (int i = 0; i < m_c; i++){if (vPreSum[i + 1] >= llPre){len++;llPre = vPreSum[i+1] + (vPreSum[i + 1] - vPreSum[preIndex + 1]);preIndex = i;}else{const long long curAdd = vPreSum[i+1] - vPreSum[preIndex+1] + (vPreSum[i + 1] - vPreSum[preIndex + 1]);if (curAdd < 0){llPre += curAdd;preIndex = i;}}}return len;}int m_c;
};
正确解法
下标从小到大遍历nums[i],queIndexs记录[0,i),淘汰以下:
一,j1 < j2,也就(j1,i]的和大于(j2,i]。也就是j1的最后一个数大于j2的最后一个数。llPre1 大于llPre2,也就llPre1更难匹配,淘汰j1。淘汰后:下标升序 llPre 降序。
二,j找到第一个i后,淘汰。假定j的长度为len,i1 < i2。i1可以选择{… (j,i1],(i1,i2]} 和{…{j,i2]},而i2只能选择后者,所以i1不劣与i2。
注意:如果无法长度+1,则vLast[i] = vLast[i - 1] + nums[i]
队首元素的长度和队尾元素的长度相差不会超过1
双向队列中的下标升序,也就是长度升序。
假定新入队的长度是len,则被淘汰的队首长度为len-1。由于是升序,所以队中元素的长度都大于等于len-1,小于等于len
template<class T = long long >
vector<T> CreatePreSum(const vector<int>& nums)
{vector<T> preSum;preSum.push_back(0);for (int i = 0; i < nums.size(); i++){preSum.push_back (preSum[i]+ nums[i]);}return preSum;
}class Solution {
public:int findMaximumLength(vector<int>& nums) {m_c = nums.size();auto vPreSum = CreatePreSum(nums);vector<int> vRet(m_c,1),vLast(m_c,nums.front());std::deque<int> queIndexs;queIndexs.emplace_back(0);auto Pre = [&](const int index) {return vPreSum[index + 1] + vLast[index]; };for (int i = 1; i < m_c; i++){vRet[i] = vRet[i - 1];vLast[i] = vLast[i - 1] + nums[i];while (queIndexs.size() && (vPreSum[i + 1] >= Pre(queIndexs.front()))){vRet[i] = vRet[queIndexs.front()]+1;vLast[i] = vPreSum[i + 1] - vPreSum[queIndexs.front() + 1];queIndexs.pop_front();}while (queIndexs.size() && (Pre(queIndexs.back()) >= Pre(i))){queIndexs.pop_back();}queIndexs.emplace_back(i);}return vRet.back();}int m_c;
};
错误解法
class Solution {
public:
int findMaximumLength(vector& nums) {
stack sta;
int i = 0;
while (i < nums.size())
{
long long cur = 0;
while (sta.size() && (i < nums.size()) && (sta.top() > cur + nums[i]))
{
cur += nums[i++];
}
if (i >= nums.size())
{
break;//理论上需要栈顶的值,由于我需要的是数量,所以可以不修改
}
sta.emplace(cur+ nums[i++]);
}
return sta.size();
}
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用C++ 实现。

相关文章:

前缀和+单调双队列+贪心:LeetCode2945:找到最大非递减数组的长度
本文涉及知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 单调双队列 贪心 题目 给你一个下标从 0 开始的整数数组 nums 。 你可以执行任意次操作。每次操作中,你需要选择一个 子数组 ,并将这个子数组用它所…...
【微服务】springboot整合kafka-stream使用详解
目录 一、前言 二、kafka stream概述 2.1 什么是kafka stream 2.2 为什么需要kafka stream 2.2.1 对接成本低 2.2.2 节省资源 2.2.3 使用简单 2.3 kafka stream特点 2.4 kafka stream中的一些概念 2.5 Kafka Stream应用场景 三、环境准备 3.1 搭建zk 3.1.1 自定义d…...
什么是动态代理?
目录 一、为什么需要代理? 二、代理长什么样? 三、Java通过什么来保证代理的样子? 四、动态代理实现案例 五、动态代理在SpringBoot中的应用 导入依赖 数据库表设计 OperateLogEntity实体类 OperateLog枚举 RecordLog注解 上下文相…...
【OAuth2】:赋予用户控制权的安全通行证--原理篇
🥳🥳Welcome Huihuis Code World ! !🥳🥳 接下来看看由辉辉所写的关于OAuth2的相关操作吧 目录 🥳🥳Welcome Huihuis Code World ! !🥳🥳 一.什么是OAuth? 二.为什么要用OAuth?…...
【K8s】2# 使用kuboard管理K8s集群(kuboard安装)
文章目录 安装 Kuboard v3部署计划 安装登录测试 安装 Kuboard v3 部署计划 在正式安装 kuboard v3 之前,需做好一个简单的部署计划的设计,在本例中,各组件之间的连接方式,如下图所示: 假设用户通过 http://外网IP:80…...

爬虫是什么?起什么作用?
【爬虫】 如果把互联网比作一张大的蜘蛛网,数据便是放于蜘蛛网的各个节点,而爬虫就是一只小蜘蛛,沿着网络抓取自己得猎物(数据)。这种解释可能更容易理解,官网的,就是下面这个。 爬虫是一种自动…...

代码随想录27期|Python|Day24|回溯法|理论基础|77.组合
图片来自代码随想录 回溯法题目目录 理论基础 定义 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。 回溯是递归的副产品,只要有递归就会有回溯。回溯函数也就是递归函数,指的都是一个函数。 基本问题 组合问题(无序&…...
 : 大数据按分区导出数据)
mysql(49) : 大数据按分区导出数据
代码 import com.alibaba.gts.flm.base.util.Mysql8Instance;import java.io.BufferedWriter; import java.io.File; import java.io.FileWriter; import java.math.BigDecimal; import java.util.ArrayList; import java.util.Iterator; import java.util.List; import java.u…...
阿里云ECS配置IPv6后,如果无法访问该服务器上的网站,可检查如下配置
1、域名解析到这个IPv6地址,同一个子域名可以同时解析到IPv4和IPv6两个地址,这样就可以给网站配置ip4和ipv6双栈; 2、在安全组规则开通端口可访问,设定端口后注意授权对象要特殊设置“源:::/0” 3、到服务器nginx配置处,增加端口…...
基于SSM的双减后初小教育课外学习生活活动平台的设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

HTTP前端请求
目录 HTTP 请求1.请求组成2.请求方式与数据格式get 请求示例post 请求示例json 请求示例multipart 请求示例数据格式小结 3.表单3.1.作用与语法3.2.常见的表单项 4.session 原理5.jwt 原理 HTTP 请求 1.请求组成 请求由三部分组成 请求行请求头请求体 可以用 telnet 程序测…...

前端性能优化二十四:花裤衩模板第三方库打包
(1). 工作原理: ①. externals配置在所创建bundle时:a. 会依赖于用户环境(consumers environment)中的依赖,防止将某些import的包(package)打包到bundle中b. 在运行时(runtime)再去从外部获取这些扩展依赖(external dependencies)②. webpack会检测这些组件是否在externals中注…...
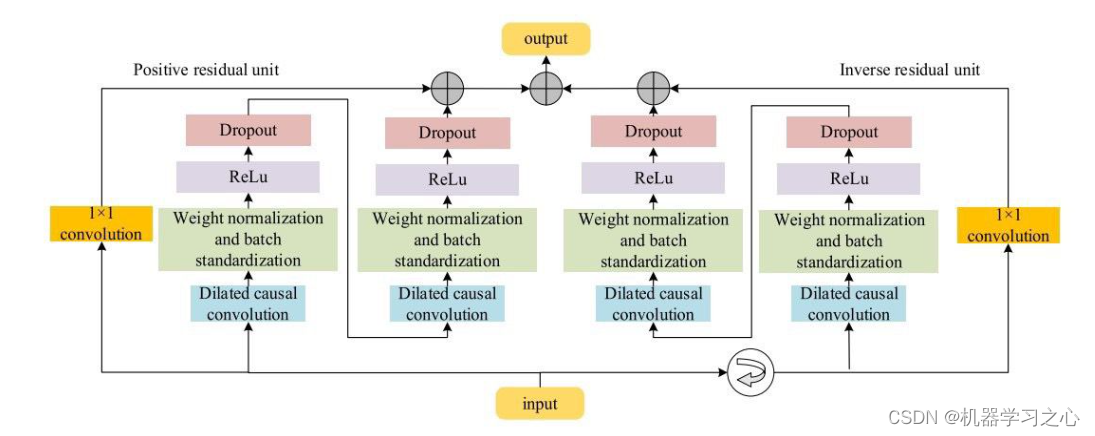
多维时序 | MATLAB实现BiTCN-Multihead-Attention多头注意力机制多变量时间序列预测
多维时序 | MATLAB实现BiTCN-Multihead-Attention多头注意力机制多变量时间序列预测 目录 多维时序 | MATLAB实现BiTCN-Multihead-Attention多头注意力机制多变量时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 多维时序 | MATLAB实现BiTCN-Multihea…...

Qt的简单游戏实现提供完整代码
文章目录 1 项目简介2 项目基本配置2.1 创建项目2.2 添加资源 3 主场景3.1 设置游戏主场景配置3.2 设置背景图片3.3 创建开始按钮3.4 开始按钮跳跃特效实现3.5 创建选择关卡场景3.6 点击开始按钮进入选择关卡场景 4 选择关卡场景4.1场景基本设置4.2 背景设置4.3 创建返回按钮4.…...

SpringMVC之文件的下载
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 SpringMVC之文件的下载 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、文件下载实现…...
计算机组成原理第6章-(算术运算)【下】
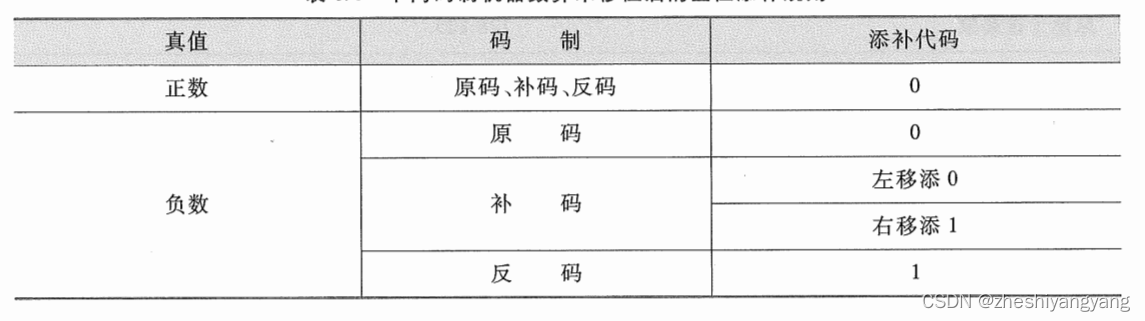
移位运算 对于有符号数的移位称为算术移位,对于无符号数的移位称为逻辑移位。 算术移位规则【极其重要】 对于正数的算术移位,且不管是何种机器数【原码、反码、补码】,移位后出现的空位全部填0。 而对于负数的算术移位,机器数不同,移位后的规则也不同。 对于负数的原…...

【开题报告】基于微信小程序的校园资讯平台的设计与实现
1.选题背景与意义 随着移动互联网的快速发展,微信成为了人们日常生活中不可或缺的工具之一。在校园生活中,学生们对于校园资讯的获取和交流需求也越来越高。然而,传统的校园资讯发布方式存在信息不及时、传播范围有限等问题,无法…...

VUE前端导出文件之file-saver插件
VUE前端导出文件之file-saver插件 安装 npm install file-saver --save # 如使用TS开发,可安装file-saver的TypeScript类型定义 npm install types/file-saver --save-dev如果需要保存大于 blob 大小限制的非常大的文件,或者没有 足够的 RAM࿰…...

【Earth Engine】协同Sentinel-1/2使用随机森林回归实现高分辨率相对财富(贫困)制图
目录 1 简介与摘要2 思路3 效果预览4 代码思路5 完整代码6 后记 1 简介与摘要 最近在做一些课题,需要使用Sentinel-1/2进行机器学习制图。 然后想着总结一下相关数据和方法,就花半小时写了个代码。 然后再花半小时写下这篇博客记录一下。 因为基于多次拍…...
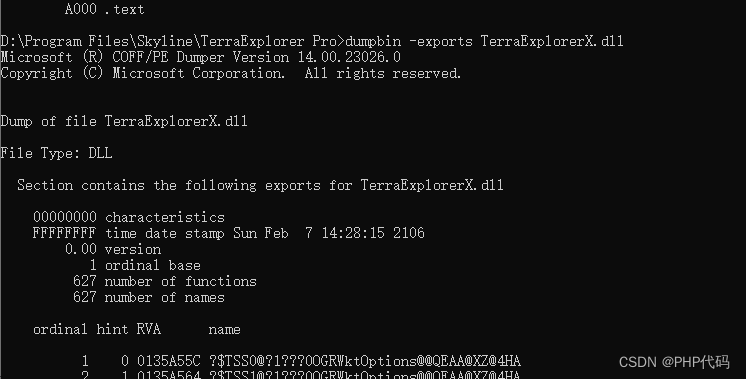
C++ 检测 是不是 com组件 的办法 已解决
在日常开发中,遇到动态库和 com组件库的调用 无法区分。检测是否com组件的办法 在头部文件,引入文件 如果能编译成功说明是 com组件,至于动态库如何引入,还在观察中 最简单办法 regsvr32 TerraExplorerX.dll 是com 组件 regs…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
