2023-3-2 刷题情况
迷宫
题目描述
这天, 小明在玩迷宫游戏。
迷宫为一个 n×n 的网格图, 小明可以在格子中移动, 左上角为 (1,1), 右 下角 (n,n) 为终点。迷宫中除了可以向上下左右四个方向移动一格以外, 还有 m 个双向传送门可以使用, 传送门可以连接两个任意格子。
假如小明处在格子 (x1,y1)(x_1,y _1)(x1,y1), 同时有一个传送门连接了格子 (x1,y1)(x_1,y_1)(x1,y1) 和 (x2,y2)(x_2,y_2)(x2,y2), 那么小明既可以花费 1 的步数向上下左右四个方向之一走一格 (不能 越过边界), 也可以花费 1 的步数通过传送门走到格子 (x2,y2)(x_2,y_2 )(x2,y2) 去。
而对于同一个迷宫, 小明每次进入的初始格子是在这 n×n 个格子中均匀随 机的 (当然运气好可以直接随机到终点), 他想知道从初始格子走到终点的最短 步数的期望值是多少。
输出描述
输入共 1+m 行, 第一行为两个正整数 n,m 。后面 m 行, 每行四个正整数 ,xi1,yi1,xi2,yi2x_{i1},y_{i1},x_{i2},y_{i2}xi1,yi1,xi2,yi2表示第 i 个传送门连接的两个格 子坐标。
输出描述
输出共一行, 一个浮点数表示答案 (请保留两位小数)。
样例
样例输入
2 1
1 1 2 2
样例输出
0.75
样例解释
计算的是一个期望值,是矩阵中所有节点的最短路到终点的总和/ 矩阵大小。
思路
边权为1,还是可以使用bfs,不过由于传送门的存在,需要进行特殊判断。
代码实现
import java.util.*;public class Main{public static class pair{int first;int second;public pair(int first, int second) {this.first = first;this.second = second;}}static int[][] dir = {{1, 0},{-1, 0},{0, 1},{0, -1}};public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt(), m = sc.nextInt();int[][] matrix = new int[n + 1][n + 1];boolean[][] vis = new boolean[n + 1][n + 1];List<pair> list[][] = new ArrayList[n + 1][n + 1];for(int i = 0; i < m; i++) {int a = sc.nextInt(), b = sc.nextInt(), c = sc.nextInt(), d = sc.nextInt();if(list[a][b] == null) list[a][b] = new ArrayList<>();if(list[c][d] == null) list[c][d] = new ArrayList<>();list[a][b].add(new pair(c, d));list[c][d].add(new pair(a, b));}matrix[n][n] = 0;vis[n][n] = true; Queue<pair> queue = new ArrayDeque<>();queue.offer(new pair(n, n));while(!queue.isEmpty()) {pair cur = queue.poll();if(list[cur.first][cur.second] != null) {for(pair c : list[cur.first][cur.second]) {if(!vis[c.first][c.second]) {vis[c.first][c.second] = true;matrix[c.first][c.second] = matrix[cur.first][cur.second] + 1;queue.offer(c);}}}for(int[] d : dir) {int x = cur.first + d[0];int y = cur.second + d[1];if(0 < x && x <= n && 0 < y && y <= n && !vis[x][y]) {vis[x][y]= true; matrix[x][y] = matrix[cur.first][cur.second] + 1; queue.offer(new pair(x, y));}}}long sum = 0;for(int[] r : matrix) {for(int c : r)sum += c;}System.out.printf("%.2f", (double)((sum * 1.0) / (n * n)));sc.close();}
}
相关文章:

2023-3-2 刷题情况
迷宫 题目描述 这天, 小明在玩迷宫游戏。 迷宫为一个 nn 的网格图, 小明可以在格子中移动, 左上角为 (1,1), 右 下角 (n,n) 为终点。迷宫中除了可以向上下左右四个方向移动一格以外, 还有 m 个双向传送门可以使用, 传送门可以连接两个任意格子。 假如小明处在格子 (x1,y1)(…...
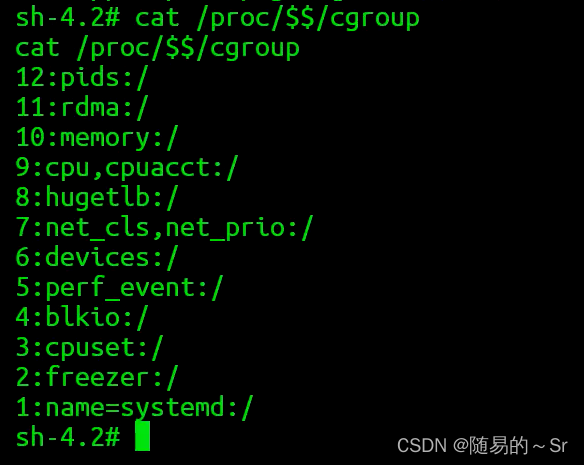
Docker SYS_ADMIN 权限容器逃逸
1.漏洞原理Docker容器不同于虚拟机,它共享宿主机操作系统内核。宿主机和容器之间通过内核命名空间(namespaces)、内核Capabilities、CGroups(control groups)等技术进行隔离。若启动docker容器时给主机一个--cap-addSY…...

【Kotlin】 yyyy-MM-dd HH:mm:ss 时间格式 时间戳 全面解读超详细
时间格式 时间格式(协议)描述gg时期或纪元。y不包含纪元的年份。不具有前导零。yy不包含纪元的年份。具有前导零。yyyy包含纪元的四位数的年份。M月份数字。一位数的月份没有前导零。MM月份数字。一位数的月份有一个前导零。MMM月份的缩写名称,在AbbreviatedMonthN…...

git repack多包使用及相关性能测试
1、git数据结构 git 中存在四种数据结构,即object包含四种,分别是tree对象、blob对象、commit对象、tag对象 1.1 blob对象 存储文件内容,内容是二进制的形式,通过SHA-1算法对文件内容和头信息进行计算得到key(文件名)。 如果一…...
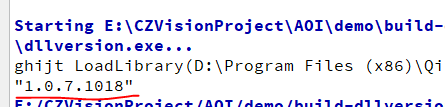
QT获取dll库文件详细信息
一、需求背景获取软件下依赖的dll库的版本信息,如下图所示版本为1.0.7.1018二、实现方法2.1步骤windows下实现,基于version.lib(version.dll)提供的函数获取这些信息首先使用GetFileVersionInfoSizeA(W)获取VersionInfo的大小,申请缓冲区&…...

常见的电脑运行卡顿原因及解决方法
大家在日常使用电脑过程中,会发现多开几个文件就卡顿,其实很多时候都跟C盘长期不清理有关,C盘的内存被下载的软件安装包、页面文件、休眠文件、更新文件等一系列的文件占据。大的文件甚至能占到20-30G,驱动人生就为大家带来几种解…...

案例08-让软件的使用者成为软件的设计者
一:背景介绍 对于需求的开发每天可能都会有上线的情况,为了防止每次上线拉取代码或者修改配置而引发的冲突以及发生了冲突应该找谁一起确定一下代码留下那一部分的情况。所以在开发的群中会有一个表格来记录每个需求上线修改的环境、是否修改数据库、是否…...

QinQ与Vlan Mapping讲解
目录 QinQ Vlan扩展 QinQ实现方式 QinQ实验配置 Vlan Mapping Vlan映射 映射方式 配置命令 QinQ Vlan扩展 QinQ全称为802.1Q-in-802.1Q,为Vlan扩展技术,在802.1Q标签报文的基础上再增加一层802.1Q标签,实现扩展Vlan空间;可…...

golang 获取token方法
package main import ( "fmt" "time" "github.com/dgrijalva/jwt-go" ) const ( SECRETKEY "202203021124355xxx" //私钥 ) // 自定义 Claims type CustomClaims struct { UserId int64 jwt.StandardClaims } func main() { //生…...
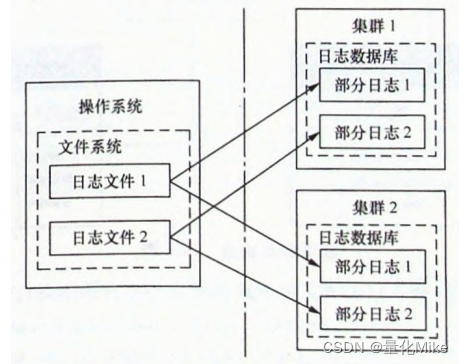
【数据库专题】数据库Mongodb之深入认知云计算三种服务方式、mongodb特点、mongodb重要进程 mongod、mongo、其他进程区别
文章目录一、什么是云计算1. IaaS:基础设施即服务2. SaaS:软件即服务3. PaaS:平台即服务二、大数据与云计算关系三、什么是MongoDB四、大数据与MongoDB五、MongoDB特点六、安装MongoDB七、重要进程介绍7.1 mongod进程7.2 mongo进程7.3 其他进程7.3.1 mongodump重建数据库7.3.2 …...
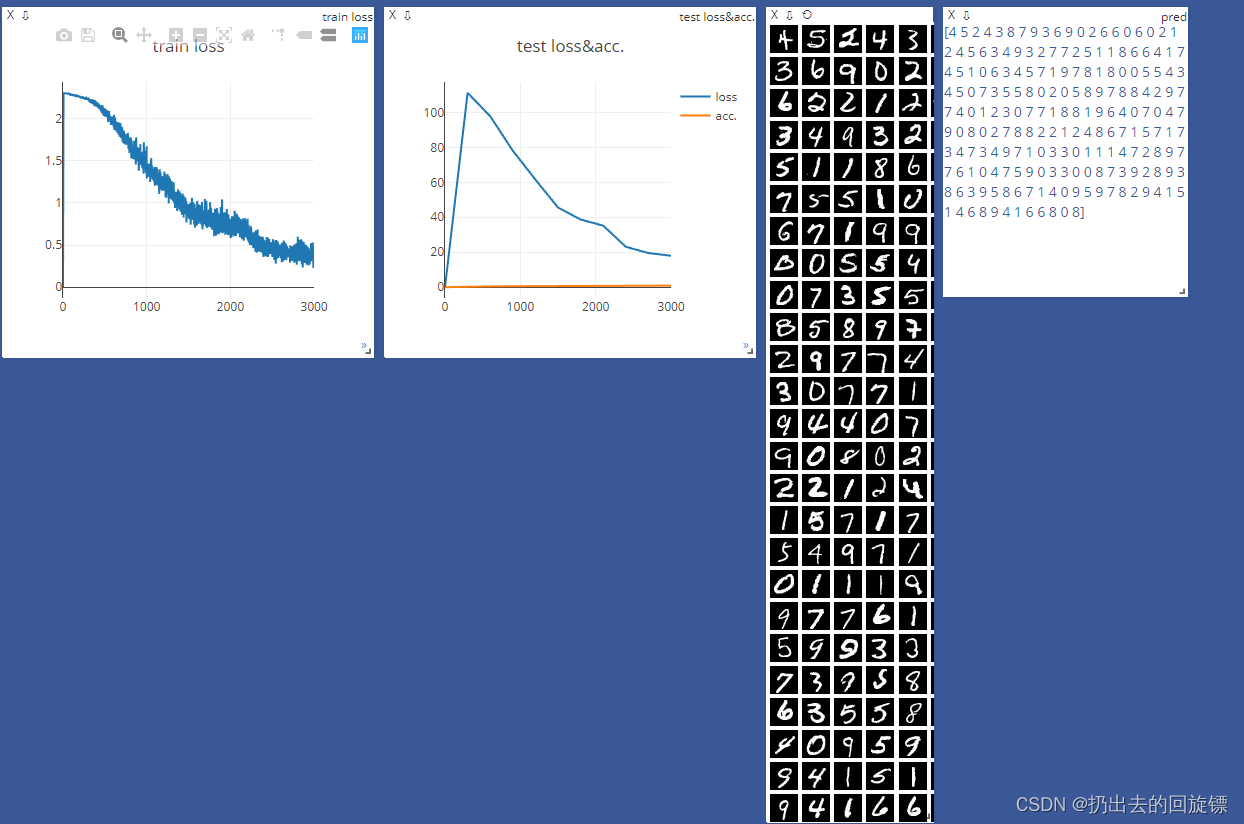
ccc-pytorch-小实验合集(4)
文章目录一、 Himmelblau 优化二、多分类实战-Mnist三、Sequential与CPU加速-Mnist四、visidom可视化一、 Himmelblau 优化 Himmelblau 是一个具有4个最优值的2维目标函数。其函数和最优值点如下: 图象绘制: import numpy as np from matplotlib impo…...

webrtc音频系列——4、RTP与RTCP协议
如果让你从0开发一套实时互动直播系统,你首先要选择网络传输协议。UDP 还是 TCP?答案是:UDP。为什么实时传输不能用 TCP ?TCP 的目的就是实现数据的可靠传输,因此他有一套 握手,发送 -> 确认,…...
)
C++枚举解读(enum)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、枚举是什么?二、使用步骤1.作用域2.隐式类型转换3.显式指定枚举值类型4.指定枚举值的值4.整形显式转换成枚举总结前言 对于开发C来说࿰…...
)
OSCP-课外5(Web图片泄露服务信息、日志中毒)
目录 一、主机发现与端口扫描 二、Web信息收集 三、系统信息收集与提权 一、主机发现与端口扫描...
汇编指令学习(ADD,SUB,MUL,DIV,XADD,INC,DEC,NEG)
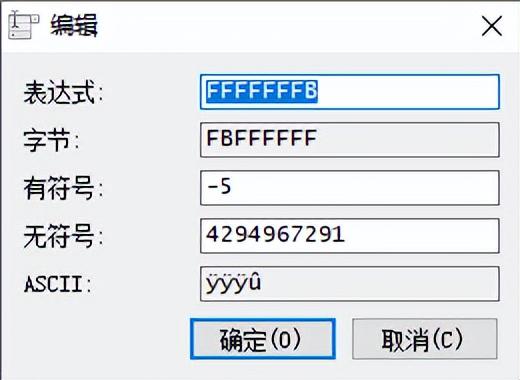
一、ADD加法操作指令将eax置1,ebx置2,运行下面命令,将结果保存到eaxadd eax,ebx扩展:adc需要再加上CF标志位的值adc eax,ebx二、SUB减法操作指令将eax置3,ebx置2,运行下面命令,将结果…...

【电源专题】案例:充电芯片损坏为什么判断是从NTC进入的EOS
最近有发现一个异常就是测试部测试测试然后充电芯片就无法使用了。通过二极管特性分析(参考文章:电源专题】案例:电源芯片厂家怎么判断电源芯片端口是否损坏)是NTC管脚已经损坏对地短路了。但是以前没有发现这个问题,最近更换了芯片后就发现的特别明显。 首先分析一下现在…...

C语言中的数据储存规则
写在开头 关于复习的相关内容其实从一开始就列出了大纲,但是迟迟没有开始复习,一方面是因为学校学业却是繁忙,另一方面还是内心对旧知识掌握不熟练需要再学一遍的畏惧和懒惰,但如今,复习必须开始了。今天我从C语言的最…...
Android kotlin实战之协程suspend详解与使用
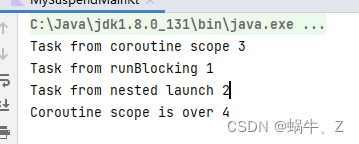
前言 Kotlin 是一门仅在标准库中提供最基本底层 API 以便各种其他库能够利用协程的语言。与许多其他具有类似功能的语言不同,async 与 await 在 Kotlin 中并不是关键字,甚至都不是标准库的一部分。此外,Kotlin 的 挂起函数 概念为异步操作提供…...

Pycharm中的Virtualenv Environment、Conda Environment
版本一 Conda Environment该不该选? 先说结论,该选,而且还是正解。前提是你打算"用Anaconda来管理各种Python环境,同时管理Python下面的各种包"。 选了Conda Environment意味着什么? 意味着你以后如果要装新的包的话…...

C++容器介绍:vector
目录vector简介使用方法1.头文件2.vector声明及初始化3.vector基本操作(1). 容量(2). 修改(3)迭代器(4)元素的访问(5)算法vector 简介 vector是表示可变大小数组的序列容器。就像数组一样,vector也采用的连续存储空间来存储元素。也就是意味着可以采用下标对vecto…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
