ZKP Mathematical Building Blocks (2)
MIT IAP 2023 Modern Zero Knowledge Cryptography课程笔记
Lecture 3: Mathematical Building Blocks (Yufei Zhao)
- Fiat Shamir heuristic
- Turn an interactive proof to a non-interactive proof
- P can simulate V
- whenever V picks a random value
- P can simulate V’s randomness by running a cryptographic hash function on the transcript so that P can’t cheat by choosing “favorable random challenges”
- Elliptic Curve
-
y 2 = x 3 + A x + B y^2 = x^3 + Ax + B y2=x3+Ax+B
-
All points in a elliptic curve make a group

-
g in the generator of the group G

-
Difficult problem:
- Discrete Log Problem on Elliptic Curve
- Secret random x generated form Zq
- Share with the public xG
- It is hard to recover x from xG
- Diffie-Hellman Key Exchange (Public key cryptography)
- Alice takes a random a mod q
- Bob takes a random b mod q
- Alice says to the public: aG
- Bob says to the public: bG
- So, Alice and Bob share a secret: abG
- Discrete Log Problem on Elliptic Curve
-
- Pairing based cryptography
- Given cyclic groups G 0 , G 1 , G T G_0, G_1, G_T G0,G1,GT all same prime order q
- a pairing is a nondegenerate bilinear map
- e : G 0 × G 1 → G T e: G_0 \times G_1 \rightarrow G_T e:G0×G1→GT
- Properties
- Bilinear
- e(x+x’, y) = e(x,y) + e(x’,y)
- e(x,y+y’) = e(x,y) + e(x,y’)
- e(ax,y) = ae(x,y) + e(x,ay)
- Nondegenerated
- With generator g 0 ∈ G 0 g_0 \in G_0 g0∈G0 and g 1 ∈ G 1 g_1 \in G_1 g1∈G1
- g T = e ( g 0 , g 1 ) ∈ G T g_T = e(g_0, g_1) \in G_T gT=e(g0,g1)∈GT
- Bilinear
- An application BLS signature scheme (Boneh-Lynn-Shacham)
- Protocol
- Keygen: s k = s sk = s sk=s, p k = s g pk = sg pk=sg
- Sign(sk,m): σ = s H ( m ) \sigma = sH(m) σ=sH(m)
- Verify(pk,m): check e ( p k , H ( m ) ) = e ( g , σ ) e(pk, H(m)) = e(g,\sigma) e(pk,H(m))=e(g,σ)
- It can be extended to allow signature aggregation
- The verifier can collect all the signatures and aggregate them into a single short signature.
- The verifier can just verify the short signature then he knows that everyone signed their messages correctly.
- Protocol
相关文章:

ZKP Mathematical Building Blocks (2)
MIT IAP 2023 Modern Zero Knowledge Cryptography课程笔记 Lecture 3: Mathematical Building Blocks (Yufei Zhao) Fiat Shamir heuristic Turn an interactive proof to a non-interactive proofP can simulate V whenever V picks a random valueP can simulate V’s ran…...
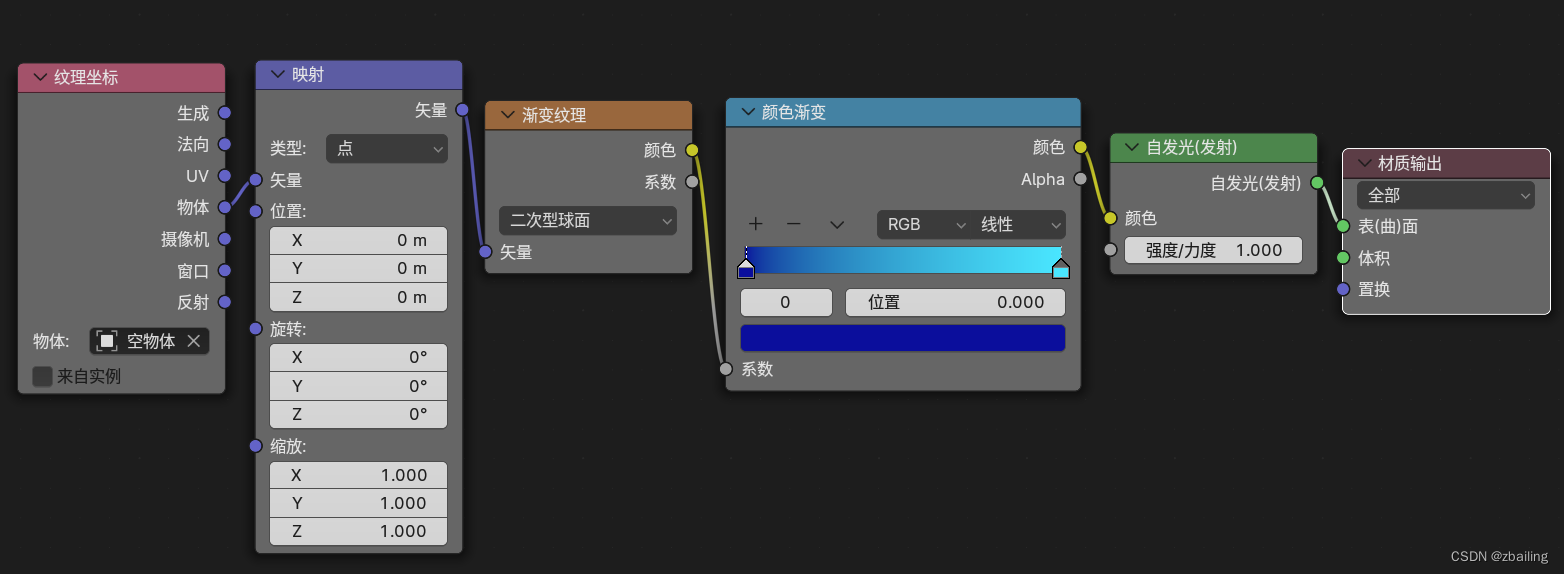
blender径向渐变材质-着色编辑器
要点: 1、用纹理坐标中的物体输出连接映射中的矢量输入 2、物体选择一个空坐标,将空坐标延z轴上移一段距离 3、空坐标的大小要缩放到和要添加材质的物体大小保持一致...

2023美团机器人研究院学术年会成功举办
2023年12月19日,深圳市美团机器人研究院学术年会在清华大学深圳国际研究生院成功落下帷幕。会议回顾了研究院成立一年来的进展和成果,并邀请了各界专家共同讨论机器人技术的未来发展趋势。此外,年会期间还举办了首届低空经济智能飞行管理挑战…...

swing快速入门(二十七)
注释很详细,直接上代码 上一篇 新增内容 1.为按钮指定图标 2. 列表框的并列 3.菜单项绑定快捷键 4.控件悬浮提示信息 5.菜单项设置小图标 6.五种布局风格右键选择切换 package swing21_30;import javax.swing.*; import java.awt.*; import java.awt.event.…...
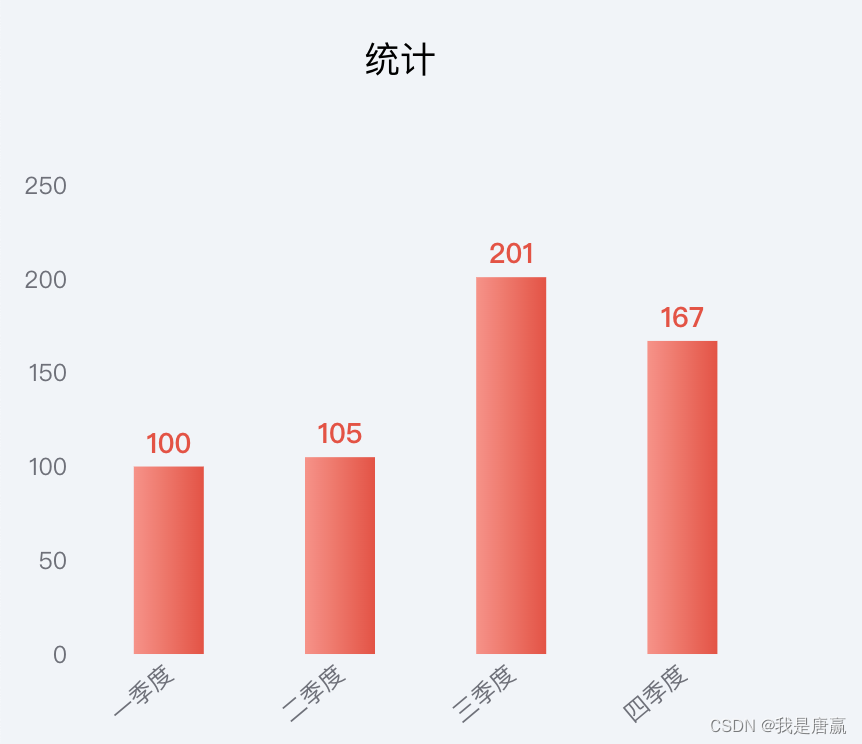
Vue 封装echarts柱状图(Bar)组件
目的:减少重复代码,便于维护 显示效果 组件代码 <template><div class"ldw-data-content-box"><div class"ldw-chilren-box"><div class"title" v-if"title">{{ title }}</div>…...
)
异常(Java)
1.异常的概念 在 Java 中,将程序执行过程中发生的不正常行为称为异常 。 1.算数异常 System.out.println(10 / 0); // 执行结果 Exception in thread "main" java.lang.ArithmeticException: / by zero 2.数组越界异常 int[] arr {1, 2, 3}; System.out.…...

vue的插槽解析
插槽 好处:组件的内容结构可定制 用slot插槽进行占位 语法: 子组件中通过slot进行占位 理解:父组件,在子组件标签嵌套的内容就会被渲染到slot地方 一、默认插槽 //子组件 <slot>slot插槽</slot> //方法一<slot name"…...
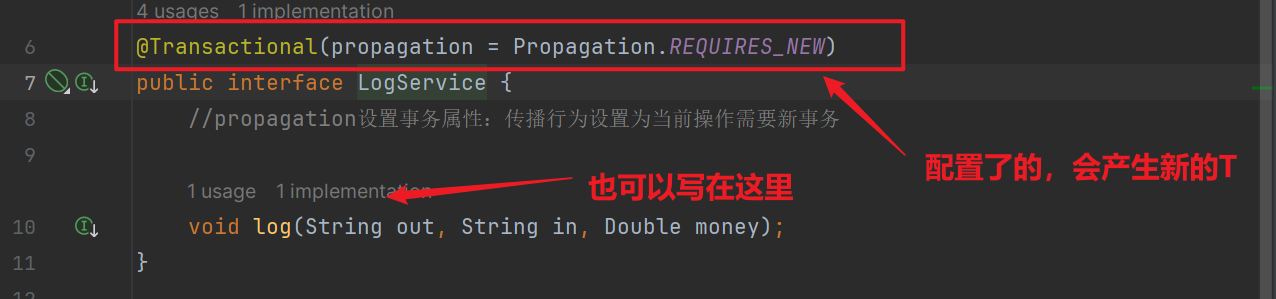
Spring(3)Spring从零到入门 - Spring整合技术及AOP事务管理
Spring(3)Spring从零到入门 - Spring整合技术及AOP事务管理 文章目录 Spring(3)Spring从零到入门 - Spring整合技术及AOP事务管理4 Spring整合技术示例4.1 Spring整合Mybatis4.1.1 Mybatis开发回顾4.1.2 整合Spring分析4.1.3 Spri…...

适配器模式学习
适配器模式(Adapter)将一个类的接口转换成客户希望的另外一个接口。Adapter 模式使得原本由于接口不兼容而不能一起工作的那些类可以一起工作。 适配器模式分为类适配器模式和对象适配器模式两种,前者类之间的耦合度比后者高,且要…...
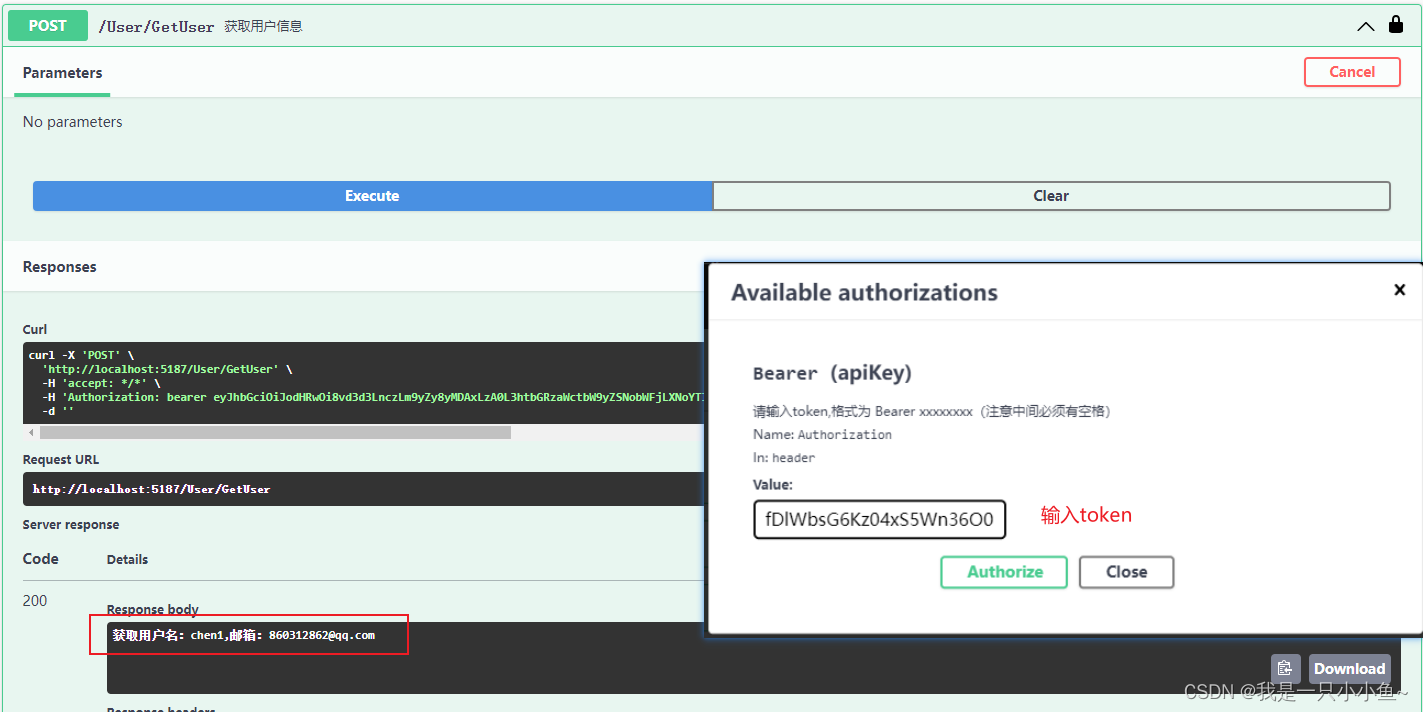
NET中使用Identity+CodeFirst+Jwt实现登录、鉴权
目录 前言 一、创建上下文类 1.自定义MyContext上下文类继承IdentityDbContext 2.在Program中添加AddDbContext服务 二、使用Migration数据迁移 1.在控制台中 依次使用add-migration 、updatebase 命令 2.如何修改表名 3.如何自定义字段 三、使用Identity实现登录、修改密码 …...

详解Keras3.0 API: Optimizers
Optimizers 优化器(Optimizer)是深度学习中用于更新模型参数的一种方法,它的目标是最小化损失函数。在训练神经网络时,我们通常使用梯度下降法来更新参数,而优化器就是实现这一过程的工具。优化器的主要作用是在每次迭…...

【数据结构】字符串匹配|BF算法|KMP算法|next数组的优化
字符串匹配算法是在实际工程中经常遇到的问题,也是各大公司笔试面试的常考题目,本文主要介绍BF算法(最好想到的算法,也最好实现)和KMP算法(最经典的) 一、BF算法 BF算法,即暴力(Bru…...

阿里云 ACK One 新特性:多集群网关,帮您快速构建同城容灾系统
云布道师 近日,阿里云分布式云容器平台 ACK One[1]发布“多集群网关”[2](ACK One Multi-cluster Gateways)新特性,这是 ACK One 面向多云、多集群场景提供的云原生网关,用于对多集群南北向流量进行统一管理。 基于 …...
vscode自定义代码片段
前言 代码片段,指的是能够帮助输入重复代码模式,比如初始页面的模板。通过 snippet ,我们仅仅输入一小段字符串,就可以在代码片引擎的帮助下,生成预定义的模板代码,接着我们还可以通过在预定义的光标位置之…...
【贪心算法】专题练习一
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析(3) 前言 1.什么是贪心算法?——贪婪鼠目寸光 贪心策…...

【JMeter】使用nmon进行性能资源监控
一、前言 在工作中可能会遇到需要在压测的时候对Linux服务器进行性能资源监控的情况。这时可以用nmon来对服务器进行监控。 二、nmon的下载安装 1.查看系统信息 shell cat /etc/os-release 结果为 shell PRETTY_NAME"Debian GNU/Linux 12 (bookworm)" NAME&…...
Unity预设体
目录 预设体是什么? 如何创建预设体? 如何修改预设体? 如何删除预设体? 预设体是什么? Unity中的预设体(Prefab)是一种可重复使用的游戏对象模板。它允许开发者创建一个或多个游戏对象&…...

Elasticsearch 写入优化探索:是什么影响了refresh 耗时?
1、问题背景: 数据写入后,refresh耗时过长,能达到1s-5s。 想通过测试,探索确认影响refresh的因素,比如:写入操作是新增还是更新,deleted文档占比是否有影响,是否有其他索引配置&…...

Java8新特性——函数式接口
目录 一、介绍 二、示例 (一)Consumer 源码解析 测试示例 (二)Comparator (三)Predicate 三、应用 四、总结 一、介绍 FunctionalInterface是一种信息注解类型,用于指明接口类型声明…...

Epson打印机连接wifi
环境 Epson L3153 打印机联通无线光猫 背景 最近家里的联通宽带不太稳定,经常断网。今天打了联通客服电话,师傅上门来,说可能是光猫用的时间太长了,换了一个新的联通光猫,问题解决。 wifi的名称是 CU_Y3ft 和 CU_Y3…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
)
MySQL基本操作(续)
第3章:MySQL基本操作(续) 3.3 表操作 表是关系型数据库中存储数据的基本结构,由行和列组成。在MySQL中,表操作包括创建表、查看表结构、修改表和删除表等。本节将详细介绍这些操作。 3.3.1 创建表 在MySQL中&#…...
和向下转型(Downcasting))
【Java基础】向上转型(Upcasting)和向下转型(Downcasting)
在面向对象编程中,转型(Casting) 是指改变对象的引用类型,主要涉及 继承关系 和 多态。 向上转型(Upcasting) ⬆️ 定义 将 子类对象 赋值给 父类引用(自动完成,无需强制转换&…...
