【贪心算法】专题练习一

欢迎来到Cefler的博客😁
🕌博客主页:那个传说中的man的主页
🏠个人专栏:题目解析
🌎推荐文章:题目大解析(3)

前言
1.什么是贪心算法?——贪婪+鼠目寸光
贪心策略:解决问题的策略,局部最优->全局最优
(1)即把解决问题的过程分为若干步
(2)解决每一步的时候吗,都选择当前看起来“最优的”解法
(3)希望得到全局最优解
2.贪心算法的特点
(1) 贪心策略的提出是没有标准以及模板的
(2) 可能每一道题的贪心策略都是不同的
(3)贪心策略的正确性:可能会出错;正确的贪心策略,我们是需要“证明的”
3.证明贪心策略的方法:数学中见过的所有证明方法
4.学习贪心的方向
(1):遇到不会的贪心题,很正常,把心态放平
(2):把策略当成经验吸收
(3):能证明则证明贪心策略的正确性
目录
- 👉🏻柠檬水找零
👉🏻柠檬水找零
原题链接:柠檬水找零
mycode:
class Solution {
public:bool lemonadeChange(vector<int>& bills) {int five = 0,ten = 0,twenty = 0;for(auto e:bills){if(e==5){five++;}else if(e==10){ten++;if(--five<0)return false;}else if(e==20){twenty++;//10+5 && 5+5+5 都不可以才找零失败int tmp1 = ten,tmp2 = five,tmp3 = five;if(--tmp1>=0&&--tmp2>=0){--ten;--five;}else if((tmp3-=3)>=0){five-=3;}elsereturn false;}}return true;}
};
交换论证法:
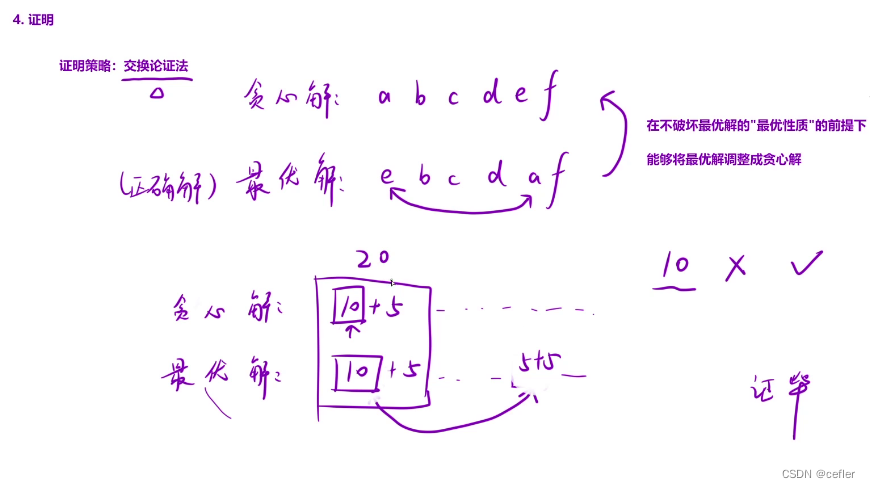
相关文章:

【贪心算法】专题练习一
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析(3) 前言 1.什么是贪心算法?——贪婪鼠目寸光 贪心策…...

【JMeter】使用nmon进行性能资源监控
一、前言 在工作中可能会遇到需要在压测的时候对Linux服务器进行性能资源监控的情况。这时可以用nmon来对服务器进行监控。 二、nmon的下载安装 1.查看系统信息 shell cat /etc/os-release 结果为 shell PRETTY_NAME"Debian GNU/Linux 12 (bookworm)" NAME&…...
Unity预设体
目录 预设体是什么? 如何创建预设体? 如何修改预设体? 如何删除预设体? 预设体是什么? Unity中的预设体(Prefab)是一种可重复使用的游戏对象模板。它允许开发者创建一个或多个游戏对象&…...

Elasticsearch 写入优化探索:是什么影响了refresh 耗时?
1、问题背景: 数据写入后,refresh耗时过长,能达到1s-5s。 想通过测试,探索确认影响refresh的因素,比如:写入操作是新增还是更新,deleted文档占比是否有影响,是否有其他索引配置&…...

Java8新特性——函数式接口
目录 一、介绍 二、示例 (一)Consumer 源码解析 测试示例 (二)Comparator (三)Predicate 三、应用 四、总结 一、介绍 FunctionalInterface是一种信息注解类型,用于指明接口类型声明…...

Epson打印机连接wifi
环境 Epson L3153 打印机联通无线光猫 背景 最近家里的联通宽带不太稳定,经常断网。今天打了联通客服电话,师傅上门来,说可能是光猫用的时间太长了,换了一个新的联通光猫,问题解决。 wifi的名称是 CU_Y3ft 和 CU_Y3…...

Chapter 7 - 6. Congestion Management in Ethernet Storage Networks以太网存储网络的拥塞管理
Dedicated and Converged Ethernet Network专用和融合以太网网络 Just because a network is configured as a converged Ethernet network (lossy and lossless traffic), doesn’t necessarily mean that lossy and lossless traffic runs on it simultaneously. For exampl…...

【论文笔记】NeuRAD: Neural Rendering for Autonomous Driving
原文链接:https://arxiv.org/abs/2311.15260 1. 引言 神经辐射场(NeRF)应用在自动驾驶中,可以创建可编辑的场景数字克隆(可自由编辑视角和场景物体),以进行仿真。但目前的方法或者需要大量的训…...

通信原理 | 分贝dB、功率、功率谱、功率谱密度、信噪比
文章目录 分贝功率和分贝的关系能量谱功率谱功率谱和功率谱密度是不同的功率谱密度随机信号和确知信号信噪比基本定义分贝表示应用分贝 分贝:(用dB表示)是量度两个相同单位之间数量比例的计量单位,主要用于度量声音强度。 1贝尔(B)=10分布(dB),即1B = 10dB 分贝是以美国…...

Go中的Context是什么?
在 Go 编程语言(通常称为 Golang)中,术语 "上下文 "指的是上下文包及其定义的上下文类型。上下文包用于跨 API 边界和进程间传输截止日期、取消信号和其他请求范围值。 上下文包的主要目的是管理并发或分布式系统中操作的生命周期…...
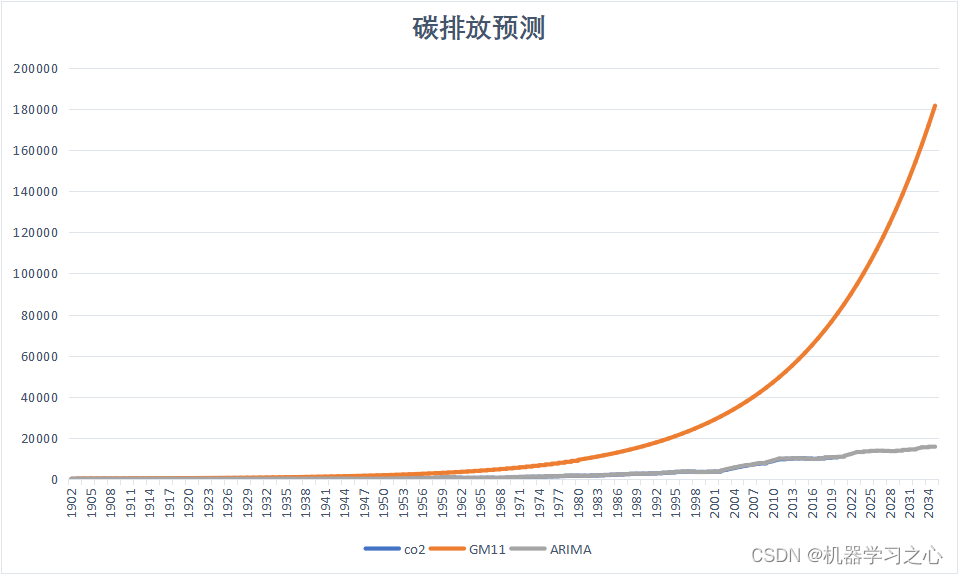
碳排放预测 | 基于ARIMA和GM(1,1)的碳排放预测(Matlab)
目录 预测效果基本介绍模型描述ARIMA模型GM(1,1)模型 程序设计参考资料 预测效果 基本介绍 基于ARIMA和GM(1,1)的碳排放预测(Matlab) 基于ARIMA(自回归移动平均模型)和GM(1,1)(灰色预测模型)的碳排放预测是…...

FPFA.一种二倍频电路代码描述以及测量详情
一、前言 1、因为需要倍频电路所以找了个二倍频的电路,通过fpga实际测量发现经过倍频后的电路峰值降低。不过这个也正常,因为该电路只要过触发点就会开始发生波形变化,而电路的触发值不是峰值。 2、继续对电路做倍频后信号做二…...
dotnet命令创建C#项目,VSCode打开
在命令行中创建项目并运行 1.首先安装.net 下载地址:.NET | 构建。测试。部署。 2.在 cmd 控制台输入 dotnet --vesion 检查版本号是否正常 3.我用git bash环境输入命令创建项目 // 创建文件夹 mkdir MyVSCode // 进入该文件夹 cd MyVSCode/ // 创建控制台项目 dotnet …...

在GitHub找开源项目
在 GitHub 的搜索框里: 使用搜索关键词可以在 GitHub 上快速的找你需要的开源项目: 限制搜索范围 通过 in 关键词 (大小写不敏感) 限制搜索范围: 公式搜索范围in:name xxx项目名包含xxxin:description xxx项目描述包含xxxin:readme xxx项目…...

GAMES101-LAB1
文章目录 一、问题简述二、框架准备三、作业参考3.1 模型矩阵3.1 参考代码 3.2 投影矩阵3.2.1 压扁操作(透视投影)3.2.2 正交投影3.2.3 参考代码 四、附件 一、问题简述 接下来的三次作业,将模拟一个基于CPU的光栅化渲染器的简化版本本次作业的任务是实现一个旋转矩…...

Docker 编译OpenHarmony 4.0 release
一、背景介绍 1.1、环境配置 编译环境:Ubuntu 20.04OpenHarmony版本:4.0 release平台设备:RK3568 OpenHarmony 3.2更新至OpenHarmony 4.0后,公司服务器无法编译通过,总是在最后几十个文件时报错,错误码4000…...

Vue 3 表单处理精讲:打造响应式注册表单的艺术
🧙♂️ 诸位好,吾乃诸葛妙计,编程界之翘楚,代码之大师。算法如流水,逻辑如棋局。 📜 吾之笔记,内含诸般技术之秘诀。吾欲以此笔记,传授编程之道,助汝解技术难题。 &…...
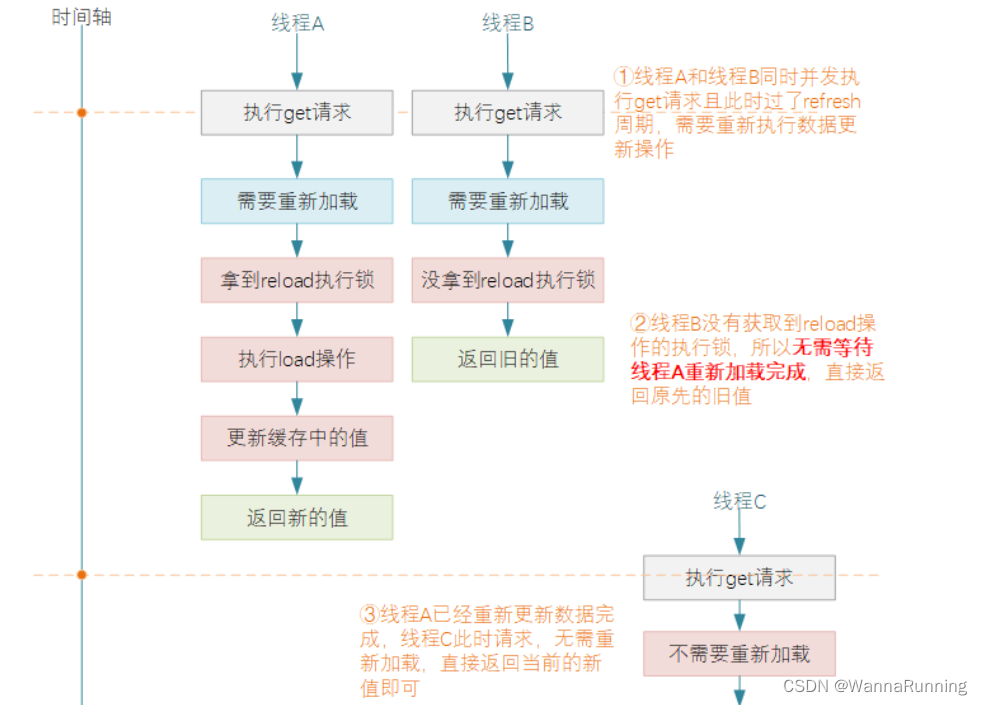
浅谈Guava Cache的参数使用
CacheLoader 用于数据加载方式比较固定且统一的场景,在缓存容器创建的时候就需要指定此具体的加载逻辑。通常开发中使用时我们需要继承CacheLoader类或写一个匿名实现类实现其load方法和reload方法 load方法 当执行get操作没有命中缓存或者判断缓存已经超出expir…...
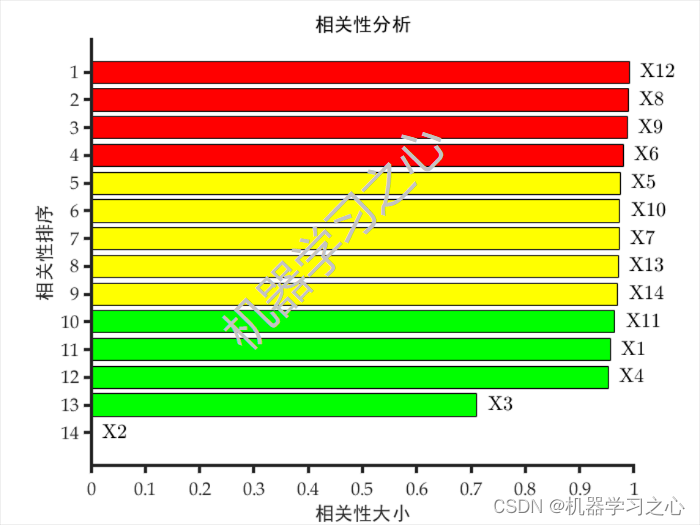
交通流预测 | Matlab基于KNN-BiLSTM的交通流预测(对比SVR、LSTM、GRU、KNN-LSTM)
目录 预测效果基本介绍程序设计参考资料 预测效果 基本介绍 交通流预测 | Matlab基于KNN-BiLSTM的交通流预测(对比SVR、LSTM、GRU、KNN-LSTM) 程序设计 完整程序和数据获取方式:私信博主回复Matlab基于KNN-BiLSTM的交通流预测(对…...
)
云卷云舒:面向业务的智能运维(上)
1、BAIOPS-业务智能运维 智能运维(AIOps-Algorithmic IT Operations基于算法的IT运维)是人工智能技术在IT运维领域的运用,引用Gartner 的报告的一段话“到2020年,将近50%的企业将会在他们的业务和IT运维方面采用AIOps,…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
