1.倒排索引 2.逻辑斯提回归算法
1.倒排索引
https://help.aliyun.com/zh/open-search/retrieval-engine-edition/introduction-to-inverted-indexes
倒排索引(Inverted Index)是一种数据结构,用于快速查找包含某个特定词或词语的文档。它主要用于全文搜索引擎等应用,允许用户根据关键词迅速定位相关文档。
倒排索引的基本思想是反转(倒排)文档-词语的映射关系。通常,在构建倒排索引时,会对文档集合中的每个文档进行分词,并记录每个词在哪些文档中出现。每个词都对应一个包含它的文档列表。这样,当需要搜索包含某个关键词的文档时,只需查找倒排索引中相应词的文档列表。
以下是构建倒排索引的基本步骤:
-
文档分词: 将每个文档进行分词,得到一组词语。
-
构建映射关系: 对每个词语,记录它在哪些文档中出现。
-
构建倒排索引: 对每个词语,建立一个索引,将其映射到包含它的文档列表。
倒排索引的优点包括:
-
高效的检索: 对于大规模文本数据,使用倒排索引可以快速定位包含特定关键词的文档。
-
省空间: 与直接存储文档之间的映射关系相比,倒排索引通常更省空间。
-
支持复杂查询: 可以轻松支持多关键词的布尔查询和短语查询等。
倒排索引在全文搜索引擎中被广泛应用,例如在Google、Bing等搜索引擎中,它们利用倒排索引实现了快速而准确的搜索功能。
2.逻辑斯提回归算法
逻辑斯蒂回归(Logistic Regression)是一种用于二分类问题的机器学习算法,尽管名字中包含“回归”一词,但它实际上是一种分类算法而非回归算法。逻辑斯蒂回归可以用于解决概率估计问题,它输出一个在0和1之间的概率值,表示样本属于某一类的可能性。
逻辑斯蒂回归的基本原理如下:

-
假设函数: 假设函数采用逻辑斯蒂(sigmoid)函数,它的数学表达式为:
[ h_\theta(x) = \frac{1}{1 + e{-\thetaT x}} ]
其中,(h_\theta(x)) 是样本 (x) 属于正类的概率,(\theta) 是模型的参数向量。
-
损失函数: 逻辑斯蒂回归使用交叉熵损失函数(Cross-Entropy Loss)来衡量模型的性能,其数学表达式为:
[ J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right] ]
其中,(m) 是样本数量,(y^{(i)}) 是样本 (x^{(i)}) 的实际类别标签。
-
参数优化: 通过最小化损失函数来优化模型的参数 (\theta)。这通常使用梯度下降等优化算法来实现。
逻辑斯蒂回归适用于线性可分的二分类问题,它对特征进行线性组合,并通过逻辑斯蒂函数将结果映射到0到1之间的概率。在实践中,逻辑斯蒂回归广泛应用于各种领域,如医学、金融和自然语言处理等。
需要注意的是,逻辑斯蒂回归虽然名字中包含“回归”,但其实质是一种分类算法,用于解决二分类问题。在处理多分类问题时,可以通过扩展为多类别逻辑斯蒂回归(Multinomial Logistic Regression)或使用其他多分类算法。
2.1 机器学习算法(一):逻辑回归模型(Logistic Regression, LR)
https://blog.csdn.net/weixin_39910711/article/details/81607386
(1) 分类平面是平面,曲面或者超平面分别是什么含义与作用
在机器学习中,分类平面、曲面和超平面是描述决策边界(decision boundary)的概念,这些边界用于将不同类别的样本分开。
-
分类平面: 一般指的是在二维空间中的平面,用于将两个类别的数据点分开。在这种情况下,决策边界就是一个平面。分类平面用于解决简单的二分类问题,其中数据可以被直线或平面分开。
-
曲面: 当决策边界不能通过平面表示,而需要通过曲面来分隔不同类别的样本时,我们可以使用曲面。曲面可以是在三维空间中的曲面,也可以是在更高维度空间中的曲面。曲面常常用于解决二分类或多分类问题。
-
超平面: 超平面是在高维空间中的一个平面。在机器学习中,支持向量机(Support Vector Machine,SVM)等算法常常使用超平面作为决策边界。对于二分类问题,超平面是一个 (n-1) 维的平面,其中 n 是特征的维度。超平面将特征空间分成两个部分,每一部分对应一个类别。
这些概念的作用是定义了模型的决策边界,即在特征空间中,模型如何将不同类别的样本分隔开。决策边界的形状取决于模型的类型和复杂性。线性模型(如逻辑斯蒂回归、线性支持向量机)可能产生线性的决策边界(平面或超平面),而非线性模型(如核支持向量机、决策树)可能产生曲面或更为复杂的决策边界,以更好地拟合数据。

(2)什么是交叉熵?什么是MSE?分别有什么优势和劣势。
交叉熵(Cross-Entropy)和均方误差(Mean Squared Error,MSE)是用于衡量模型预测值与真实值之间差异的两种损失函数。它们在不同的任务和模型中有各自的优势和劣势。
1. 交叉熵(Cross-Entropy):
交叉熵主要用于分类问题,特别是在神经网络中用作分类模型的损失函数。对于二分类问题,交叉熵损失函数的数学表达式如下:

优势:
- 适用于分类问题,尤其在深度学习中常用于训练分类模型。
- 对于分类问题,交叉熵损失函数可以更好地反映模型对不同类别的置信度。
劣势:
- 对于离散的标签,交叉熵更为适用,但在一些回归问题上不够合适。
2. 均方误差(Mean Squared Error,MSE):
均方误差主要用于回归问题,衡量模型预测值与真实值之间的平方差的平均值。均方误差的数学表达式为:

其中,(y_i) 是真实标签,(\hat{y}_i) 是模型的预测值,(N) 是样本数量。
优势:
- 适用于回归问题,对于输出是连续值的任务较为合适。
- 对异常值不敏感,因为使用了平方。
劣势:
- 在处理分类问题时,MSE 通常不如交叉熵效果好,因为它对于分类问题中的概率分布不够敏感。
在选择损失函数时,需要根据任务类型和模型特性进行合适的选择。在分类任务中,通常使用交叉熵损失函数;而在回归任务中,可以选择均方误差或其他适用的回归损失函数。
2.2 【机器学习】逻辑回归(非常详细)
https://zhuanlan.zhihu.com/p/74874291
2.3 加入正则化项的作用,以及加入正则化项的形式
正则化是在机器学习模型的训练过程中为损失函数添加额外项,以避免过拟合和提高模型的泛化能力。通过正则化,可以对模型参数的大小进行限制,防止其过于复杂,减小模型对训练数据的过度拟合。
在损失函数中添加正则化项的一般形式为:

其中,(J(\theta)) 是包含正则化项的新损失函数,(\lambda) 是正则化强度的超参数,(\theta) 是模型的参数。
常用的正则化项包括 L1 正则化和 L2 正则化:

L2 正则化通过对权重的平方进行惩罚,倾向于让权重尽可能小,但不会让它们变为零。它有助于缓解特征间的共线性问题。
在机器学习中,正则化的作用有以下几点:
-
防止过拟合: 正则化通过限制模型的复杂度,防止模型在训练数据上过度拟合,提高对新数据的泛化能力。
-
特征选择: L1 正则化的特点是可以使一些特征的权重为零,从而实现特征选择,减少不重要的特征对模型的影响。
-
缓解共线性: L2 正则化有助于缓解特征之间的共线性问题,使模型对输入特征变化更为稳健。
在实际应用中,超参数 (\lambda) 的选择通常通过交叉验证等方法来确定。正则化在许多机器学习算法中都得到了广泛的应用,例如线性回归、逻辑斯蒂回归、支持向量机等。
2.4 为什么L1正则化可以产生稀疏模型(L1是怎么让系数等于零的),以及为什么L2正则化可以防止过拟合。
L1 正则化产生稀疏模型的原因:
L1 正则化通过在损失函数中添加 ( \lambda \sum_{i=1}^{n} |w_i| ) 项,其中 (w_i) 是模型的权重,(n) 是权重的数量。这个额外的惩罚项具有一种特殊的性质,它促使模型学习到的权重中的一些值变为零。

具体来说,L1 正则化在优化过程中,倾向于将某些特征对应的权重直接设为零。这是因为 L1 正则化的梯度在某个特征的权重等于零时不可导,而在其他地方都是可导的。因此,为了最小化损失函数,模型倾向于让一些特征的权重直接变为零,从而实现稀疏性。
对于具有大量特征的问题,L1 正则化能够帮助识别并保留对目标变量预测有贡献的关键特征,而将其他特征的权重设为零。这种特性在特征选择和解释模型中很有用。
L2 正则化防止过拟合的原因:
L2 正则化通过在损失函数中添加 ( \lambda \sum_{i=1}^{n} w_i^2 ) 项,其中 (w_i) 是模型的权重,(n) 是权重的数量。相比于 L1 正则化,L2 正则化的梯度在任何地方都是可导的。

L2 正则化的效果主要表现在对权重的平方进行惩罚。这导致模型在训练过程中倾向于将权重保持较小的值,避免过度拟合训练数据。
防止过拟合的原因在于,L2 正则化通过限制权重的大小,减缓了模型对训练数据中噪声的过度拟合。较小的权重值使得模型对输入特征的小变化不敏感,从而提高了模型对新数据的泛化能力。
综合来看,L1 正则化通过产生稀疏模型,有助于特征选择和模型解释;而 L2 正则化通过控制权重的大小,有助于防止模型过拟合。在实际应用中,可以根据问题的特性选择使用 L1 正则化、L2 正则化,或者它们的组合(弹性网络 Elastic Net)。
2.5 softmax函数
Softmax 函数是一种常用的激活函数,特别适用于多分类问题。它将一个包含任意实数的 K 维向量,映射为一个 K 维的概率分布,其中每个元素的取值范围在 (0, 1) 之间,并且所有元素的和为 1。

Softmax 函数的性质使得它在多分类问题中特别有用,因为它可以将模型的原始输出转换为类别概率。在深度学习中,通常将 Softmax 函数作为神经网络输出层的激活函数,以便将神经网络的原始输出转换为类别概率。
Softmax 函数的特点包括:
-
归一性: Softmax 函数的输出是一个概率分布,因此所有元素的和等于 1,这使得它可以表示一个完整的类别分布。
-
连续性: Softmax 函数是光滑的,可导数的,这在梯度下降等优化算法中很有用。
-
转换作用: Softmax 函数对原始分数进行了指数变换,使得大的分数更大,小的分数更小,这有助于突显模型在输入上的置信度。
Softmax 函数在交叉熵损失(Cross-Entropy Loss)等多分类问题中的配合使用,使得模型能够输出概率分布,并且在训练过程中通过最小化损失函数来调整模型参数,以便更好地匹配真实的类别分布。
5 为什么逻辑斯蒂回归的输出值可以作为概率
逻辑斯蒂回归(Logistic Regression)的输出值可以被解释为样本属于某一类别的概率,这是因为逻辑斯蒂回归使用了逻辑斯蒂函数(sigmoid函数)作为激活函数。
逻辑斯蒂函数的数学表达式为:

逻辑斯蒂函数具有以下性质:
-
输出范围:逻辑斯蒂函数的输出范围在 (0, 1) 之间,即对于任何实数输入,输出都在 0 到 1 之间。
-
单调性:逻辑斯蒂函数是单调递增的,即当 (z_1 < z_2) 时,(\sigma(z_1) < \sigma(z_2))。
-
饱和性:逻辑斯蒂函数在两端接近 0 或 1,但不会完全到达,因此避免了输出值严格等于 0 或 1。
由于逻辑斯蒂函数的输出在 (0, 1) 之间,并且趋向于0或1,可以将其解释为某个样本属于正类别的概率。在二分类问题中,通常设定一个阈值(例如0.5),当逻辑斯蒂函数的输出大于阈值时,将样本划分为正类别,否则划分为负类别。
这种概率的解释使得逻辑斯蒂回归在分类问题中非常有用,尤其是在需要估计概率而不仅仅是类别标签的情况下。逻辑斯蒂回归的训练过程通过最小化对数损失函数,使得模型输出的概率尽量接近真实标签的概率。
相关文章:

1.倒排索引 2.逻辑斯提回归算法
1.倒排索引 https://help.aliyun.com/zh/open-search/retrieval-engine-edition/introduction-to-inverted-indexes 倒排索引(Inverted Index)是一种数据结构,用于快速查找包含某个特定词或词语的文档。它主要用于全文搜索引擎等应用&#…...
Kafka消费者组
消费者总体工作流程 Consumer Group(CG):消费者组,由多个consumer组成。形成一个消费者组的条件,是所有消费者的groupid相同。 • 消费者组内每个消费者负责消费不同分区的数据,一个分区只能由一个组内消费…...

四. 基于环视Camera的BEV感知算法-BEVDepth
目录 前言0. 简述1. 算法动机&开创性思路2. 主体结构3. 损失函数4. 性能对比总结下载链接参考 前言 自动驾驶之心推出的《国内首个BVE感知全栈系列学习教程》,链接。记录下个人学习笔记,仅供自己参考 本次课程我们来学习下课程第四章——基于环视Cam…...
——使用docker compose安装mysql)
CentOS系统环境搭建(二十五)——使用docker compose安装mysql
centos系统环境搭建专栏🔗点击跳转 文章目录 使用docker compose安装mysqlMySQL81.新建文件夹2.创建docker-compose.yaml3.创建my.cnf4.mysql容器的启动和关闭 MySQL5.71.新建文件夹2.创建docker-compose.yaml3.创建my.cnf4.mysql容器的启动和关闭 使用docker comp…...
协作机器人(Collaborative-Robot)安全碰撞的速度与接触力
协作机器人(Collaborative-Robot)的安全碰撞速度和接触力是一个非常重要的安全指标。在设计和使用协作机器人时,必须确保其与人类或其他物体的碰撞不会对人员造成伤害。 对于协作机器人的安全碰撞速度,一般会设定一个上限值&…...

第11章 GUI Page400~402 步骤二 画直线
运行效果: 源代码: /**************************************************************** Name: wxMyPainterApp.h* Purpose: Defines Application Class* Author: yanzhenxi (3065598272qq.com)* Created: 2023-12-21* Copyright: yanzhen…...

华为gre隧道全部跑静态路由
最终实现: 1、pc1能用nat上网ping能pc3 2、pc1能通过gre访问pc2 3、全部用静态路由做,没有用ospf,如果要用ospf,那么两边除了路由器上跑ospf,核心交换机也得用ospf r2配置: acl number 3000 rule 5 deny…...

【c++】入门1
c关键字 命名空间 在C/C中,变量、函数和后面要学到的类都是大量存在的,这些变量、函数和类的名称将都存在于全局作用域中,可能会导致很多冲突。使用命名空间的目的是对标识符的名称进行本地化,以避免命名冲突或名字污染ÿ…...
Python之Django项目的功能配置
1.创建Django项目 进入项目管理目录,比如:D盘 执行命令:diango-admin startproject demo1 创建项目 如果提示diango命令不存在,搜索diango-admin程序的位置,然后加入到环境变量path中。 进入项目,cd demo…...
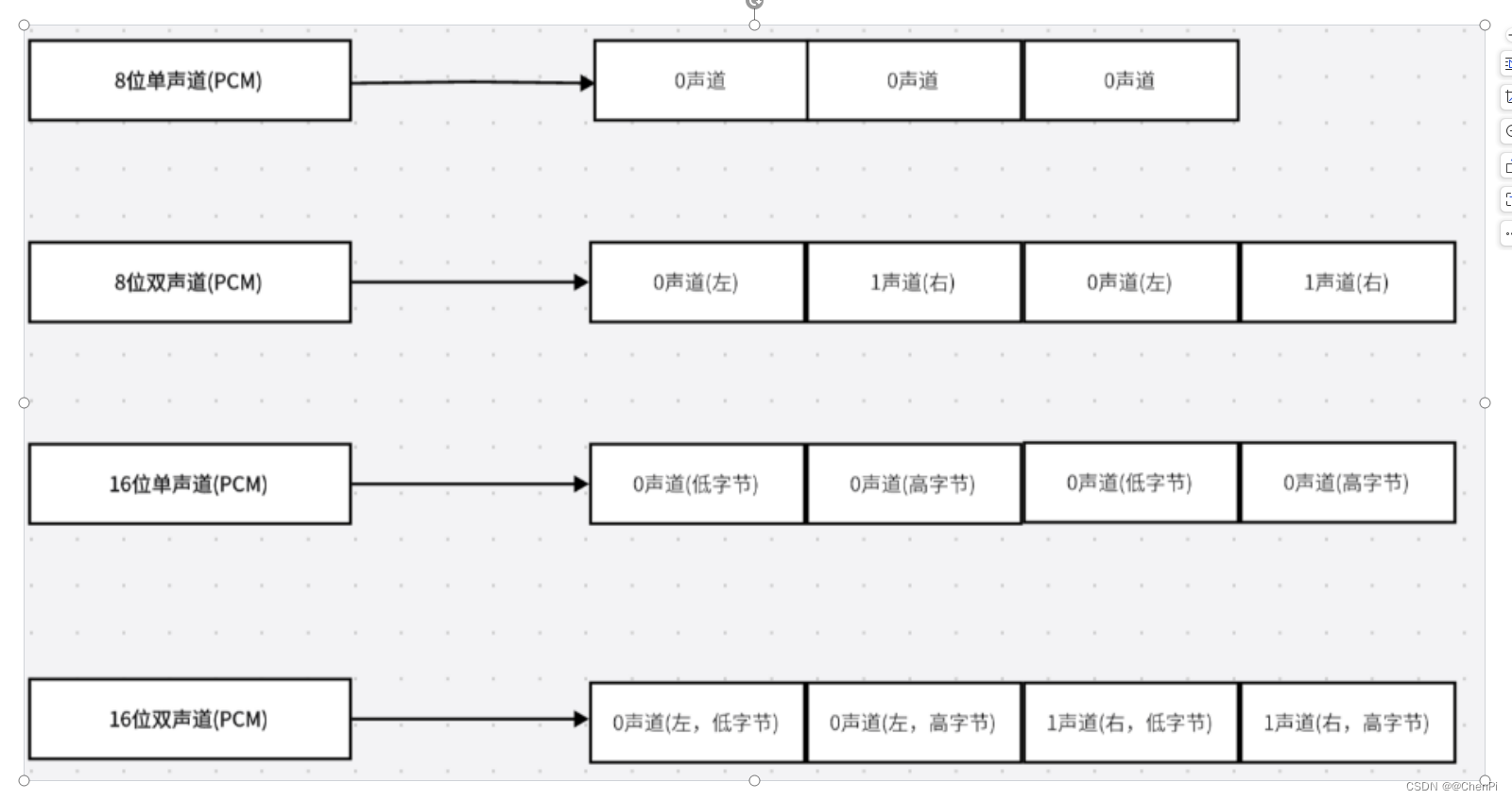
P4 音频知识点——PCM音频原始数据
目录 前言 01 PCM音频原始数据 1.1 频率 1.2 振幅: 1.3 比特率 1.4 采样 1.5 量化 1.6 编码 02. PCM数据有以下重要的参数: 采样率: 采集深度 通道数 PCM比特率 PCM文件大小计算: …...

解决Electron中WebView加载部分HTTPS页面白屏的方法
Electron是一个开源的桌面应用程序框架,它允许使用Web技术构建跨平台的桌面应用。在Electron应用中,WebView 是一个常用的组件,用于嵌套加载Web内容。然而,有时候在加载使用 HTTPS 协议的页面时,可能会因为证书问题导致…...

【Java中创建对象的方式有哪些?】
✅Java中创建对象的方式有哪些? ✅使用New关键字✅使用反射机制✅使用clone方法✅使用反序列化✅使用方法句柄✅ 使用Unsafe分配内存 ✅使用New关键字 这是我们最常见的也是最简单的创建对象的方式,通过这种方式我们还可以调用任意的构造函数 (无参的和有…...
)
npm使用详解(好吧好吧是粗解)
目录 npm是什么? npm有什么用? npm安装 在 Windows 上 在 macOS 上 在 Linux 上(使用 apt 包管理器为例) 验证 npm 安装成功: npm使用 1. 初始化项目: 2. 安装和管理依赖: 3. 查看和…...
uniapp自定义头部导航怎么实现?
一、在pages.json文件里边写上自定义属性 "navigationStyle": "custom" 二、在对应的index页面写上以下: <view :style"{ height: headheight px, backgroundColor: #24B7FF, zIndex: 99, position: fixed, top: 0px, width: 100% …...
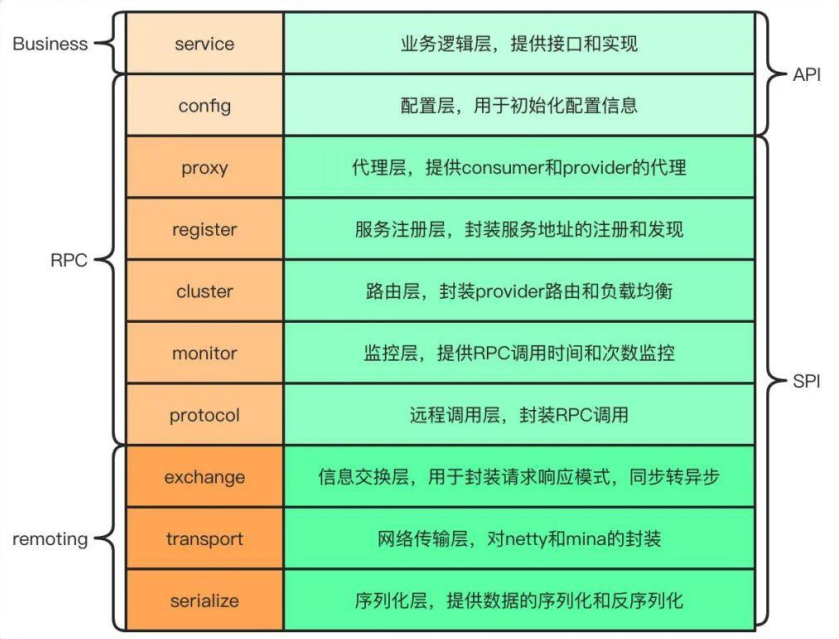
什么是 Dubbo?它有哪些核心功能?
文章目录 什么是 Dubbo?它有哪些核心功能? 什么是 Dubbo?它有哪些核心功能? Dubbo 是一款高性能、轻量级的开源 RPC 框架。由 10 层模式构成,整个分层依赖由上至下。 通过这张图我们也可以将 Dubbo 理解为三层模式&…...
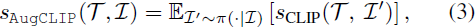
(2021|CoRR,AugCLIP,优化)FuseDream:通过改进的 CLIP+GAN 空间优化实现免训练文本到图像生成
FuseDream: Training-Free Text-to-Image Generation with Improved CLIPGAN Space Optimization 公众:EDPJ(添加 VX:CV_EDPJ 或直接进 Q 交流群:922230617 获取资料) 目录 0. 摘要 1. 简介 2. CLIPGAN 文本到图…...

python pip安装依赖的常用软件源
目录 引言 一、什么是镜像源? 二、清华源 三、阿里源 四、中科大源 五、豆瓣源 六、更多资源 引言 在软件开发和使用过程中,我们经常需要下载和更新各种软件包和库文件。然而,由于网络环境的限制或者服务器的负载&#…...

避免大M取值过大引起的数值问题
在数学建模当中,常常会见到大M法,它之所以叫大M法,是因为它涉及到一个(绝对值)较大的系数M,这个大M的值应大于约束中的连续变量或者约束表达式可能取到的任何合理值,M值取过大往往会造成优化问题…...

史密斯圆图的使用
史密斯圆图的使用 简介识别史密斯圆图等反射系数圆归一化阻抗圆导纳圆图史密斯圆图的使用单支匹配双支匹配简介 史密斯图Smith Chart是电气工程,无线电,射频工程,微波工程和通信等领域常用的一种图示工具,用于分析和设计传输线和阻抗匹配网络,它由美国工程师Phillip H.Sm…...

可重复读解决了哪些问题? 对 SQL 慢查询会考虑哪些优化 ?
文章目录 可重复读解决了哪些问题?对 SQL 慢查询会考虑哪些优化 ? 可重复读解决了哪些问题? (1)可重复读的核心就是一致性读(consistent read);保证多次读取同一个数据时,其值都和事务开始时候的内容是一致…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...
