算法通关村-番外篇排序算法
大家好我是苏麟 , 今天带来番外篇 .
冒泡排序 BubbleSort
最基本的排序算法,最常用的排序算法 .
我们以关键字序列{26,53,48,11,13,48,32,15}看一下排序过程:
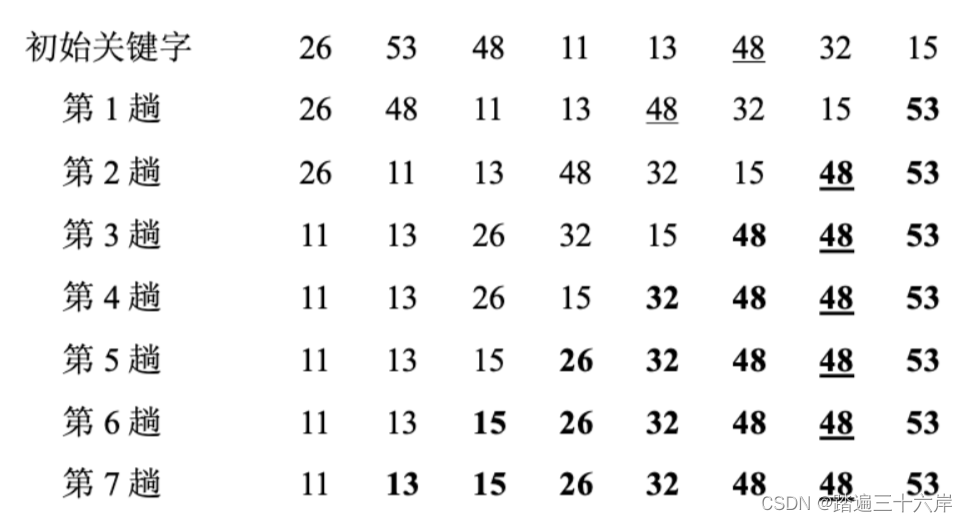
动画演示 :
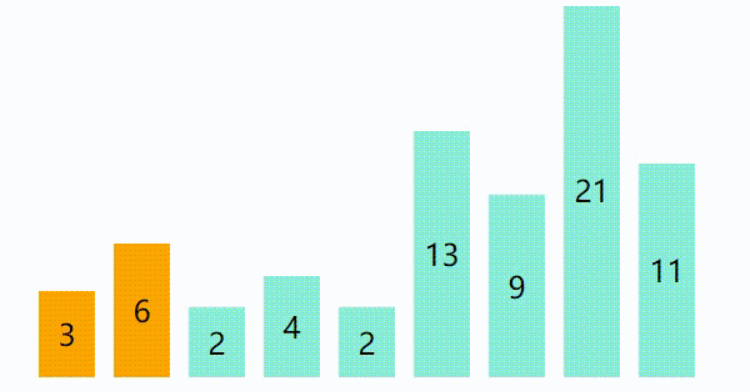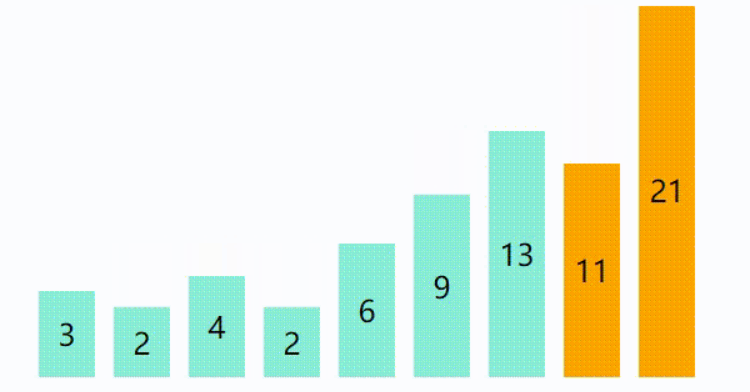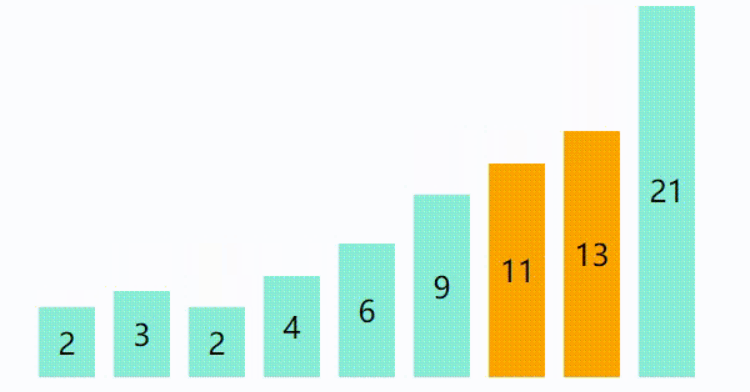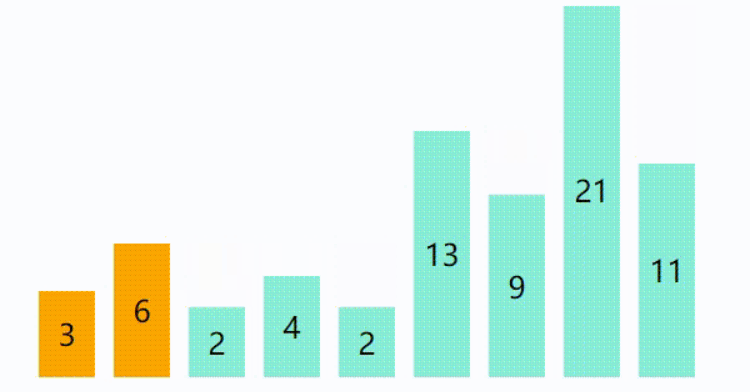
代码如下 : (基础版)
class Solution {public int[] sortArray(int[] nums) {for(int i = 0;i < nums.length - 1;i++){for(int j = 0;j < nums.length - i - 1;j++){if(nums[j] > nums[j + 1]){int temp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = temp;}}}return nums;}
}优化 :
class Solution {public int[] sortArray(int[] nums) {int flag = 1;for(int i = 0;flag && i < nums.length - 1;i++){flag = 0;for(int j = 0;j < nums.length - i - 1;j++){if(nums[j] > nums[j + 1]){int temp = nums[j];nums[j] = nums[j + 1];nums[j + 1] = temp;flag = 1;}}}return nums;}
}空间复杂度 仅仅使用一个辅助单元 ,因此空间复杂度为O(1)。
时间复杂度 假设待排序的元素个数为n,则总共需要进行n-1趟排序,对 j 个元素的子序列进行一趟排序需要进行j-1次关键字比较,因此总的比较次数为n(n-1)/2,因此时间复杂度为O(n^2)。
稳定性 冒泡排序的特点是稳定性好,因为排序过程中始终只交换相邻元素,比较对象大小相等时不交换,相对位置不变,故稳定。
选择排序 SelectSort
选择排序是默认前面都是已经排序好的,然后从后面 选择最小的放在前面排序好的的后面,首先第一轮循环的时候默认的排序好的为空,然后从后面选择最小的放到数组的第一个位置,第二轮循环的时候默认第个元素是已经 排序好的,然后从剩下的找出最小的放到数组的第二个位置,第三轮循环的时候默认前 两个都是已经排序好的,然后再从剩下的选择一个最小的放到数组的第三个位置,以此 类推。还是上面的序列,我们看一下选择排序是怎么做的:
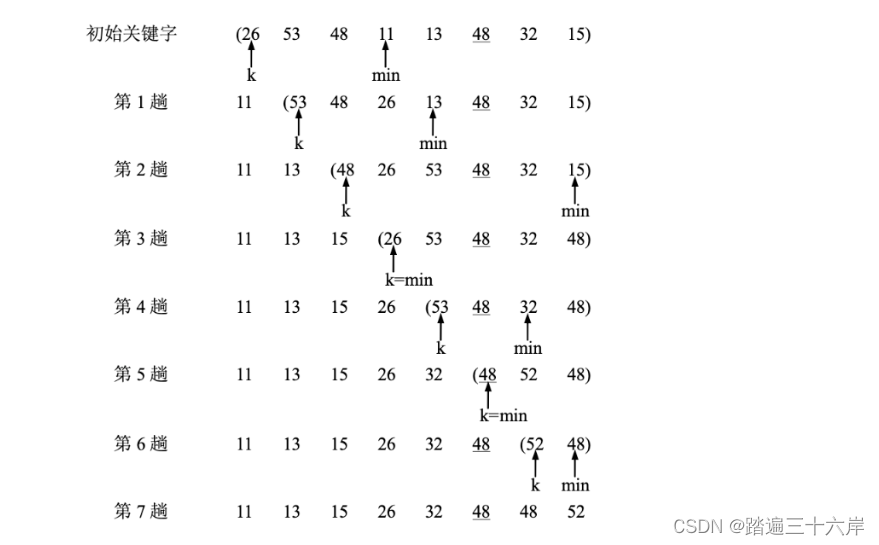
动画演示 :
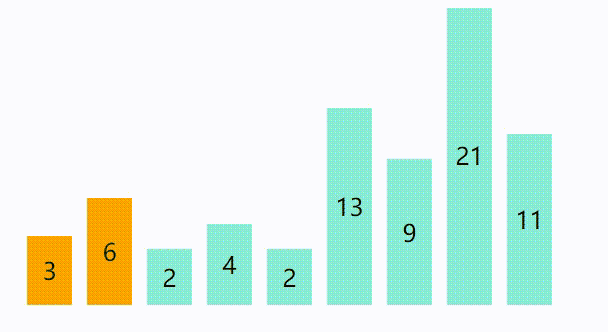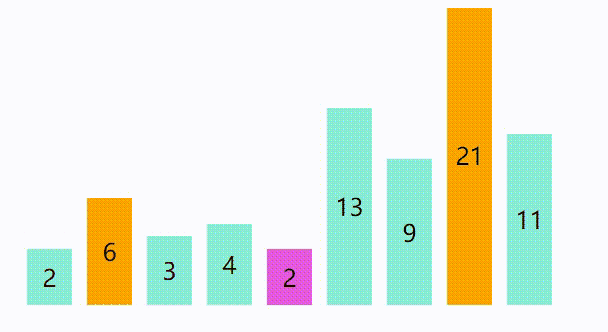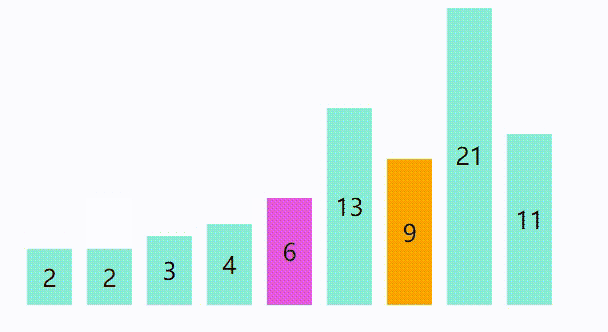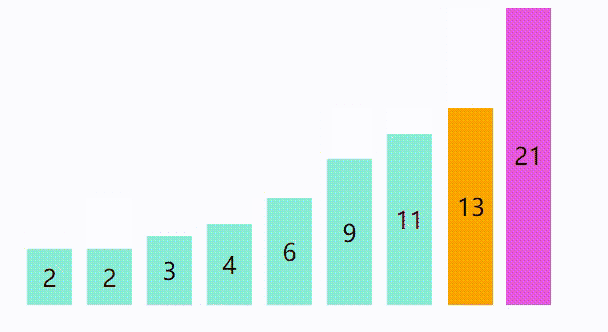
代码 :
public static void SelectSort(int[] nums){int min;for (int i = 0;i < nums.length;i++){min = i;for (int j = i + 1;j < nums.length;j++){if (nums[i] > nums[j]){min = j;}}if (i != min){int temp = nums[i];nums[i] = nums[min];nums[min] = temp;}}}空间复杂度:仅仅使用一个辅助单元 ,因此空间复杂度为O(1)
平均时间复杂度: 在待排序序列已经有序的情况下,简单选择排序不用移动元素。最坏情况下,也就是序列正好是逆序的,则要进行n(n-1)/2次比较,因此最坏时间复杂度为O(n^2).
稳定性:选择排序是不稳定算法
这期就到这里 , 下期见!
相关文章:

算法通关村-番外篇排序算法
大家好我是苏麟 , 今天带来番外篇 . 冒泡排序 BubbleSort 最基本的排序算法,最常用的排序算法 . 我们以关键字序列{26,53,48,11,13,48,32,15}看一下排序过程: 动画演示 : 代码如下 : (基础版) class Solution {public int[] sortArray(int[] nums) {for(int i …...

三种方式简单搭建http本地文件服务
有时候想写一个简单的html文件,然后加上一些image、js、css文件用于测试。希望有一个简单的http服务,总结了如下三种方式,欢迎讨论更多高效的方式。 (一)使用Web Server for Chrome浏览器扩展 之前写过一篇博文&#x…...

设计模式--适配器模式
实验8:适配器模式 本次实验属于模仿型实验,通过本次实验学生将掌握以下内容: 1、理解适配器模式的动机,掌握该模式的结构; 2、能够利用适配器模式解决实际问题。 [实验任务]:双向适配器 实现一个双向…...

Node.js教程-express框架
概述 Express是基于Node.js平台(建立在Node.js内置的http模块上),快速、开放、极简的Web开发框架。 中文官网 http://www.expressjs.com.cn/。 Github地址:https://github.com/orgs/expressjs。 Express核心特性: 可设置中间件来响应 HTTP…...

location.origin兼容
if (!window.location.origin) {window.location.origin window.location.protocol "//" window.location.hostname (window.location.port ? : window.location.port: );}...
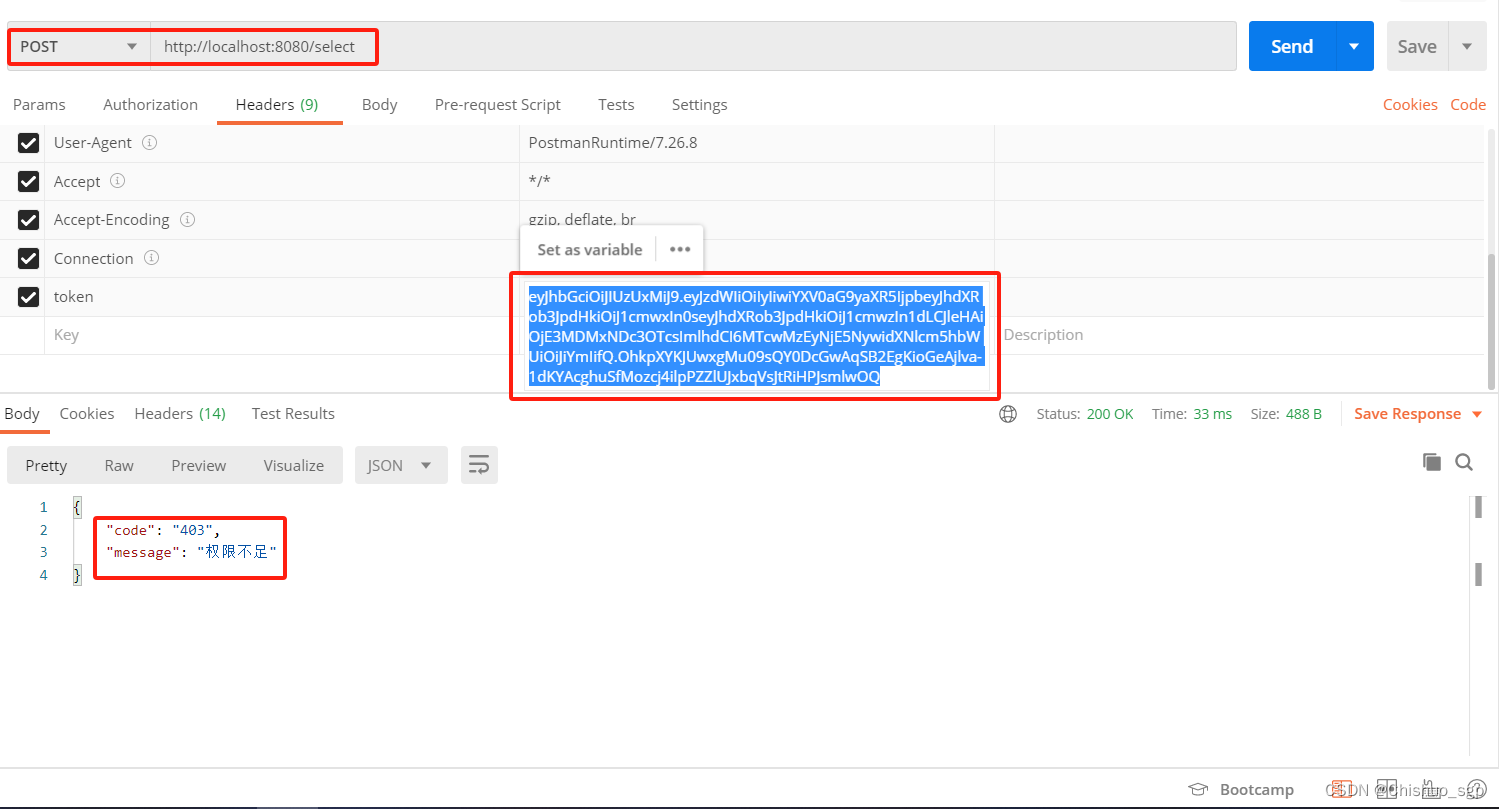
spring boot集成mybatis和springsecurity实现权限控制功能
上一篇已经实现了登录认证功能,这一篇继续实现权限控制功能,文中代码只贴出来和上一篇不一样的修改的地方,完整代码可结合上一篇一起整理spring boot集成mybatis和springsecurity实现登录认证功能-CSDN博客 数据库建表 权限控制的意思就是根…...

按键修饰符
在键盘监听事件时,我们经常需要判断详细的按键,此时,可以为键盘相关的事件添加按键修饰符,例如: 键盘修饰符案例:...
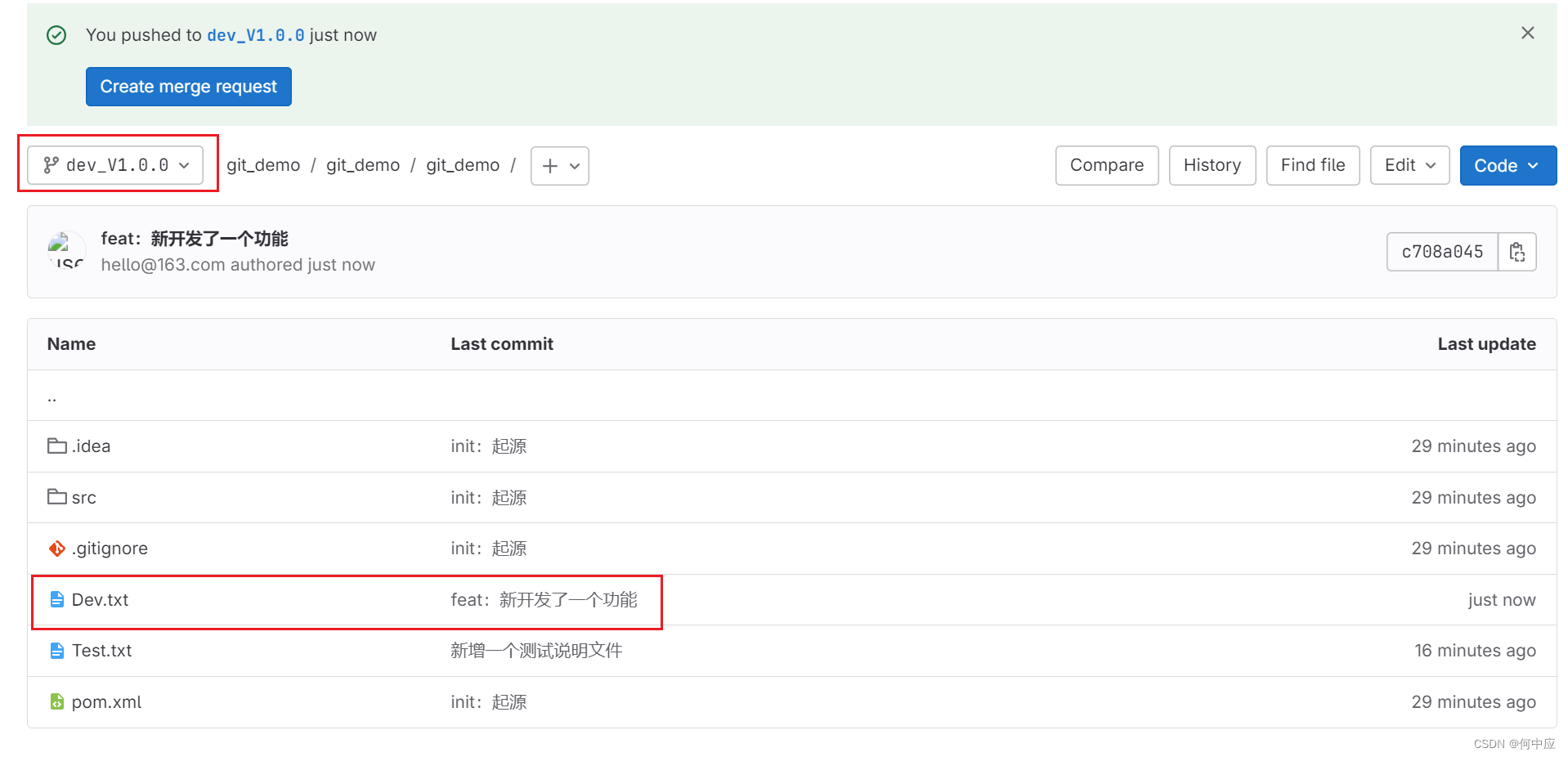
新版IDEA中Git的使用(一)
说明:本文介绍如何在新版IDEA中使用Git 创建项目 首先,在GitLab里面创建一个项目(git_demo),克隆到桌面上。 然后在IDEA中创建一个项目,项目路径放在这个Git文件夹里面。 Git界面 当前分支&Commit …...

【性能测试】真实企业,性能测试流程总结分析(一)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 性能测试什么时候…...
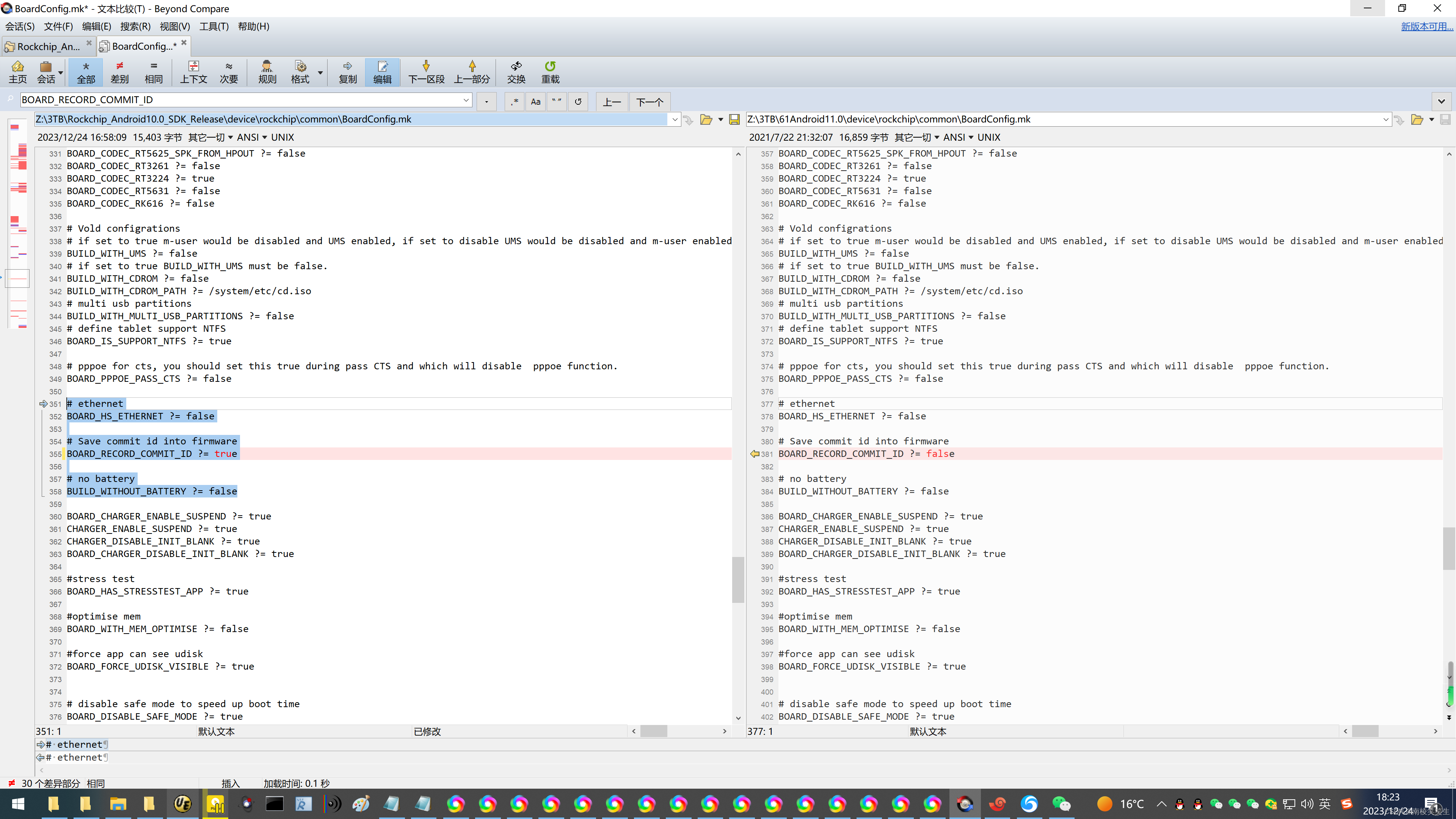
20231224解决outcommit_id.xml1 parser error Document is empty的问题
20231224解决outcommit_id.xml1 parser error Document is empty的问题 2023/12/24 18:13 在开发RK3399的Android10的时候,出现:rootrootrootroot-X99-Turbo:~/3TB/Rockchip_Android10.0_SDK_Release$ make installclean PLATFORM_VERSION_CODENAMEREL…...

电子电器架构刷写方案——General Flash Bootloader
电子电器架构刷写方案——General Flash Bootloader 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 注:文章1万字左右,深度思考者入!!! 老规矩,分享一段喜欢的文字,避免…...

【Linux】僵尸与孤儿 进程等待
目录 一,僵尸进程 1,僵尸进程 2,僵尸进程的危害 二,孤儿进程 1,孤儿进程 三,进程等待 1,进程等待的必要性 2,wait 方法 3,waitpid 方法 4,回收小结…...
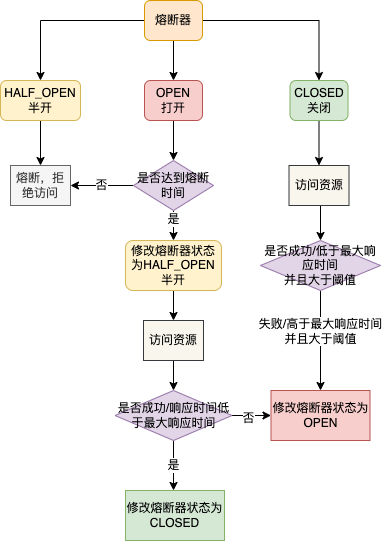
Java小案例-Sentinel的实现原理
前言 Sentinel是阿里开源的一款面向分布式、多语言异构化服务架构的流量治理组件。 主要以流量为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自适应过载保护、热点流量防护等多个维度来帮助开发者保障微服务的稳定性。 核心概念 要想理解一个新的技…...

【Leetcode Sheet】Weekly Practice 21
Leetcode Test 1901 寻找峰值Ⅱ(12.19) 一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。 给你一个 从 0 开始编号 的 m x n 矩阵 mat ,其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。 …...

C语言使用qsort和bsearch实现二分查找
引言 在计算机科学领域,查找是一项基本操作,而二分查找是一种高效的查找算法。本博客将详细解释一个简单的C语言程序,演示如何使用标准库函数qsort和bsearch来对一个整数数组进行排序和二分查找。 代码解析 包含头文件 #include <stdi…...

MySQL的替换函数及补全函数的使用
前提: mysql的版本是8.0以下的。不支持树形结构递归查询的。但是,又想实现树形结构的一种思路 提示:如果使用的是MySQL8.0及其以上的,想要实现树形结构,请参考:MySQL数据库中,如何实现递归查询…...

2022第十二届PostgreSQL中国技术大会-核心PPT资料下载
一、峰会简介 本次大会以“突破•进化•共赢 —— 安全可靠,共建与机遇”为主题,助力中国数据库基础软件可掌控、可研究、可发展、可生产,并推动数据库生态的繁荣与发展。大会为数据库从业者、数据库相关企业、数据库行业及整个IT产业带来崭…...

2024 年 10大 AI 趋势
2025 年,全球人工智能市场预计将达到惊人的 1906.1 亿美元,年复合增长率高达 36.62%。 人工智能软件正在迅速改变我们的世界,而且这种趋势在未来几年只会加速。 我们分析了未来有望彻底改变 2024 年的 10 个AI趋势。从生成式人工智能的兴起到…...

Uboot
什么是Bootloader? Linux系统要启动就必须需要一个 bootloader程序,也就说芯片上电以后先运行一段bootloader程序。 这段 **bootloader程序会先初始化时钟,看门狗,中断,SDRAM,等外设,然后将 Linux内核从f…...

ECMAScript 的未来:预测 JavaScript 创新的下一个浪潮
以下是简单概括关于JavaScript知识点以及一些目前比较流行的比如:es6 想要系统学习: 大家有关于JavaScript知识点不知道可以去 🎉博客主页:阿猫的故乡 🎉系列专栏:JavaScript专题栏 🎉ajax专栏&…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...

vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能
vxe-table vue 表格复选框多选数据,实现快捷键 Shift 批量选择功能 查看官网:https://vxetable.cn 效果 代码 通过 checkbox-config.isShift 启用批量选中,启用后按住快捷键和鼠标批量选取 <template><div><vxe-grid v-bind"gri…...

Android Framework预装traceroute执行文件到system/bin下
文章目录 Android SDK中寻找traceroute代码内置traceroute到SDK中traceroute参数说明-I 参数(使用 ICMP Echo 请求)-T 参数(使用 TCP SYN 包) 相关文章 Android SDK中寻找traceroute代码 设备使用的是Android 11,在/s…...

WinUI3开发_使用mica效果
简介 Mica(云母)是Windows10/11上的一种现代化效果,是Windows10/11上所使用的Fluent Design(设计语言)里的一个效果,Windows10/11上所使用的Fluent Design皆旨在于打造一个人类、通用和真正感觉与 Windows 一样的设计。 WinUI3就是Windows10/11上的一个…...
