C语言数据结构-----常用七种排序介绍、分类、实现及性能比较
前言
①排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
②稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
③内部排序:数据元素全部放在内存中的排序。
④外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
文章目录
- 前言
- 1.冒泡排序
- 2.插入排序
- 3.希尔排序
- 4.直接选择排序
- 5.堆排序
- 6.快速排序(qsort)
- 6.1 hoare法
- 6.2 前后指针法
- 6.3 挖洞法
- 7.归并排序
- 8.排序性能比较
1.冒泡排序
冒泡排序是我们刚接触C语言时就经常使用的排序,大家应该都清楚什么时冒泡排序,这里就不做介绍。

void BubbleSort(int* a, int n)
{for (int i = 0; i < n; i++){bool exchange = false;for (int j = 1; j < n - i; j++){if (a[j - 1] > a[j]){int temp;temp = a[j - 1];a[j - 1] = a[j];a[j] = temp;exchange = true;}}if (exchange == false)break;}
}
2.插入排序
直接插入排序是一种简单的插入排序法,其基本思想是:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。

直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}elsebreak;}a[end + 1] = tmp;}
}
3.希尔排序
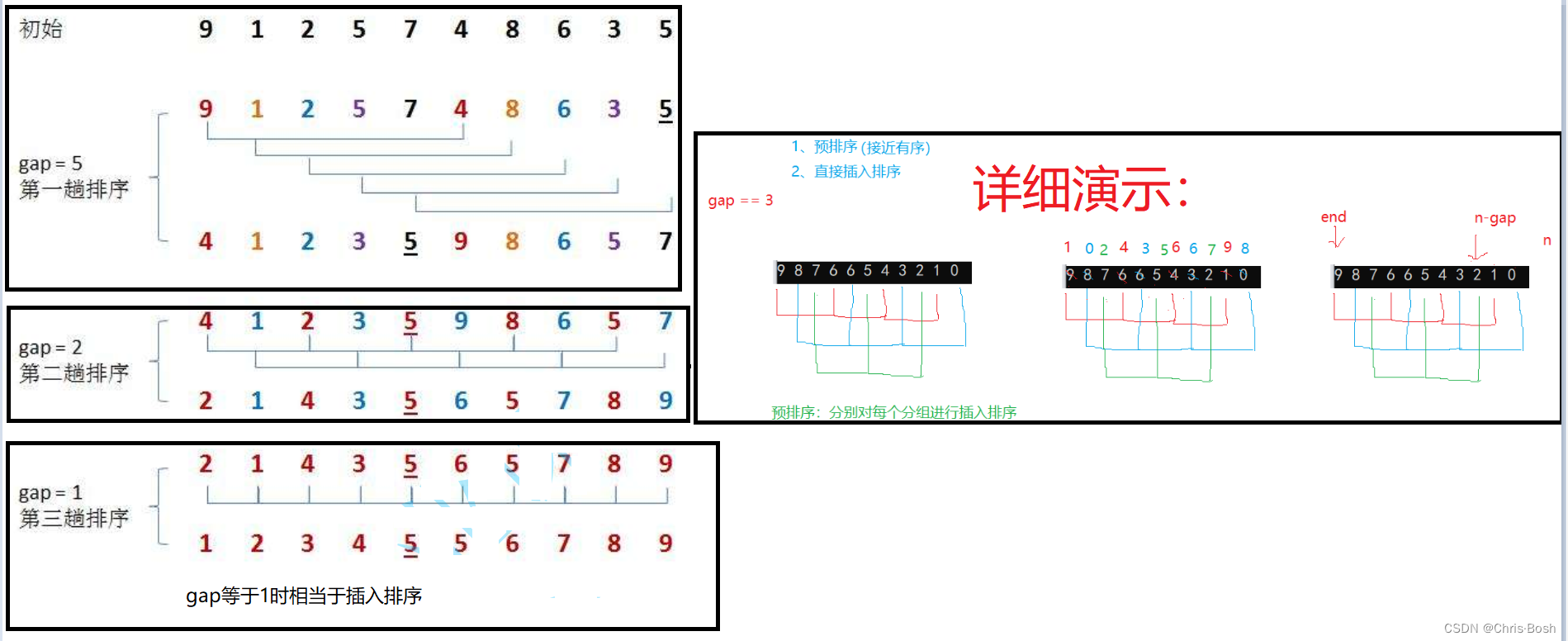
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
总结一下,步骤就是两步:
1.预排序
2.插入排序
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定。
- 研究表明希尔排序的时间复杂度约为O(N1.3)
void ShellSort(int* a, int n)
{int gap = n;// gap > 1时是预排序,目的让他接近有序// gap == 1是直接插入排序,目的是让他有序while (gap > 1){//gap = gap / 2;gap = gap / 3 + 1;//现希尔排序的常用的两种gap取值for (int i = 0; i < n - gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = tmp;}}
}
4.直接选择排序
其思想是: 每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完 。
直接选择排序的特性总结:
- 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
- 稳定性:不稳定
void SelectSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = begin;for (int i = begin + 1; i <= end; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);if (maxi == begin){maxi = mini;}Swap(&a[end], &a[maxi]);++begin;--end;}
}
5.堆排序
具体见:
链接: C语言数据结构-----二叉树(2)堆的深入理解及应用、链式二叉树的讲解及代码实现
void AdjustDown(int* a, int size, int parent)
{int child = parent * 2 + 1;while (child < size){// 假设左孩子小,如果解设错了,更新一下if (child + 1 < size && a[child + 1] > a[child]){++child;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}// 升序
void HeapSort(int* a, int n)
{// O(N)// 建大堆for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}// O(N*logN)int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}
6.快速排序(qsort)
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
其也就是我们在C语言中常使用的qsort函数。
其有三种三种版本,hoare版本,挖坑法版本,前后指针版本。让我们一种一种来看。
6.1 hoare法
用一个形象生动的动画来说明一下此方法

再配上一个简单的说明:
①先以6为基准,然后慢慢走Lift和Right。最后比基准小的在左边,比基准大的在右边。
②Right先走,走到比基准小的值就停下,然后Left走,走到比基准大的值就停下,然后交换Left和Right的值。
③然后Right继续走,走到比基准小的值就停下,然后Left走,走到比基准大的值就停下,然后继续交换。
④Right和Left相遇了,就把基准值与相遇位置的值交换。便完成了比基准小的在左边,比基准大的在右边的操作。
int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin midi end 三个数选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else // a[begin] > a[midi]{if (a[midi] > a[end])return midi;else if (a[begin] < a[end])return begin;elsereturn end;}
}void hoare_QuickSort(int* a, int begin, int end)
{if (begin >= end)return;if (end - begin + 1 <= 10){InsertSort(a + begin, end - begin + 1);}else{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin, keyi-1] keyi [keyi+1, end]hoare_QuickSort(a, begin, keyi - 1);hoare_QuickSort(a, keyi + 1, end);}
}
6.2 前后指针法
用一个形象生动的动画来说明一下此方法

配上一个简短的说明:
①以6为基准值,前驱指针prev先走,cur再走。当cur的值大于基准值时,prev不动,cur继续走,当cur的值小于基准值时,cur不动。此时,prev向前走,交换cur与prev的值。这样小的数就到前面,大的数就到后面了。
②cur继续走,以此类推。cur遇到比基准大的数就继续走,知道遇到比基准小的数,prev才动,然后交换。
③继续上述步骤,直到cur越界,然后交换基准值和prev的值。
int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin midi end 三个数选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else // a[begin] > a[midi]{if (a[midi] > a[end])return midi;else if (a[begin] < a[end])return begin;elsereturn end;}
}void point_QuickSort(int* a, int begin, int end)
{if (begin >= end)return;if (end - begin + 1 <= 10){InsertSort(a + begin, end - begin + 1);}else{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int keyi = begin;int prev = begin;int cur = prev + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;// [begin, keyi-1] keyi [keyi+1, end]point_QuickSort(a, begin, keyi - 1);point_QuickSort(a, keyi + 1, end);}
}
6.3 挖洞法
用一个形象生动的动画来说明一下此方法

再配一个简短的说明:
①先选出基准值,然后基准值的位置为坑位。Right先走,遇到比基准值小的数就停下。然后把这个小于基准值的数放到坑位,这个位置变成新的坑位。
②然后left走,遇到比基准值大的数停下,把这个大于基准值的数放到坑位,这个位置再变成新的坑位。
③以此类推,直到left和right相遇,然后将基准值放入最后的坑位即可。
int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin midi end 三个数选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else // a[begin] > a[midi]{if (a[midi] > a[end])return midi;else if (a[begin] < a[end])return begin;elsereturn end;}
}int dig(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int key = a[begin];int hole = begin;while (begin < end){// 右边找小,填到左边的坑while (begin < end && a[end] >= key){--end;}a[hole] = a[end];hole = end;// 左边找大,填到右边的坑while (begin < end && a[begin] <= key){++begin;}a[hole] = a[begin];hole = begin;}a[hole] = key;return hole;
}void dig_QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = dig(a, begin, end);dig_QuickSort(a, begin, keyi - 1);dig_QuickSort(a, keyi + 1, end);
}
7.归并排序
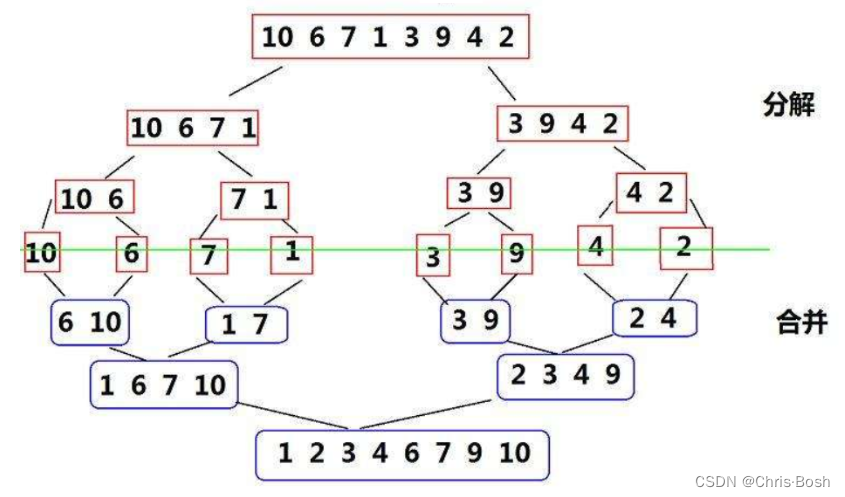
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。

简而言之就是先一个一个排,然后两个两个排,然后四个四个排,然后再全排序。
void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end)return;int mid = (begin + end) / 2;// [begin, mid][mid+1, end]_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);// [begin, mid][mid+1, end]归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, 0, n - 1, tmp);free(tmp);
}
8.排序性能比较
void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();hoare_QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("hoare_QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}
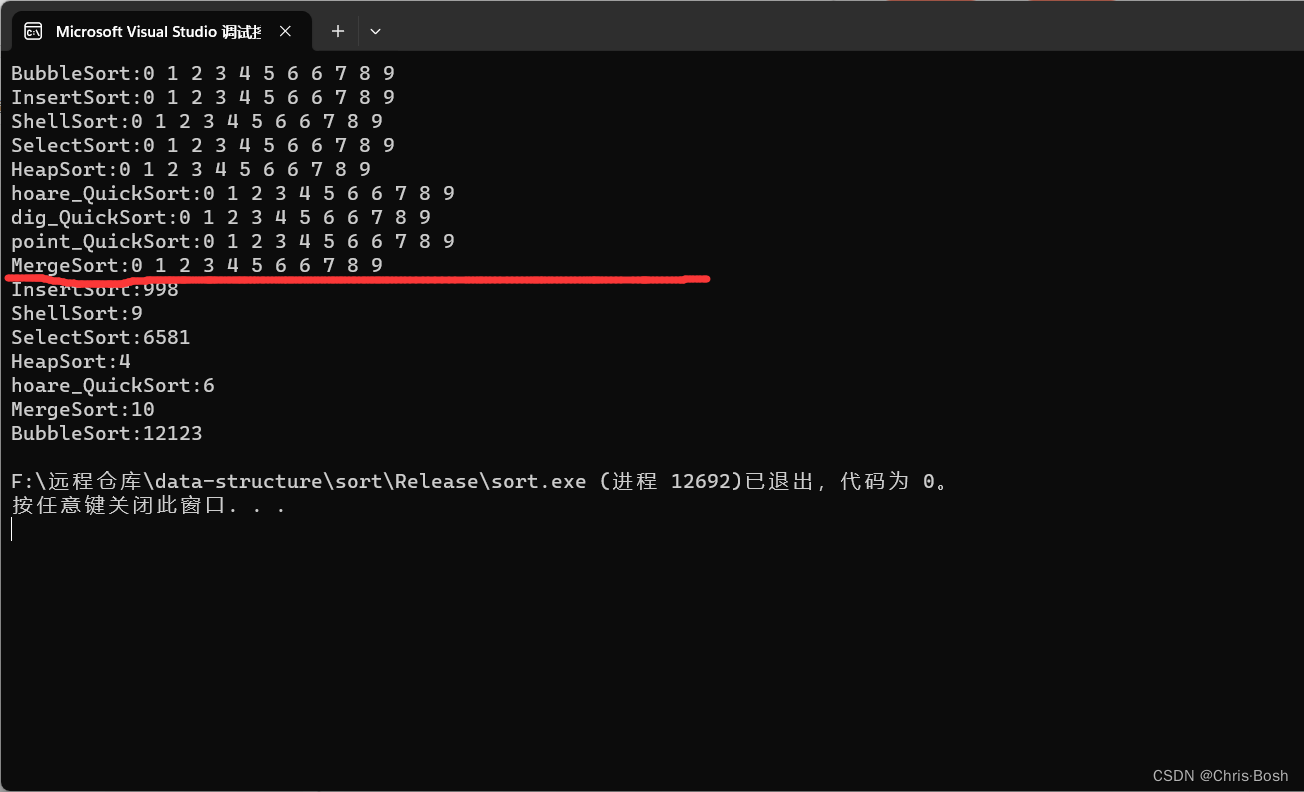
各种排序跑10W个数所需要的时间如上。
快速排序的三种算法,时间都差不多。只不过思想不一样罢了。
相关文章:

C语言数据结构-----常用七种排序介绍、分类、实现及性能比较
前言 ①排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 ②稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序&#…...

2023年山东省职业院校技能大赛高职组 “软件测试”赛项竞赛任务四 单元测试
任务四 单元测试 任务要求 题目1:任意输入2个正整数值分别存入x、y中,据此完成下述分析:若x≤0或y≤0,则提示:“输入不符合要求。”;若2值相同,则提示“可以构建圆形或正方形”;若2…...
在Redis客户端设置连接密码 并演示密码登录
我们先连接到Redis服务 然后 我们要输入 CONFIG SET requirepass “新密码” 例如 CONFIG SET requirepass "A15167"这样 密码就被设置成立 A15167 我们 输入 AUTH 密码 例如 AUTH A15167这里 返回OK说明成功了 然后 我们退出在登录就真的需要 redis-cli -h IP地…...

阿里云公有云平台
1. 请简要介绍一下公有云平台的基本概念和特点。 公有云是一种云计算模型,其中服务器、网络和存储资源等IT基础架构以虚拟资源的形式提供,并且可以通过互联网进行访问。这些资源是由第三方提供商共享并提供给用户的,包括计算、存储、网络等。…...
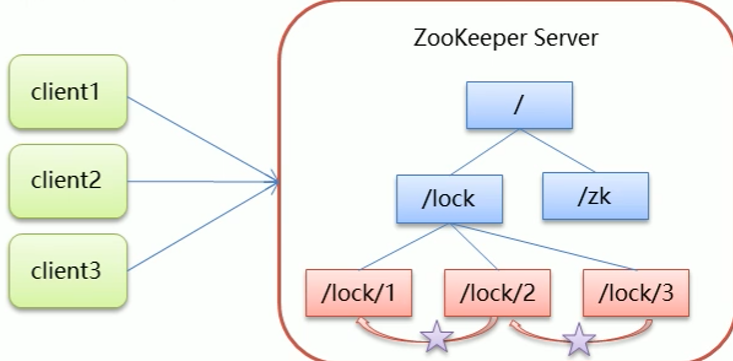
Zookeeper的学习笔记
Zookeeper概念 Zookeeper是一个树形目录服务,简称zk。 Zookeeper是一个分布式的、开源的分布式应用程序的协调服务 Zookeeper提供主要的功能包括:配置管理,分布式锁,集群管理 Zookeeper命令操作 zk数据模型 zk中的每一个节点…...

leetcode2两数加和问题(链表)
题目思路: ①创建一个int类型的局部变量,用来存储两个结点的Val值。 ②判断该Val值与10求余(mod)后是否大于0,如果大于0, 则需要在下一个结点进位。 ③最关键的步骤:实现l1,l2结点数值相加后构建新的存储求和后的结点࿰…...

VSCode中配置prettier和ESLint
文章目录 了解ESLint和Prettier的作用prettier配置ESLint配置常见问答ESLint 和Prettier 有什么区别?为什么我应该同时使用ESLint 和Prettier?在使用ESLint 和Prettier 时,有可能出现它们之间的规则冲突吗?我已经在项目中使用了ES…...

如何将本地websocket发布至公网并实现远程访问服务端
文章目录 1. Java 服务端demo环境2. 在pom文件引入第三包封装的netty框架maven坐标3. 创建服务端,以接口模式调用,方便外部调用4. 启动服务,出现以下信息表示启动成功,暴露端口默认99995. 创建隧道映射内网端口6. 查看状态->在线隧道,复制所创建隧道的公网地址加端口号7. 以…...

分享 | 软件测试的基本流程是什么?软件测试流程详细介绍
软件测试 软件测试和软件开发一样,是一个比较复杂的工作过程,如果无章法可循,随意进行测试势必会造成测试工作的混乱。为了使测试工作标准化、规范化,并且快速、高效、高质量地完成测试工作,需要制订完整且具体的测试…...
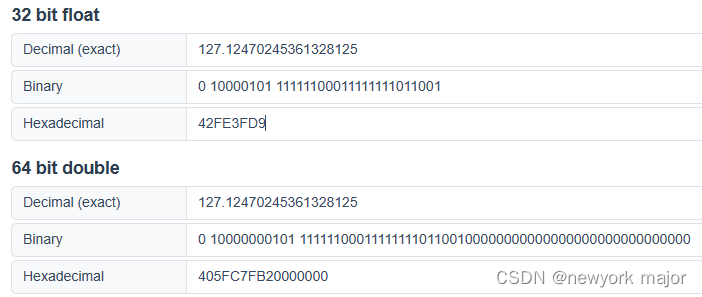
浮点数的转换--IEEE 754
IEEE754标准是一种浮点数表示标准,一般分为 单精度(32位的二进制数);双精度(64位的二进制数) 根据国际标准IEEE754,任意一个二进制浮点数V可以表示为下面形式: V (-1)^s *&#…...

若依框架介绍
RuoYi(若依)是一款基于Spring Boot、Spring Cloud等开源框架搭建的企业级开发平台,旨在提供全面的解决方案,简化企业级应用开发,提高开发效率。 主要特点: 1. 模块化设计 RuoYi采用模块化的设计࿰…...
iMazing2024免费版iOS移动设备管理软件
以自己的方式管理iPhone,让备受信赖的软件为您传输和保存音乐、消息、文件和数据。安全备份任何 iPhone、iPad 或 iPod touch。iMazing 功能强大、易于使用,称得上是 Mac 和 PC 上最好的 iOS 设备管理器。 正在为iTunes繁琐的操作发愁?设备数…...

Zookeeper整合Java实战,不同客户端使用汇总
Java学习面试指南:https://javaxiaobear.cn ZooKeeper应用的开发主要通过Java客户端API去连接和操作ZooKeeper集群。可供选择的Java客户端API有: ZooKeeper官方的Java客户端API。 第三方的Java客户端API,比如Curator。 ZooKeeper官方的客户…...

【python】Ubuntu下安装spyder及matplotlib中文显示
一、查看Ubuntu版本 $ lsb_release -a No LSB modules are available. Distributor ID: Ubuntu Description: Ubuntu 22.04.3 LTS Release: 22.04 Codename: jammy尝试用cat /etc/debian_version命令,竟然可以显示出来Debian的版本。 $ cat /etc/debian_version …...

《运维人员的未来:IT界的“万金油“如何继续闪耀光芒》
文章目录 每日一句正能量前言35岁被称为运维半衰期,究竟为何?如何顺利过渡半衰期运维的职业发展路径后记 每日一句正能量 凡事顺其自然,遇事处于泰然,得意之时淡然,失意之时坦然,艰辛曲折必然,历…...
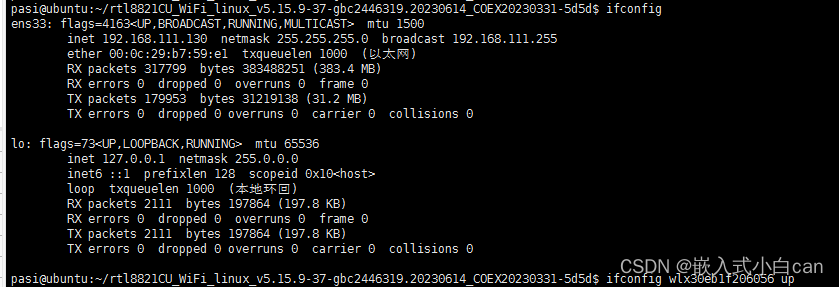
ip addr和ifconfig
ip addr可以显示更多信息,包括为启动的网络驱动如wlan,而ifocnfig只显示在线的驱动。若wlan是down的,则ip addr会显示信息,ifconfig不会显示信息。 ip addr: ifconfig:...

Crow:Middlewares 庖丁解牛7 after_handlers_call_helper
Crow:Middlewares 庖丁解牛6 middleware_call_helper-CSDN博客 介绍了对插件before_handle的调用 当完成了detail::middleware_call_helper的调用后,如果没有在before_handle中设置req被终止处理,也就是 if (!res.completed_) {need_to_call_after_handlers_ = true;handler…...

ts相关笔记(extends、infer、Pick、Omit)
最近刷了本ts小册,对一些知识点做下笔记。 extends extends 是一个关键字,用于对类型参数做一些约束。 A extends B 意味着 A 是 B 的子类型,比如下面是成立的 ‘abc’ extends string599 extends number 看下面例子: type …...
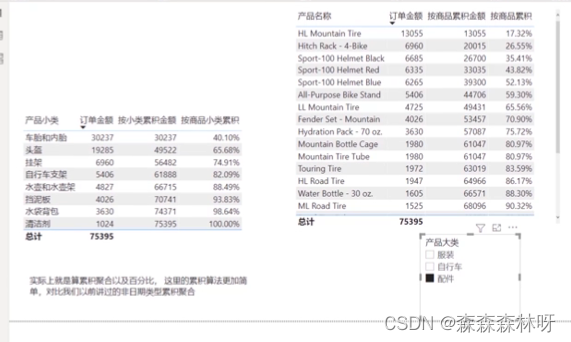
8.21 PowerBI系列之DAX函数专题-帕累托分析
需求 实现 1 按商品小类累积 var rollup_sales calculate(//计算当前累计销售额 [销售额], filter(allselected(order_2[产品小类]),sum(order_2[订单金额])<[销售额]) ) //按小类累积金额,filter内的销售额为选中的各小类的销售额 //金额从大到小累积,用&l…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...