智能优化算法应用:基于鱼鹰算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于鱼鹰算法3D无线传感器网络(WSN)覆盖优化 - 附代码
文章目录
- 智能优化算法应用:基于鱼鹰算法3D无线传感器网络(WSN)覆盖优化 - 附代码
- 1.无线传感网络节点模型
- 2.覆盖数学模型及分析
- 3.鱼鹰算法
- 4.实验参数设定
- 5.算法结果
- 6.参考文献
- 7.MATLAB代码
摘要:本文主要介绍如何用鱼鹰算法进行3D无线传感器网(WSN)覆盖优化。
1.无线传感网络节点模型
本文主要基于0/1模型,进行寻优。在二维平面上传感器节点的感知范围是一个以节点为圆心,半径为 R n R_n Rn的圆形区域,该圆形区域通常被称为该节点的“感知圆盘”, R n R_n Rn称为传感器节点的感知半径,感知半径与节点内置传感器件的物理特性有关,假设节点 n n n的位置坐标为 ( x n , y n , z n ) (x_n,y_n,z_n) (xn,yn,zn)在0-1感知模型中,对于平面上任意一点 p ( x p , y p , z p ) p(x_p,y_p,z_p) p(xp,yp,zp),则节点 n n n监测到区域内点 p p p的事件发生概率为:
P r ( n , p ) = { 1 , d ( n , p ) ≤ R n 0 , e s l e (1) P_r(n,p)=\begin{cases}1, \,d(n,p)\leq R_n\\ 0,\, esle \end{cases}\tag{1} Pr(n,p)={1,d(n,p)≤Rn0,esle(1)
其中 d ( n , p ) = ( x n − x p ) 2 + ( y n − y p ) 2 + ( z n − z p ) 2 d(n,p)=\sqrt{(x_n-x_p)^2+(y_n-y_p)^2 + (z_n-z_p)^2} d(n,p)=(xn−xp)2+(yn−yp)2+(zn−zp)2为点和之间的欧式距离。
2.覆盖数学模型及分析
现假定目标监测区域为二维平面,在区域 A r e a Area Area上投放同型结构传感器节点的数目为N,每个节点的位置坐标值假设已被初始化赋值,且节点的感知半径r。传感器节点集则表示为:
N o d e { x 1 , . . . , x N } (2) Node\{x_1,...,x_N\} \tag{2} Node{x1,...,xN}(2)
其中 n o d e i = { x i , y i , z i , r } node_i=\{x_i,y_i,z_i,r\} nodei={xi,yi,zi,r},表示以节点 ( x i , y i , z i ) (x_i,y_i,z_i) (xi,yi,zi)为圆心,r为监测半径的球,假定监测区域 A r e a Area Area被数字化离散为 m ∗ n ∗ l m*n*l m∗n∗l个空间点,空间点的坐标为 ( x , y , z ) (x,y,z) (x,y,z),目标点与传感器节点间的距离为:
d ( n o d e i , p ) = ( x i − x ) 2 + ( y i − y ) 2 + ( z i − z ) 2 (3) d(node_i,p)=\sqrt{(x_i-x)^2+(y_i-y)^2 + (z_i-z)^2}\tag{3} d(nodei,p)=(xi−x)2+(yi−y)2+(zi−z)2(3)
目标区域内点被传感器节点所覆盖的事件定义为 c i c_i ci。则该事件发生的概率 P c i P{c_i} Pci即为点 ( x , y , z ) (x,y,z) (x,y,z)被传感器节点 n o d e i node_i nodei所覆盖的概率:
P c o v ( x , y , z , n o d e i ) = { 1 , i f d ( n o d e i , p ) ≤ r 0 , e s l e (4) P_{cov}(x,y,z,node_i)=\begin{cases}1, if\,d(node_i,p)\leq r\\ 0,\, esle \end{cases}\tag{4} Pcov(x,y,z,nodei)={1,ifd(nodei,p)≤r0,esle(4)
我们将所有的传感器节点在目标监测环境中的区域覆盖率 C o v e r R a t i o CoverRatio CoverRatio定义为传感器节点集的覆盖面积与监测区域的面积之比,如公式所示:
C o v e r R a t i o = ∑ P c o v m ∗ n ∗ l (5) CoverRatio = \frac{\sum P_{cov}}{m*n*l}\tag{5} CoverRatio=m∗n∗l∑Pcov(5)
那我们的最终目标就是找到一组节点使得覆盖率最大。
3.鱼鹰算法
鱼鹰算法原理请参考:https://blog.csdn.net/u011835903/article/details/130542706
鱼鹰算法是寻找最小值。于是适应度函数定义为未覆盖率最小,即覆盖率最大。如下:
f u n = a r g m i n ( 1 − C o v e r R a t i o ) = a r g m i n ( 1 − ∑ P c o v m ∗ n ∗ l ) (6) fun = argmin(1 - CoverRatio) = argmin(1-\frac{\sum P_{cov}}{m*n*l}) \tag{6} fun=argmin(1−CoverRatio)=argmin(1−m∗n∗l∑Pcov)(6)
4.实验参数设定
无线传感器覆盖参数设定如下:
%% 设定WNS覆盖参数,
%% 默认输入参数都是整数,如果想定义小数,请自行乘以系数变为整数再做转换。
%% 比如范围1*1,R=0.03可以转换为100*100,R=3;
%区域范围为AreaX*AreaY*AreaZ
AreaX = 100;
AreaY = 100;
AreaZ = 100;
N = 20 ;%覆盖节点数
R = 15;%通信半径鱼鹰算法参数如下:
%% 设定鱼鹰优化参数
pop=30; % 种群数量
Max_iteration=30; %设定最大迭代次数
lb = ones(1,3*N);
ub = [AreaX.*ones(1,N),AreaY.*ones(1,N),AreaZ.*ones(1,N)];
dim = 3*N;%维度为3N,N个坐标点
5.算法结果


从结果来看,覆盖率在优化过程中不断上升。表明鱼鹰算法对覆盖优化起到了优化的作用。
6.参考文献
[1] 史朝亚. 基于PSO算法无线传感器网络覆盖优化的研究[D]. 南京理工大学.
7.MATLAB代码
相关文章:

智能优化算法应用:基于鱼鹰算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于鱼鹰算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于鱼鹰算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.鱼鹰算法4.实验参数设定5.算法结果6.参考文献7.MA…...
 骨架屏)
探索 Vue3 (五) 骨架屏
骨架屏是页面的一个空白版本,通常会在页面完全渲染之前,通过一些灰色的区块大致勾勒出轮廓,待数据加载完成后,再替换成真实的内容。 目前主流 UI库 都有骨架屏,如 Element-UI、Antd 可以看到使用起来非常简单&#x…...

java取出list中的某几个属性组成一个新的集合的几种方式
我用了三种方式,1:forEach循环;2:for循环;3:stream方法 package org.springblade.test;import java.util.ArrayList; import java.util.HashMap; import java.util.List; import java.util.Map; import java.util.stream.Collectors;public class Test {org.junit.jupiter.api…...
开源自托管导航页配置服务Dashy本地搭建结合内网穿透远程访问
开源自托管导航页配置服务Dashy本地搭建结合内网穿透远程访问 简介1. 安装Dashy2. 安装cpolar3.配置公网访问地址4. 固定域名访问 简介 Dashy 是一个开源的自托管的导航页配置服务,具有易于使用的可视化编辑器、状态检查、小工具和主题等功能。你可以将自己常用的一…...

Cloudstack多个管理服务器节点
https://docs.cloudstack.apache.org/en/4.18.0.0/adminguide/reliability.html 参考翻译: 代理上支持多个管理服务器 在具有多个管理服务器的Cloudstack环境中,可以根据算法配置代理,将其连接到哪个管理服务器。这对于内部负载均衡器或高可…...

31. Ajax
简介 AJAX 是 Asynchronous JavaScript And XML 的简称。直译为,异步的JS和XML。AJAX的实际意义是,不发生页面跳转、异步载入内容并改写页面内容的技术。AJAX也可以简单的理解为通过JS向服务器发送请求。 AJAX这门技术很早就被发明,但是直到…...
)
ArrayList源码学习笔记(3)
时隔两年,重新读ArrayList源码,轻松了很多,以问题的方式记录一下收获 装饰器模式 注释中提到ArrayList本身不是线程安全的,注释如下: * <p><strong>Note that this implementation is not synchronized.&…...

flutter怎么对ReorderableListView中的用于排序的控制手柄进行显示或隐藏
我在使用ReorderableListView创建可排序列表的时候,需要在编辑的时候才显示右侧的控制排序的手柄。研究了半天,配合搜索引擎,才找到正确的方案。 答案很简单,就是在它的属性当中有一个叫做:buildDefaultDragHandles的…...

python 1200例——【9】斐波那契数列
文章目录 定义求解方法1. 递归方法2. 循环方法3. 动态规划方法4. 矩阵方法总结:定义 斐波那契数列(Fibonacci sequence)是一个在自然世界中经常出现的数学序列。它是由0和1开始,然后的每个数字都是前两个数字的和。因此,斐波那契数列的前几个数字是:0, 1, 1, 2, 3, 5, 8…...
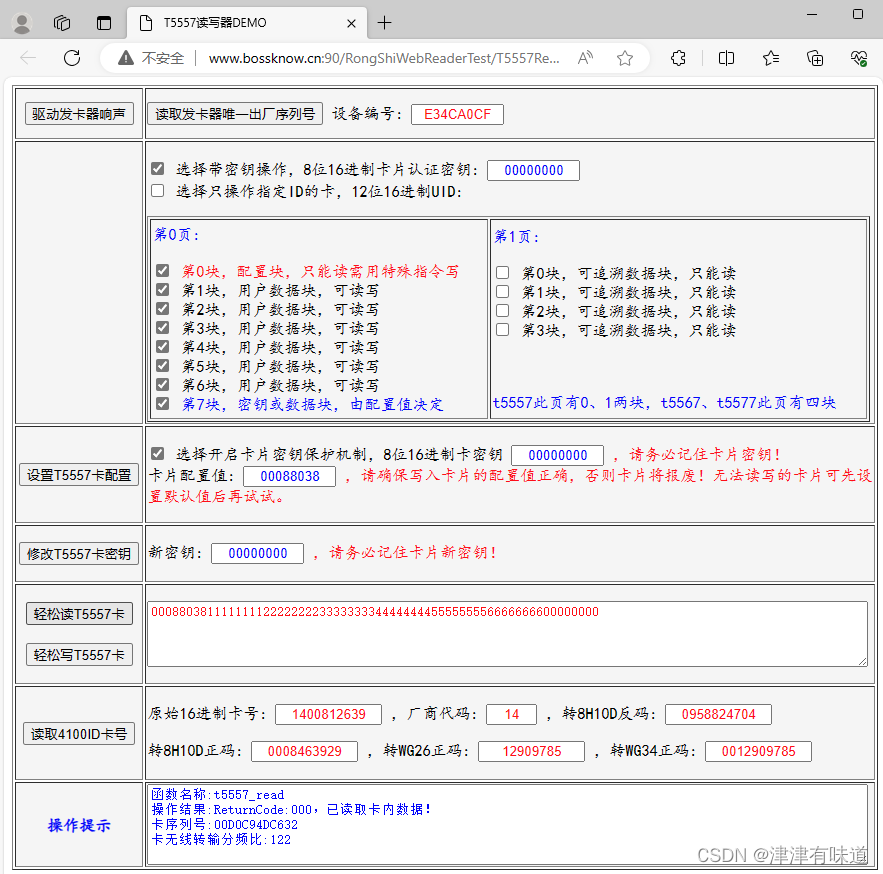
JavaScript读写T5557卡源码
本示例使用发卡器: https://item.taobao.com/item.htm?spma1z10.5-c-s.w4002-21818769070.13.48ce6f89XlQ9Vf&id675212889085 <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-t…...
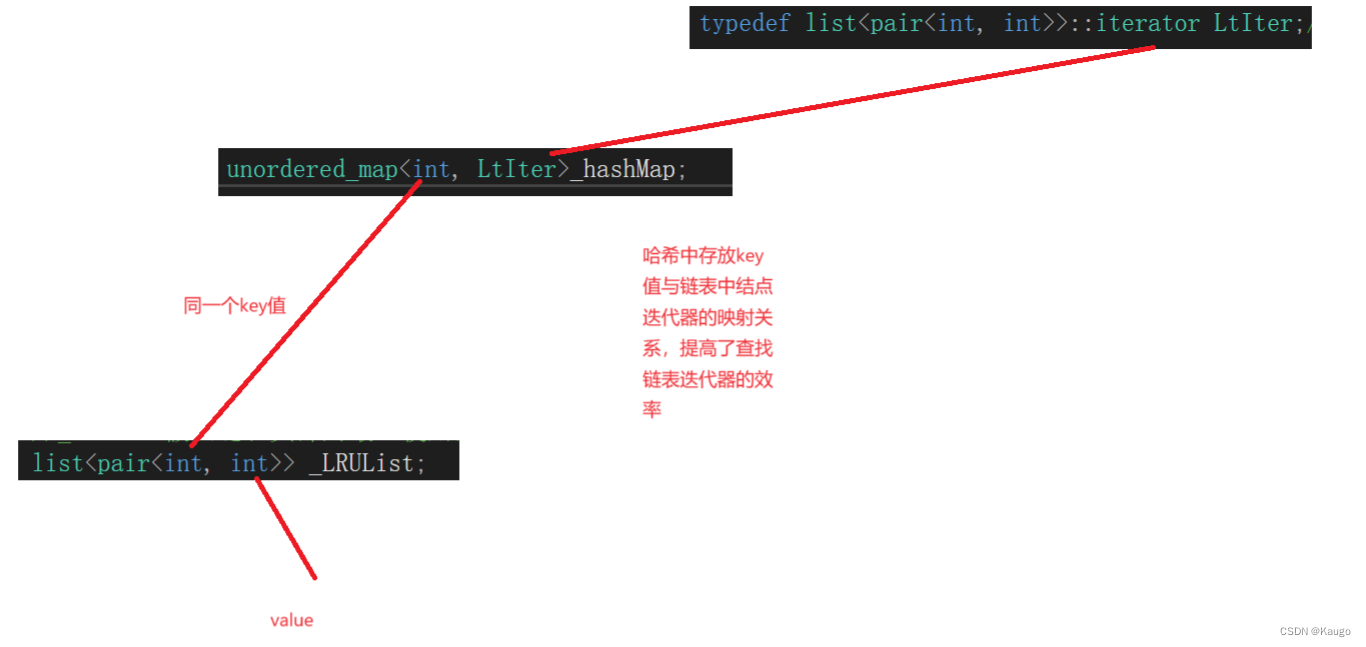
【数据结构】LRU缓存的简单模拟实现(leetcode力扣146LRU缓存)
文章目录 一、定义二、LRU模拟实现二、代码实现 一、定义 LRU是Least Recently Used的缩写,意思是最近最少使用,它是一种Cache替换算法。 Cache的容量有限,因此当Cache的容量用完后,而又有新的内容需要添加进来时, 就…...
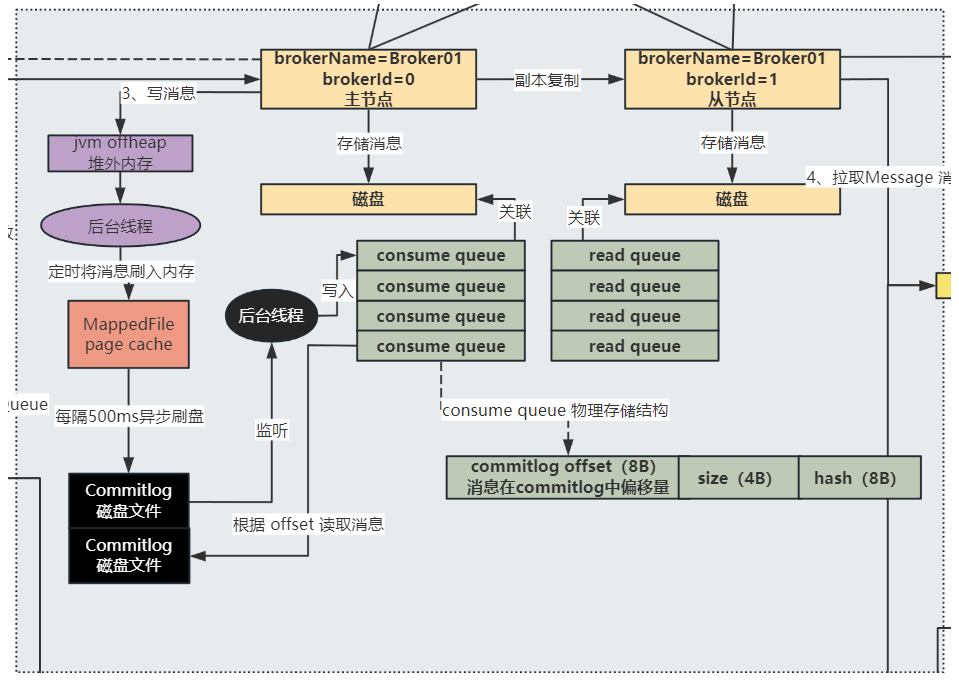
基于电商场景的高并发RocketMQ实战-Commitlog基于内存的高并发写入优化、基于JVM offheap的内存读写分离机制
🌈🌈🌈🌈🌈🌈🌈🌈 【11来了】文章导读地址:点击查看文章导读! 🍁🍁🍁🍁🍁🍁dz…...
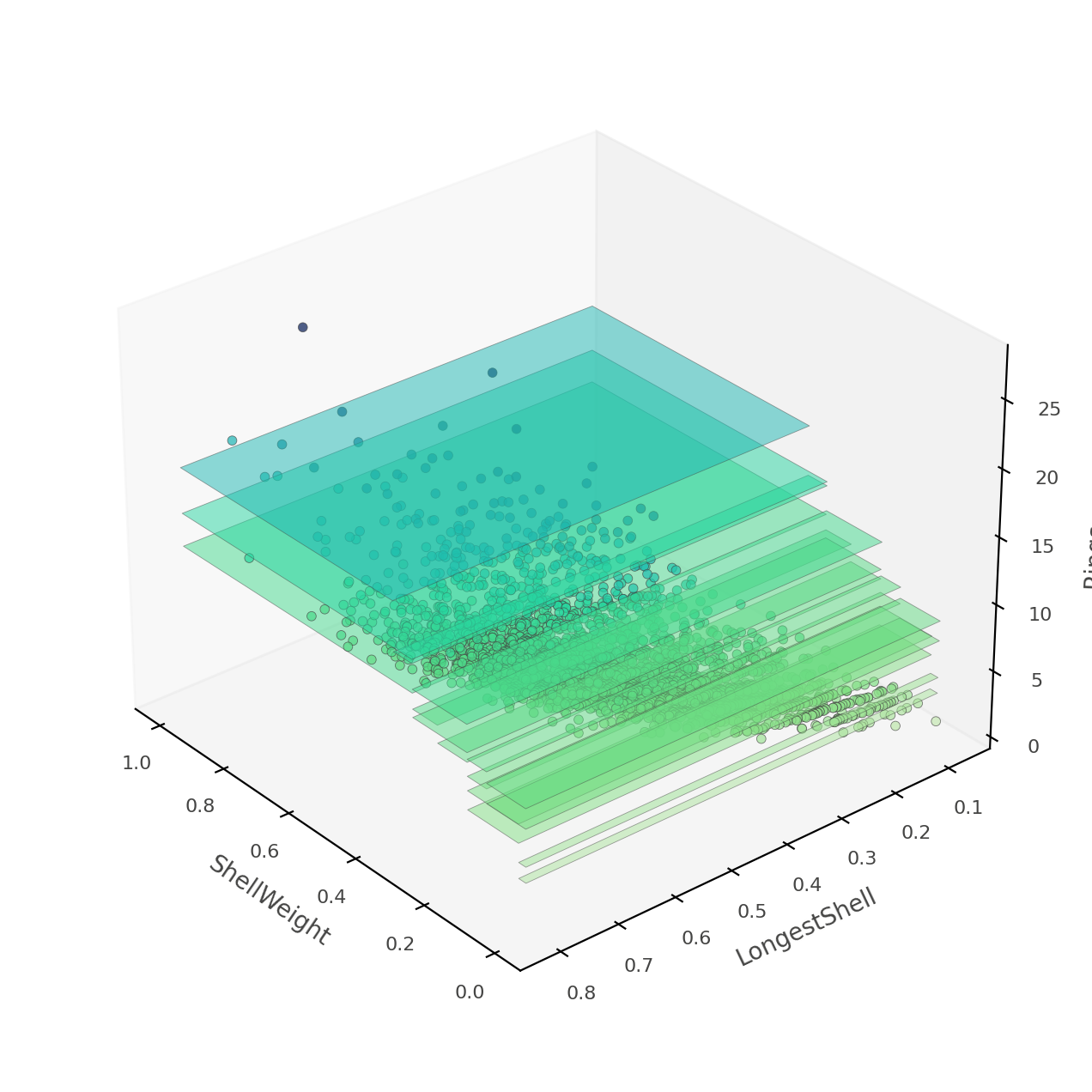
工具系列:TensorFlow决策森林_(3)使用dtreeviz可视化
文章目录 介绍设置安装 TF-DF 和 dtreeviz导入库 可视化分类树加载、清洗和准备数据分割训练/测试集并训练模型训练一个随机森林分类器显示决策树检查叶节点统计信息决策树如何对实例进行分类特征空间划分 可视化回归树加载、清洗和准备数据分割训练/测试集并训练模型训练一个随…...
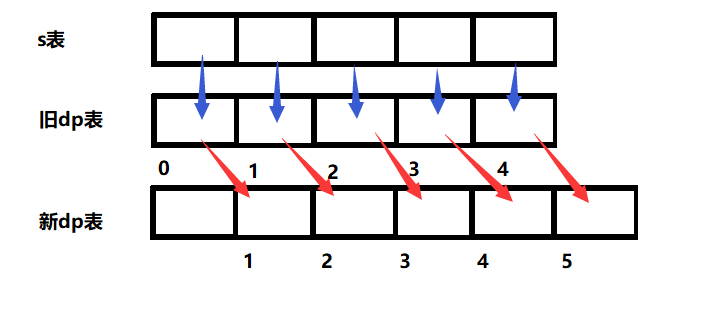
【算法学习】斐波那契数列模型-动态规划
前言 我在算法学习过程中,针对斐波那契数列模型的动态规划的例题进行了一个整理,并且根据标准且可靠一点的动态规划解题思路进行求解类似的动归问题,来达到学习和今后复习的必要。 所谓的斐波那契数列模型,即当前状态的值等于前两…...
ES的安装和RestClient的操作
目录 初识elasticsearch 什么是elasticsearch elasticsearch的发展 Lucene的优缺点 elasticsearch的优势 倒排索引 es与mysql的概念对比 文档 索引 概念对比 架构 安装es 安装kibana 安装ik分词器 分词器 安装ik分词器 ik分词器的拓展和停用词典 操作索引库…...
)
访问者模式(Visitor)
访问者模式(Visitor Pattern)是一种将算法与对象结构分离的行为型设计模式。这种模式主要用于对一个由许多不同类型的对象构成的复杂对象结构(如组合结构)进行操作,而不需要对这些对象的类进行修改。 访问者模式涉及以下几个角色: 访问者(Visitor):为每一个具体元素类…...

ATTCK红队评估一
一、环境搭建 主机 ip地址 win7外网服务器(两张网卡) 外网:192.168.92.135 内网:192.168.52.143 server2003域成员主机 内网:192.168.52.141 server2008域空主机 内网:192.168.52.138 kali攻击机 …...
W5500-EVB-Pico评估版介绍
文章目录 1 概述2 板载资源2.1 硬件规格2.2 硬件规格2.3 工作条件 3 参考资料3.2 原理图3.3 尺寸图 (单位 : mm)3.4 参考例程 4 硬件协议栈优势 1 概述 W5500-EVB-Pico是基于树莓派RP2040和完全硬连线TCP/IP控制器W5500的微控制器开发板-基本上与树莓派Pico板相同,但…...
单聊和群聊
TCP协议单聊 服务端: import java.awt.BorderLayout; import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.io.PrintWriter; import java.net.ServerSocket; import java.net.Socket; import java.util.Vec…...

Swift 检测 iCloud状态
Show me the code: func isICloudContainerAvailable() -> Bool {if let _ FileManager.default.ubiquityIdentityToken {return true} else {return false} }推荐一下刚上线的 App 熊猫小账本,里面有用到这篇博客讲的内容 熊猫小账本 一个简洁的记账 App&…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
