【数据结构和算法】找到最高海拔
其他系列文章导航
Java基础合集
数据结构与算法合集设计模式合集
多线程合集
分布式合集
ES合集
文章目录
其他系列文章导航
文章目录
前言
一、题目描述
二、题解
2.1 前缀和的解题模板
2.1.1 最长递增子序列长度
2.1.2 寻找数组中第 k 大的元素
2.1.3 最长公共子序列长度
2.1.4 寻找数组中第 k 小的元素
2.2 方法一:前缀和(差分数组)
三、代码
3.2 方法一:前缀和(差分数组)
四、复杂度分析
4.2 方法一:前缀和(差分数组)
前言
这是力扣的 1732 题,难度为简单,解题方案有很多种,本文讲解我认为最奇妙的一种。
这是一道非常经典的前缀和问题,虽然看似简单,但它却能让你深入理解前缀和的特点。
一、题目描述
有一个自行车手打算进行一场公路骑行,这条路线总共由 n + 1 个不同海拔的点组成。自行车手从海拔为 0 的点 0 开始骑行。
给你一个长度为 n 的整数数组 gain ,其中 gain[i] 是点 i 和点 i + 1 的 净海拔高度差(0 <= i < n)。请你返回 最高点的海拔 。
示例 1:
输入:gain = [-5,1,5,0,-7] 输出:1 解释:海拔高度依次为 [0,-5,-4,1,1,-6] 。最高海拔为 1 。
示例 2:
输入:gain = [-4,-3,-2,-1,4,3,2] 输出:0 解释:海拔高度依次为 [0,-4,-7,-9,-10,-6,-3,-1] 。最高海拔为 0 。
提示:
n == gain.length1 <= n <= 100-100 <= gain[i] <= 100
二、题解
2.1 前缀和的解题模板
前缀和算法是一种在处理数组或链表问题时常用的技巧,它可以有效地减少重复计算,提高算法的效率。下面是一些常见的使用前缀和算法的题目以及解题思路:
2.1.1 最长递增子序列长度
题目描述:给定一个无序数组,求最长递增子序列的长度。
解题思路:可以使用前缀和和单调栈来解决这个问题。首先,遍历数组,计算出前缀和。然后,使用单调栈记录当前递增子序列的起始位置。遍历数组时,如果当前元素大于前缀和,说明可以扩展当前递增子序列,将当前位置入栈。如果当前元素小于等于前缀和,说明当前递增子序列已经结束,弹出栈顶元素。最后,栈中剩余的元素即为最长递增子序列的起始位置,计算长度即可。
2.1.2 寻找数组中第 k 大的元素
题目描述:给定一个无序数组和一个整数k,找到数组中第k大的元素。
解题思路:可以使用前缀和和快速选择算法来解决这个问题。首先,计算出数组的前缀和。然后,使用快速选择算法在数组中找到第k小的元素。具体实现中,每次选择一个枢轴元素,将数组分成两部分,小于枢轴的元素和大于枢轴的元素。如果枢轴左边的元素个数小于k,则在左边的子数组中继续查找;如果枢轴左边的元素个数大于等于k,则在右边的子数组中继续查找。最后,当找到第k小的元素时,返回该元素即可。
2.1.3 最长公共子序列长度
题目描述:给定两个字符串,求最长公共子序列的长度。
解题思路:可以使用动态规划算法来解决这个问题。如果字符串长度分别为m和n,则可以定义一个二维数组dp[m+1][n+1],其中dp[i][j]表示字符串s1的前i个字符和字符串s2的前j个字符的最长公共子序列长度。根据动态规划的思想,状态转移方程为dp[i][j] = max(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])。如果s1[i-1]等于s2[j-1],则dp[i][j] = dp[i-1][j-1] + 1;否则dp[i][j]取其他两种情况中的较大值。最终结果为dp[m][n]。
2.1.4 寻找数组中第 k 小的元素
题目描述:给定一个无序数组和一个整数k,找到数组中第k小的元素。
解题思路:可以使用前缀和和快速选择算法来解决这个问题。具体实现与寻找第k大元素类似,只不过最后返回的是第k小的元素而非第k大的元素。
2.2 方法一:前缀和(差分数组)
解这个问题需要注意以下几点:
- 理解题意:首先,要明确题目的要求,理解自行车手的骑行路线和海拔变化的关系。根据题目描述,自行车手从海拔为0的点开始骑行,通过一系列的海拔变化,最终要找到最高点的海拔。
- 分析海拔变化:根据给定的gain数组,可以分析出自行车手的海拔变化。gain[i]表示点i和点i+1之间的净海拔高度差。通过累加这些高度差,可以计算出经过每个点后的总海拔变化。
- 确定最高点的海拔:在计算出总的海拔变化后,需要找到最高点的海拔。这可以通过比较累加海拔和初始海拔的大小来实现。最高点的海拔即为累加海拔和初始海拔中的较大值。
- 注意数组边界条件:在处理gain数组时,需要注意数组的边界条件。例如,gain[0]表示起点和终点之间的海拔高度差,而gain[n-1]表示倒数第二个点和终点之间的海拔高度差。
- 代码实现:最后,根据上述分析,可以使用Python等编程语言实现相应的算法。在实现过程中,需要注意代码的简洁性和可读性,同时也要注意处理可能的异常情况。
思路与算法:
我们假设每个点的海拔为 hi ,由于 gain[i] 表示第 i 个点和第 i+1 个点的海拔差,因此
gain[i] = h(i+1) − hi,那么:
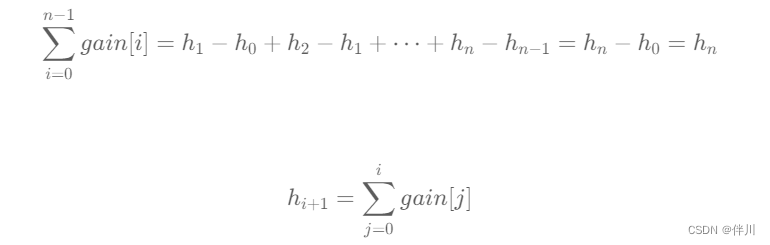
可以发现,每个点的海拔都可以通过前缀和的方式计算出来。因此,我们只需要遍历一遍数组,求出前缀和的最大值,即为最高点的海拔。
实际上题目中的 gain 数组是一个差分数组,对差分数组求前缀和即可得到原海拔数组。然后求出原海拔数组的最大值即可。
三、代码
3.2 方法一:前缀和(差分数组)
Java版本:
class Solution {public int largestAltitude(int[] gain) {int high = 0, max = 0;for (int h : gain) {high += h;max = Math.max(max, high);}return max;}
}C++版本:
class Solution {
public:int largestAltitude(std::vector<int>& gain) {int high = 0, max = 0;for (int h : gain) {high += h;max = std::max(max, high);}return max;}
};
Python版本:
class Solution:def largestAltitude(self, gain: List[int]) -> int:high = 0max_altitude = 0for h in gain:high += hmax_altitude = max(max_altitude, high)return max_altitude
Go版本:
func largestAltitude(gain []int) int {high, max := 0, 0for _, h := range gain {high += hif high > max {max = high}}return max
}func main() {gain := []int{-5, 1, 5, 0, -7}result := largestAltitude(gain)fmt.Println(result)
}
四、复杂度分析
4.2 方法一:前缀和(差分数组)
- 时间复杂度: O(n),其中 n 为数组 gain 的长度。
- 空间复杂度: O(1)。
相关文章:
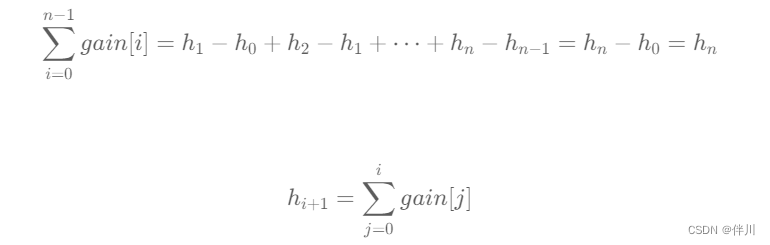
【数据结构和算法】找到最高海拔
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、题目描述 二、题解 2.1 前缀和的解题模板 2.1.1 最长递增子序列长度 2.1.2 寻找数组中第 k 大的元素 2.1.3 最长公共子序列…...

redis相关问题
1、概述: 1. 非关系型数据库 2. 是分布式缓存数据库 3. 使用 key -value结构存储 2、作用: 用作缓存降低数据库压力,提高性能;可以用作消息队列(削峰、解耦、异步调用) 3、基础语法: 基础命令…...

第41节: Vue3 watch函数
在UniApp中使用Vue3框架时,你可以使用watch函数来观察和响应Vue实例上的数据变化。以下是一个示例,演示了如何在UniApp中使用Vue3框架使用watch函数: <template> <view> <input v-model"message" type"text…...

Centos7:升级gcc、g++到版本5.2.0
背景 Centos7.9版本默认的g版本是4.8.5,在实践golang项目中,用到C14,编译时会报错:gcc: error: unrecognized command line option ‘-stdc14’ 因此,gcc需要升级到更高版本,我这里使用源码编译形式升级到g…...

Pytohn data mode plt
文章目录 文件的读写创建.csv类型的文件,并读取文件创建.xlsx文件 使用Python做图生成数据集切片取值操作修改张量中指定位置的数据 知识点torch.arange(x)torch.tensor(2)Atorch.randn(36).reshape(6,6)shapenumel()reshape(x,y,z)torch.zeros(3,3,4)torch.ones(2,…...

内网离线搭建之----kafka集群
1.系统版本 虚拟机192.168.9.184 虚拟机192.168.9.185 虚拟机192.168.9.186系统 centos7 7.6.1810 2.依赖下载 ps:置顶资源里已经下载好了,直接用!!!!!!!!…...
)
5.1 显示窗口的内容(一)
一,如何显示窗口的内容? 显示器用于在物理硬件(如计算机显示器或触摸屏显示器)上显示窗口的内容。 屏幕API提供的功能允许我们创建同时写入多个窗口和显示的应用程序。屏幕支持多个显示器,但创建和管理使用多个显示器…...
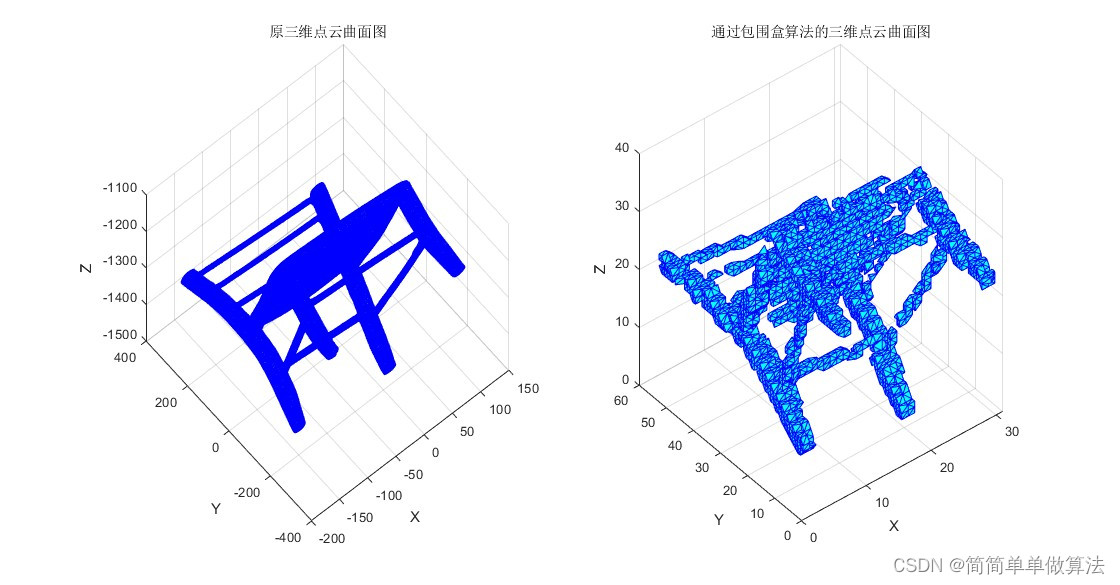
基于包围盒算法的三维点云数据压缩和曲面重建matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1 包围盒构建 4.2 点云压缩 4.3 曲面重建 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 ...........................................…...
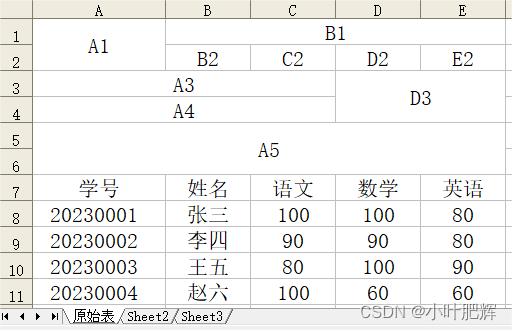
关于Python里xlwings库对Excel表格的操作(十八)
这篇小笔记主要记录如何【设置单元格数据的对齐方式】。前面的小笔记已整理成目录,可点链接去目录寻找所需更方便。 【目录部分内容如下】【点击此处可进入目录】 (1)如何安装导入xlwings库; (2)如何在Wps下…...
VScode远程连接服务器,Pycharm专业版下载及远程连接(深度学习远程篇)
Visual Code、PyCharm专业版,本地和远程交互。 远程连接需要用到SSH协议的技术,常用的代码编辑器vscode 和 pycharm都有此类功能。社区版的pycharm是免费的,但是社区版不支持ssh连接服务器,只有专业版才可以,需要破解…...
------$bus)
Vue2和Vue3组件间通信方式汇总(3)------$bus
组件间通信方式是前端必不可少的知识点,前端开发经常会遇到组件间通信的情况,而且也是前端开发面试常问的知识点之一。接下来开始组件间通信方式第三弹------$bus,并讲讲分别在Vue2、Vue3中的表现。 Vue2Vue3组件间通信方式汇总(1)…...
PyTorch加载数据以及Tensorboard的使用
一、PyTorch加载数据初认识 Dataset:提供一种方式去获取数据及其label 如何获取每一个数据及其label 总共有多少的数据 Dataloader:为后面的网络提供不同的数据形式 数据集 在编译器中导入Dataset from torch.utils.data import Dataset 可以在jupyter中查看Dataset官方文档&…...

TensorFlow是什么
TensorFlow是什么 Tensorflow是一个Google开发的第二代机器学习系统,克服了第一代系统DistBelief仅能开发神经网络算法、难以配置、依赖Google内部硬件等局限性,应用更加广泛,并且提高了灵活性和可移植性,速度和扩展性也有了大幅…...
docker-compose 安装Sonar并集成gitlab
文章目录 1. 前置条件2. 编写docker-compose-sonar.yml文件3. 集成 gitlab4. Sonar Login with GitLab 1. 前置条件 安装docker-compose 安装docker 创建容器运行的特有网络 创建挂载目录 2. 编写docker-compose-sonar.yml文件 version: "3" services:sonar-postgre…...

支付平台在选择服务器租用时要注意什么?
如果要建设一个支付平台的话要进行服务器租用,一旦涉及到钱的方面就必须要顾虑到多方面,这样才能保证安全性,今天小编就给大家讲一讲要注意什么呢? 1、带宽:带宽是业务稳定性的直接因素,只有带宽充足,这样…...

IDEA2018升级2023,lombok插件不兼容导致get/set方法无法使用
1、问题 最近了解到一款叫CodeGeeX 的智能编程助手,想要试用一下,但是IDEA2018版本太低了,没有CodeGeeX插件,于是打算将IDEA升级到2023.2.5版本,具体升级过程略过,升级完成后,启动项目…...

企业微信服务商代开发模式获取授权企业的客户信息
服务商代开发素材: 服务商可信ip 企业微信认证 测试时不用再次创建一个企业微信,可以用当前的企业微信作为授权企业使用一、创建代开发应用模板 1,代开发模板回调URL配置 参考 注意:保存代开发应用模板时的corpId是服务商的企业…...

库存管理方法有哪些
库存管理是工作中一个离不开的话题,不管是仓管还是业务员都或多或少接触过库存管理方面的工作,例如:进货、销售、库存盘点等等这些都属于库存管理的范筹,那么库存管理方法有哪些?用哪种方法管理库存比较好,…...

数字化车间推动制造业生产创新
一、数字化车间应用场景 1:资源智能化管理 数字化车间通过搭建智能化的设备监测系统,实时采集和监控设备的运行状态和生产数据,对设备进行实时管理和维护,降低故障率和维修成本。同时,通过对生产过程中的数据采集和分…...
Linux的安装及管理程序
一、如何在linux安装卸载软件 1. 编译安装 灵活性较高 难度较大 可以安装较新的版本 2. rpm安装(redhat) linux 包安装 查软件信息:是否安装,文件列表 rpm 软件名 3. yum yum是RPM升级版本,解决rpm的弊端 安装软件 首…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...

前端工具库lodash与lodash-es区别详解
lodash 和 lodash-es 是同一工具库的两个不同版本,核心功能完全一致,主要区别在于模块化格式和优化方式,适合不同的开发环境。以下是详细对比: 1. 模块化格式 lodash 使用 CommonJS 模块格式(require/module.exports&a…...
