leetcode——打家劫舍问题汇总
本章汇总一下leetcode中的打家劫舍问题,使用经典动态规划算法求解。
1、梦开始的地方——打家劫舍(★)

本题关键点就是不能在相邻房屋偷东西。
采用常规动态规划做法:
- 根据题意设定dp数组,dp[i]的含义为:前i个房屋内,能偷的最高金额。
- 需要初始化dp[0]=0,dp[1]=nums[0]。
- 遍历dp数组,对应两种情况:偷或者不偷。 递推公式为:
-
dp[i] = Math.max(dp[i-1] , dp[i-2]+nums[i-1]);
-
-
最后返回dp数组最后一个数。
java代码如下:
class Solution {public int rob(int[] nums) {if(nums.length == 1) return nums[0];int[] dp = new int[nums.length+1]; //dp[i]:前i个房屋内,能偷的最高金额。dp[1] = nums[0];for(int i=2; i<=nums.length; i++){dp[i] = Math.max(dp[i-1] , dp[i-2]+nums[i-1]); //分别对应偷或者不偷}return dp[nums.length];}
}2、打家劫舍II

本题是上一题的进阶版,区别在于收尾两个房屋也是相邻的,不能同时偷。 此时无非就两种情况:
- 不偷首房屋。
- 不偷尾房屋。
分别设两个dp数组对应以上两种情况即可,思路还是类似上一题。
java代码如下:
class Solution {public int rob(int[] nums) {if(nums.length == 1) return nums[0];int[] dp1 = new int[nums.length]; //不偷首房屋int[] dp2 = new int[nums.length]; //不偷尾房屋dp1[1] = nums[1];dp2[1] = nums[0];for(int i=2; i<nums.length; i++){dp1[i] = Math.max(dp1[i-1] , dp1[i-2]+nums[i]);dp2[i] = Math.max(dp2[i-1] , dp2[i-2]+nums[i-1]);}return dp1[nums.length-1] > dp2[nums.length-1] ? dp1[nums.length-1] : dp2[nums.length-1];}
}3、打家劫舍III(★)
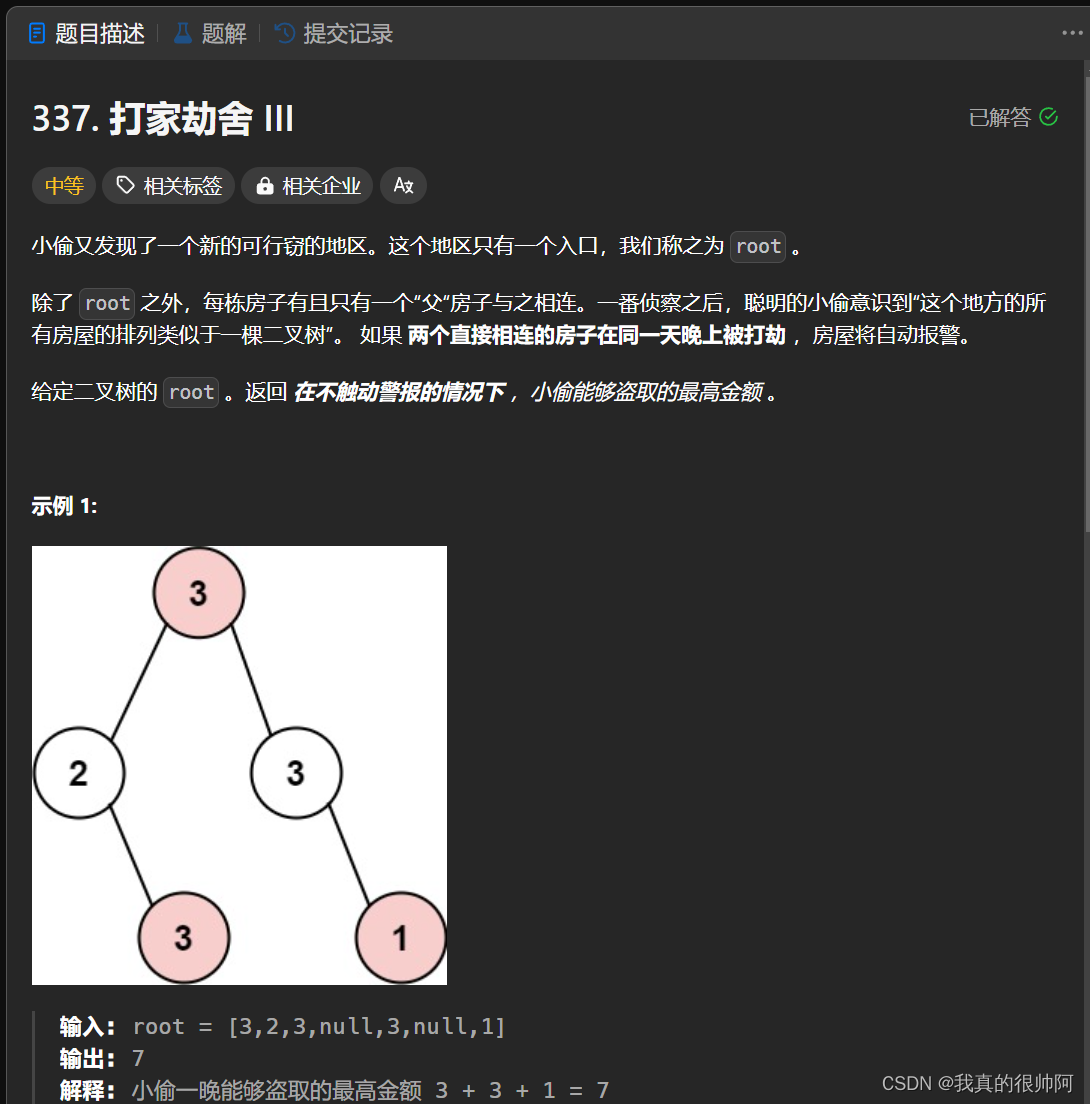
本题是从数组型dp转化为树形dp,由于父节点的状态需要从孩子节点的状态推出来,因此需要使用后序遍历。
首先需要定义一个递归函数dfs,参数为当前节点,返回值为长度为2的数组,即dp数组,dp[0]代表选当场节点,dp[1]代表不选当前节点。 如下:
int[] dfs(TreeNode node)
接下来确定终止条件:
if(node == null) return new int[] {0,0};
使用后序遍历递归遍历左右子树:
//递归左右子树
int[] left = dfs(node.left);
int[] right = dfs(node.right);
确定单层递归逻辑:
//分别对应偷与不偷的情况:
int rob = node.val + left[1] + right[1];
int no_rob = Math.max(left[0],left[1]) + Math.max(right[0],right[1]);
java代码如下:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int rob(TreeNode root) {int[] ans = dfs(root);return Math.max(ans[0],ans[1]);}private int[] dfs(TreeNode node){if(node == null) return new int[] {0,0};//递归左右子树int[] left = dfs(node.left);int[] right = dfs(node.right);int rob = node.val + left[1] + right[1];int no_rob = Math.max(left[0],left[1]) + Math.max(right[0],right[1]);return new int[] {rob,no_rob};}
}
相关文章:

leetcode——打家劫舍问题汇总
本章汇总一下leetcode中的打家劫舍问题,使用经典动态规划算法求解。 1、梦开始的地方——打家劫舍(★) 本题关键点就是不能在相邻房屋偷东西。 采用常规动态规划做法: 根据题意设定dp数组,dp[i]的含义为:…...
Java经典框架之Spring MVC
Spring MVC Java 是第一大编程语言和开发平台。它有助于企业降低成本、缩短开发周期、推动创新以及改善应用服务。如今全球有数百万开发人员运行着超过 51 亿个 Java 虚拟机,Java 仍是企业和开发人员的首选开发平台。 课程内容的介绍 1. Spring MVC 入门案例 2. 基…...

Golang make vs new
文章目录 1.简介2.区别3.new 可以初始化 slice,map 和 channel 吗?4.make 可以初始化其他类型吗?5.小结参考文献 1.简介 在 Go 语言中,make 和 new 是两个用于创建对象的内建函数,但它们有着不同的用途和适用范围。 …...

Arthas
概述 Arthas(阿尔萨斯) 能为你做什么? Arthas 是Alibaba开源的Java诊断工具,深受开发者喜爱。 当你遇到以下类似问题而束手无策时,Arthas可以帮助你解决: 这个类从哪个 jar 包加载的?为什么会…...

IP代理科普| 共享IP还是独享IP?两者的区别与优势
通俗地讲,共享IP就像乘坐公共汽车一样,您可以到达目的地,但将与其他乘客共享旅程,座位很可能是没有的。独享IP就像坐出租车一样,您可以更快到达目的地,由于车上只有您一个人,座位是您一个人专用…...
龙芯loongarch64服务器编译安装tensorflow-io-gcs-filesystem
前言 安装TensorFlow的时候,会出现有些包找不到的情况,直接使用pip命令也无法安装,比如tensorflow-io-gcs-filesystem,安装的时候就会报错: 这个包需要自行编译,官方介绍有限,这里我讲解下 编译 准备 拉取源码:https://github.com/tensorflow/io.git 文章中…...

开源持续测试平台Linux MeterSphere本地部署与远程访问
文章目录 前言1. 安装MeterSphere2. 本地访问MeterSphere3. 安装 cpolar内网穿透软件4. 配置MeterSphere公网访问地址5. 公网远程访问MeterSphere6. 固定MeterSphere公网地址 前言 MeterSphere 是一站式开源持续测试平台, 涵盖测试跟踪、接口测试、UI 测试和性能测试等功能&am…...

Kubernetes(K8S)快速入门
概述 在本门课程中,我们将会学习K8S一些非常重要和核心概念,已经操作这些核心概念对应组件的相关命令和方式。比如Deploy部署,Pod容器,调度器,Service服务,Node集群节点,Helm包管理器等等。 在…...
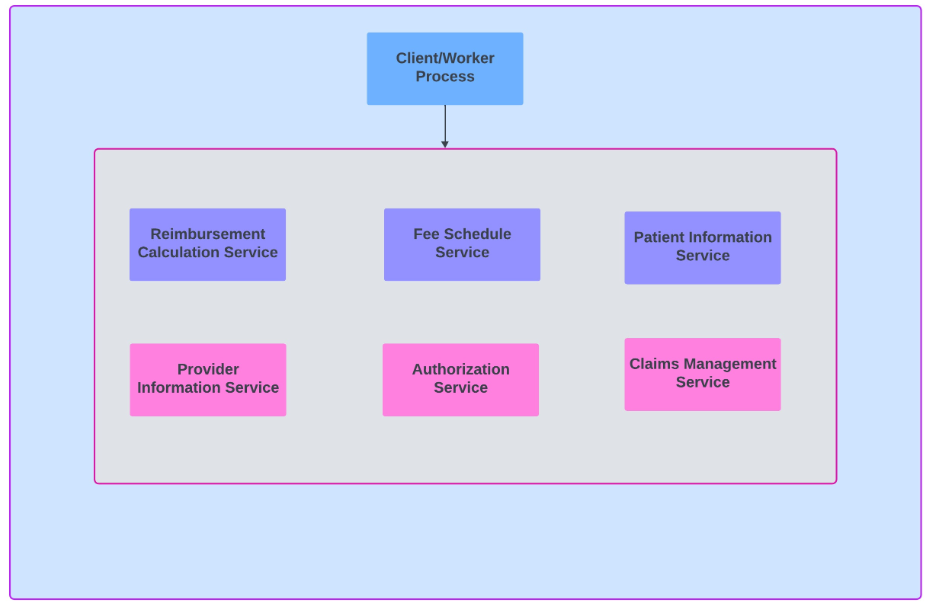
将遗留系统分解为微服务:第 2 部分
在当今不断发展的技术环境中,从整体架构向微服务的转变对于许多企业来说都是一项战略举措。这在报销计算系统领域尤其重要。正如我在上一篇文章第 1 部分应用 Strangler 模式将遗留系统分解为微服务-CSDN博客中提到的,让我们探讨如何有效管理这种转变。 …...

RK3588平台开发系列讲解(AI 篇)RKNN-Toolkit2 模型的加载转换
文章目录 一、Caffe 模型加载接口二、TensorFlow 模型加载接口三、TensorFlowLite 模型加载接口四、ONNX 模型加载五、DarkNet 模型加载接口六、PyTorch 模型加载接口沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 RKNN-Toolkit2 目前支持 Caffe、TensorFlow、Tensor…...
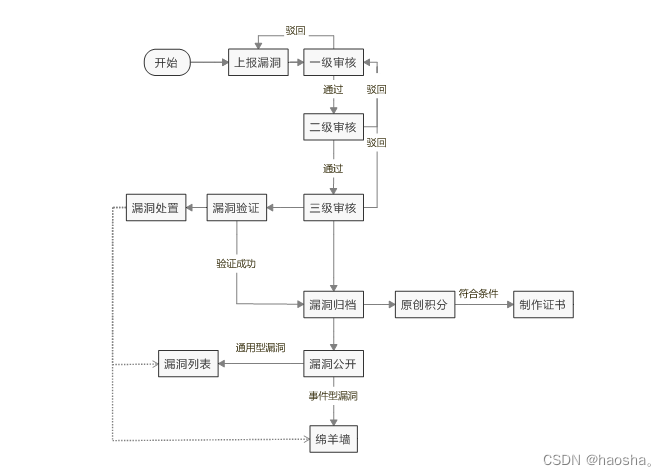
CNVD原创漏洞审核和处理流程
一、CNVD原创漏洞审核归档和发布主流程 (一)审核和归档流程 审核流程分为一级、二级、三级审核,其中一级审核主要对提交的漏洞信息完整性进行审核,漏洞符合可验证(通用型漏洞有验证代码信息或多个互联网实例、事件型…...
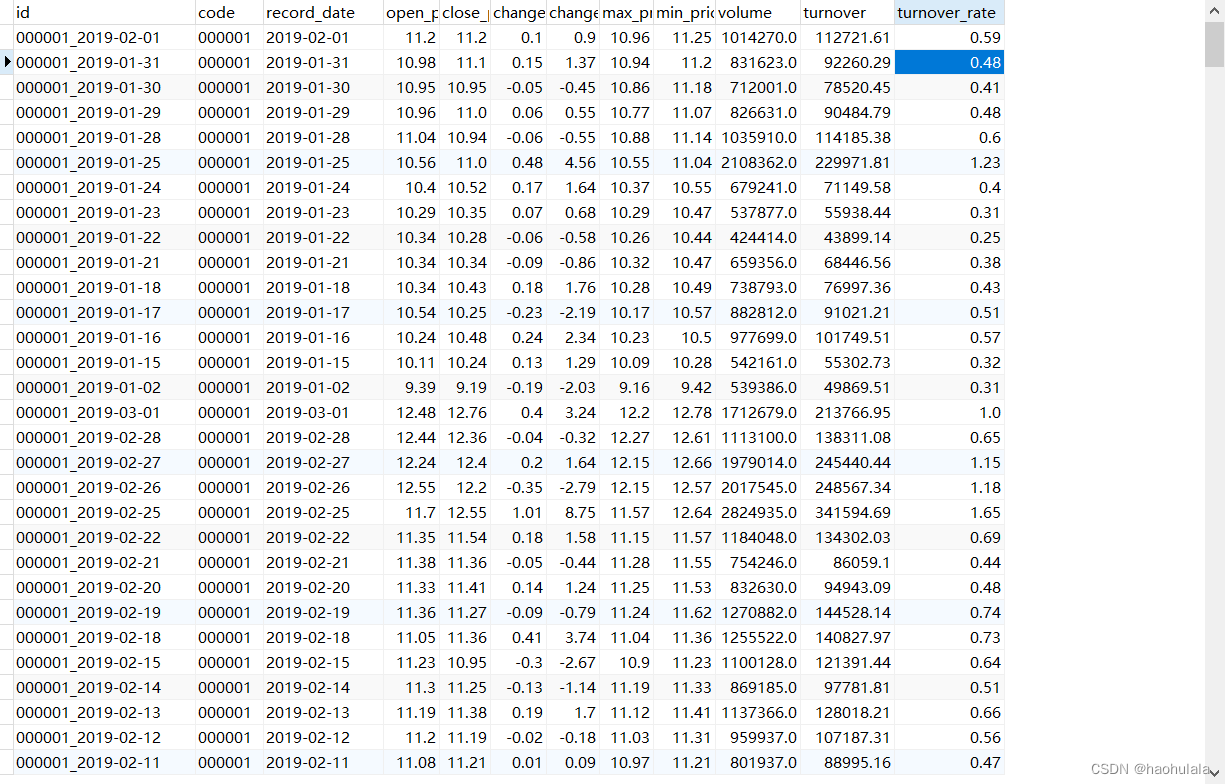
【java爬虫】基于springboot+jdbcTemplate+sqlite+OkHttp获取个股的详细数据
注:本文所用技术栈为:springbootjdbcTemplatesqliteOkHttp 前面的文章我们获取过沪深300指数的成分股所属行业以及权重数据,本文我们来获取个股的详细数据。 我们的数据源是某狐财经,接口的详细信息在下面的文章中,本…...

智能优化算法应用:基于人工兔算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于人工兔算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于人工兔算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.人工兔算法4.实验参数设定5.算法结果6.参考文…...
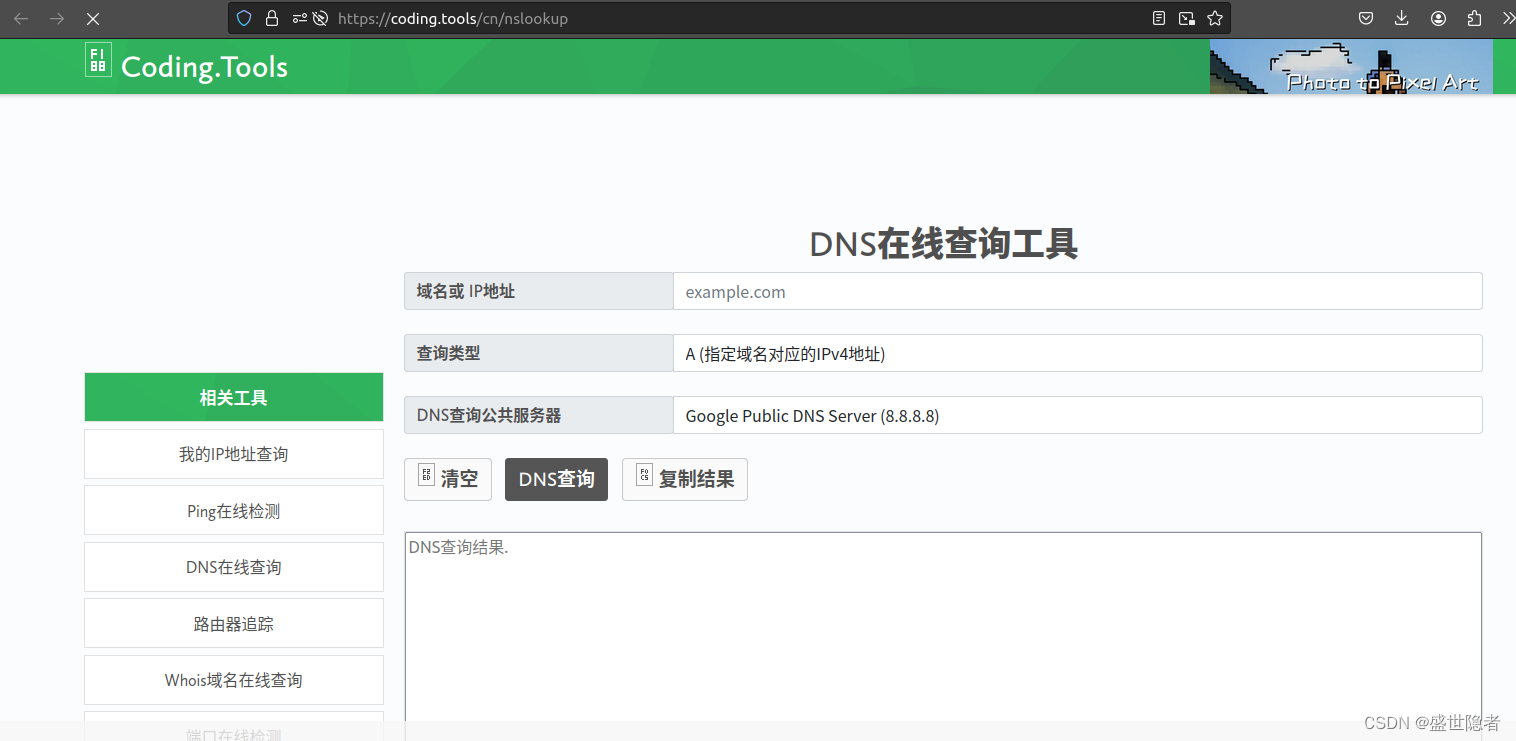
【ubuntu 22.04】安装vscode并配置正常访问应用商店
注意:要去vscode官网下载deb安装包,在软件商店下载的版本不支持输入中文 在ubuntu下用火狐浏览器无法访问vscode官网,此时可以手动进行DNS解析,打开DNS在线查询工具,解析以下主机地址(复制最后一个IP地址&a…...

K8s出现问题时,如何排查解决!
K8s问题的排查 1. POD启动异常、部分节点无法启动pod2. 审视集群状态3. 追踪事件日志4. 聚焦Pod状态5. 检查网络连通性6. 审视存储配置7. 研究容器日志8. K8S集群网络通信9. 问题:Service 是否通过 DNS 工作?10. 总结1、POD启动异常、部分节点无法启动p…...

2015年第四届数学建模国际赛小美赛B题南极洲的平均温度解题全过程文档及程序
2015年第四届数学建模国际赛小美赛 B题 南极洲的平均温度 原题再现: 地表平均温度是反映气候变化和全球变暖的重要指标。然而,在以前的估计中,在如何界定土地平均数方面存在一些方法上的差异。为简单起见,我们只考虑南极洲。请建…...

npm常见错误
三个方面 1. npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! phantomjs-prebuilt2.1.15 install: node install.js npm ERR! Exit status 1 npm ERR! npm ERR! Failed at the phantomjs-prebuilt2.1.15 install script. np…...

JVM入门到入土-Java虚拟机寄存器指令集与栈指令集
JVM入门到入土-Java虚拟机寄存器指令集与栈指令集 HotSpot虚拟机中的任何操作都需要入栈和出栈的步骤。 由于跨平台性的设计,Java的指令都是根据栈来设计的。不同平台CPU架构不同,所以不能设计为基于寄存器的。优点是跨平台,指令集小&#x…...
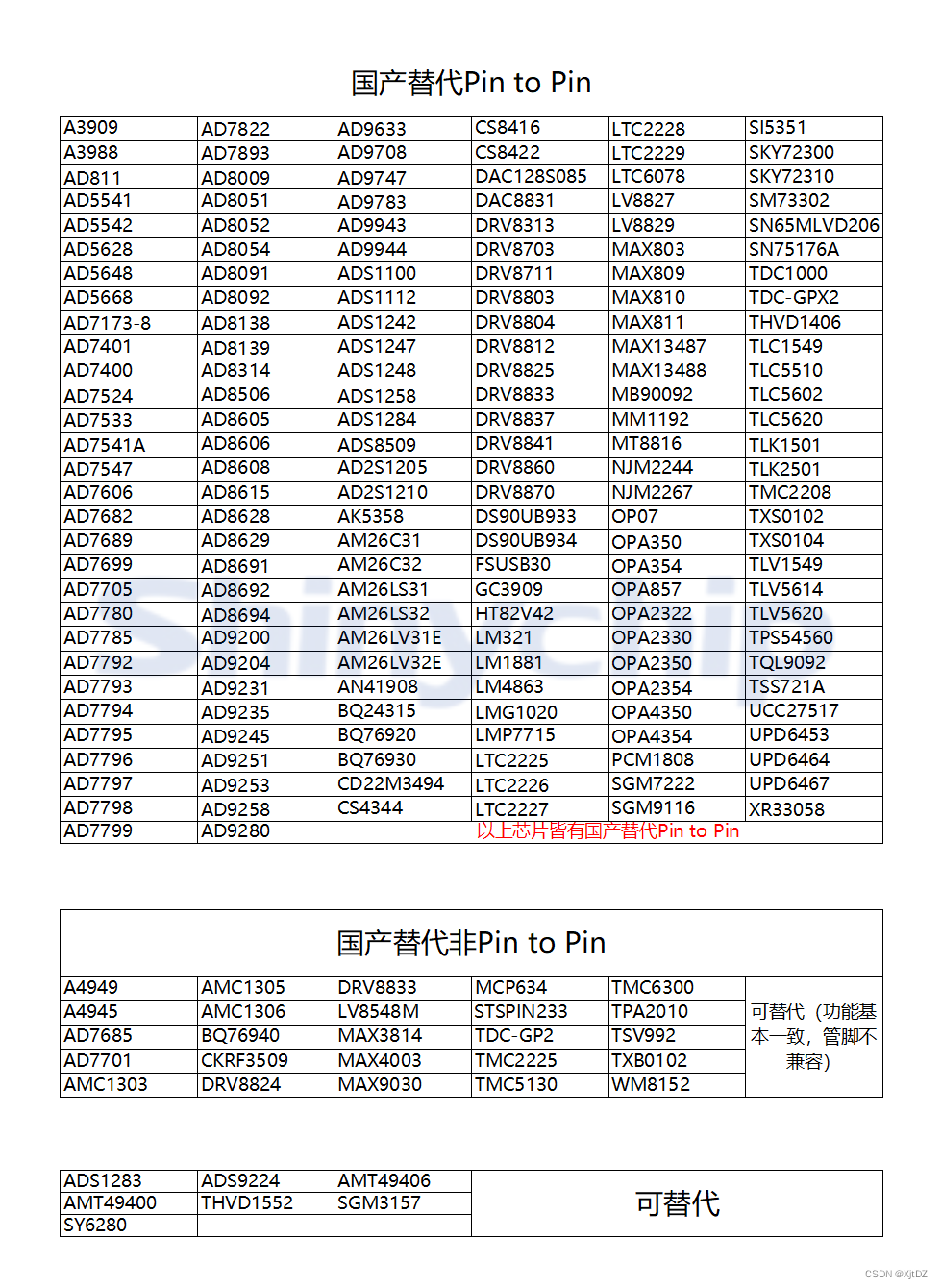
MS2244模拟开关可Pin to Pin兼容NJM2244
MS2244 是一款集成的视频开关,实现三输入视频或音频信号的三选一。可Pin to Pin兼容NJM2244。 芯片集成了 75Ω驱动电路,可以直接驱动电视监控器。芯片工作电压 5V~12V,带宽 10MHz,抗串扰 70dB (4.43MHz)。另外芯片还集…...
PostgreSQL 可观测性最佳实践
简介 软件简述 PostgreSQL 是一种开源的关系型数据库管理系统 (RDBMS),它提供了许多可观测性选项,以确保数据库的稳定性和可靠性。 可观测性 可观测性(Observability)是指对数据库状态和操作进行监控和记录,以便在…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
