二叉搜索树、AVL、红黑树、B树
文章目录
- 二叉搜索树
- 2. avl树
- 3. 红黑树
b树和b+树比较适合与磁盘打交道的，磁盘操作耗时，这些树 矮，红黑树、avL树高，比较适合与内存打交道。
找一个节点的前驱和后继：
前驱：如果节点有左子树，找左子树的最大值，如果没有左子树，找最近一个自右而来的节点
后继：如果节点有右子树，找右子树的最小值，如果没有右子树，找最近一个自左而来的节点
2. avl树
左右子树高度差不超过1
新增和删除节点会导致树的失衡，要进行下面操作
LL
LR
RR
RL
3. 红黑树
红黑树也是一种自平衡的二叉搜索树，较之 AVL，插入和删除时旋转次数更少
红黑树特性
- 所有节点都有两种颜色：红🔴、黑⚫️
- 所有 null 视为黑色⚫️
- 红色🔴节点不能相邻
- 根节点是黑色⚫️
- 从根到任意一个叶子节点，路径中的黑色⚫️节点数一样
插入情况
插入节点均视为红色🔴
case 1：插入节点为根节点，将根节点变黑⚫️
case 2：插入节点的父亲若为黑色⚫️，树的红黑性质不变，无需调整
插入节点的父亲为红色🔴，触发红红相邻
case 3：叔叔为红色🔴
- 父亲变为黑色⚫️，为了保证黑色平衡，连带的叔叔也变为黑色⚫️
- 祖父如果是黑色不变，会造成这颗子树黑色过多，因此祖父节点变为红色🔴
- 祖父如果变成红色，可能会接着触发红红相邻，因此对将祖父进行递归调整
case 4：叔叔为黑色⚫️
- 父亲为左孩子，插入节点也是左孩子，此时即 LL 不平衡
- 让父亲变黑⚫️，为了保证这颗子树黑色不变，将祖父变成红🔴，但叔叔子树少了一个黑色
- 祖父右旋，补齐一个黑色给叔叔，父亲旋转上去取代祖父，由于它是黑色，不会再次触发红红相邻
- 父亲为左孩子，插入节点是右孩子，此时即 LR 不平衡
- 父亲左旋，变成 LL 情况，按 1. 来后续处理
- 父亲为右孩子，插入节点也是右孩子，此时即 RR 不平衡
- 让父亲变黑⚫️，为了保证这颗子树黑色不变，将祖父变成红🔴，但叔叔子树少了一个黑色
- 祖父左旋，补齐一个黑色给叔叔，父亲旋转上去取代祖父，由于它是黑色，不会再次触发红红相邻
- 父亲为右孩子，插入节点是左孩子，此时即 RL 不平衡
- 父亲右旋，变成 RR 情况，按 3. 来后续处理
删除情况
case0：如果删除节点有两个孩子
- 交换删除节点和后继节点的 key，value，递归删除后继节点，直到该节点没有孩子或只剩一个孩子
如果删除节点没有孩子或只剩一个孩子
case 1：删的是根节点
- 删完了，直接将 root = null
- 用剩余节点替换了根节点的 key，value，根节点孩子 = null，颜色保持黑色⚫️不变
删黑色会失衡，删红色不会失衡，但删黑色有一种简单情况
case 2：删的是黑⚫️，剩下的是红🔴，剩下这个红节点变黑⚫️
删除节点和剩下节点都是黑⚫️，触发双黑，双黑意思是，少了一个黑
case 3：被调整节点的兄弟为红🔴，此时两个侄子定为黑 ⚫️
- 删除节点是左孩子，父亲左旋
- 删除节点是右孩子，父亲右旋
- 父亲和兄弟要变色，保证旋转后颜色平衡
- 旋转的目的是让黑侄子变为删除节点的黑兄弟，对删除节点再次递归，进入 case 4 或 case 5
case 4：被调整节点的兄弟为黑⚫️，两个侄子都为黑 ⚫️
- 将兄弟变红🔴，目的是将删除节点和兄弟那边的黑色高度同时减少 1
- 如果父亲是红🔴，则需将父亲变为黑，避免红红，此时路径黑节点数目不变
- 如果父亲是黑⚫️，说明这条路径还是少黑，再次让父节点触发双黑
case 5：被调整节点的兄弟为黑⚫️，至少一个红🔴侄子
- 如果兄弟是左孩子，左侄子是红🔴，LL 不平衡
- 将来删除节点这边少个黑，所以最后旋转过来的父亲需要变成黑⚫️，平衡起见，左侄子也是黑⚫️
- 原来兄弟要成为父亲，需要保留父亲颜色
- 如果兄弟是左孩子，右侄子是红🔴，LR 不平衡
- 将来删除节点这边少个黑，所以最后旋转过来的父亲需要变成黑⚫️
- 右侄子会取代原来父亲，因此它保留父亲颜色
- 兄弟已经是黑了⚫️，无需改变
- 如果兄弟是右孩子，右侄子是红🔴，RR 不平衡
- 将来删除节点这边少个黑，所以最后旋转过来的父亲需要变成黑⚫️，平衡起见，右侄子也是黑⚫️
- 原来兄弟要成为父亲，需要保留父亲颜色
- 如果兄弟是右孩子，左侄子是红🔴，RL 不平衡
- 将来删除节点这边少个黑，所以最后旋转过来的父亲需要变成黑⚫️
- 左侄子会取代原来父亲，因此它保留父亲颜色
- 兄弟已经是黑了⚫️，无需改变
相关文章：
二叉搜索树、AVL、红黑树、B树
文章目录 二叉搜索树2. avl树3. 红黑树 b树和b树比较适合与磁盘打交道的，磁盘操作耗时，这些树 矮，红黑树、avL树高，比较适合与内存打交道。 二叉搜索树 找一个节点的前驱和后继： 前驱：如果节点有左子树&a…...
格密码：傅里叶矩阵
目录 一. 铺垫性介绍 1.1 傅里叶级数 1.2 傅里叶矩阵的来源 二. 格基与傅里叶矩阵 2.1 傅里叶矩阵详细解释 2.2 格基与傅里叶矩阵 写在前面：有关傅里叶变换的解释太多了，这篇博客主要总结傅里叶矩阵在格密码中的运用。对于有一定傅里叶变换基础的同…...
flex--伸缩性
1.flex-basis flex-basis 设置的是主轴方向的基准长度，会让宽度或高度失效。 备注：主轴横向：宽度失效；主轴纵向：高度失效 作用：浏览器根据这个属性设置的值，计算主轴上是否有多余空间&#x…...
linux中主从复制的架构和读写分离的方式
读写分离 互相主从架构注意点 双主双从架构注意点 一主多从架构注意点 读写分离概念部署jdk环境上传文件，解压文件配置环境变量 部署mycat环境mycat配置文件给所有数据库创建访问用户配置 server.xml配置 schema.xml启动mycat查看启动端口日志负载均衡测试 遇到的问…...
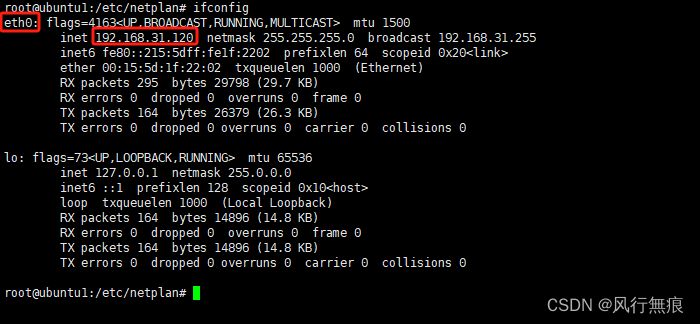
Ubuntu 22.04.3 Server 设置静态IP 通过修改yaml配置文件方法
目录 1.查看网卡信息 2.修改yaml配置文件 3.应用新的网络配置 4.重新启动网络服务 文章内容 本文介绍Ubuntu 22.04.3 Server系统通过修改yaml配置文件配置静态 ip 的方法。 1.查看网卡信息 使用ifconfig命令查看网卡信息获取网卡名称 如果出现Command ifconfig not fo…...
EasyCVR无人机推流+人数统计AI算法，助力公共场所人群密度管控
一、背景与需求 在公共场所和大型活动的管理中，人数统计和人群密度控制是非常重要的安全问题。传统的方法可能存在效率低下或准确度不足的情况，无法满足现代社会的需求。TSINGSEE青犀可以利用无人机推流AI人流量统计算法，基于计算机视觉技术…...
Kotlin 接口
Kotlin 的接口可以既包含抽象方法的声明也包含实现；接口无法保存状态；可以有属性但必须声明为抽象或提供访问器实现 1、定义 使用关键字 interface 来定义接口 interface MyInterface {fun bar()fun foo() {// 可选的方法体} } 2、 实现接口 一个类…...
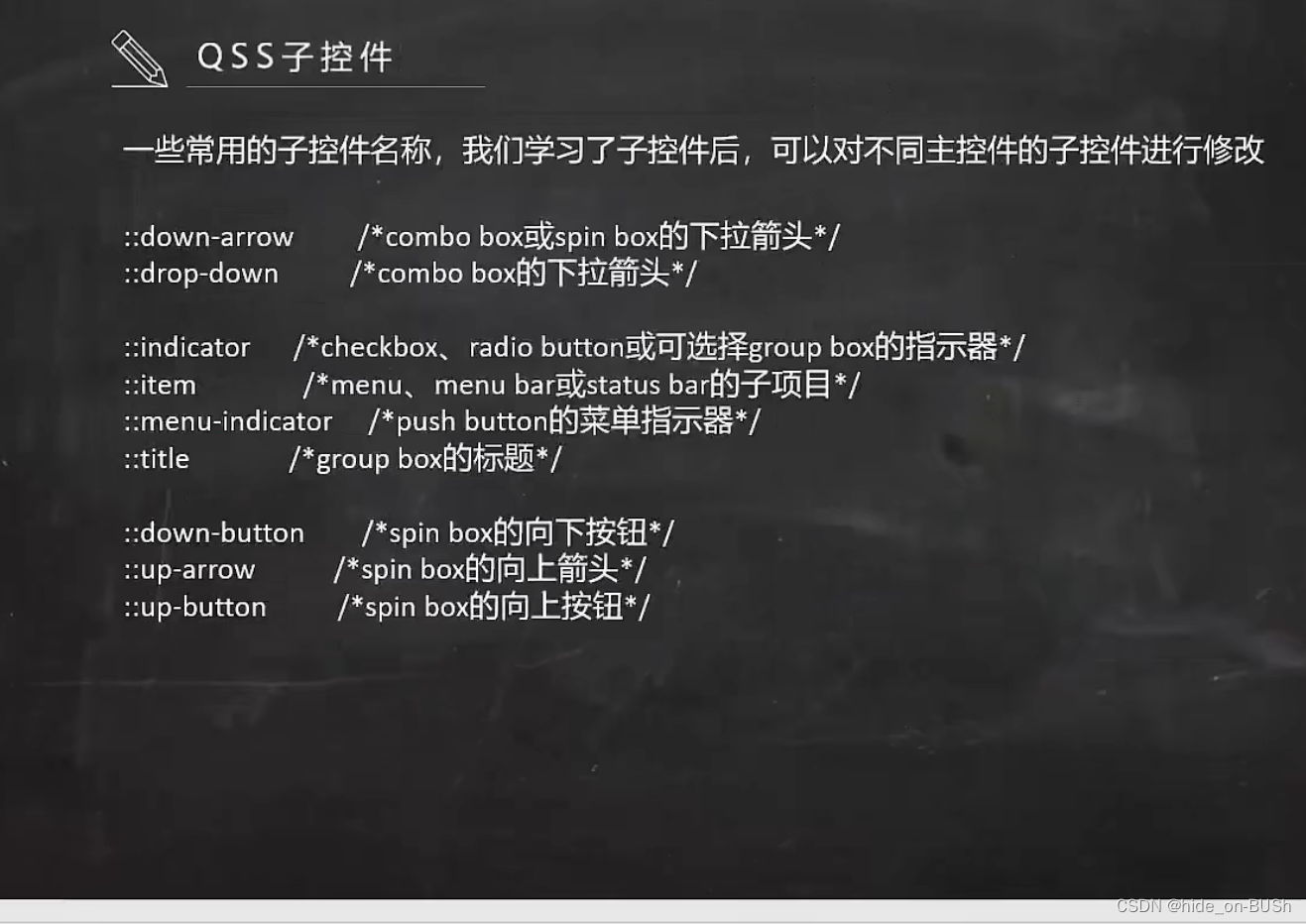
Qt前端技术：5.QSS
这个是表示QFrame中的pushButton中的子类和它子类的子类都将背景变为red 写成大于的时候表示只有直接的子类对象才会变 这个图中的QGroupBox和QPushButton都是QFrame的直接的子类 这个中的QGroupBox是QFrame的直接的子类但是QPushButton 是QGroupBox的子类，QPushB…...
在Centos7中利用Shell脚本：实现MySQL的数据备份
目录 自动化备份MySQL 一.备份数据库脚本 1.创建备份目录 2.创建脚本文件 3.新建配置文件（连接数据库的配置文件） 4.给文件权限(mysql_backup.sh) 编辑 5.执行命令 (mysql_backup.sh) 编辑 二.数据库通过备份恢复 1.创建脚…...
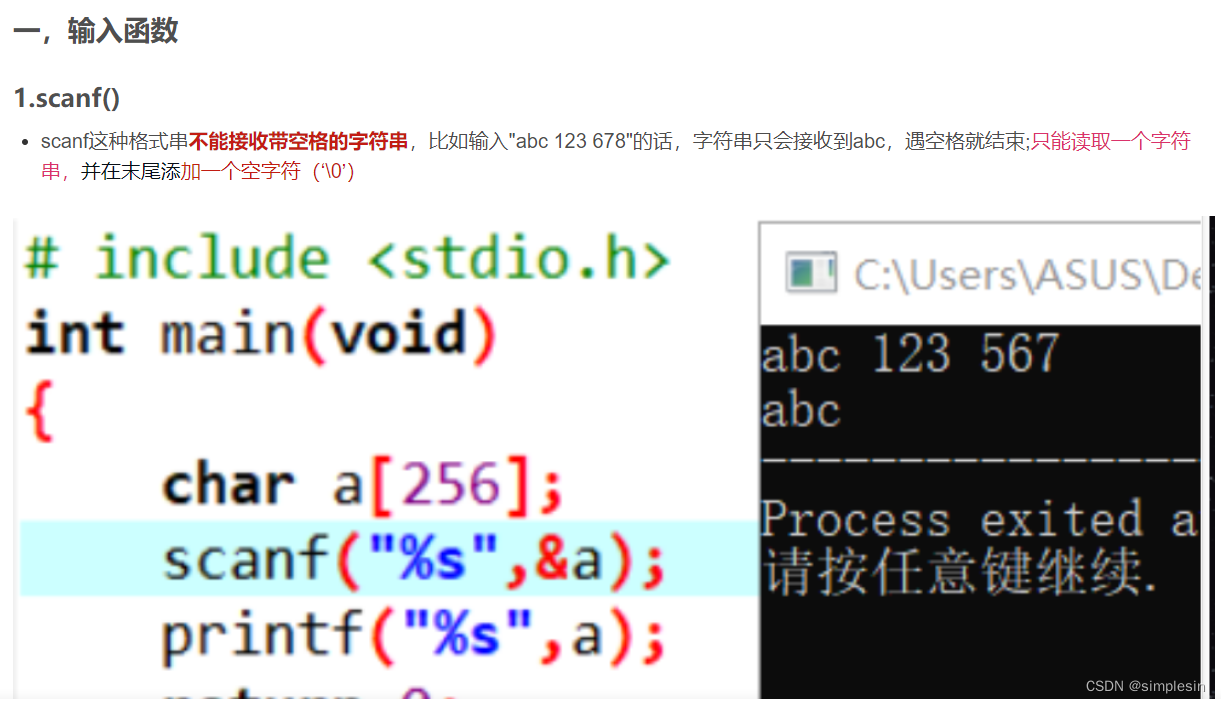
大一C语言查缺补漏 12.24
遗留问题： 6-1 1 在C语言中，如果要保留小数的话，一定要除以2.0，而不是2。 设整型变量m,n,a,b的值均为1，执行表达式（m a>b）||(n a<b)后，表达式的值以及变量m和n的值是&#…...
程序员宝典：常用的免费好物API
六位图片验证码生成：包括纯数字、小写字母、大写字母、大小写混合、数字小写、数字大写、数字大小写等情况。 四位图片验证码生成：四位图片验证码生成，包括纯数字、小写字母、大写字母、大小写混合、数字小写、数字大写、数字大小写等情况。…...
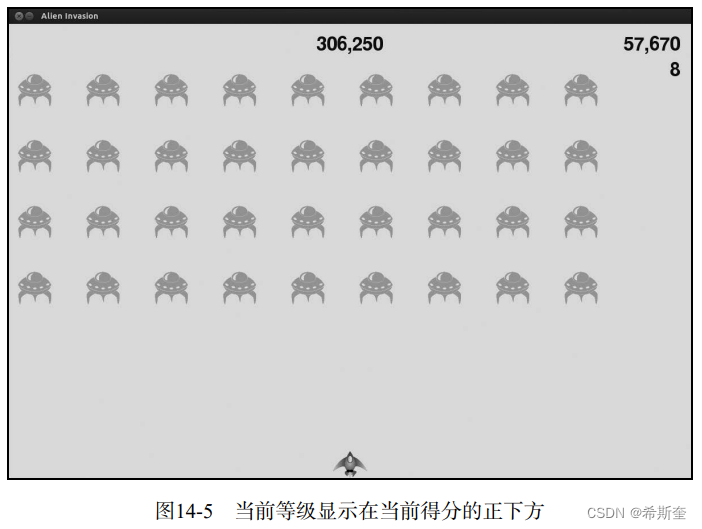
关于“Python”的核心知识点整理大全41
目录 scoreboard.py game_functions.py game_functions.py 14.3.8 显示等级 game_stats.py scoreboard.py scoreboard.py scoreboard.py game_functions.py game_functions.py alien_invasion.py 14.3.9 显示余下的飞船数 ship.py scoreboard.py 我们将最高得分圆整…...
java进阶(二)-java小干货
java一些精干知识点分享 2. java小干货2.1循环遍历2.2可变参数2.3 list和数组转化2.3.1 数组转list2.3.2 list转数组 2.4 值传递和地址传递2.4.1值传递2.4.2 地址传递2.4.3易错点总结 2.5 数据类型2.5.1基础知识2.5.2 基础数据和包装类 2.6 字符串2.6.1 char/String区别2.6.2 .…...
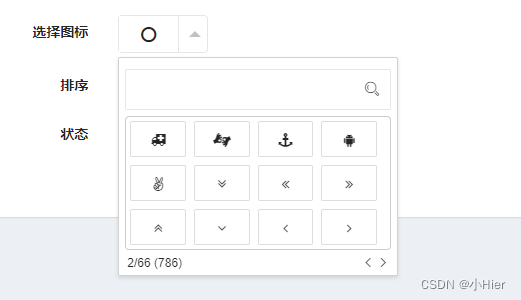
layui（iconPickerFa）图标选择器插件，主要用于后台菜单图标管理
话不多说直接上代码 在页面中引入如下代码 <link rel"stylesheet" href"/template/admin/layui-v2.5.6/css/layui.css"> <script type"text/javascript" src"/template/admin/layui-v2.5.6/layui.js"></script> &…...
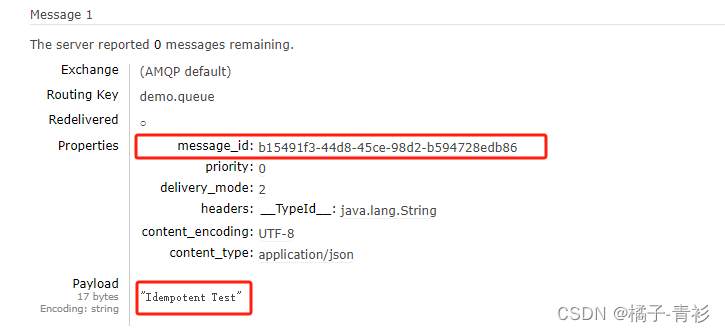
RabbitMQ入门指南(九)：消费者可靠性
专栏导航 RabbitMQ入门指南 从零开始了解大数据 目录 专栏导航 前言 一、消费者确认机制 二、失败重试机制 三、失败处理策略 四、业务幂等性 1.通过唯一标识符保证操作的幂等性 2.通过业务判断保证操作的幂等性 总结 前言 RabbitMQ是一个高效、可靠的开源消息队列系…...
MySQL的聚合函数、MySQL的联合查询、MySQL的左连接右连接内连接
MySQL的聚合函数 MySQL聚合函数是在数据库中对数据进行聚合操作的函数。它们将多行数据作为输入，并返回单个值作为结果。 常用的MySQL聚合函数包括： COUNT：计算符合条件的行数。SUM：对指定列的数值进行求和操作。AVG࿱…...
RKNN Toolkit Lite2 一键安装和测试，sh脚本
RKNN Toolkit Lite2 安装和测试教程 本教程旨在指导用户如何使用提供的shell脚本来安装和测试RKNN Toolkit Lite2，适用于需要在Linux系统上部署和测试AI模型的开发者。 简介 RKNN Toolkit Lite2是一个高效的AI模型转换和推理工具包，专为Rockchip NPU设…...
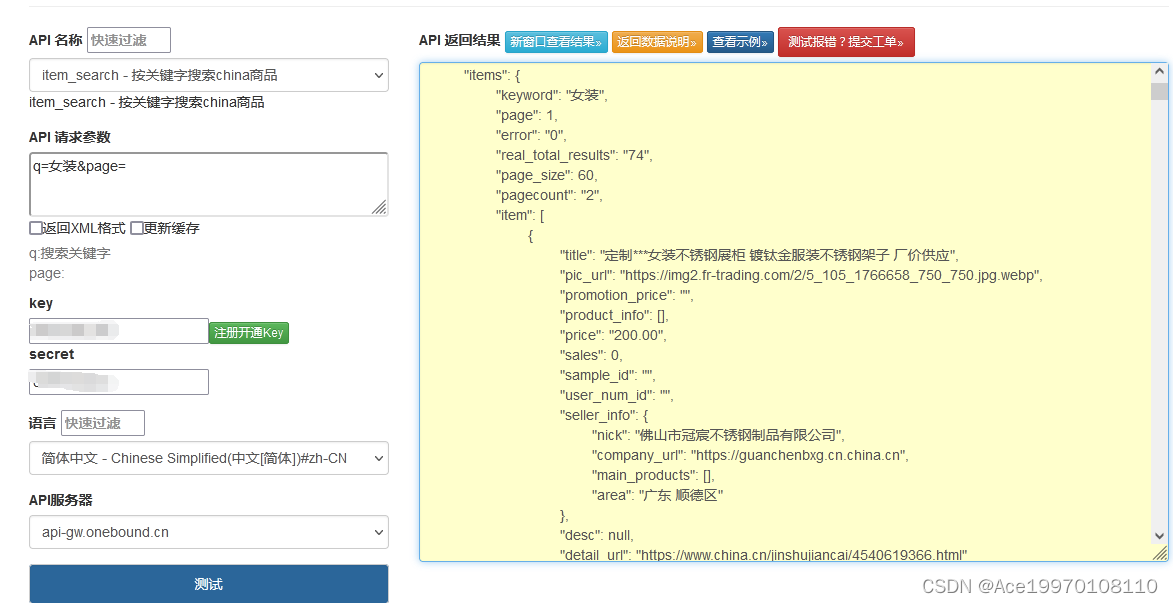
探索中国制造API接口：解锁无限商机，引领制造业数字化转型
一、概述 中国制造API接口是一种应用程序接口，专门为中国制造行业提供数据和服务。通过使用API接口，开发者可以轻松地获取中国制造的商品信息、供应商数据、生产能力等，从而为他们的应用程序或网站提供更加丰富的内容和功能。 二、API接口的…...
CentOS上安装MySQL 8.0的详细教程
CentOS上安装MySQL 8.0的详细教程 大家好，我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编，也是冬天不穿秋裤，天冷也要风度的程序猿！今天我将为大家分享一篇关于在CentOS上安装MySQL 8.0的详细教程。MySQL是一个强大…...
[RISCV] 为android14添加一个新的riscv device
本篇博客将基于android-14-r18添加Sifive unmatched板子的支持。 Setup build envoronment Establishing a build environment $ sudo apt install git-core gnupg flex bison build-essential zip curl zlib1g-dev libc6-dev-i386 libncurses5 x11proto-core-dev libx11-de…...
iPhone密码忘记了办？iPhoneUnlocker，iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候，难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵，或者买了二手 iPhone 却被原来的 iCloud 账号锁住，这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...
Auto-Coder使用GPT-4o完成：在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库，获取股票数据，并生成TabPFN这个模型 可以识别、处理的格式，写一个完整的预处理示例，并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务，进行预测并输…...
如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时，你可能需要保留重要的数据，例如通讯录。好在，将通讯录从 iPhone 转移到 Android 手机非常简单，你可以从本文中学习 6 种可靠的方法，确保随时保持连接，不错过任何信息。 第 1…...
【AI学习】三、AI算法中的向量
在人工智能（AI）算法中，向量（Vector）是一种将现实世界中的数据（如图像、文本、音频等）转化为计算机可处理的数值型特征表示的工具。它是连接人类认知（如语义、视觉特征）与…...
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码： prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程，代码下载：这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中，**知识蒸馏（Knowledge Distillation）**被广泛应用，作为提升模型…...
招商蛇口 | 执笔CID，启幕低密生活新境
作为中国城市生长的力量，招商蛇口以“美好生活承载者”为使命，深耕全球111座城市，以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子，招商蛇口始终与城市发展同频共振，以建筑诠释对土地与生活的…...
Go 并发编程基础：通道（Channel）的使用
在 Go 中，Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式，用于在多个 Goroutine 之间传递数据，从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
RabbitMQ入门4.1.0版本（基于java、SpringBoot操作）
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发，后来由Pivotal Software Inc.（现为VMware子公司）接管。RabbitMQ 是一个开源的消息代理和队列服务器，用 Erlang 语言编写。广泛应用于各种分布…...
C#学习第29天：表达式树（Expression Trees）
目录 什么是表达式树？ 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持： 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...