layui(iconPickerFa)图标选择器插件,主要用于后台菜单图标管理
话不多说直接上代码
在页面中引入如下代码
<link rel="stylesheet" href="/template/admin/layui-v2.5.6/css/layui.css">
<script type="text/javascript" src="/template/admin/layui-v2.5.6/layui.js"></script>
<script type="text/javascript" src="/template/admin/iconPicker/iconPickerFa.js"></script>第二步html页面如图
<div class="form-group"><label class="col-sm-2 control-label">选择图标</label><div class="col-sm-3"><input type="text" id="icon" name="menu[icon]" lay-filter="icon" class="hide" value="fa fa-list"></div>
</div>第三步如图代码
<script>layui.use(['form', 'upload', 'jquery','table'], function() {var form = layui.form,upload = layui.upload,iconPickerFa = layui.iconPickerFa,$ = layui.jquery;var table = layui.table;var iconLess="/template/admin/font-awesome-4.7.0/less/variables.less"iconPickerFa.render({elem: '#icon',url: iconLess,limit: 12,click: function (data) {$('#icon').val('fa ' + data.icon);},success: function (d) {console.log(d);}});})
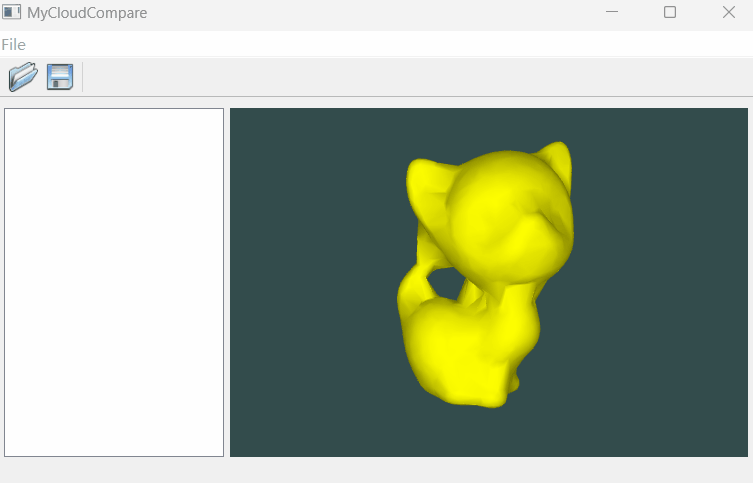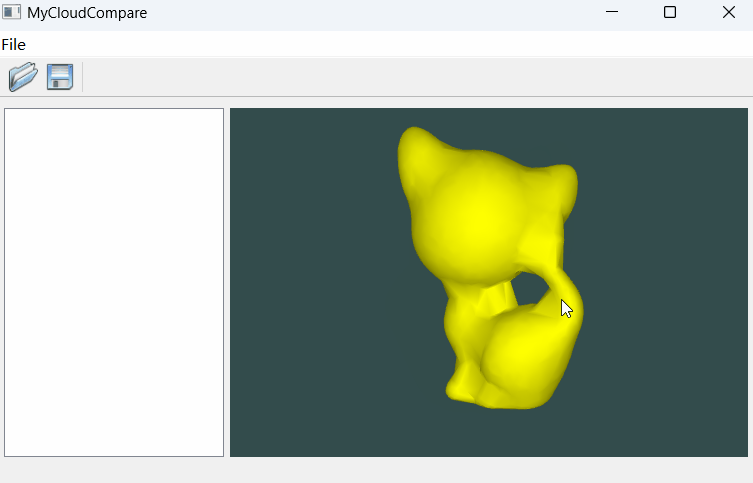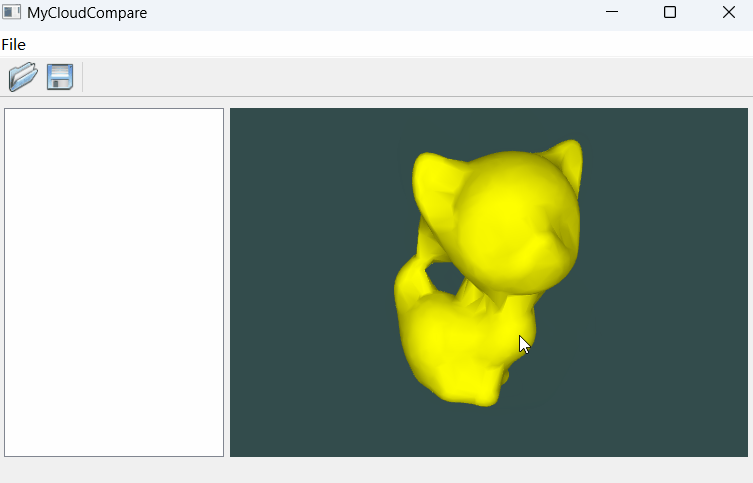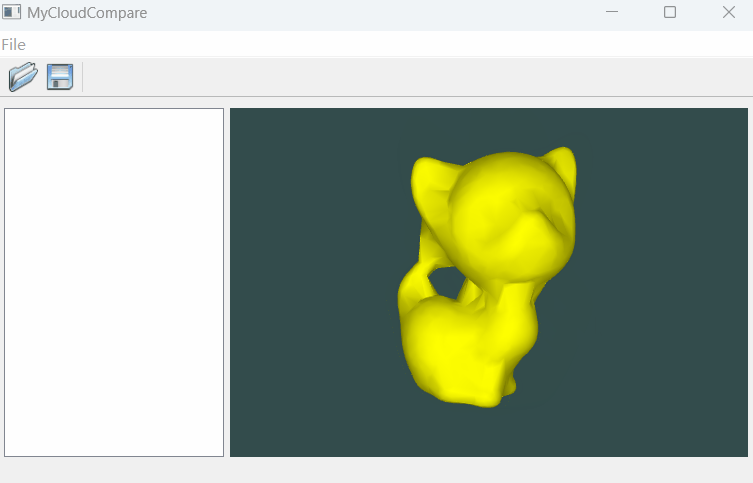
</script>最终呈现如下图
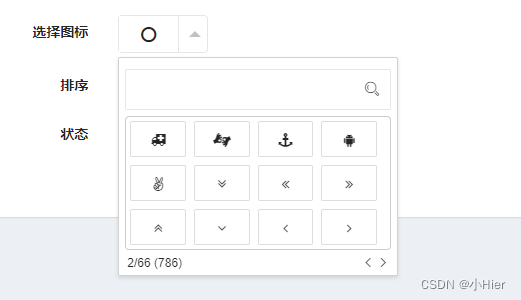
layui iconPicker插件下载地址
相关文章:

layui(iconPickerFa)图标选择器插件,主要用于后台菜单图标管理
话不多说直接上代码 在页面中引入如下代码 <link rel"stylesheet" href"/template/admin/layui-v2.5.6/css/layui.css"> <script type"text/javascript" src"/template/admin/layui-v2.5.6/layui.js"></script> &…...
RabbitMQ入门指南(九):消费者可靠性
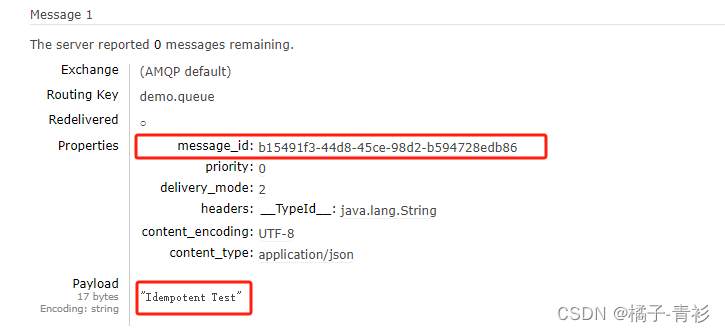
专栏导航 RabbitMQ入门指南 从零开始了解大数据 目录 专栏导航 前言 一、消费者确认机制 二、失败重试机制 三、失败处理策略 四、业务幂等性 1.通过唯一标识符保证操作的幂等性 2.通过业务判断保证操作的幂等性 总结 前言 RabbitMQ是一个高效、可靠的开源消息队列系…...

MySQL的聚合函数、MySQL的联合查询、MySQL的左连接右连接内连接
MySQL的聚合函数 MySQL聚合函数是在数据库中对数据进行聚合操作的函数。它们将多行数据作为输入,并返回单个值作为结果。 常用的MySQL聚合函数包括: COUNT:计算符合条件的行数。SUM:对指定列的数值进行求和操作。AVG࿱…...

RKNN Toolkit Lite2 一键安装和测试,sh脚本
RKNN Toolkit Lite2 安装和测试教程 本教程旨在指导用户如何使用提供的shell脚本来安装和测试RKNN Toolkit Lite2,适用于需要在Linux系统上部署和测试AI模型的开发者。 简介 RKNN Toolkit Lite2是一个高效的AI模型转换和推理工具包,专为Rockchip NPU设…...
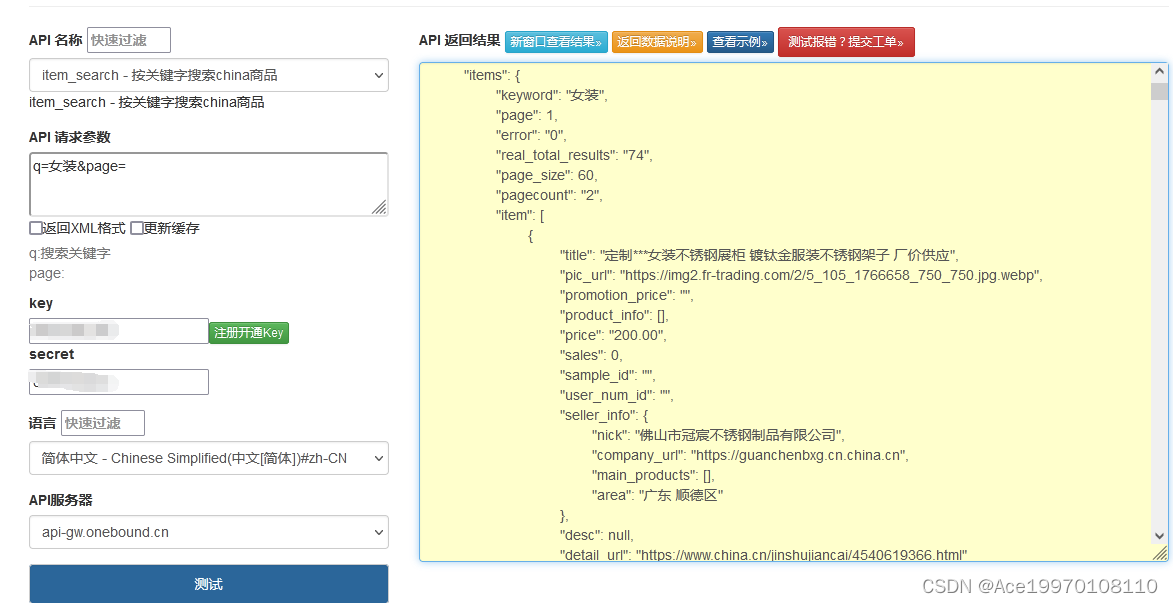
探索中国制造API接口:解锁无限商机,引领制造业数字化转型
一、概述 中国制造API接口是一种应用程序接口,专门为中国制造行业提供数据和服务。通过使用API接口,开发者可以轻松地获取中国制造的商品信息、供应商数据、生产能力等,从而为他们的应用程序或网站提供更加丰富的内容和功能。 二、API接口的…...

CentOS上安装MySQL 8.0的详细教程
CentOS上安装MySQL 8.0的详细教程 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我将为大家分享一篇关于在CentOS上安装MySQL 8.0的详细教程。MySQL是一个强大…...

[RISCV] 为android14添加一个新的riscv device
本篇博客将基于android-14-r18添加Sifive unmatched板子的支持。 Setup build envoronment Establishing a build environment $ sudo apt install git-core gnupg flex bison build-essential zip curl zlib1g-dev libc6-dev-i386 libncurses5 x11proto-core-dev libx11-de…...
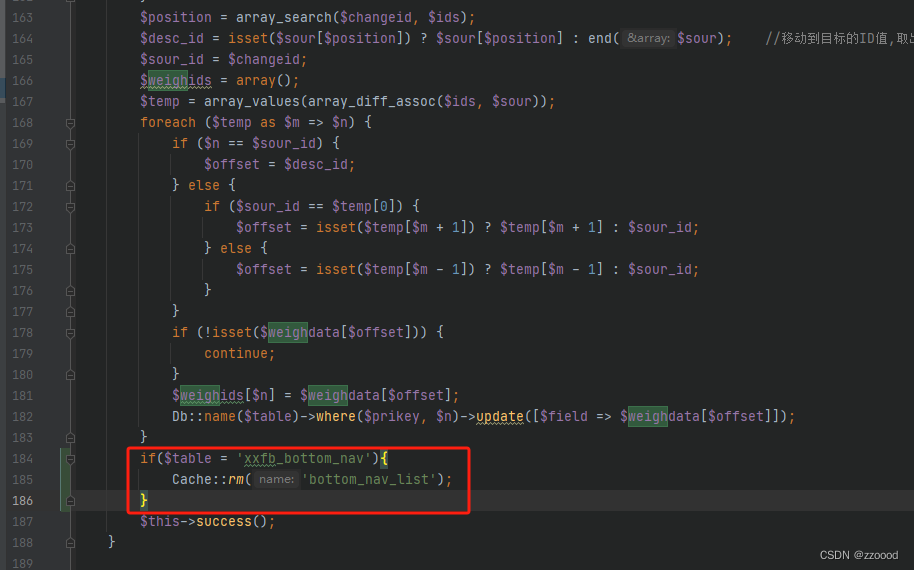
【Fastadmin】通用排序weigh不执行model模型的事件
在model模型类支持的before_delete、after_delete、before_write、after_write、before_update、after_update、before_insert、after_insert事件行为中,我们可以快捷的做很多操作,如删除缓存、逻辑判断等 但是在fastadmin的通用排序weigh拖动中无法触发…...
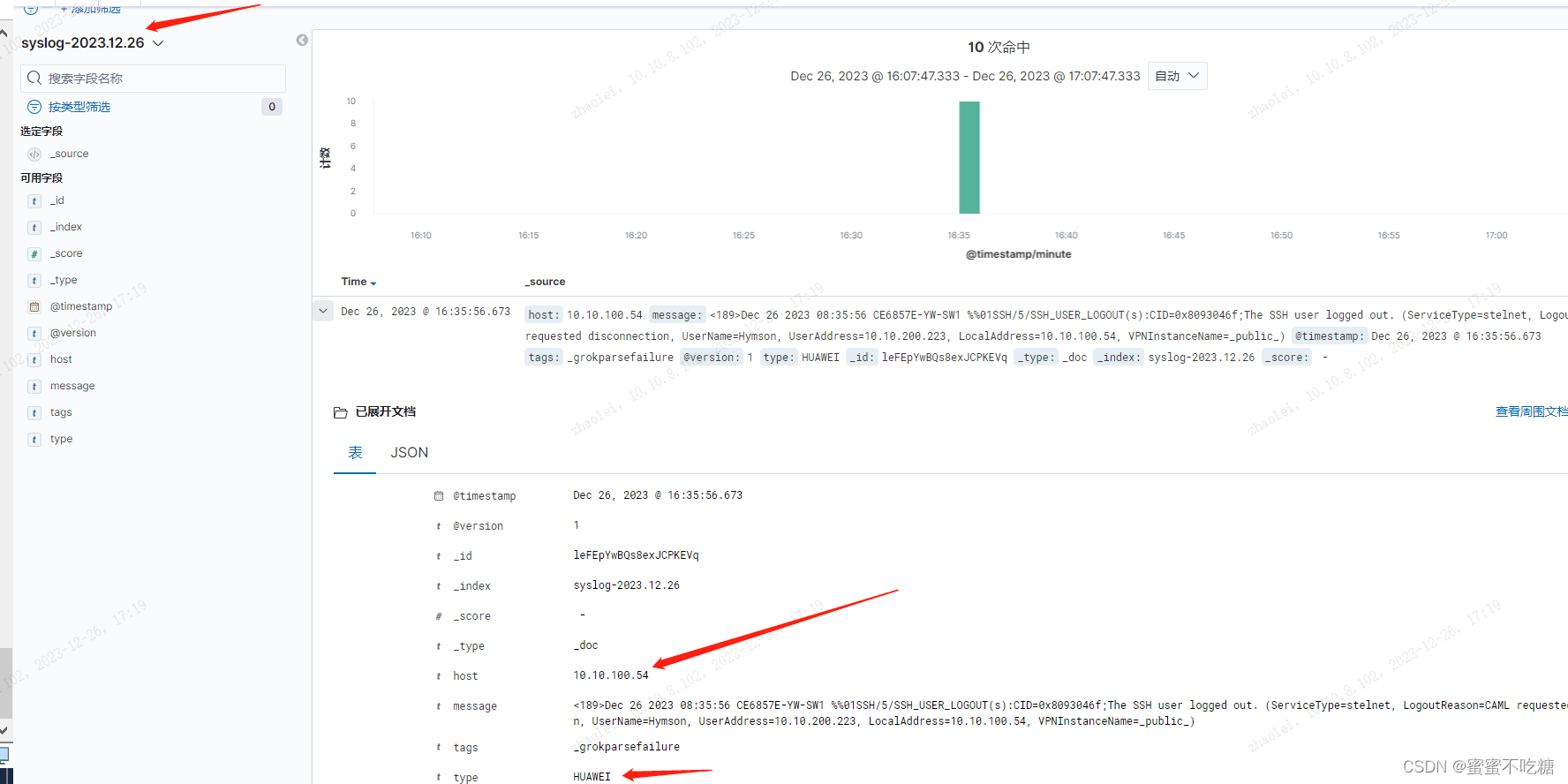
logstash收集华为、H3C、Cisco交换机日志
网络设备配置 将 syslog-ip 替换成服务器的IP地址。 Huawei info-center loghost source interface info-center loghost syslog-ip local-time facility local6 H3C info-center loghost source interface info-center loghost syslog-ip facility local5 Aruba logging arm …...

云上荆楚丨云轴科技ZStack成功实践精选(湖北)
湖北自古以来有九省通衢的美称,地处长江中游,富有荆楚之美誉,灵秀之蕴意。2022年湖北数字经济强省三年行动计划正式印发,计划到“十四五”末,数字经济核心产业增加值力争达到7000亿元,占GDP的比重超过12%。…...

C语言字符串处理提取时间(ffmpeg返回的时间字符串)
【1】需求 需求:有一个 “00:01:33.90” 这样格式的时间字符串,需要将这个字符串的时间值提取打印出来(提取时、分、秒、毫秒)。 这个时间字符串从哪里来的? 是ffmpeg返回的时间,也就是视频的总时间。 下…...

NC(65)元数据增加字段
以报销单主表er_bxzb表为例,增加15个字段字段以及两个其他业务所需字段 1、先在er_bxzb增加字段 增加字段 alter table er_bxzb add no_invoice char(1) default(N);alter table er_bxzb add is_enabled_taxation_cloud char(1) default(N);alter table er_bxzb a…...
SParC数据集介绍
导语 SParC是Text-to-SQL领域的一个多轮查询数据集。本篇博客将对该数据集论文和数据格式进行简要介绍。 SParC数据集概述 SParC是一个跨领域的多轮Text-to-SQL数据集。它包含有4298个问题轮次,大约有12k的自然语言问句到SQL标注的Question-SQL对。这些问题来自于…...
OpenGL 绘制Mesh数据(Qt)
文章目录 一、简介二、实现代码三、实现效果一、简介 Mesh数据的结构主要就是点与三角面片,因此本质上仍然是对三角面片进行绘制。这里我们借助VCG这个库实现对Mesh数据的读取,这个库相对简单轻巧,很方便使用。 二、实现代码 由于修改的部分很多,我们逐一进行解释一下: --…...

9.传统的轨道画线算法()
轨道画线分为以下步骤: 1.读取摄像头图片 2.图片灰度处理,截取轨道区域的图片 3.中值滤波处理,并区域取均值后做期望差的绝对值。本人通过一些轨道图片实验,用这种方法二值化得到的效果比caany算子等方法的效果好 4.二值化后再…...
 : B DS二叉排序树_有效的二叉排序树)
F (1164) : B DS二叉排序树_有效的二叉排序树
Description 给你一个二叉树,判断其是否是一个有效的二叉排序树。 有效的二叉排序树定义如下: 1. 结点的左子树只包含小于当前结点的数。 2. 结点的右子树只包含大于当前结点的数。 3. 所有左子树和右子树自身必须也是二叉排序树。 Input 第一行输…...

结合el-upload修改支持上传图片、视频并预览
结合element plus的el-upload标签,实现上传图片和视频,并支持在线预览和放大 1、html部分 <el-form-item label"活动照片、视频"><el-uploadv-model:file-list"state.photoList":action"state.uploadUrl"accept…...
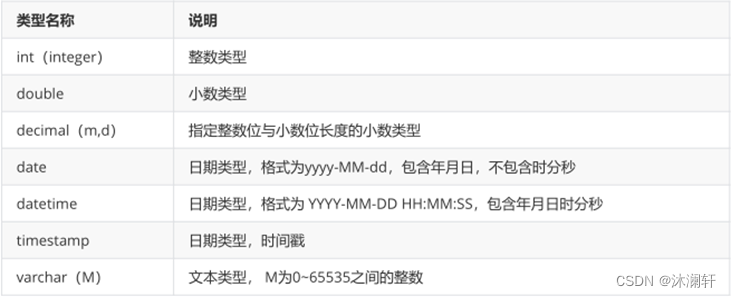
1.SQL - 概述
1. SQL语句分类 • 数据定义语言:简称DDL(Data Definition Language),用来定义数据库对象:数据库,表,列等。关键字:create,alter,drop等 • 数据操作语言:简称DML(Data …...

GaussDB数据库表创建行访问控制策略
目录 一、前言 二、GaussDB中的行访问控制 1、CREATE ROW LEVEL SECURITY POLICY语法 2、ALTER ROW LEVEL SECURITY POLICY语法 3、ROW LEVEL SECURITY策略与适配SQL语法关系 三、GaussDB中的行访问控制策略示例 1、实现GaussDB行访问控制的一般步骤 2、行访问控制策略…...

提升设备巡检效率的关键:易点易动设备管理系统的应用
随着互联网技术的发展,智慧设备管理已成为各行各业提升运营效率的重要选择。相比传统的手动巡检方式,采用设备管理系统可以实现物联网技术给企业带来更高效的运营方式。其中,易点易动作为一款成熟的设备管理系统,其广泛应用于提升设备巡检效率这一领域发挥了很好的作用。 采用易…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
