【三】【C语言\动态规划】珠宝的最高价值、下降路径最小和、最小路径和,三道题目深度解析
动态规划
动态规划就像是解决问题的一种策略,它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题,并将每个小问题的解保存起来。这样,当我们需要解决原始问题的时候,我们就可以直接利用已经计算好的小问题的解,而不需要重复计算。
动态规划与数学归纳法思想上十分相似。
数学归纳法:
-
基础步骤(base case):首先证明命题在最小的基础情况下成立。通常这是一个较简单的情况,可以直接验证命题是否成立。
-
归纳步骤(inductive step):假设命题在某个情况下成立,然后证明在下一个情况下也成立。这个证明可以通过推理推断出结论或使用一些已知的规律来得到。
通过反复迭代归纳步骤,我们可以推导出命题在所有情况下成立的结论。
动态规划:
-
状态表示:
-
状态转移方程:
-
初始化:
-
填表顺序:
-
返回值:
数学归纳法的基础步骤相当于动态规划中初始化步骤。
数学归纳法的归纳步骤相当于动态规划中推导状态转移方程。
动态规划的思想和数学归纳法思想类似。
在动态规划中,首先得到状态在最小的基础情况下的值,然后通过状态转移方程,得到下一个状态的值,反复迭代,最终得到我们期望的状态下的值。
接下来我们通过三道例题,深入理解动态规划思想,以及实现动态规划的具体步骤。
LCR 166. 珠宝的最高价值

题目解析

状态表示
我们可以定义dp[i][j]表示,从(0,0)位置出发,到达(i,j)位置,在所有的可能路径中,所能获得的最大价值数。
状态转移方程
要到达(i,j)位置,要么从(i,j-1)位置往右走一步,要么从(i-1,j)位置往下走一步。根据状态表示,dp[i][j]表示从(0,0)位置出发,到达(i,j)位置,在所有的可能路径中,所能获得的最大价值数。dp[i][j-1]表示从(0,0)位置出发,到达(i,j-1)位置,在所有的可能路径中,所能获得的最大价值数。dp[i-1][j]表示从(0,0)位置出发,到达(i-1,j)位置,在所有的可能路径中,所能获得的最大价值数。
很简单可以得到dp[i][j]=max(dp[i][j-1],dp[i-1][j])+frame[i][j]
在这两种情况下,选择一个更大的价值,再加上自己位置上的价值,就是从(0,0)到达(i,j)位置的最大价值,也就是dp[i][j]
故,状态转移方程为:
dp[i][j]=max(dp[i][j-1],dp[i-1][j])+frame[i][j]
初始化
在填表的过程中,为了不造成越界访问的情况,我们需要对数组中某一些位置进行初始化。根据状态转移方程我们知道,如果要推导出(i,j)位置的状态,我们需要知道(i-1,j)和(i,j-1)位置的状态,所以在数组的第一行和第一列中,如果我们要推导这些状态,就会造成越界访问,所以需要对这些位置上的值进行初始化。
初始化具体操作是根据状态表示定义,依次填写正确的状态。
dp[i][j]表示,从(0,0)位置出发,到达(i,j)位置,在所有的可能路径中,所能获得的最大价值数。
所以第一行中,第一个数填自己的价值,第二个数填前一个数的价值加上自己的价值,以此类推,第一列同理。
我们会发现这样初始化会非常的复杂。
我们能不能把这些位置的计算通过状态转移方程进行推导得出来呢?如果直接进行推导数组一定会造成越界访问的错误,但我们依旧有办法可以把所有状态统一用状态转移方程推导出来,同时也不会造成越界访问的错误。
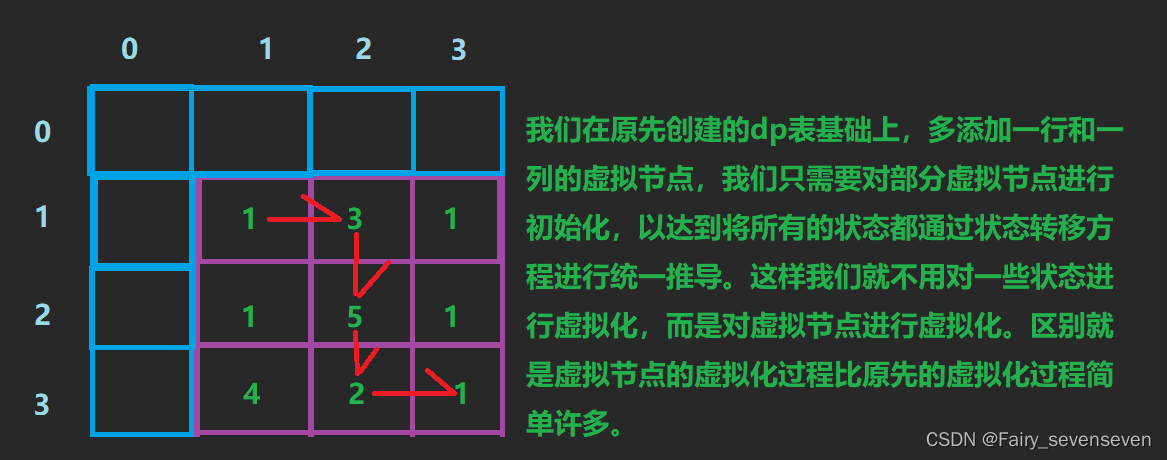
如果我们创建虚拟节点,将所有状态用状态转移方程进行推导,我们只需要初始化虚拟节点就可以了,这样做的好处是,对虚拟节点的初始化过程是十分简便的。
不过创建虚拟节点的操作有几点需要注意。
第一,对虚拟节点的初始化,必须能使所有状态正确推导。
第二,状态表示和状态转移方程需要改变对应关系。
意思是,dp[i][j]对应的位置在frame实际上是[i-1]j-1]位置。需要注意对应关系的改变。
接下来我们对虚拟节点进行初始化。
根据状态转移方程我们知道,(i,j)的状态需要由(i,j-1)(i-1,j)两个位置的状态推导得到,所以我们需要对虚拟节点除(0,0)位置外,每一个值都进行初始化。
因为(1,1)位置需要用到(0,1)(1,0)位置的状态值,其他的位置推导同理。
重新回到状态转移方程,dp[i][j]=max(dp[i][j-1],dp[i-1][j])+frame[i-1][j-1]
对于(1,1)点,dp[1][1]应该是它本身的价值,所以max(dp[i][j-1],dp[i-1[j])的值应该要为零。故把dp[i][j-1]=dp[i-1][j]置零。
对于第一行其他的点,他们的上方位置的价值应该是零,因为到不了哪些位置,所以也置零。
对于第一列同理。(这里说的第一行第一列是对于紫色框框来说的)
所以我们可以统一将dp数组置0,即可。
所以初始化是将dp数组全部置零。
填表顺序
从左到右,从上到下
返回值
返回最后一个值即可,即:dp[row][col]
代码实现
int jewelleryValue(int** frame, int frameSize, int* frameColSize) {int row=frameSize;int col=frameColSize[0];int dp[row+1][col+1];for(int i=0;i<=row;i++){memset(dp[i],0,sizeof(dp[i]));}for(int i=1;i<=row;i++){for(int j=1;j<=col;j++){dp[i][j]=fmax(dp[i-1][j],dp[i][j-1])+frame[i-1][j-1];}}return dp[row][col];
}931. 下降路径最小和
题目解析

状态表示
我们可以定义dp[i][j]表示,从开头某一位置出发,到达(i,j)位置时,下降路径的最小和。
状态转移方程
对于(i,j)位置,需要得到,从开头某一位置出发,到达(i,j)位置时,下降路径的最小和。
我们想一想能不能由其他状态推导出(i,j)位置状态的值。
到达(i,j)位置一共有三种情况,要么从(i-1,j-1)位置往右下走一步,要么从(i-1,j)位置往下走一步,要么从(i-1,j+1)位置往左下走一步。
dp[i-1][j-1]表示从开头某一位置出发,到达(i-1,j-1)位置时,下降路径的最小和。
dp[i-1][j]表示从开头某一位置出发,到达(i-1,j)位置时,下降路径的最小和。
dp[i-1][j+1]表示从开头某一位置出发,到达(i-1,j+1)位置时,下降路径的最小和。
所以很容易得到,dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+matrix[i][j];
故,状态转移方程为:
dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+matrix[i][j];
初始化
根据状态转移方程,我们需要推导(i,j)位置的值,需要运用(i-1,j-1),(i-1,j),(i-1,j+1)的值。
所以我们必须初始化第一行,第一列,和最后一列的数据。
我们发现这样的初始化操作十分的复杂。
我们希望简化这种复杂的操作。
所以我们把这些需要初始化的位置用虚拟节点代替,而原先需要初始化的位置改变为初始化虚拟节点。
我们知道初始化虚拟节点一般都是比较轻松的。
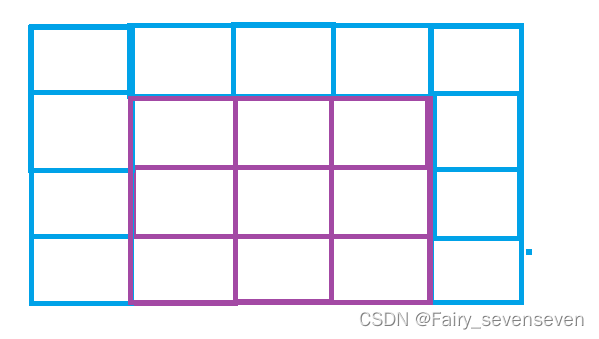
我们选择多添加一行和两列作为虚拟节点。将所有我们需要填写的状态位置都通过状态转移方程推导得到,这样我们就只需要初始化虚拟节点就可以了。
创建虚拟节点有几点注意事项:
第一,虚拟节点的初始化必须保证后续推导过程求值得准确性。
第二,注意下表得映射关系,也就是状态表示和状态转移方程的下标需要偏移。
接下来我们通过实际的含义,初始化虚拟节点里面的值。
关注我们需要填写的状态的第一行,也就是紫色框框圈住的第一行。
对于这些数据,我们需要用到蓝色第一行的数据,由状态转移方程,dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+matrix[i-1][j-1];,实际上紫色的一行填写的数据一个就是matrix[i-1][j-1]
所以min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])值一个要为零。
所以蓝色第一行我们初始化为零。
关注我们需要填写的状态的第一列,也就是紫色第一列。
除第一个元素我们考虑过,其他的元素都需要用到蓝色第一列的数据。
dp[i][j]=min(dp[i-1][j-1],dp[i-1][j],dp[i-1][j+1])+matrix[i-1][j-1];
在三者去最小的时候,我们不能取到dp[i-1][j-1]位置的值,所以这些位置应该初始化无穷大。
最后一列的初始化同理。
所以初始化操作为:
蓝色第一行全部初始化为零,第一列和最后一列初始化为无穷大。
填表顺序
从左往右,从上往下
返回值
我们需要得到从最上面开始出发,到达最下面的路径最小和,所以我们需要访问最后一行的元素,找到他们的最小值返回即可。
代码实现
int minFallingPathSum(int** matrix, int matrixSize, int* matrixColSize) {int row=matrixSize;int col=matrixColSize[0];int dp[row+1][col+2];for(int i=0;i<=row;i++){memset(dp[i],0,sizeof(dp[i]));}for(int i=1;i<=row;i++){dp[i][0]=0x3f3f3f;dp[i][col+1]=0x3f3f3f;}for(int i=1;i<=row;i++){for(int j=1;j<=col;j++){dp[i][j]=fmin(dp[i-1][j-1],fmin(dp[i-1][j],dp[i-1][j+1]))+matrix[i-1][j-1];}}int ret=INT_MAX;for(int i=1;i<=col;i++){ret=fmin(ret,dp[row][i]);}return ret;
}我们首先把所有的数据初始化为零。然后再初始化第一列和最后一列的元素,初始化为无穷大。
这里我们可以用INT_MAX表示,也可以用0x3f3f3f3f表示。
0x3f3f3f3f是一个很有用的数值,它是满足以下两个条件的“最大整数”。
1、整数的两倍不超过 0x7f7f7f7f,即int能表示的最大正整数。
2、整数的每8位(每个字节)都是相同的。
我们在程序设计中经常需要使用 memset(a, val, sizeof a) 初始化一个数组a,该语句把数值 val(0x00~0xFF)填充到数组a 的每个字节上,所以用memset只能赋值出“每8位都相同”的 int。
当需要把一个数组中的数值初始化成正无穷时,为了避免加法算术上溢出或者繁琐的判断,我们经常用 memset(a, 0x3f, sizeof(a)) 给数组赋 0x3f3f3f3f的值来代替。
0x3f3f3f3f通常用于表示无穷大。
64. 最小路径和

题目解析
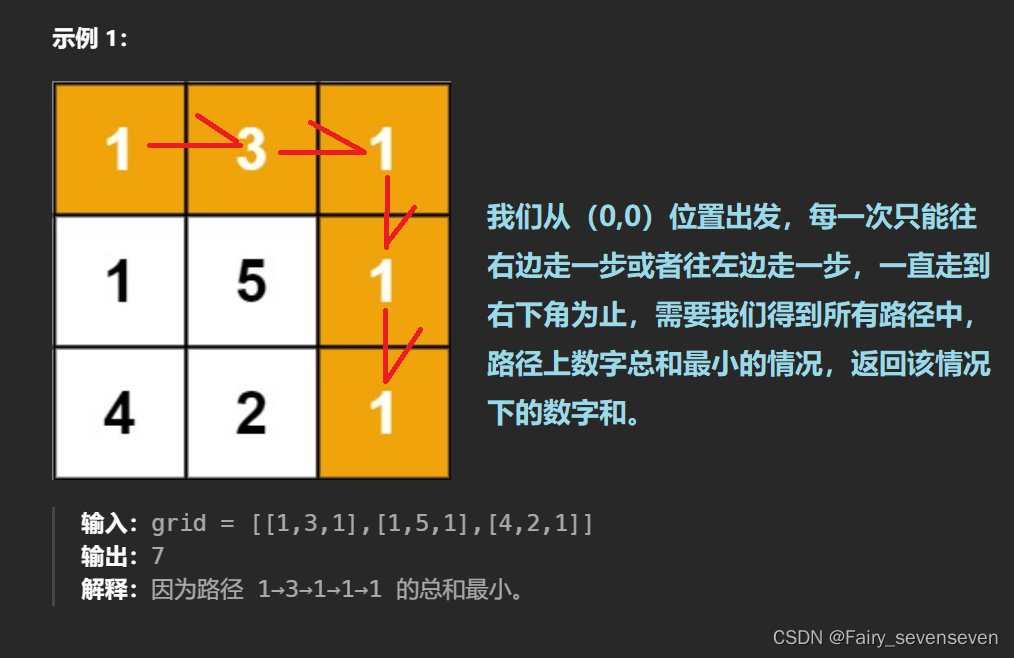
状态表示
我们可以定义,dp[i][j]表示,从(0,0)位置出发,到达(i,j)位置的所有情况下最小路径和。
状态转移方程
我们想一想,(i,j)位置的状态能不能由其他的位置推导得出来?
如果我们要到达(i,j)位置,要么从(i,j-1)位置向右走一步,要么从(i-1,j)位置向下走一步,dp[i][j]表示,从(0,0)位置出发,到达(i,j)位置的所有情况下最小路径和。
dp[i-1][j]表示,从(0,0)位置出发,到达(i-1,j)位置的所有情况下最小路径和。
dp[i][j-1]表示,从(0,0)位置出发,到达(i,j-1)位置的所有情况下最小路径和。
很容易可以得到,dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]
故,状态转移方程为:
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]
初始化
根据状态转移方程,我们知道,如果要推导出(i,j)位置的状态值,我们需要用到(i,j-1)和(i-1,j)位置的状态值,所以我们需要初始化第一列和第一行的所有数据的值。当然我们也可以添加虚拟节点,使得所有状态值都可以用状态转移方程推导得出,将所有的状态进行统一化,这样我们就不用初始化第一行和第一列的状态,转而初始化虚拟节点的状态就可以了,而初始化虚拟节点的值是比较容易实现的。因为我们要使得原先第一行和第一列的数据可以有前驱使得可以利用状态转移方程推导得出,所以我们需要添加一列和一行。
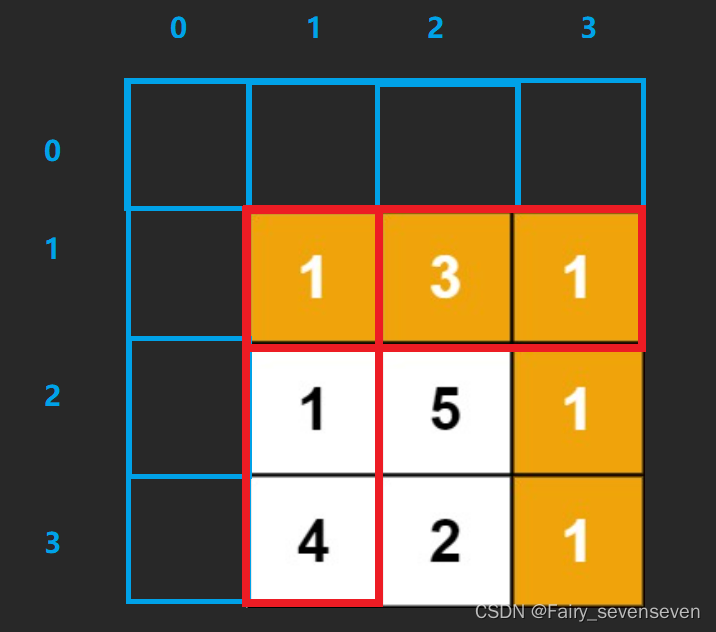
添加虚拟节点有几点注意事项:
第一,初始化虚拟节点的值,必须保证正确性,不能使得后续状态的推导出错。
第二,注意dp数组下标和原数组下标的映射关系,也就是状态表示和状态转移方程的下标映射关系。
我们目光回到红色框框住的一行和一列。
对于这些数据我们需要访问虚拟节点的值,推导出自己的状态值,状态转移方程是,
dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]
对于(1,1)位置的状态,实际上他的值应该是他自己,根据状态转移方程,min(dp[0][1],dp[1][0])的值应该为0
对于行来说,除去第一个数据,其他的状态推导中不能取虚拟节点的值,所以上面虚拟节点的值应该为正无穷。
对于列来说,同理,左边虚拟节点的值也应该为正无穷。
所以我们可以把所有数据都初始化正无穷,dp[0][1]和dp[1][0]位置选一个置0即可。
填表顺序
从左往右,从上往下
返回值
返回dp[row][col]最后一个数据的值。
代码实现
int minPathSum(int** grid, int gridSize, int* gridColSize) {int row=gridSize;int col=gridColSize[0];int dp[row+1][col+1];for(int i=0;i<=row;i++){memset(dp[i],0x3f3f3f3f,sizeof(dp[i]));}dp[0][1]=0;for(int i=1;i<=row;i++){for(int j=1;j<=col;j++){dp[i][j]=fmin(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];}}return dp[row][col];
}0x3f3f3f3f是一个很有用的数值,它是满足以下两个条件的“最大整数”。
1、整数的两倍不超过 0x7f7f7f7f,即int能表示的最大正整数。
2、整数的每8位(每个字节)都是相同的。
我们在程序设计中经常需要使用 memset(a, val, sizeof a) 初始化一个数组a,该语句把数值 val(0x00~0xFF)填充到数组a 的每个字节上,所以用memset只能赋值出“每8位都相同”的 int。
当需要把一个数组中的数值初始化成正无穷时,为了避免加法算术上溢出或者繁琐的判断,我们经常用 memset(a, 0x3f, sizeof(a)) 给数组赋 0x3f3f3f3f的值来代替。
0x3f3f3f3f通常用于表示无穷大。
结尾
今天我们学习了动态规划的思想,动态规划思想和数学归纳法思想有一些类似,动态规划在模拟数学归纳法的过程,已知一个最简单的基础解,通过得到前项与后项的推导关系,由这个最简单的基础解,我们可以一步一步推导出我们希望得到的那个解,把我们得到的解依次存放在dp数组中,dp数组中对应的状态,就像是数列里面的每一项。最后感谢您阅读我的文章,对于动态规划系列,我会一直更新,如果您觉得内容有帮助,可以点赞加关注,以快速阅读最新文章。
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
相关文章:

【三】【C语言\动态规划】珠宝的最高价值、下降路径最小和、最小路径和,三道题目深度解析
动态规划 动态规划就像是解决问题的一种策略,它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题,并将每个小问题的解保存起来。这样,当我们需要解决原始问题的时候,我们就可以直接利…...
爬虫工作量由小到大的思维转变---<第二十八章 Scrapy中间件说明书>
爬虫工作量由小到大的思维转变---<第二十六章 Scrapy通一通中间件的问题>-CSDN博客 前言: (书接上面链接)自定义中间件玩不明白? 好吧,写个翻译的文档点笔记,让中间件更通俗一点!!! 正文: 全局图: 爬虫中间件--->翻译笔记: from scrapy import s…...
从Maven初级到高级
一.Maven简介 Maven 是 Apache 软件基金会组织维护的一款专门为 Java 项目提供构建和依赖管理支持的工具。 一个 Maven 工程有约定的目录结构,约定的目录结构对于 Maven 实现自动化构建而言是必不可少的一环,就拿自动编译来说,Maven 必须 能…...

orangepi--开发板配置网络SSH登录
常用指令: ifconfig-------------------------------------查看网络地址 sudo passwd orangepi-------------------------改密码 nmcli dev wifi-------------------------------查看wifi nmcli dev wifi connect xx password xx--------连接网络 ip addr show wla…...

简单通讯录管理系统第4关:简单通讯录管理系统之修改通讯录用户信息
任务描述 本关任务:实现修改通讯录用户电话号码的功能。 编程要求 仔细阅读右侧编辑区内给出的代码框架及注释,在 Begin-End 中实现通讯录管理系统中修改用户信息的功能,具体要求如下: 在 PhoneManage.java 类定义一个 changeP…...

macOS编译ckb-next
macOS x86 成功,下一步,测试:m1、m2、m3 。 1、Homebrew # 三选一 /usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)" # /bin/bash -c "$(curl -fsSL https://raw.gith…...
漏刻有时数据可视化Echarts组件开发(46)散点图颜色判断
series组件 series: [{name: Top 5,type: scatter,coordinateSystem: bmap,data: convertData(data.sort(function (a, b) {return b.value - a.value;}).slice(0, 6)),symbolSize: 20,encode: {value: 2},showEffectOn: render,rippleEffect: {brushType: stroke},label: {fo…...

智能优化算法应用:基于驾驶训练算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于驾驶训练算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于驾驶训练算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.驾驶训练算法4.实验参数设定5.算法结果6.…...
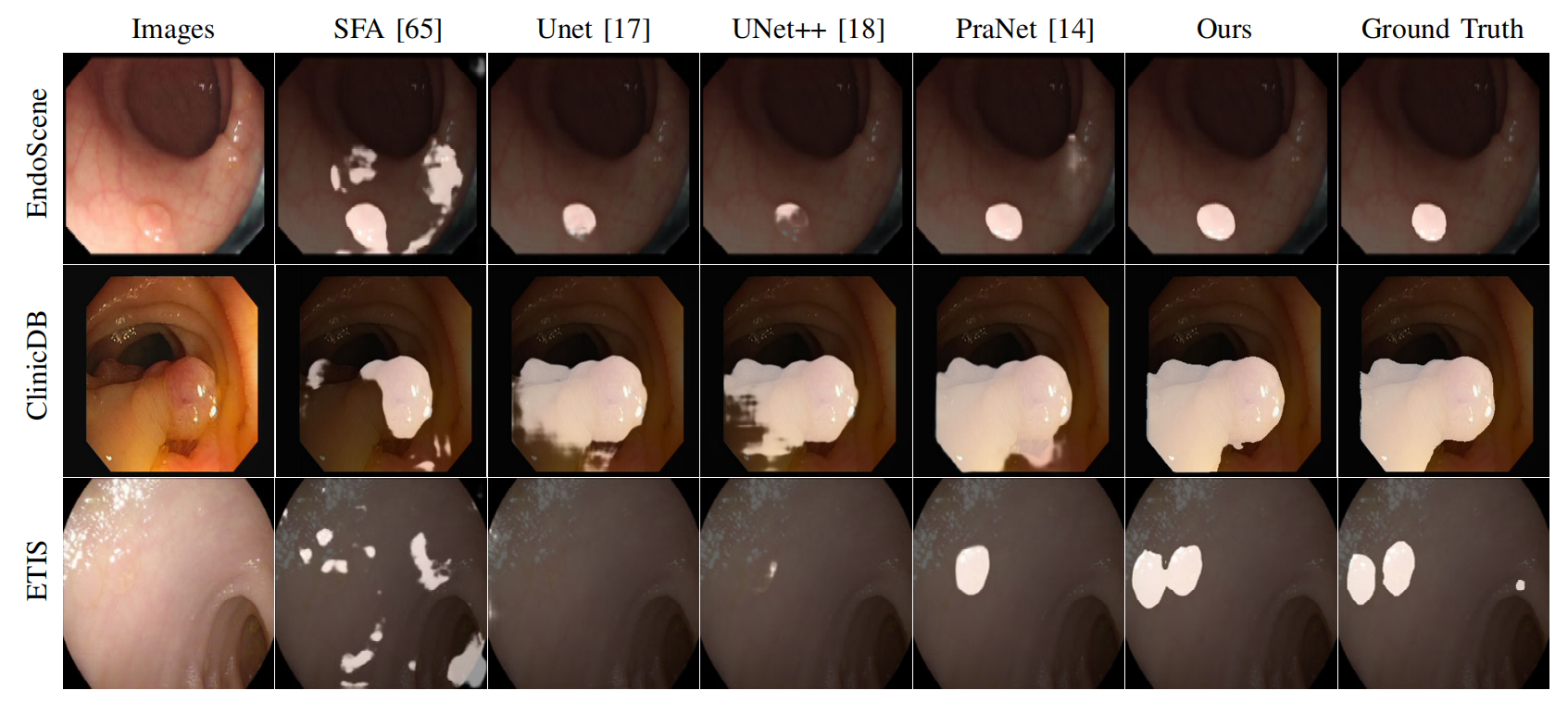
【论文阅读】MCANet: Medical Image Segmentation with Multi-Scale Cross-Axis Attention
文章目录 摘要创新点总结实现效果总结 摘要 链接:https://arxiv.org/abs/2312.08866 医学图像分割是医学图像处理和计算机视觉领域的关键挑战之一。由于病变区域或器官的大小和形状各异,有效地捕捉多尺度信息和建立像素间的长距离依赖性至关重要。本文提…...

机器视觉实战应用:手势、人脸、动作以及手势鼠标构建(一)
CV实战应用手势、人脸、动作以及手势鼠标构建(一)总起 核心思想 手势识别是一种常见的计算机视觉应用,它可以通过摄像头或者预先录制的视频图像来追踪和识别人类手势。手势识别的应用非常广泛,例如在游戏、虚拟现实、人机交互等…...

python作业题百度网盘,python作业答案怎么查
大家好,小编来为大家解答以下问题,python作业题百度网盘,python作业答案怎么查,今天让我们一起来看看吧! 1 以下代码的输出结果为: alist [1, 2, 3, 4] print(alist.reverse()) print(alist) A.[4, 3, 2, …...
centos7.9中离线安装nginx开启ssl,arm架构
一、首先需要去国内相关镜像库下载相关依赖rpm: http://mirrors.bfsu.edu.cn/centos-altarch/7.9.2009/os/aarch64/ http://mirror.nju.edu.cn/centos-altarch/7.9.2009/os/aarch64/ http://mirrors.tuna.tsinghua.edu.cn/centos-altarch/7.9.2009/os/aarch64/ htt…...

LENOVO联想笔记本小新Pro 14 IRH8 2023款(83AL)电脑原装出厂Win11系统恢复预装OEM系统
链接:https://pan.baidu.com/s/1M1iSFahokiIHF3CppNpL4w?pwdzr8y 提取码:zr8y 联想原厂系统自带所有驱动、出厂主题壁纸、Office办公软件、联想电脑管家等自带的预装软件程序 所需要工具:16G或以上的U盘 文件格式:ISO 文件…...

blender使用faceit绑定自己的表情动作
blender使用faceit绑定自己的表情控制模型 faceit是个神器,来记录一下如何让表情动起来保持相对位置头部分离,方便后续绑定faceitfaceit的注册rig生成地标Animate可以修正表情烘培之前记得保存使用Faceit的整个流程 faceit是个神器,来记录一下…...

有关List的线程安全、高效读取:不变模式下的CopyOnWriteArrayList类、数据共享通道:BlockingQueue
有关List的线程安全 队列、链表之类的数据结构也是极常用的,几乎所有的应用程序都会与之相关。在java中, ArrayList和Vector都使用数组作为其内部实现。两者最大的不同在与Vector是线程安全的。 而ArrayList不是。此外LinkedList使用链表的数据结构实现…...

OCC服务器和BCC服务器中文件同步
OCC服务器到BCC服务器文件正向同步 需求:编写shell脚本,使用rsync命令来同步目录,把全部需要同步的目录放在配置文件中,设置定时任务自动同步 服务器IP: 服务器类型IP地址OCC服务器192.168.1.188BCC服务器192.168.1…...
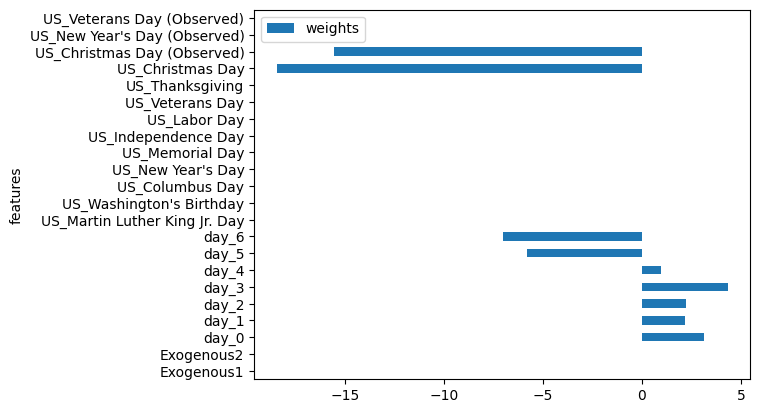
工具系列:TimeGPT_(2)使用外生变量时间序列预测
文章目录 TimeGPT使用外生变量时间序列预测导入相关工具包预测欧美国家次日电力价格案例 TimeGPT使用外生变量时间序列预测 外生变量在时间序列预测中非常重要,因为它们提供了可能影响预测的额外信息。这些变量可以包括假日标记、营销支出、天气数据或与你正在预测…...
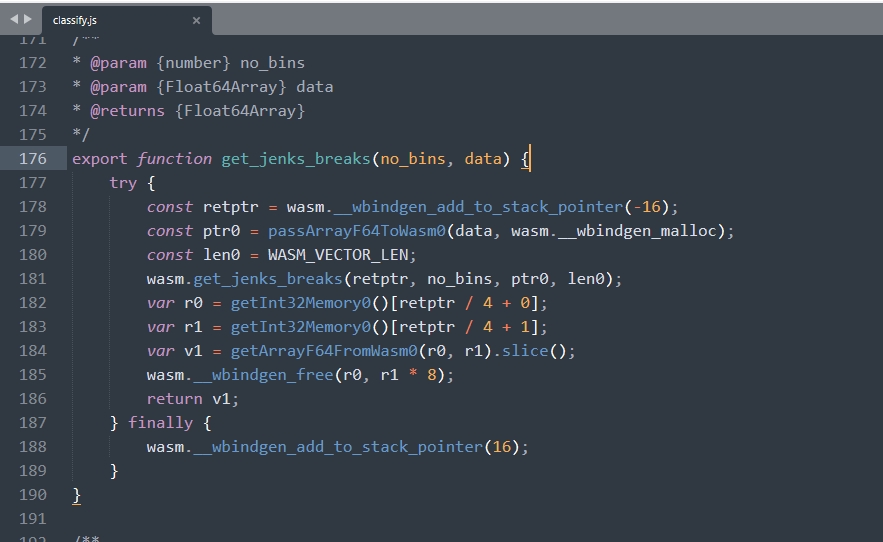
应用于前端的自然断点法:wasm应用示例
某月某日,虾神本虾接到了这样一个需求,前端获取数据之后,在渲染之前,要对数据进行分类,分类的方法可以选择常用几种,例如等距法、自然断点法、标准差分类法等…… 问:为什么要在前端࿱…...
数组)
web前端javaScript笔记——(6)数组
对象一般分为内建对象,宿主对象,自定义对象。 数组(Array) 数组也是一个对象 它和我们普通对象功能类似,也是用来存储一些值的 不同的是普通对象是使用字符串作为属性名的,而数组时使用数字来作为索引操作元素案引: 从0开始的…...

vue的props
Vue的props是组件之间传递数据的一种方式,可以在组件中定义props并接收外部传递的数据。 在父组件中使用子组件时,可以使用v-bind指令将数据传递给子组件的props。子组件中可以通过props属性接收并使用这些数据。 父组件中: <template&…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
