Dijkstra(迪杰斯特拉)算法总结
知识概览
- Dijkstra算法适用于解决所有边权都是正数的最短路问题。
- Dijkstra算法分为朴素的Dijkstra算法和堆优化版的Dijkstra算法。
- 朴素的Dijkstra算法时间复杂度为
,适用于稠密图。堆优化版的Dijkstra算法时间复杂度为
,适用于稀疏图。
- 稠密图的边数m和
是一个级别的,稀疏图的边数m和点数n是一个级别的。
朴素的Dijkstra算法
例题展示
题目链接
活动 - AcWing系统讲解常用算法与数据结构,给出相应代码模板,并会布置、讲解相应的基础算法题目。![]() https://www.acwing.com/problem/content/description/851/
https://www.acwing.com/problem/content/description/851/
代码
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 510;int n, m;
int g[N][N];
int dist[N];
bool st[N];int dijkstra()
{// dist[1] = 0, dist[i] = 无穷大memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < n - 1; i++){int t = -1;for (int j = 1; j <= n; j++)if (!st[j] && (t == -1 || dist[t] > dist[j]))t = j; // t为不在st为false的距离最近的点st[t] = true;// 用t更新其它点的距离for (int j = 1; j <= n; j++)dist[j] = min(dist[j], dist[t] + g[t][j]);}if (dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}int main()
{scanf("%d%d", &n, &m);memset(g, 0x3f, sizeof g);while (m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);g[a][b] = min(g[a][b], c); // 重边取最小距离}int t = dijkstra();printf("%d\n", t);return 0;
}堆优化版的Dijkstra算法
例题展示
题目链接
活动 - AcWing系统讲解常用算法与数据结构,给出相应代码模板,并会布置、讲解相应的基础算法题目。![]() https://www.acwing.com/problem/content/852/
https://www.acwing.com/problem/content/852/
代码
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>using namespace std;typedef pair<int, int> PII;const int N = 150010;int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}int dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, 1});while (heap.size()){auto t = heap.top();heap.pop();int ver = t.second, distance = t.first;if (st[ver]) continue;st[ver] = true;for (int i = h[ver]; i != -1; i = ne[i]){int j = e[i];if (dist[j] > distance + w[i]){dist[j] = distance + w[i];heap.push({dist[j], j});}}}if (dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}int main()
{scanf("%d%d", &n, &m);memset(h, -1, sizeof h);while (m--){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}int t = dijkstra();printf("%d\n", t);return 0;
}参考资料
- AcWing算法基础课
相关文章:
Dijkstra(迪杰斯特拉)算法总结
知识概览 Dijkstra算法适用于解决所有边权都是正数的最短路问题。Dijkstra算法分为朴素的Dijkstra算法和堆优化版的Dijkstra算法。朴素的Dijkstra算法时间复杂度为,适用于稠密图。堆优化版的Dijkstra算法时间复杂度为,适用于稀疏图。稠密图的边数m和是一…...

设计模式?!
如何解决复杂性 链接:不同的设计模式实例代码(更新中) 分解 人们面对复杂性有一个常见的做法:即分而治之,将大问题分解为多个小问题,将复杂问题分解为多个简单问题。 抽象 更高层次来讲,人们处…...

Pytorch项目,肺癌检测项目之三
成功获取到数据之后,我们需要将数据放到Pytorch里面去处理,我们需要将其转换成Dataset数据集,方便去使用相同的API。要转换成Dataset数据集需要实现两个方法,方法一: 方法二: 运行比较慢的话,…...
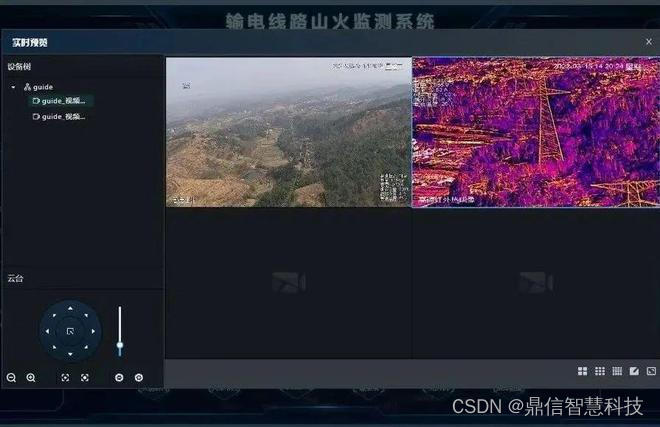
深圳鼎信|输电线路防山火视频监控预警装置:森林火灾来袭,安全不留白!
受线路走廊制约和环保要求影响,输电线路大多建立在高山上,不仅可以减少地面障碍物和人类活动的干扰,还能提高线路的抗灾能力和可靠性。但同时也会面临其它的难题,例如森林火灾预防。今天,深圳鼎信智慧将从不同角度分析…...

【Bash/Shell】知识总结
文章目录 1. 总体认识1.1. Shell概述1.2. 第一个Shell脚本1.3. 注释 2. 变量2.1. 定义变量2.2. 使用变量2.3. 只读变量2.4. 删除变量2.5. 变量类型2.5.1. 字符串变量2.5.2. 整数变量2.5.3. 数组变量2.5.4. 环境变量2.5.5. 特殊变量 3. 输出3.1. echo命令3.2. printf命令 4. 运算…...

单例模式(C++实现)
RAII运用 只能在栈上创建对象 只能在堆上创建的对象 单例模式 设计模式 懒汉模式 解决线程安全 优化 饿汉模式 饿汉和懒汉的区别 线程安全与STL与其他锁...

ElasticSearch 聚合统计
聚合统计 度量聚合:求字段的平均值,最小值,最大值,总和等 桶聚合:将文档分成不同的桶,桶的划分可以根据字段的值,范围,日期间隔 管道聚合:在桶聚合的结果上执行进一步计…...

SpringIOC之MethodBasedEvaluationContext
博主介绍:✌全网粉丝5W+,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战,博主也曾写过优秀论文,查重率极低,在这方面有丰富的经验✌ 博主作品:《Java项目案例》主要基于SpringBoot+MyBatis/MyBatis-plus+…...
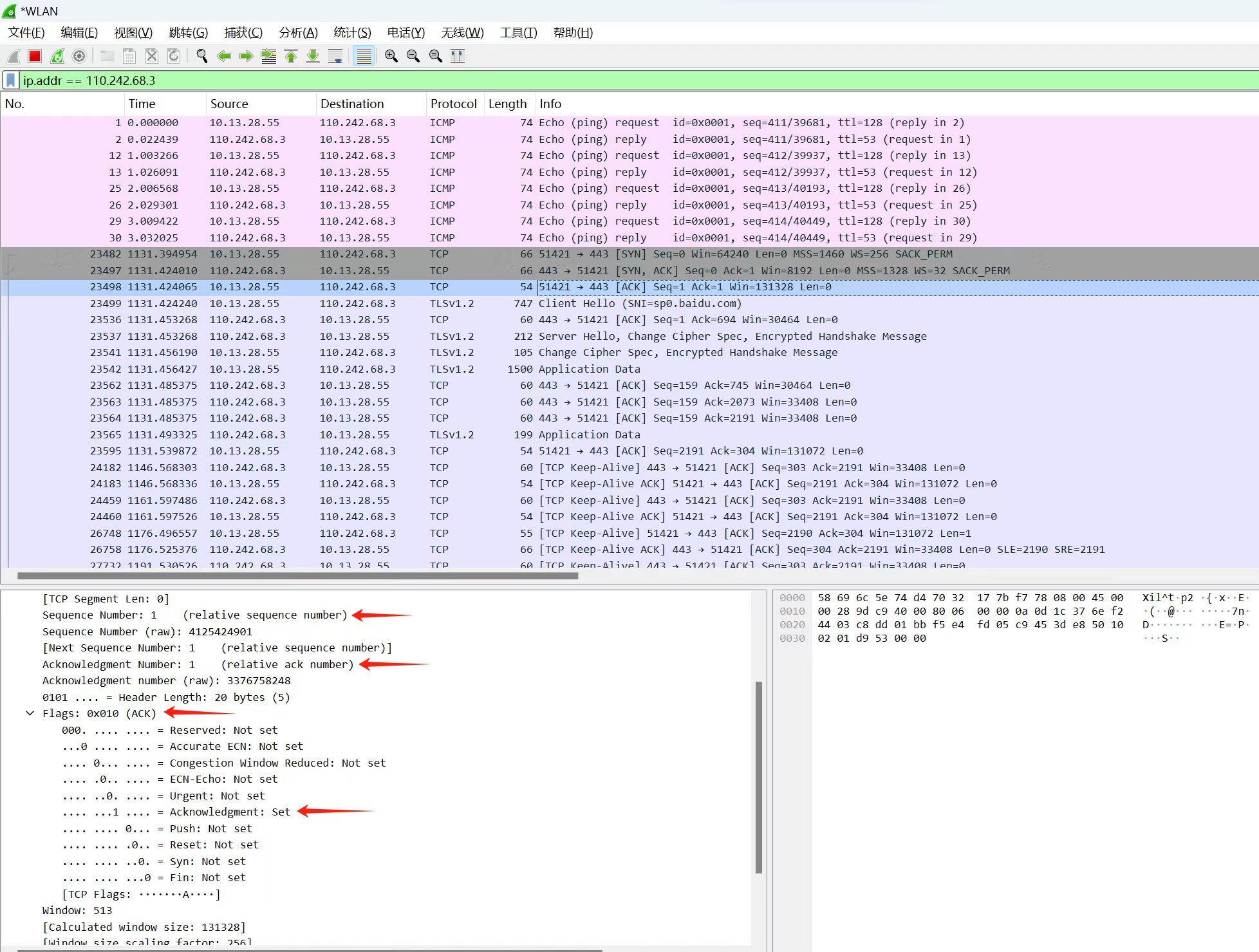
【网络安全 | 网络协议】结合Wireshark讲解TCP三次握手
前言 TCP(传输控制协议)是一种面向连接的、可靠的传输层协议。在建立 TCP 连接时,需要进行三次握手,防止因为网络延迟、拥塞等原因导致的数据丢失或错误传输,确保双方都能够正常通信。 TCP三次握手在Wireshark数据包中…...

钦丰科技(安徽)股份有限公司携卫生级阀门管件盛装亮相2024发酵展
钦丰科技(安徽)股份有限公司携卫生级阀门管件盛装亮相2024济南生物发酵展! 展位号:2号馆A65展位 2024第12届国际生物发酵产品与技术装备展览会(济南)于3月5-7日在山东国际会展中心盛大召开,展会同期将举办30余场高质…...

Python模拟动态星空
前言 今天,我们来用Python做个星空。 一、模拟星空 1,.首先导入所需要的库: from turtle import * from random import random, randint 2.初始画面: screen Screen() width, height 800, 600 screen.setup(width, height) screen.tit…...
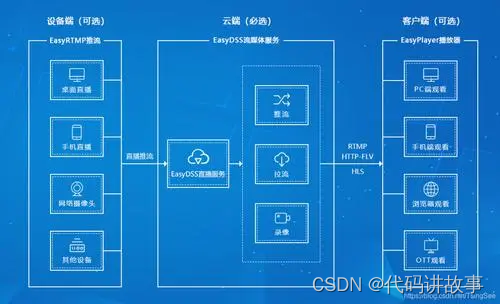
最新技术整理3款开源免费直播推流工具,实现实时视频推流、视频拉流,目标端可以是服务器、云平台、移动设备等(附源码)
最新技术整理3款开源免费直播推流工具,实现实时视频推流、视频拉流,目标端可以是服务器、云平台、移动设备等(附源码)。 什么是推流? 视频推流是指将实时的视频数据从一个源端发送到一个或多个目标端的过程。推流的源…...

shell ——数组
数组中可以存放多个值,Bash Shell只能支持以为数字,初始化时不需要定义数组大小。 数组中元素下标从0开始。 数组的定义 shell数组用括号来表示,元素用空格分割开。 array_name(value1 value2 value3 ...) 给一个简单数组例子 cat firs…...
:包的介绍)
GO语言基础笔记(五):包的介绍
在Go语言中,包(package)是代码组织和重用的基本单位。Go的标准库中包含了许多实用的包,它们提供了从基础数据处理到复杂网络编程等各种功能。下面是一些常用的Go标准库包及其作用的介绍: 目录 1. fmt 2. net/http …...
【Unity6.0+AI】Sentis加载模型识别手写数字案例实现
按照国际惯例,看效果: 素材准备: 自己在PS中绘制黑底白字手写字体,导出jpg,尺寸28*28! 素材设置 基本步骤 准备工作:从 ONNX Model Zoo 下载手写识别 ONNX 模型文件 【下载模型】MNIST 手写数字识别模型 mnist-12.onnx,并将其拖入项目窗口的 Assets 文件夹。 【下载模…...
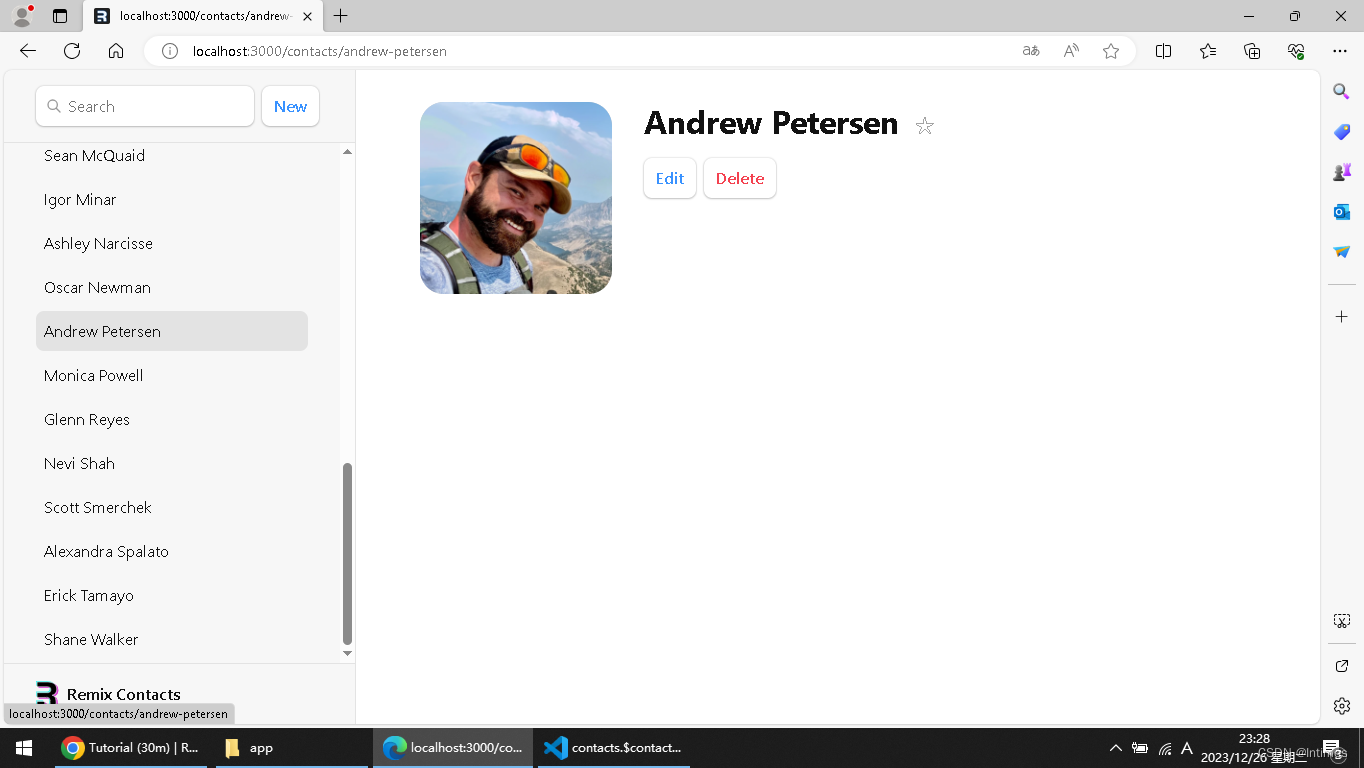
VScode跑通Remix.js官方的contact程序开发过程
目录 1 引言 2 安装并跑起来 3 设置根路由 4 用links来添加风格资源 5 联系人路由的UI 6 添加联系人的UI组件 7 嵌套路由和出口 8 类型推理 9 Loader里的URL参数 10 验证参数并抛出响应 书接上回,我们已经跑通了remix的quick start项目,接下…...
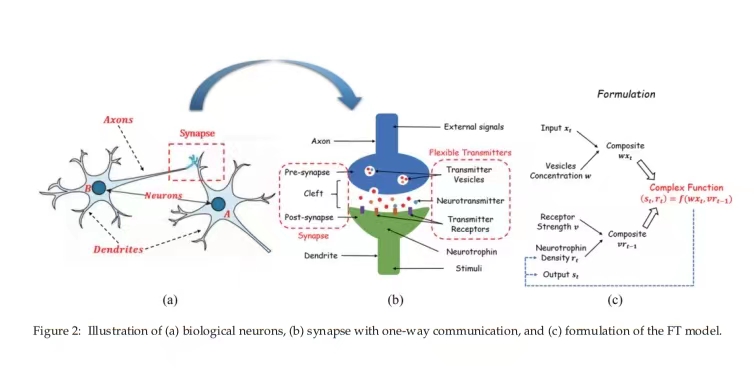
讲座思考 | 周志华教授:新型机器学习神经元模型的探索
12月22日,有幸听了南京大学周志华教授题为“新型机器学习神经元模型的探索”的讲座。现场热闹非凡,大家像追星一样拿着“西瓜书”找周教授签名。周教授讲得依旧循循善诱,由浅入深,听得我很入迷,故作此记。 周教授首先就…...
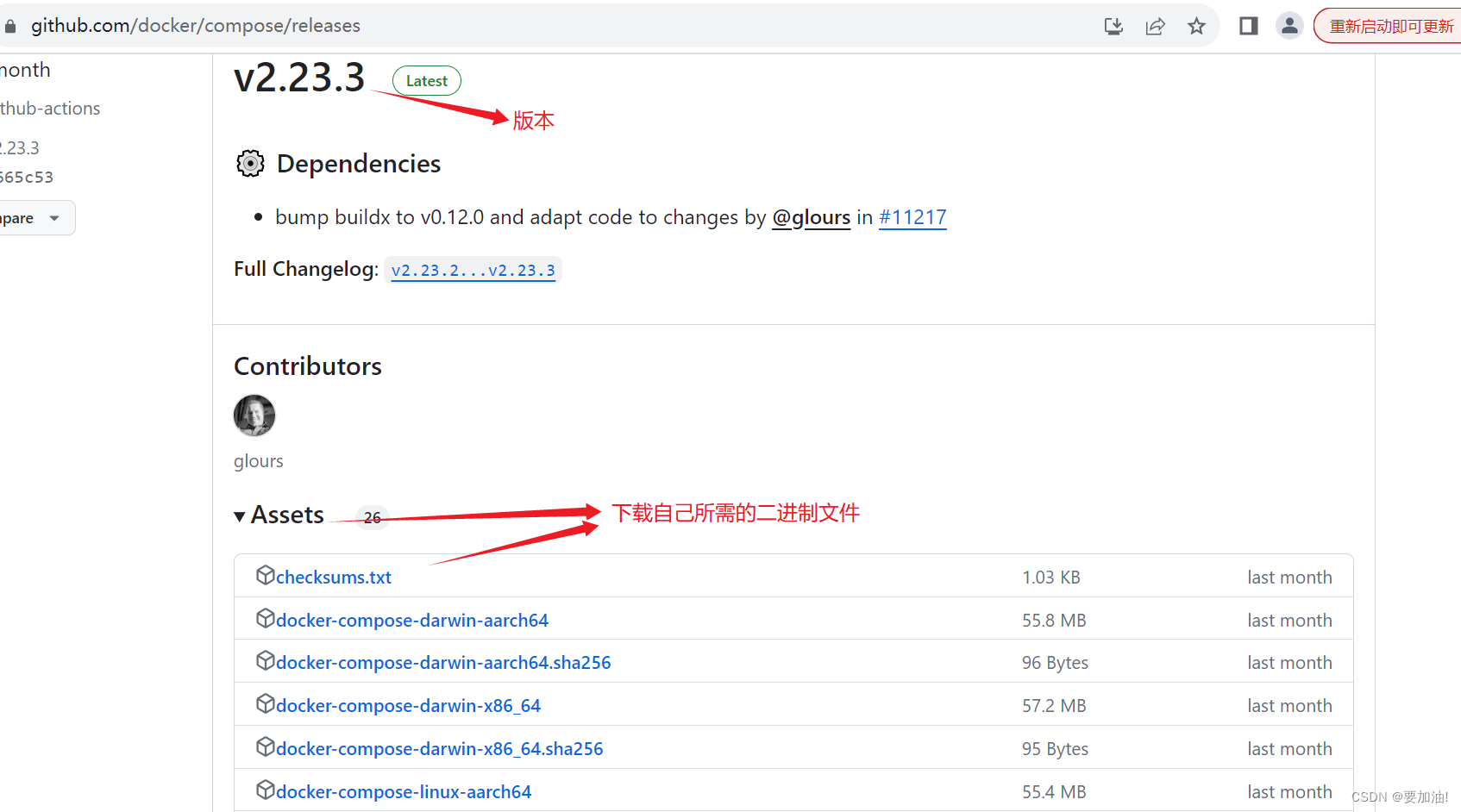
docker构建镜像及项目部署
文章目录 练习资料下载一、docker基础1. 基本概念2. docker常见命令3. 命令别名4. 数据卷 二、docker自定义镜像1. 了解镜像结构2. 了解Dockerfile3. 构建Dockerfile文件,完成自定义镜像 三、网络1. docker常见网络命令2. docker自带虚拟网络3. 自定义网络 四、dock…...

ARM串口通信编程实验
完成:从终端输入选项,完成点灯关灯,打开风扇关闭风扇等操作 #include "gpio.h" int main() {char a;//char buf[128];uart4_config();gpio_config();while(1){//接收一个字符数据a getchar();//发送接收的字符putchar(a);switch(…...
)
MyBatis的延迟加载(懒加载)
MyBatis 中的延迟加载是指在需要时才加载对象的某些属性或关联对象,而不是在初始查询时就加载所有数据。这对于性能优化和减少不必要的数据库查询非常有用。 1. 基于配置文件的延迟加载 在 MyBatis 的 XML 映射文件中,你可以使用 lazyLoadingEnabled 和…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
