2023.12.28每日一题
LeetCode每日一题
2735.收集巧克力
2735. 收集巧克力 - 力扣(LeetCode)
介绍
看题目看不懂,在评论区看到一个大哥解释,瞬间明白了。
一张桌子上有n件商品围成一圈,每件都有一个价签,它们构成数组nums。除了按照价签上的价格买东西之外,你还可以花x块钱把桌子转一下,把每件商品都对应到下一个价签,问把每种商品买一遍最少花多少钱
给你一个长度为 n 、下标从 0 开始的整数数组 nums ,表示收集不同巧克力的成本。每个巧克力都对应一个不同的类型,最初,位于下标 i 的巧克力就对应第 i 个类型。
在一步操作中,你可以用成本 x 执行下述行为:
- 同时修改所有巧克力的类型,将巧克力的类型
ith修改为类型((i + 1) mod n)th。
假设你可以执行任意次操作,请返回收集所有类型巧克力所需的最小成本。
示例 1:
输入:nums = [20,1,15], x = 5
输出:13
解释:最开始,巧克力的类型分别是 [0,1,2] 。我们可以用成本 1 购买第 1 个类型的巧克力。
接着,我们用成本 5 执行一次操作,巧克力的类型变更为 [1,2,0] 。我们可以用成本 1 购买第 2 个类型的巧克力。
然后,我们用成本 5 执行一次操作,巧克力的类型变更为 [2,0,1] 。我们可以用成本 1 购买第 0 个类型的巧克力。
因此,收集所有类型的巧克力需要的总成本是 (1 + 5 + 1 + 5 + 1) = 13 。可以证明这是一种最优方案。
示例 2:
输入:nums = [1,2,3], x = 4
输出:6
解释:我们将会按最初的成本收集全部三个类型的巧克力,而不需执行任何操作。因此,收集所有类型的巧克力需要的总成本是 1 + 2 + 3 = 6 。
提示:
1 <= nums.length <= 10001 <= nums[i] <= 1091 <= x <= 109
思路
LeetCode看的思路,自己没啥思路,还是说自己算法太垃圾,还需多练
nums数组表示购买对应索引类型的巧克力所需要的代价,可以通过每次以代价x来改变(平移)nums数组的分布。
由于nums数组的长度为n,那么进行n次平移操作之后,进入循环。因此有意义的平移操作最多为n-1次。
那么可以使用一个数组costNums来记录每个类型的巧克力,在{0,1,2, …, n-1}次操作过程中购买所需的最小值。在k次操作完成后,将costNums累加并加上k*x,得到操作k次完成购买所需的总代价。
最后,在{0,1,2,…,n-1}次操作中,选择具有最小代价的那次操作。
代码
C++
class Solution {
public:long long minCost(vector<int>& nums, int x) {int n = nums.size();vector<int> costNums(nums); // 初始操作 0 次的成本long long totalCost = accumulate(costNums.begin(), costNums.end(), 0LL); // 初始总成本// enumerate 0 to n-1 times operationfor (int k=1; k<n; k++){// 根据当前操作更新 costNums 数组for (int i=0; i<n; i++) {costNums[i] = min(costNums[i], nums[(i+k)%n]);}// 计算当前操作的总成本并与之前的总成本进行比较,保留最小的totalCost = min(totalCost, accumulate(costNums.begin(), costNums.end(), 0LL) + static_cast<long long>(k)*x);}return totalCost;}
};
Java
class Solution {public long minCost(int[] nums, int x) {int n = nums.length;int[] costNums = Arrays.copyOf(nums, n); // 初始操作 0 次的成本long totalCost = Arrays.stream(costNums).asLongStream().sum(); // 初始总成本for (int k = 1; k < n; k++) {// 根据当前操作更新 costNums 数组for (int i = 0; i < n; i++) {costNums[i] = Math.min(costNums[i], nums[(i + k) % n]);}// 计算当前操作的总成本long currentCost = Arrays.stream(costNums).asLongStream().sum() + (long) k * x;// 如果当前成本更小,更新总成本totalCost = Math.min(totalCost, currentCost);}return totalCost;}
}
相关文章:

2023.12.28每日一题
LeetCode每日一题 2735.收集巧克力 2735. 收集巧克力 - 力扣(LeetCode) 介绍 看题目看不懂,在评论区看到一个大哥解释,瞬间明白了。 一张桌子上有n件商品围成一圈,每件都有一个价签,它们构成数组nums。…...
231227-9步在RHEL8.8配置本地yum源仓库
Seciton 1:参考视频 RHEL8配置本地yum源仓库-安徽迪浮_哔哩哔哩_bilibili Seciton 2:具体操作 🎯 第1步:查看光驱文件/dev/sr0是否已经挂载?此处已挂在 [lgklocalhost ~]$ df -h 🎯 第1步:查看…...
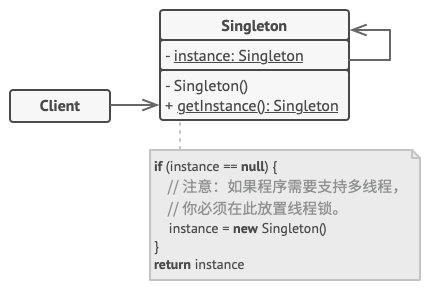
5. 创建型模式 - 单例模式
亦称: 单件模式、Singleton 意图 单例模式是一种创建型设计模式, 让你能够保证一个类只有一个实例, 并提供一个访问该实例的全局节点。 问题 单例模式同时解决了两个问题, 所以违反了单一职责原则: 保证一个类只有一…...
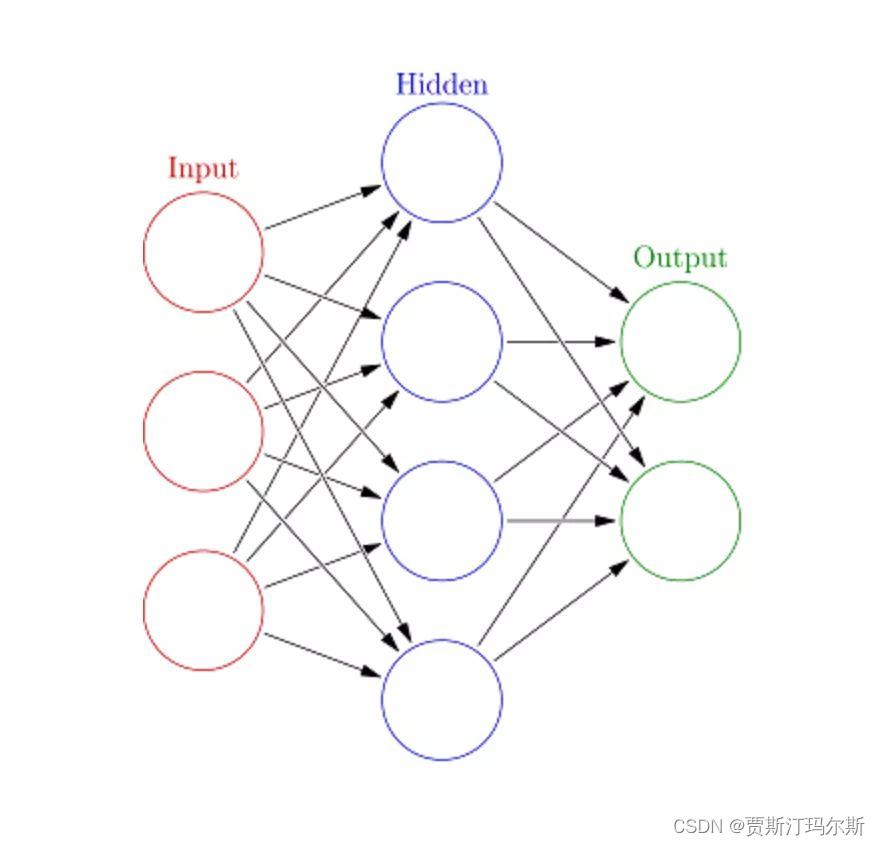
机器学习之人工神经网络(Artificial Neural Networks,ANN)
人工神经网络(Artificial Neural Networks,ANN)是机器学习中的一种模型,灵感来源于人脑的神经网络结构。它由神经元(或称为节点)构成的层级结构组成,每个神经元接收输入并生成输出,这些输入和输出通过权重进行连接。 人工神经网络(ANN)是一种模仿生物神经系统构建的…...
详细介绍)
GetLastError()详细介绍
GetLastError() 是 Windows 操作系统提供的一个函数,用于获取调用线程最近一次发生的错误码。这个函数的定义如下: DWORD GetLastError(void); 调用 GetLastError() 函数可以帮助开发人员在发生错误时获取错误的详细信息,从而进行适当的错…...
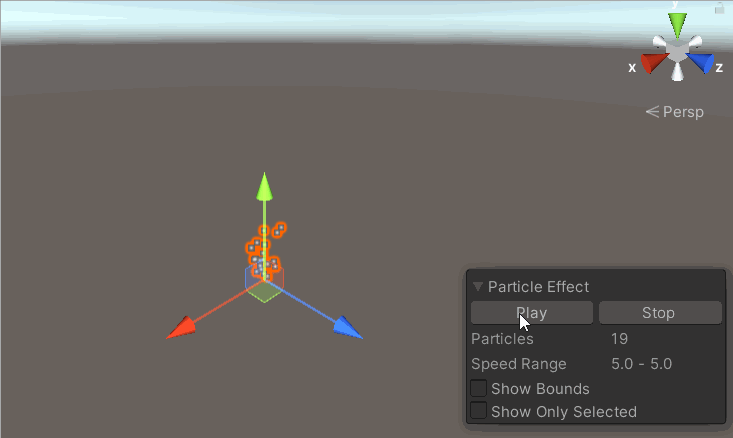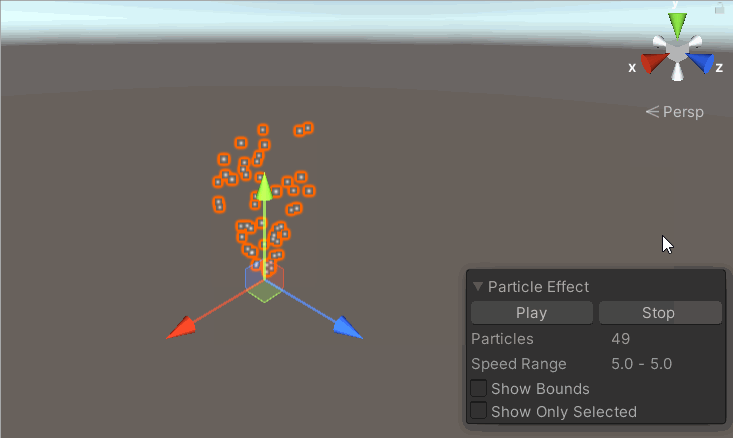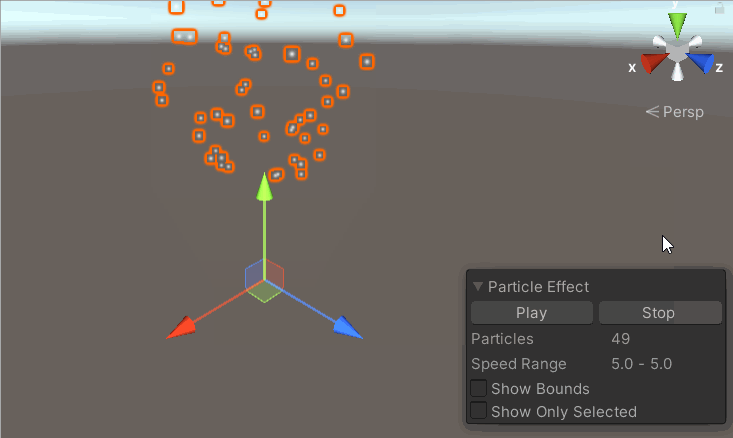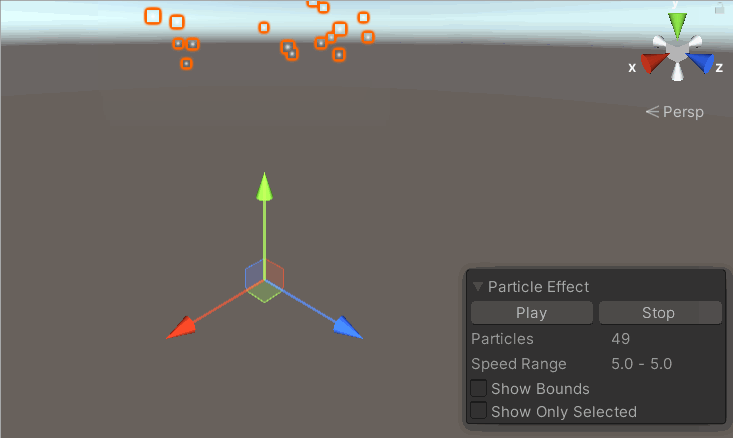
【unity3D-粒子系统】粒子系统主模块-Particle System篇
💗 未来的游戏开发程序媛,现在的努力学习菜鸡 💦本专栏是我关于游戏开发的学习笔记 🈶本篇是unity的粒子系统主模块-Particle System 基础知识 Particle System 介绍:粒子系统的主模块,是必需的模块&#x…...
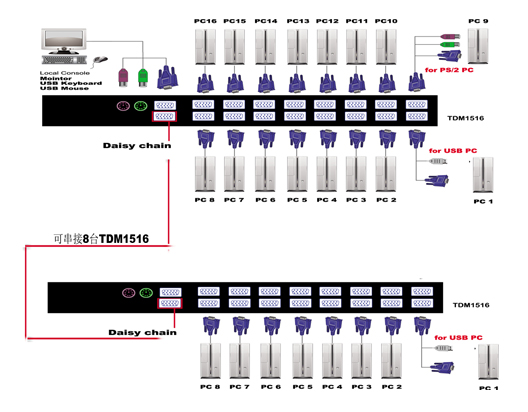
Windows搭建FTP服务器教学以及计算机端口介绍
目录 一. FTP服务器介绍 FTP服务器是什么意思? 二.Windows Service 2012 搭建FTP服务器 1.开启防火墙 2.创建组 编辑3.创建用户 4.用户绑定组 5.安装ftp服务器 编辑6.配置ftp服务器 7.配置ftp文件夹的权限 8.连接测试 三.计算机端口介绍 什么是网络…...
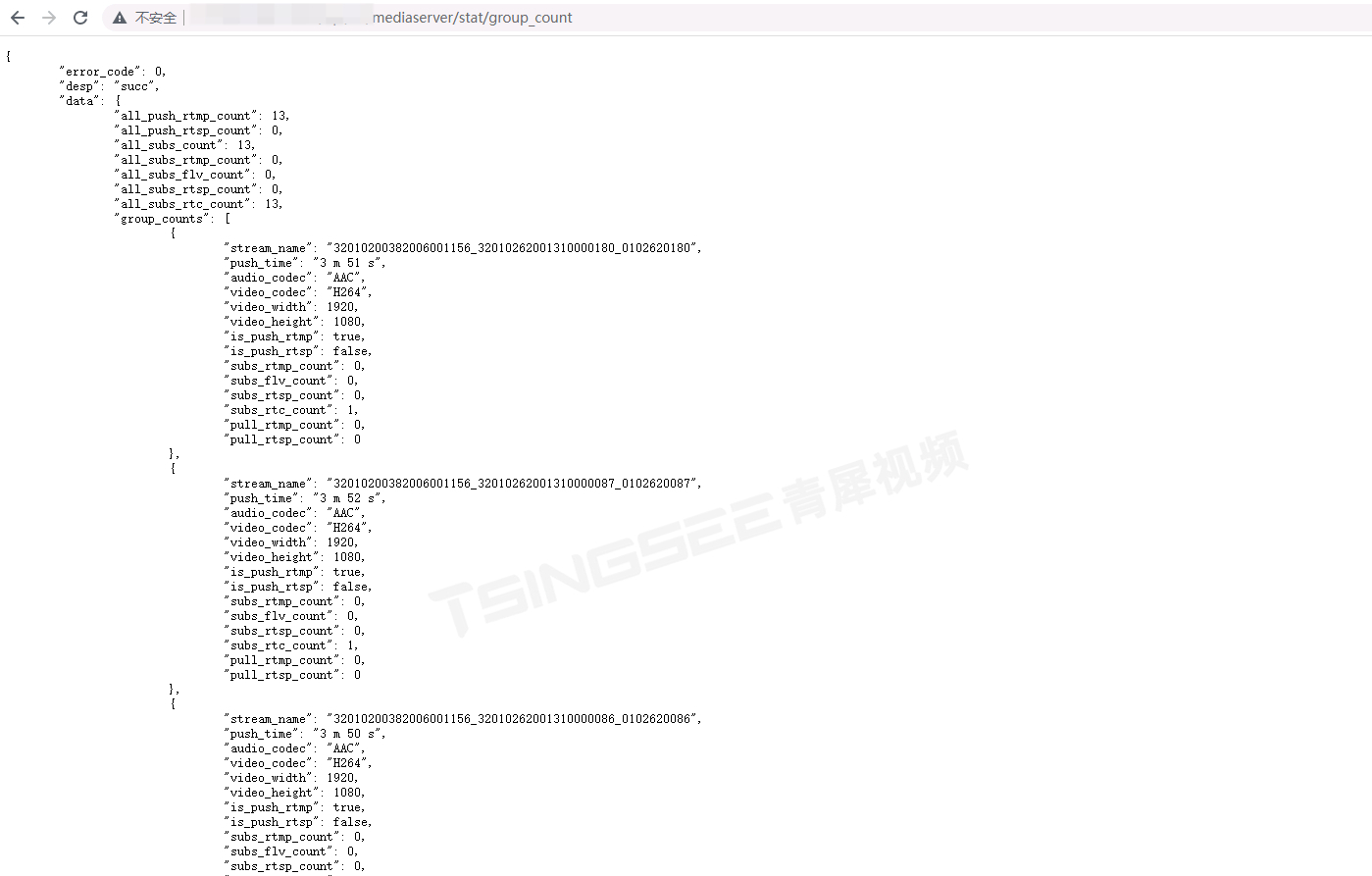
安防视频监控系统EasyCVR实现H.265视频在3秒内起播的注意事项
可视化云监控平台/安防视频监控系统EasyCVR视频综合管理平台,采用了开放式的网络结构,可以提供实时远程视频监控、视频录像、录像回放与存储、告警、语音对讲、云台控制、平台级联、磁盘阵列存储、视频集中存储、云存储等丰富的视频能力,同时…...
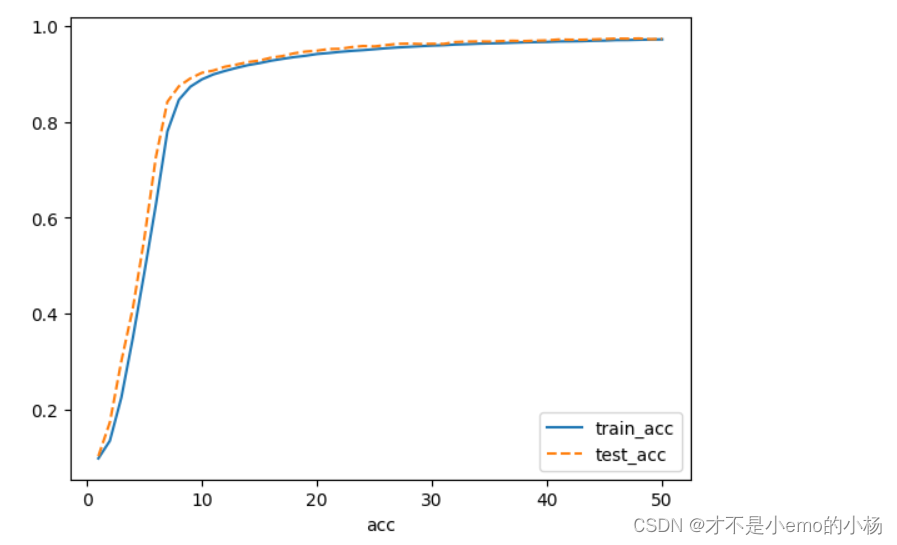
CNN实现对手写字体的迭代
导入库 import torchvision import torch from torchvision.transforms import ToTensor from torch import nn import matplotlib.pyplot as plt 导入手写字体数据 train_dstorchvision.datasets.MNIST(data/,trainTrue,transformToTensor(),downloadTrue) test_dstorchvis…...
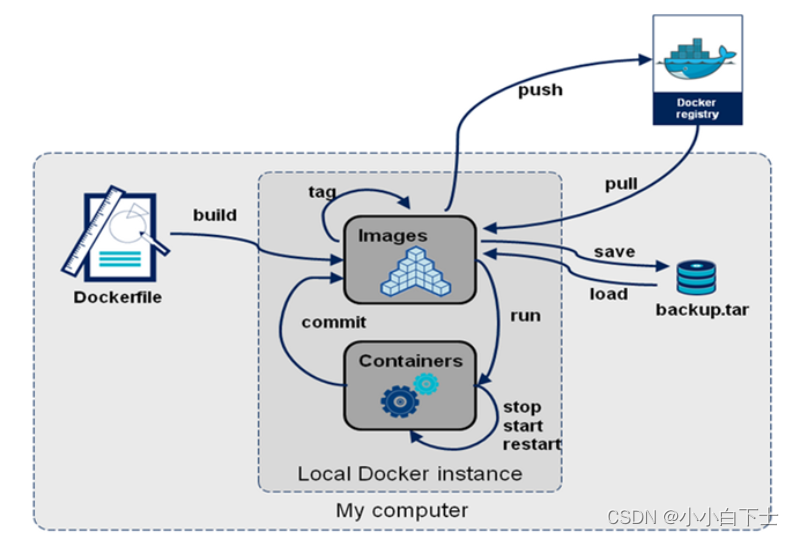
docker学习笔记01-安装docker
1.Docker的概述 用Go语言实现的开源应用项目(container);克服操作系统的笨重;快速部署;只隔离应用程序的运行时环境但容器之间可以共享同一个操作系统;Docker通过隔离机制,每个容器间是互相隔离…...

【《设计模式之美》】如何取舍继承与组合
文章目录 什么情况下不推荐使用继承?组合相比继承有哪些优势?使用组合、继承的时机 本文主要想了解: 为什么组合优于继承,多用组合少用继承。如何使用组合来替代继承哪些情况适用继承、组合。有哪些设计模式使用到了继承、组合。 …...

一步到位:用Python实现PC屏幕截图并自动发送邮件,实现屏幕监控
在当前的数字化世界中,自动化已经成为我们日常生活和工作中的关键部分。它不仅提高了效率,还节省了大量的时间和精力。在这篇文章中,我们将探讨如何使用Python来实现一个特定的自动化任务 - PC屏幕截图自动发送到指定的邮箱。 这个任务可能看…...
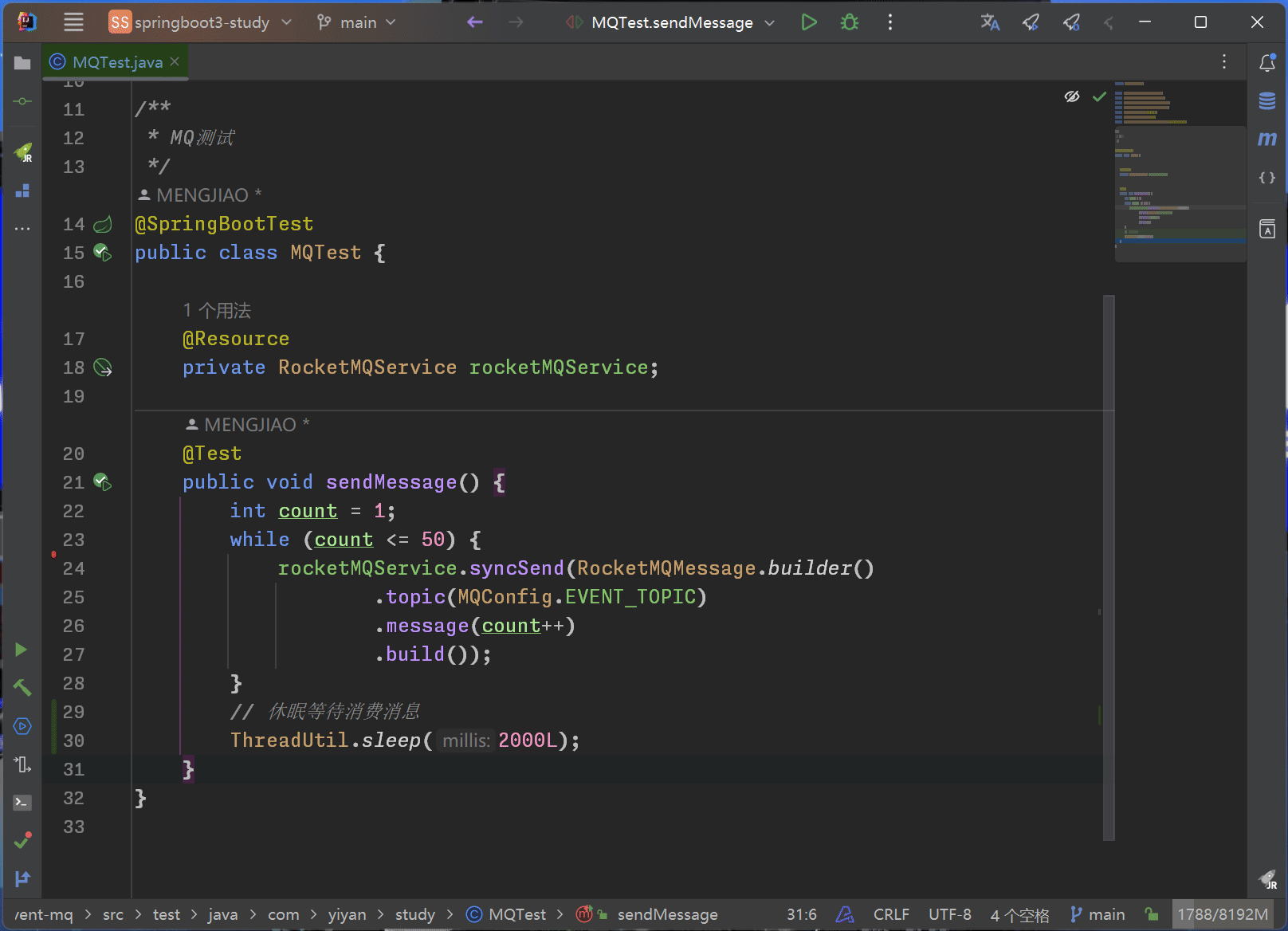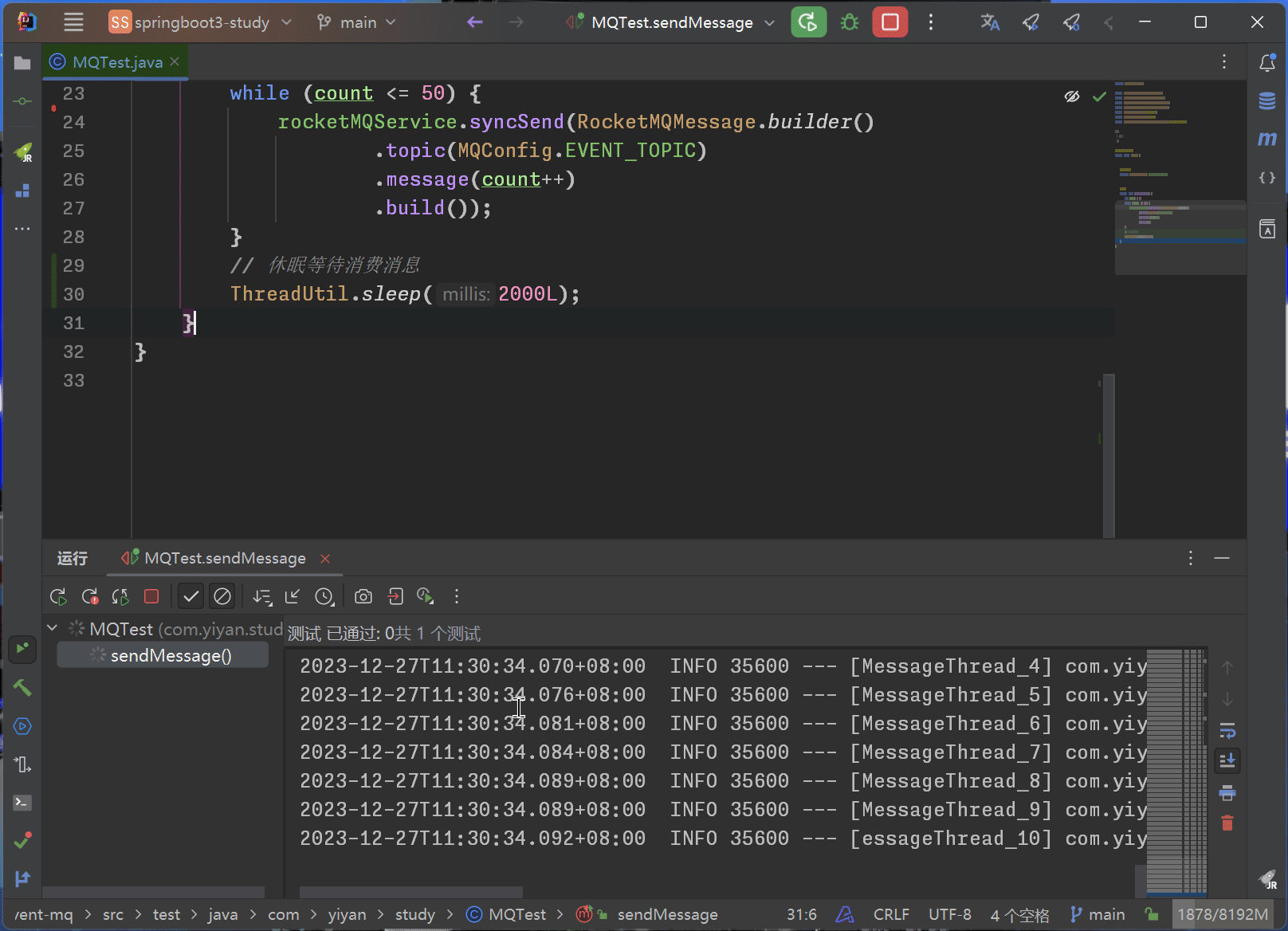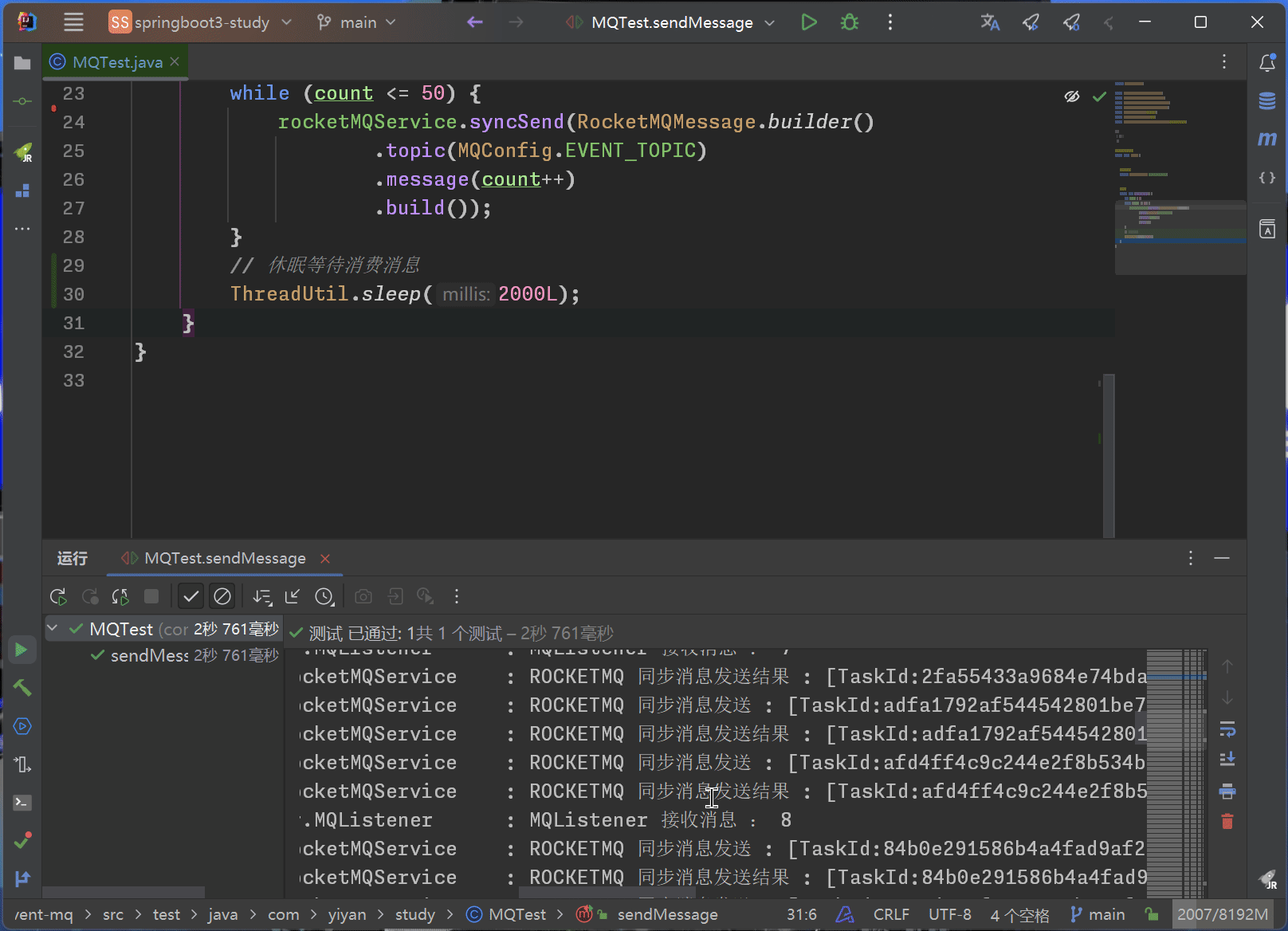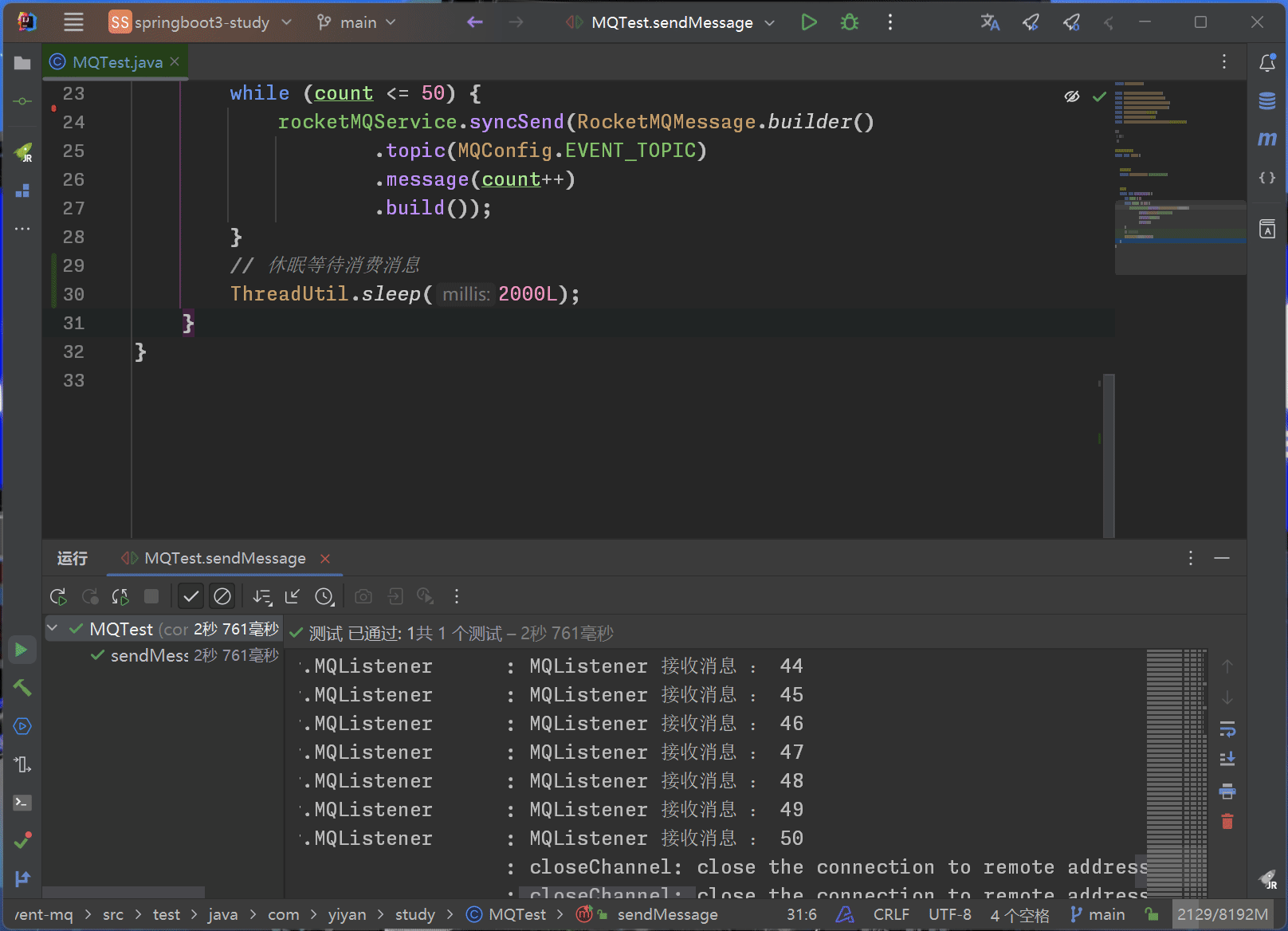
Spring Boot+RocketMQ 实现多实例分布式环境下的事件驱动
为什么要使用MQ? 在Spring Boot Event这篇文章中已经通过Guava或者SpringBoot自身的Listener实现了事件驱动,已经做到了对业务的解耦。为什么还要用到MQ来进行业务解耦呢? 首先无论是通过Guava还是Spring Boot自身提供的监听注解来实现的事…...

oracle ORA-01704: string literal too long ORACLE数据库clob类型
当oracle数据表中有clob类型字段时候,insert或update的sql语句中,超过长度就会报错 ORA-01704: string literal too long update xxx set xxx <div><h1>123</h1></div> where id 100;可以修改为 DECLAREstr varchar2(10000…...
微星主板强刷BIOS(以微星X370gaming plus 为例)
(前两天手欠,用U盘通过微星的M-flash升级BIOS 升级过程中老没动静就强制关机了 然后电脑就打不开了) 几种强刷主板BIOS的方式 在网上看到有三种强刷BIOS的方式分别是: 使用夹子编程器 (听说不太好夹)使用微星转接线编程器(只能用于微星主板࿰…...

matlab 图像上生成指定中心,指定大小的矩形窗
用matlab实现在图像上生成指定中心,指定大小的矩形窗(奇数*奇数) function PlaneWin PlaneWindow(CentreCoorX,CentreCoorY,RadiusX,RadiusY,SizeImRow,SizeImColumn) % 在图像上生成指定中心,指定大小的矩形窗(奇数*奇数) % % Input: % CentreCoorX(1*1) % CentreCoorY(1*1)…...
❀My学习小记录之算法❀
目录 算法:) 一、定义 二、特征 三、基本要素 常用设计模式 常用实现方法 四、形式化算法 五、复杂度 时间复杂度 空间复杂度 六、非确定性多项式时间(NP) 七、实现 八、示例 求最大值算法 求最大公约数算法 九、分类 算法:) 一、定义 …...

Hive-high Avaliabl
hive—high Avaliable hive的搭建方式有三种,分别是 1、Local/Embedded Metastore Database (Derby) 2、Remote Metastore Database 3、Remote Metastore Server 一般情况下,我们在学习的时候直接使用hive –service metastore的方式…...
码住!8个小众宝藏的开发者学习类网站
1、simplilearn simplilearn是全球排名第一的在线学习网站,它的课程由世界知名大学、顶级企业和领先的行业机构通过实时在线课程设计和提供,其中包括顶级行业从业者、广受欢迎的培训师和全球领导者。 2、VisuAlgo VisuAlgo是一个免费的在线学习算法和数…...

Postman常见问题及解决方法
1、网络连接问题 如果Postman无法发送请求或接收响应,可以尝试以下操作: 检查网络连接是否正常,包括检查网络设置、代理设置等。 确认请求的URL是否正确,并检查是否使用了正确的HTTP方法(例如GET、POST、PUT等&#…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
