最短路径(数据结构实训)(难度系数100)
最短路径
描述:
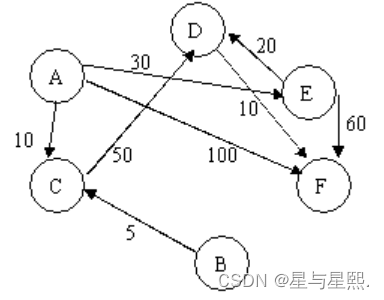
已知一个城市的交通路线,经常要求从某一点出发到各地方的最短路径。例如有如下交通图:
则从A出发到各点的最短路径分别为:
B:0
C:10
D:50
E:30
F:60输入:
输入只有一个用例,第一行包括若干个字符,分别表示各顶点的名称,接下来是一个非负的整数方阵,方阵维数等于顶点数,其中0表示没有路,正整数表示两点之间边的长度。可以假定该图为有向图。
最后一行为要求的出发点。输出:
输出从已知起点到各顶点的最短路径长度。输出格式是根据顶点输入顺序,依次输出其最智短路径长度。各顶点分别用一行输出,先输出目标顶点,然后一冒号加一个空格,最后是路径长度。0表示没有路。
样例输入:
ABCDEF
0 0 10 0 30 100
0 0 5 0 0 0
0 0 0 50 0 0
0 0 0 0 0 10
0 0 0 20 0 60
0 0 0 0 0 0
A
样例输出:
B: 0
C: 10
D: 50
E: 30
F: 60
方法一(Floyd算法):
import java.util.Scanner;public class Xingyuxingxi
{public static void main(String[] args){Scanner sc=new Scanner(System.in);String str=sc.next();int n=str.length();int [][]dt=new int[n][n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {dt[i][j]=sc.nextInt();if(dt[i][j]==0&&i!=j) {dt[i][j]=5000000;//因为题目数据范围有限,所以用5000000代替最大值,也可以用别的数代替}}}char a=sc.next().charAt(0);for(int k=0;k<n;k++){//floyd算法的简单之处,只需要三层循环,就能遍历出所有点到所有点的最短距离,如果范围过大就不要用floyd算法了for(int i=0;i<n;i++){for(int j=0;j<n;j++){dt[i][j]=Math.min(dt[i][j],dt[i][k]+dt[k][j]);//更新最短路径}}}int g=0;for(int i=0;i<n;i++) {if(str.charAt(i)==a) {//找到起始点的下标g=i;break;}}for (int i = 0; i < n; i++) {if(dt[g][i]==5000000)dt[g][i]=0;//如果为最大值表示没有路,题目要求用0表示没有路if(str.charAt(i)!=a)//如果不是起始点则输出最短距离System.out.printf("%c: %d\n",str.charAt(i),dt[g][i]);}}
}方法二(Dijkstra算法):
import java.util.Scanner;public class Xingyuxingxi
{public static void main(String[] args){Scanner sc=new Scanner(System.in);String str=sc.next();int n=str.length();int [][]dt=new int[n][n];int []dist=new int[n];//储存选定起点到其他点的距离boolean []st=new boolean[n];//储存该点是否遍历过到其他点的距离for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {dt[i][j]=sc.nextInt();if(dt[i][j]==0&&i!=j) {dt[i][j]=5000000;//用5000000代替最大值Integer.MAX_VALUE}}}char a=sc.next().charAt(0);for (int i = 0; i < n; i++) {dist[i]=5000000;}int g=0;for(int i=0;i<n;i++) {if(str.charAt(i)==a){//找到起点下标g=i;break;}}dist[g]=0;for (int i = 0; i < n; i++) {int t=-1;for(int j=0;j<n;j++) {if(!st[j]&&(t==-1||dist[t]>dist[j])){//找到每次更新路线后t到起点的最短距离的点t=j;}}st[t]=true;for(int j=0;j<n;j++){//更新距离,各个点到t的距离dist[j]=Math.min(dist[j],dist[t]+dt[t][j]);}}for (int i = 0; i < n; i++) {if(dist[i]==5000000)dist[i]=0;//如果为最大值表示没有路,题目要求用0代替没有通路if(i!=g)System.out.printf("%c: %d\n",str.charAt(i),dist[i]);}}
}关于为什么用5000000代替Integer.MAX_VALUE
因为题目中涉及到最大值的计算,如果使用Integer.MAX_VALUE加任意一个数的话就会变为负数,求最小值的话就会一直是Integer.MAX_VALUE+其他数的和,我自己写的时候每次加都会变成负数,所以就把最大值改小了,本题数据并不强,可以用一个足够大的数代替这个最大值即可,不一定非得是5000000
相关文章:
最短路径(数据结构实训)(难度系数100)
最短路径 描述: 已知一个城市的交通路线,经常要求从某一点出发到各地方的最短路径。例如有如下交通图: 则从A出发到各点的最短路径分别为: B:0 C:10 D:50 E:30 F:60 输…...
基于SSM实现的电动汽车充电网点管理系统
一、系统架构 前端:jsp | jquery | bootstrap | css 后端:spring | springmvc | jdbc 环境:jdk1.8 | mysql 二、代码及数据库 三、功能介绍 01. web端-首页 02. web端-登录 03. web端-注册 04. web端-我要充电 05. web端-个人中心-消…...
Android ImageView如何使用.svg格式图片
我们知道imageview常用的图片格式是.jpg/.png或者drawable里的部分.xml文件。但有时UI会给过来.svg格式的文件,下面讲解如何使用.svg格式图片文件 step1:AS点击File -> New -> Vector Asset step2:选中要使用的.svg文件,按需要命名和调整&#x…...

力扣热题100道-子串篇
字串 560.和为K的子数组 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。 子数组是数组中元素的连续非空序列。 示例 1: 输入:nums [1,1,1], k 2 输出:2示例 2: 输入&a…...

day3--Shell
1.shell语法 概论 概论 shell是我们通过命令行与操作系统沟通的语言。shell脚本可以直接在命令行中执行,也可以将一套逻辑组织成一个文件,方便复用。 AC Terminal中的命令行可以看成是一个“shell脚本在逐行执行”。Linux中常见的shell脚本有很多种&…...

【数据结构】插入排序、选择排序、冒泡排序、希尔排序、堆排序
前言:生活中我们总是会碰到各种各样的排序,今天我们就对部分常用的排序进行总结和学习,今天的内容还是相对比较简单的一部分,各位一起加油哦! 💖 博主CSDN主页:卫卫卫的个人主页 💞 ὄ…...

TiDB 7.5 LTS 发版丨提升规模化场景下关键应用的稳定性和成本的灵活性
互联网时代,数据的迅猛增长给数据库带来了可扩展性的挑战,Gen AI 带来的数据暴增更加剧了这种挑战。传统的数据分片已经不能承载新时代数据暴增的需求,更简单且具有前瞻性的方法则是采用原生分布式数据库来解决扩展性问题。在这种规模化场景的…...
服务器数据恢复-误操作导致xfs分区数据丢失的数据恢复案例
服务器数据恢复环境: 某品牌OceanStorT系列某型号存储MD1200磁盘柜,组建的raid5磁盘阵列。上层分配了1个lun,安装的linux操作系统,划分两个分区,分区一通过lvm进行扩容,分区二格式化为xfs文件系统。 服务器…...
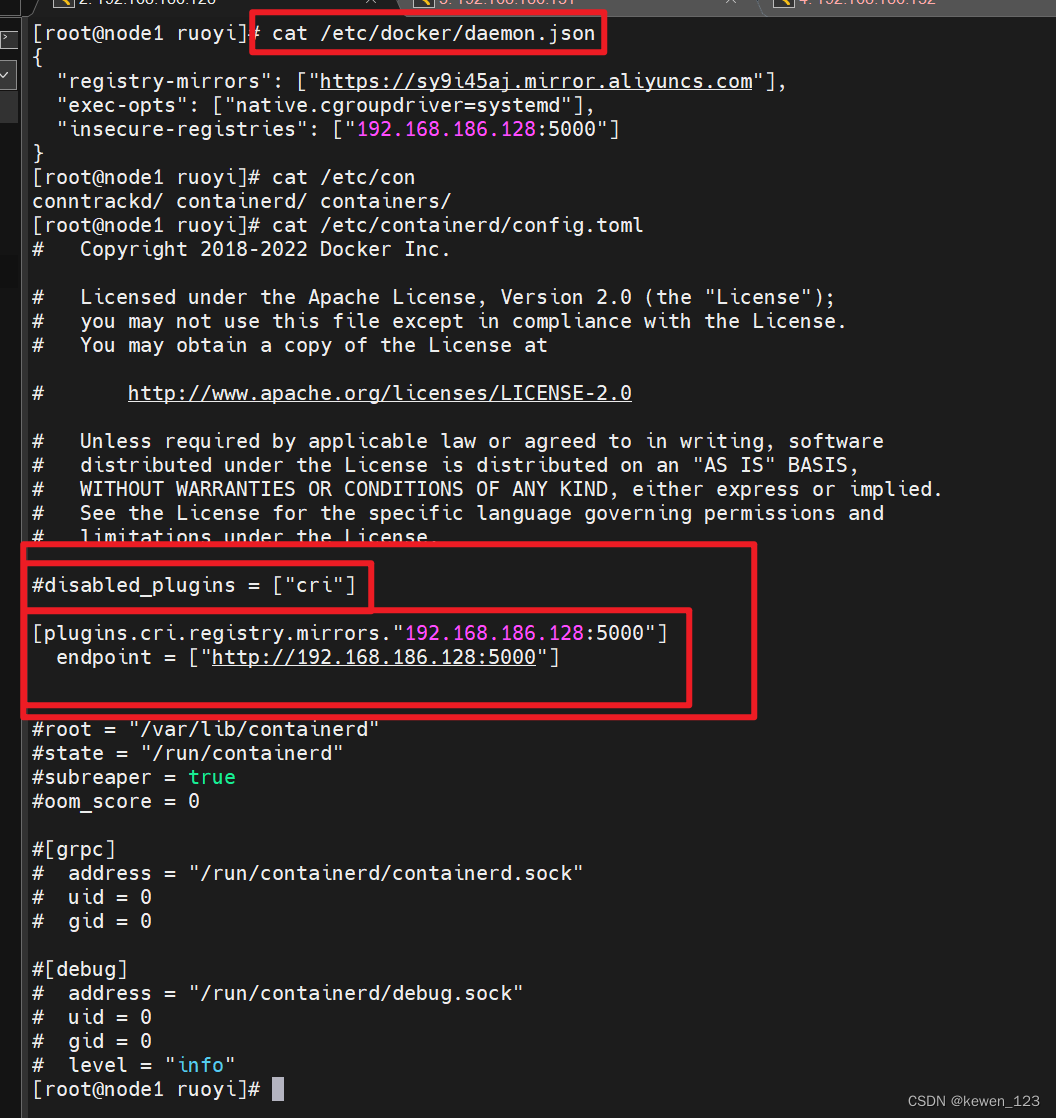
安装Kubernetes1.23、kubesphere3.4、若依项目自动打包部署到K8S记录
1.安装kubernetes1.23详细教程 kubernetes(k8s)集群超级详细超全安装部署手册 - 知乎 2.安装rancher动态存储 kubectl apply -f https://raw.githubusercontent.com/rancher/local-path-provisioner/master/deploy/local-path-storage.yaml3.安装kubesphere3.4 准备工作 您…...
 `MaterializedMySQL`同步机制解读)
(三) `MaterializedMySQL`同步机制解读
当使用 ClickHouse 的 MaterializedMySQL 引擎进行全量同步时,它主要依赖于两个关键机制:初始全量数据导入和随后的增量更新。以下是这些机制的详细解释: 初始全量数据导入 读取现有数据: 当您在 ClickHouse 中创建一个 MaterializedMySQL 类…...
)
使用 stream 流构建树(不使用递归)
你知道的越多,你不知道的越多 点赞再看,养成习惯 如果您有疑问或者见解,欢迎指教: 企鹅:869192208 文章目录 前言代码实现定义测试实体类实现方法 前言 最近遇到一个地区数据需要转换成树的需求,研究了一种…...

docker 部署 个人网页版 wps office
先声明一下,这个是用的linux桌面,然后安装了一个wps软件 安装好之后,通过我们自己的浏览器进行操作。。。。。 我只是试了一下,目前发现只能一个人用,里面还有谷歌浏览器,就是一个远程linux桌面 docker …...
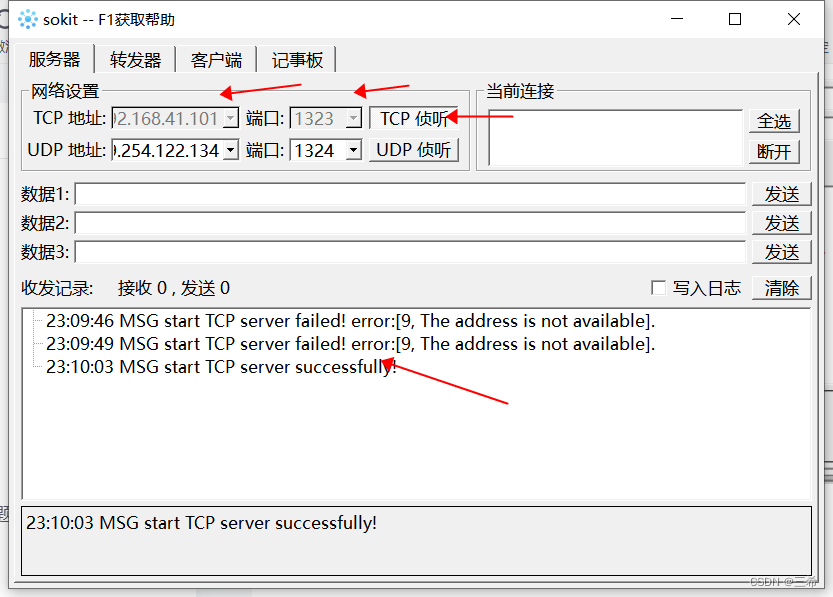
windows进行udp端口转发,解决项目中服务器收不到组播数据的问题
说明 windows7的netsh interface portproxy命令只支持tcp端口转发 如果要进行udp端口转发可以使用sokit 运行sokit 端口转发(以为tcp作为讲解,udp类似) 选择转发器 输入监听地址(SRC地址)和端口 输入转发地址&am…...

抖音、小红书、视频号是如何判定是否限流的?
在这个新媒体营销的时代,抖音、小红书和视频号作为中国最受欢迎的社交媒体平台,为品牌和内容创作者提供了极具潜力的展示空间。然而,无论在哪个平台,限流成为很多人的苦恼。 抖音的推荐算法基于人群画像和初始流量池,同…...
)
frida native hook 技术( frida hook so层函数)
什么是hook: hook,中文译作”钩子“,”挂钩“,看起来好像和钓鱼有点关系,其实它更像一张网。想象这样一个场景:我们在河流上筑坝,只留一个狭窄的通道让水流通过,在这个通道上设一张网…...
-- 多环境开发(yml多文件版))
SpringBoot运维(三)-- 多环境开发(yml多文件版)
目录 引言: 1. 多环境开发的配置 2. 多环境开发--根据功能拆分配置文件 引言: 多环境? 其实就是说你的电脑上写的程序最终要放到别人的服务器上去运行。每个计算机环境不一样...

Vue 修饰符有哪些
事件修饰符 .stop 阻止事件继续传播.prevent 阻止标签默认行为.capture 使用事件捕获模式, 即元素自身触发的事件先在此处处理,然后才交由内部元素进行处理.self 只当在 event.target 是当前元素自身时触发处理函数.once 事件将只会触发一次.passive 告诉浏览器你不…...
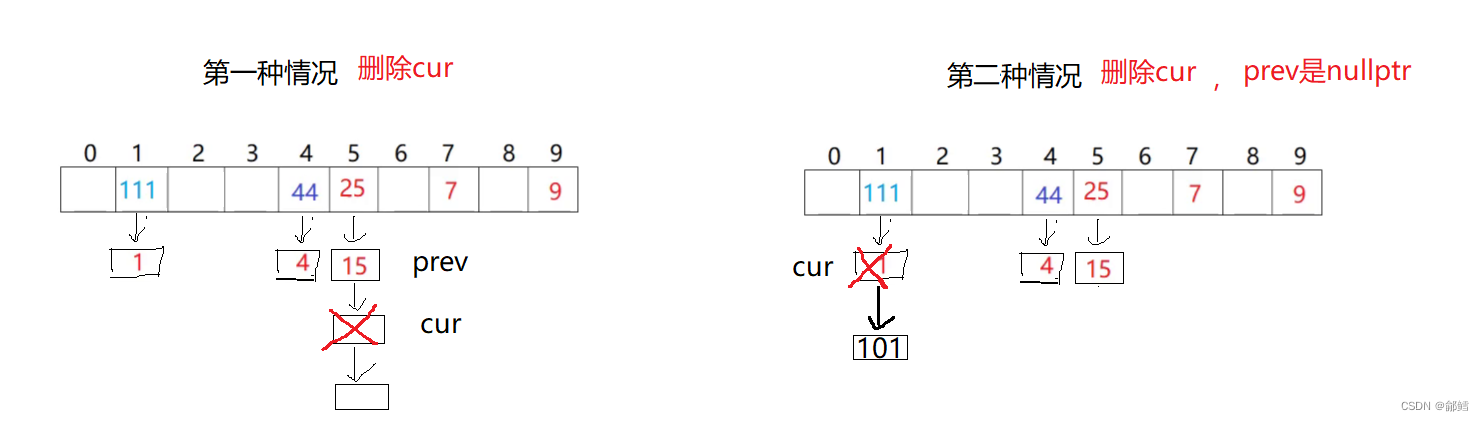
哈希桶的模拟实现【C++】
文章目录 哈希冲突解决闭散列 (开放定址法)开散列 (链地址法、哈希桶)开散列实现(哈希桶)哈希表的结构InsertFindErase 哈希冲突解决 闭散列 (开放定址法) 发生哈希冲突时…...
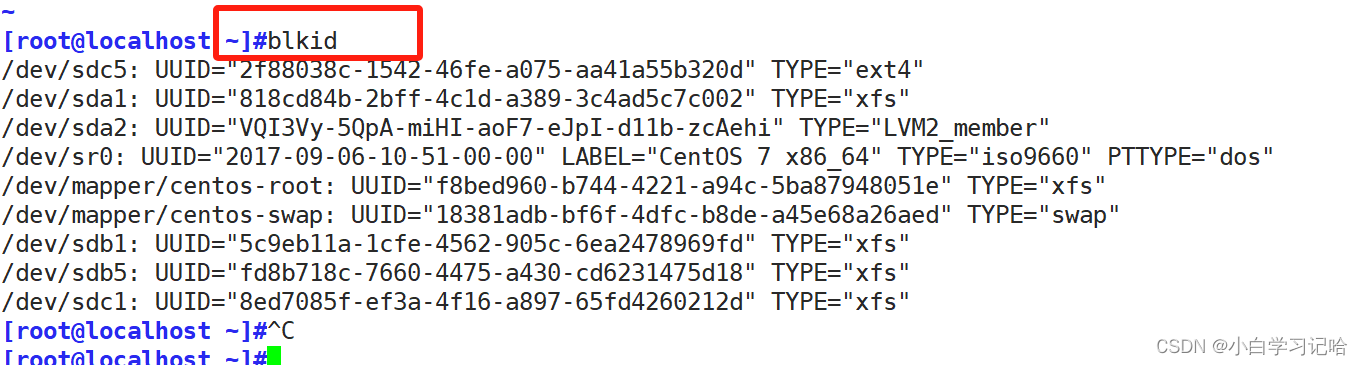
磁盘相关知识
一、硬盘数据结构 1.扇区: 盘片被分为多个扇形区域,每个扇区存放512字节的数据(扇区越多容量越大) 存放数据的最小单位 512字节 (硬盘最小的存储单位是扇区,512 个字节,八个扇区组成一块&…...

FTP原理与配置
FTP是用来传送文件的协议。使用FTP实现远程文件传输的同时,还可以保证数据传输的可靠性和高效性。 FTP的应用 FTP 提供了一种在服务器和客户机之间上传和下载文件的有效方式。在企业网络中部署一台FTP服务器,将网络设备配置为FTP客户端,则可…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
