哈希桶的模拟实现【C++】
文章目录
- 哈希冲突解决
- 闭散列 (开放定址法)
- 开散列 (链地址法、哈希桶)
- 开散列实现(哈希桶)
- 哈希表的结构
- Insert
- Find
- Erase
哈希冲突解决
闭散列 (开放定址法)
发生哈希冲突时,如果哈希表未被装满,说明在哈希表种必然还有空位置,那么可以把产生冲突的元素存放到冲突位置的“下一个”空位置中去
如何寻找“下一个位置”
1、线性探测
发生哈希冲突时,从发生冲突的位置开始,依次向后探测,直到找到下一个空位置为止
Hi=(H0+i)%m ( i = 1 , 2 , 3 , . . . )
H0:通过哈希函数对元素的关键码进行计算得到的位置。
Hi:冲突元素通过线性探测后得到的存放位置
m:表的大小。
举例:
用除留余数法将序列{1,111,4,7,15,25,44,9}插入到表长为10的哈希表中,当发生哈希冲突时我们采用闭散列的线性探测找到下一个空位置进行插入,插入过程如下:
使用除留余数法
1%10 =1 ,111 %10 =1
即111和1发生了哈希冲突 ,所以111找到1的下一个空位置插入

将数据插入到有限的空间,那么空间中的元素越多,插入元素时产生冲突的概率也就越大,冲突多次后插入哈希表的元素,在查找时的效率必然也会降低。
介于此,哈希表当中引入了负载因子(载荷因子):
负载因子 = 表中有效数据个数 / 空间的大小
不难发现:
负载因子越大,产出冲突的概率越高,查找的效率越低
负载因子越小,产出冲突的概率越低,查找的效率越高
负载因子越小,也就意味着空间的利用率越低,此时大量的空间都被浪费了。对于闭散列(开放定址法)来说,负载因子是特别重要的因素,一般控制在0.7~0.8以下
采用开放定址法的hash库,如JAVA的系统库限制了负载因子为0.75,当超过该值时,会对哈希表进行增容
线性探测的缺点:一旦发生冲突,所有的冲突连在一起,容易产生数据“堆积”,即不同关键码占据了可利用的空位置,使得寻找某关键码的位置需要多次比较(踩踏效应),导致搜索效率降低
2、二次探测
二次探测为了避免该问题,找下一个空位置的方法为
Hi=(H0+i ^2 )%m ( i = 1 , 2 , 3 , . . . )
H0:通过哈希函数对元素的关键码进行计算得到的位置
Hi:冲突元素通过二次探测后得到的存放位置
m:表的大小
相比线性探测而言,二次探测i是平方,采用二次探测的哈希表中元素的分布会相对稀疏一些,不容易导致数据堆积
template <class K>
struct DefaultHashFunc
{size_t operator() (const K& key){return (size_t)key;}
};template <>
struct DefaultHashFunc<string>
{size_t operator() (const string& str){//BKDR,将输入的字符串转换为哈希值size_t hash = 0;for (auto ch : str){hash *= 131;hash += ch;}return hash;}
};namespace open_address
{enum STATE{EXIST,EMPTY,DELETE};template<class K, class V>struct HashData{pair<K, V> _kv;STATE _state = EMPTY;};struct StringHashFunc{size_t operator()(const string& str){return str[0];}};//template<class K, class V>template<class K, class V, class HashFunc = DefaultHashFunc<K>>class HashTable{public:HashTable(){_table.resize(10);}bool insert(const pair<K, V> kv){//扩容 if ((double)_n / (double)_table.size() >= 0.7){HashTable<K, V> newHT;size_t newSize = _table.size() * 2;newHT._table.resize(newSize);//遍历旧表的数据,将旧表的数据重新映射到新表中for (size_t i = 0; i < _table.size(); i++){if (_table[i]._state == EXIST){newHT.insert(_table[i]._kv);//插入的写成kv不行?}}_table.swap(newHT._table);}//线性探测HashFunc hf;size_t hashi = hf(kv.first) % _table.size();//如果该位置没有元素,则直接插入元素 ,如果该位置有元素,找到下一个空位置,插入新元素while (_table[hashi]._state == EXIST)//不是EMPTY和DELETE这两种情况{++hashi;hashi %= _table.size();}//是EMPTY和DELETE这两种情况_table[hashi]._kv = kv;_table[hashi]._state = EXIST;++_n;return true;}HashData<const K, V>* Find(const K& key){HashFunc hf;//线性探测 //如果该位置没有元素,则直接插入元素 ,如果该位置有元素,找到下一个空位置,插入新元素size_t hashi = hf(key) % _table.size();while (_table[hashi]._state != EMPTY) //DELETE和EXIST{if (_table[hashi]._state == EXIST && _table[hashi]._kv.first == key){return (HashData<const K, V>*) & _table[hashi];}}return nullptr;}bool Erase(const K& key){//先找到HashData<const K, V>* ret = Find(key);//再删除 if (ret != nullptr){ret->_state = DELETE;_n--;return true;}//没找到 return false;}public:vector<HashData<K, V>> _table;size_t _n = 0; //存储有效数据的个数};}
闭散列最大的缺陷就是空间利用率比较低,这也是哈希的缺陷
开散列 (链地址法、哈希桶)
开散列,又叫哈希桶,首先对关键码集合用哈希函数计算哈希地址,具有相同地址的关键码归于同一子集合,每一个子集合称为一个桶,各个桶中的元素通过一个单链表链接起来,各链表的头结点存储在哈希表中
举例:
用除留余数法将序列{1,111,4,7,15,25,44,9}插入到表长为10的哈希表中,当发生哈希冲突时我们采用开散列的方式进行插入,插入过程如下:

将相同哈希地址的元素通过单链表链接起来,然后将链表的头结点存储在哈希表中的方式,不会影响与自己哈希地址不同的元素的增删查改的效率,因此开散列的负载因子相比闭散列而言,可以稍微大一点
闭散列的开放定址法,负载因子不能超过1,一般建议控制在[0.0, 0.7]
开散列的哈希桶,负载因子可以超过1,一般建议控制在[0.0, 1.0]
在实际中,开散列的哈希桶结构比闭散列更实用,主要原因有两点:
哈希桶的负载因子可以更大,空间利用率高
哈希桶在极端情况下还有可用的解决方案
开散列实现(哈希桶)
哈希表的结构
struct HashNode{pair<K, V> _kv;HashNode<K,V>* _next;HashNode( const pair<K, V> & kv):_kv(kv),_next(nullptr){}};
Insert
bool Insert(const pair<K,V> & kv){size_t hashi = kv.first % _table.size();//负载因子到1就扩容 if (_n == _table.size()){size_t newsize = _table.size() * 2;vector<Node*> newTable;newTable.resize(newsize, nullptr);//遍历旧表,将原哈希表当中的结点插入到新哈希表for (int i = 0; i <= _table.size(); i++){Node* cur = _table[i];//插入到新哈希表while (cur != nullptr){Node* next = cur->_next;// 重新分配hashisize_t hashi = cur->_kv.first % _table.size();cur->_next = newTable[hashi];newTable[hashi] = cur;cur = next;}}}//头插 Node* newnode = new Node(kv);newnode->_next = _table[hashi];_table[hashi] = newnode;return true;}
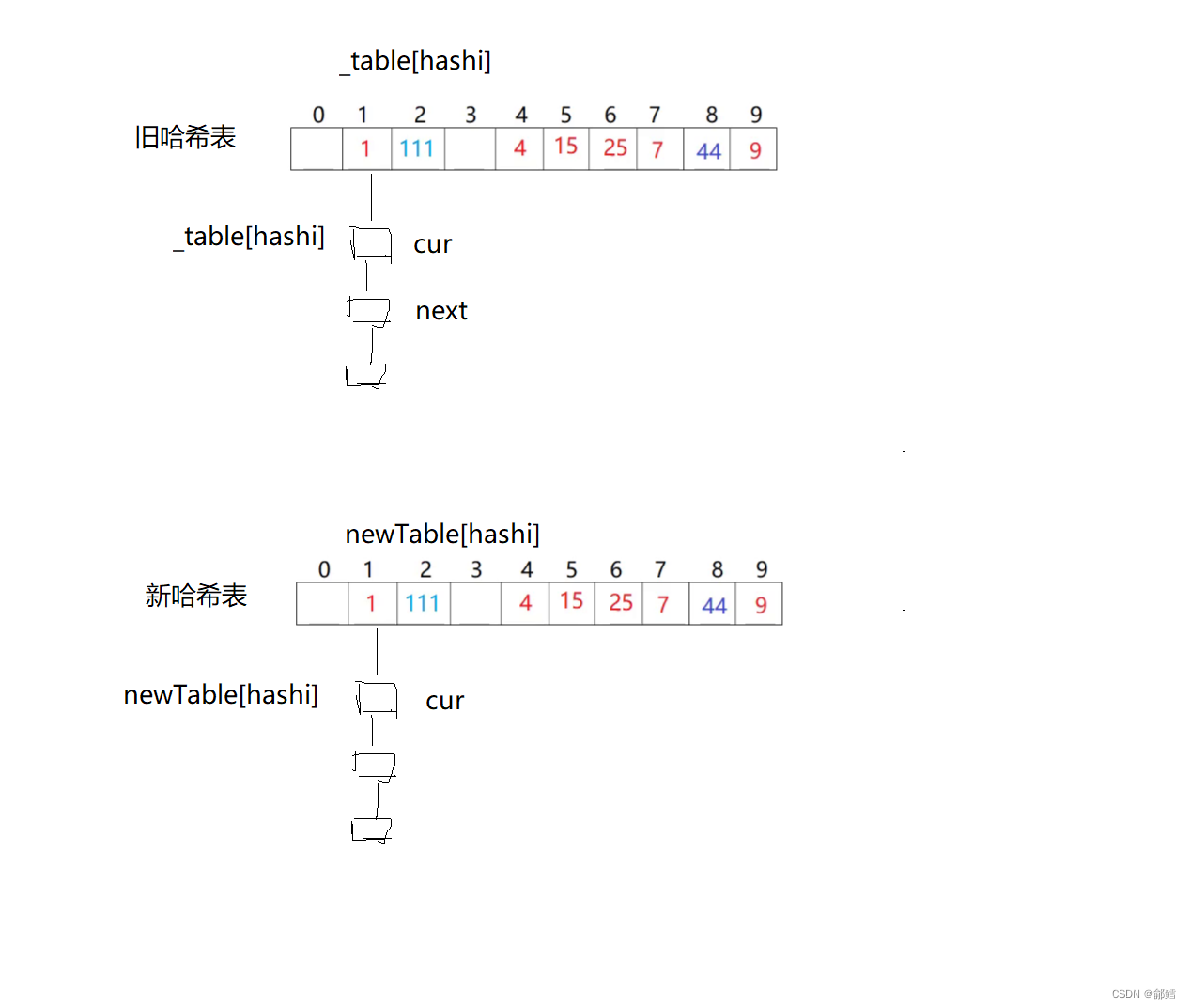
Find
Node * Find(const K & key){size_t hashi = key % _table.size();Node* cur = _table[hashi];while (cur != nullptr){if (key == cur->_kv.first){return cur;}cur = cur->_next;}return nullptr;}
Erase
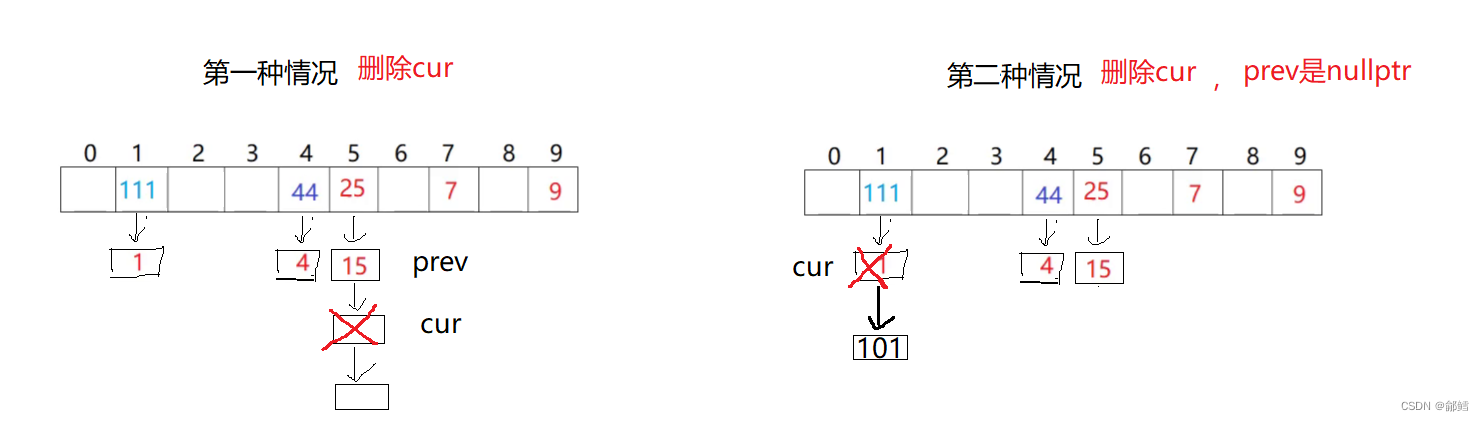
bool Erase(const K & key){size_t hashi = key % _table.size();Node* cur = _table[hashi];Node* prev = nullptr;while (cur != nullptr){if (key == cur->_kv.first){if(prev==nullptr)//第二种情况 ,prev是nullptr ,就是头删{_table[hashi] = cur->_next;}else//第一种情况 ,cur是头节点{prev->_next = cur->_next;}delete cur;return true; }prev = cur;cur = cur->_next;}//没找到 return false;}
namespace hash_bucket
{template <class K ,class V> struct HashNode{pair<K, V> _kv;HashNode<K,V>* _next;HashNode( const pair<K, V> & kv):_kv(kv),_next(nullptr){}};template<class K,class V> class HashTable{public:typedef HashNode<K,V> Node;//iterator begin()//{//}//iterator end()//{//}//const_iterator begin()//{//}//const_iterator end()//{//}//GetNextPrime()//{//}HashTable(){_table.resize(10, nullptr);}~HashTable(){}//bool Insert(const pair<K, V> kv)//{// //负载因子到1就扩容 // if (_n == _table.size())// {// size_t newsize = _table.size() * 2;// vector<Node*> newtable;// newtable.resize(newsize, nullptr);// }// size_t hashi = kv.first % _table.size();// //头插 // Node* newnode = new Node(key);// newnode->_next = _table[hashi];// _table[hashi] = newnode;// ++_n;// return true;//}bool Insert(const pair<K,V> & kv){size_t hashi = kv.first % _table.size();//负载因子到1就扩容 if (_n == _table.size()){size_t newsize = _table.size() * 2;vector<Node*> newTable;newTable.resize(newsize, nullptr);//遍历旧表,将原哈希表当中的结点插入到新哈希表for (int i = 0; i <= _table.size(); i++){Node* cur = _table[i];//插入到新哈希表while (cur != nullptr){Node* next = cur->_next;// 重新分配hashisize_t hashi = cur->_kv.first % _table.size();cur->_next = newTable[hashi];newTable[hashi] = cur;cur = next;}}}//头插 Node* newnode = new Node(kv);newnode->_next = _table[hashi];_table[hashi] = newnode;return true;}Node * Find(const K & key){size_t hashi = key % _table.size();Node* cur = _table[hashi];while (cur != nullptr){if (key == cur->_kv.first){return cur;}cur = cur->_next;}return nullptr;}bool Erase(const K & key){size_t hashi = key % _table.size();Node* cur = _table[hashi];Node* prev = nullptr;while (cur != nullptr){if (key == cur->_kv.first){if(prev==nullptr)//第二种情况 ,prev是nullptr ,就是头删{_table[hashi] = cur->_next;}else//第一种情况 ,cur是头节点{prev->_next = cur->_next;}delete cur;return true; }prev = cur;cur = cur->_next;}//没找到 return false;}void Print(){for (size_t i = 0; i < _table.size(); i++){printf("[%d]->", i);Node* cur = _table[i];while (cur != nullptr){cout << cur->_kv.first << "->";cur = cur->_next;}printf("NULL\n");}cout << endl;}private:vector<Node*> _table;//指针数组size_t _n = 0;//存储有效数据};
}
如果你觉得这篇文章对你有帮助,不妨动动手指给点赞收藏加转发,给鄃鳕一个大大的关注
你们的每一次支持都将转化为我前进的动力!!
相关文章:

哈希桶的模拟实现【C++】
文章目录 哈希冲突解决闭散列 (开放定址法)开散列 (链地址法、哈希桶)开散列实现(哈希桶)哈希表的结构InsertFindErase 哈希冲突解决 闭散列 (开放定址法) 发生哈希冲突时…...
磁盘相关知识
一、硬盘数据结构 1.扇区: 盘片被分为多个扇形区域,每个扇区存放512字节的数据(扇区越多容量越大) 存放数据的最小单位 512字节 (硬盘最小的存储单位是扇区,512 个字节,八个扇区组成一块&…...

FTP原理与配置
FTP是用来传送文件的协议。使用FTP实现远程文件传输的同时,还可以保证数据传输的可靠性和高效性。 FTP的应用 FTP 提供了一种在服务器和客户机之间上传和下载文件的有效方式。在企业网络中部署一台FTP服务器,将网络设备配置为FTP客户端,则可…...
ios环境搭建_xcode安装及运行源码
目录 1 xcode 介绍 2 xcode 下载 3 xocde 运行ios源码 1 xcode 介绍 Xcode 是运行在操作系统Mac OS X上的集成开发工具(IDE),由Apple Inc开发。Xcode是开发 macOS 和 iOS 应用程序的最快捷的方式。Xcode 具有统一的用户界面设计࿰…...

C++ 151. 反转字符串中的单词
给你一个字符串 s ,请你反转字符串中 单词 的顺序。 单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。 返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。 注意:输入字符串 s中可能会存在前导空格、尾随…...
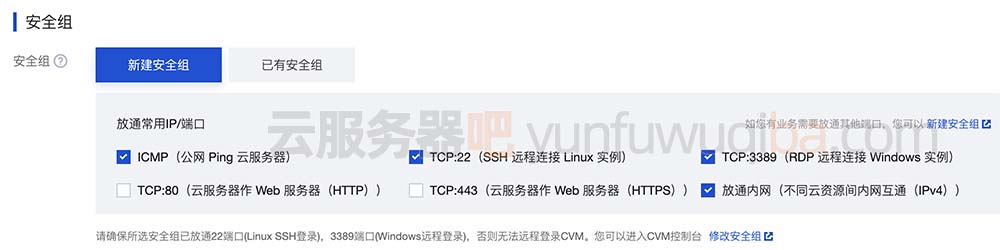
腾讯云服务器如何买(购买腾讯云服务器的详细步骤)
腾讯云服务器购买流程直接在官方秒杀活动上购买比较划算,在云服务器CVM或轻量应用服务器页面自定义购买价格比较贵,但是自定义购买云服务器CPU内存带宽配置选择范围广,活动上购买只能选择固定的活动机,选择范围窄,但是…...

48道Linux面试题
本博客将汇总 Linux 面试中常见的题目,并提供详细的解答。 文章目录 1、绝对路径用什么[符号表](https://so.csdn.net/so/search?q符号表&spm1001.2101.3001.7020)示?当前目录、上层目录用什么表示?主目录用什么表示? 切换目录用什么命…...

(13)Linux 进程的优先级、进程的切换以及环境变量等
前言:我们先讲解进程的优先级。然后讲解进程的切换,最后我们讲解环境变量,并且做一个 "让自己的可执行程序不带路径也能执行"的实践,讲解环境变量的到如何删除,最后再讲几个常见的环境变量。 一、进程优先级…...
C卷 (JavaPythonNode.jsC++))
数的分解(100%用例)C卷 (JavaPythonNode.jsC++)
给定一个正整数n,如果能够分解为m(m >1)个连续正整数之和,请输出所有分解中,m最小的分解。 如果给定整数无法分解为连续正整数,则输出字符串"N" 输入描述 输入数据为一整数,范围为 (1,2^30] 输出描述 比如输入为: 21 输出: 21=10+11 示例1 输入输出示例…...
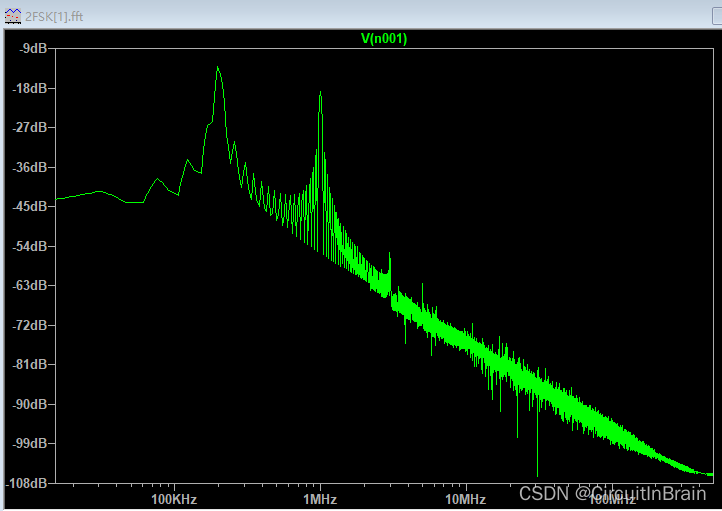
数字调制学习总结
调制:将基带的信号的频谱搬移到指定的信道通带内的过程。 解调:把指定信号通带内的信号还原为基带的过程。 1、2ASK调制 原理如下图所示,基带信号为单极不归零码,与载波信号相乘,得到调制信号。 调制电路可以用开关…...
AcWing 1129. 热浪(单源最短路)
题目链接 https://www.acwing.com/problem/content/1131/https://www.acwing.com/problem/content/1131/ 题解 此题属于单源最短路问题,根据数据范围,可以使用Dijkstra算法、堆优化版的Dijkstra算法、SPFA算法。本例采用SPFA算法,使用手写循…...
)
Mybatis Mapper XML文件-缓存(cache)
MyBatis包含一个强大的事务查询缓存特性,可以进行灵活的配置和自定义。在MyBatis 3的缓存实现中进行了许多改进,使其更加强大且更易于配置。 默认情况下,仅启用了本地会话缓存,该缓存仅用于缓存会话期间的数据。要启用全局的第二…...
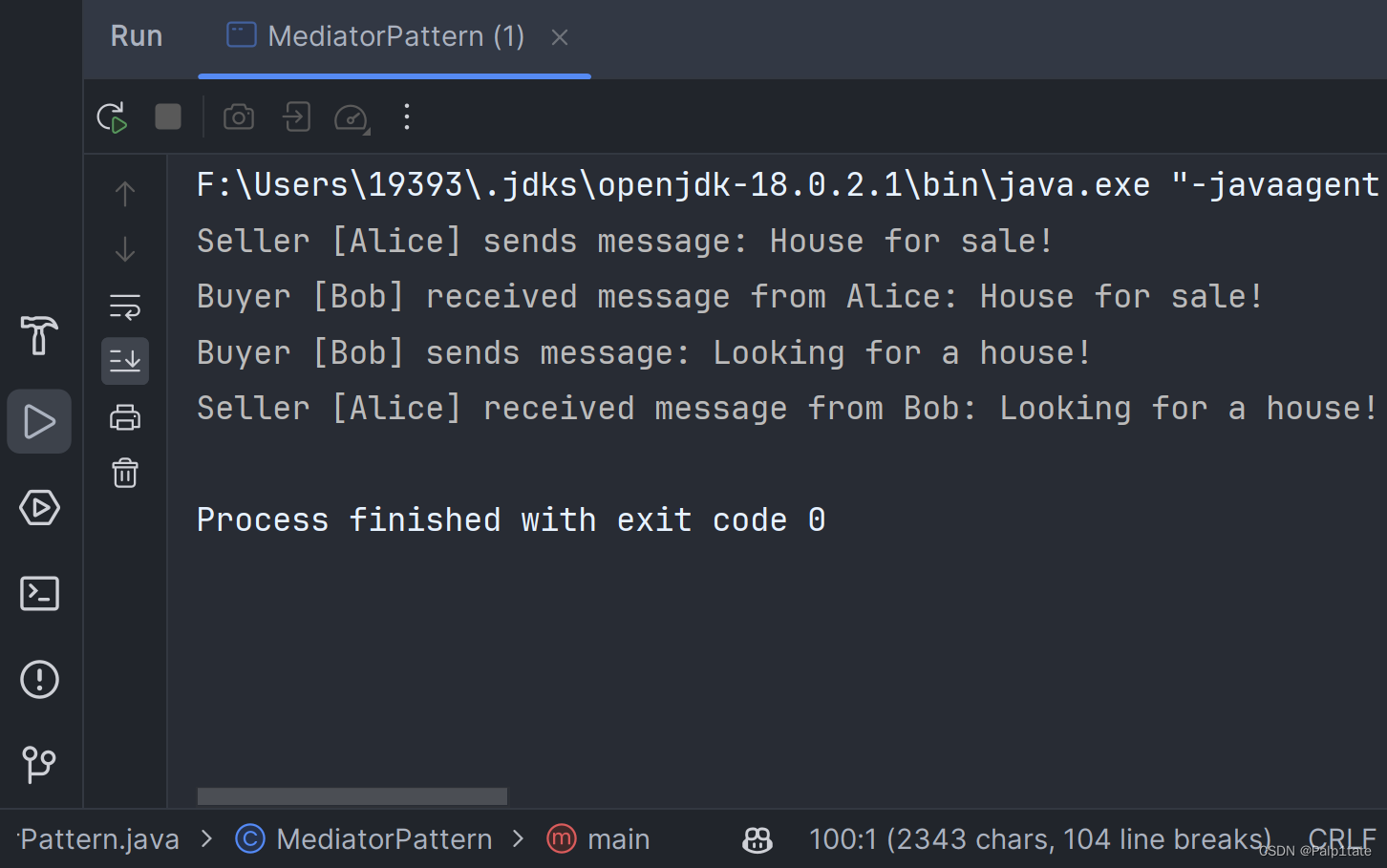
电子科大软件系统架构设计——设计模式
设计模式概述 设计模式的背景 设计面向对象软件比较困难,而设计可以复用的面向对象软件更加困难不是解决任何问题都需要从头做起,最好能复用以往的设计方案经验面向对象软件设计经验需要有一定的模式记录下来,以提供给其他设计者使用&#…...

ubuntu20 安装缺失的字体
在/usr/share/fonts创建文件夹winfonts sudo mkdir winfonts 下载缺失的字体后,复制命令到对应的文件夹。 刷新字体库 sudo mkfontscale sudo mkfontdir sudo fc-cache...

2023年12月27日学习记录_加入噪声
目录 1、今日计划学习内容2、今日学习内容1、add noise to audio clipssignal to noise ratio(SNR)加入 additive white gaussian noise(AWGN)加入 real world noises 2、使用kaggel上的一个小demo:CNN模型运行时出现的问题调整采样率时出现bug 3、明确90dB下能否声…...

Java面试题86-95
86. Java代码查错(4)public class Something { public int addOne(final int x) { return x; }}此代码有错误吗?答案: 错。int x被修饰成final,意味着x不能在addOne method中被修改。87. Java代码查错(5&…...

看完谁再说搞不定上下角标?
一、需求 开发中有一些需要用到上下角标的地方,比如说化学式、数学式、注释。。。除了可以使用上下角标的标签,还可以通过css样式和CV大法实现,以下是具体实现方式。 二、实现方法 (1)标签写法: <sup…...

在 Python 中使用装饰器decorator的 7 个层次
在 Python 中使用装饰器的 7 个层次(7 Levels of Using Decorators in Python) 文章目录 在 Python 中使用装饰器的 7 个层次(7 Levels of Using Decorators in Python)导言Level 0: 了解基本概念Basic Concepts和用法Usages什么是装饰器decorator?我们为什么需要装…...

Vue.js项目部署至Linux服务器的详细步骤
引言 在现代Web开发中,Vue.js作为一款流行的前端框架,为开发者提供了灵活且高效的工具。然而,在将Vue.js项目成功部署到Linux服务器上,可能需要一些额外的步骤和注意事项。本文将深入介绍在Linux服务器上部署Vue.js项目的详细步骤…...

Java三层架构/耦合/IOC/DI
一.三层架构 controller/web 控制层。接收前端发送的请求,对请求进行处理,并响应数据。 service 业务逻辑层,处理具体的业务逻辑。 dao 数据访问层(Data Access Object),也称为持久层。负责数据访问操作,包括数据的增、…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
