C++ 151. 反转字符串中的单词
给你一个字符串 s ,请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意:输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
示例 1:
输入:s = “the sky is blue”
输出:“blue is sky the”
示例 2:
输入:s = " hello world "
输出:“world hello”
解释:反转后的字符串中不能存在前导空格和尾随空格。
示例 3:
输入:s = “a good example”
输出:“example good a”
解释:如果两个单词间有多余的空格,反转后的字符串需要将单词间的空格减少到仅有一个。
提示:
1 <= s.length <= 104
s 包含英文大小写字母、数字和空格 ’ ’
s 中 至少存在一个 单词
class Solution {
public:string reverseWords(string s) {vector<string> res;s = s.substr(s.find_first_not_of(' '), s.find_last_not_of(' ') + 1);// 使用 istringstream 进行字符串分割istringstream iss(s);string word;while (iss >> word) {res.push_back(word);}// 逆序拼接结果字符串string result;for (int i = res.size() - 1; i >= 0; i--) {if (i > 0) result += res[i] + ' ';else result += res[i];}return result;}
};
一开始按照最笨的方式写的,结果MLE了,贴在这里谨记:
vector<string> res;int i = 0;while (i < s.size() && s[i] == ' ') i++;int j = s.size() - 1;while (j >= 0 && s[j] == ' ') j--;s = s.substr(i, j - i + 1);cout<<s<<endl;for(int i = 0; i < s.size(); i ++) {int j = i;while(j < s.size() && s[j] != ' ') j ++;res.push_back(s.substr(i, j - i));j --;while(s[j] == ' ') j ++;i = j;}string ss;for(int i = res.size() - 1; i >= 0; i --) {if(i > 0) ss += res[i] + ' ';else ss += res[i];}
相关文章:

C++ 151. 反转字符串中的单词
给你一个字符串 s ,请你反转字符串中 单词 的顺序。 单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。 返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。 注意:输入字符串 s中可能会存在前导空格、尾随…...
腾讯云服务器如何买(购买腾讯云服务器的详细步骤)
腾讯云服务器购买流程直接在官方秒杀活动上购买比较划算,在云服务器CVM或轻量应用服务器页面自定义购买价格比较贵,但是自定义购买云服务器CPU内存带宽配置选择范围广,活动上购买只能选择固定的活动机,选择范围窄,但是…...

48道Linux面试题
本博客将汇总 Linux 面试中常见的题目,并提供详细的解答。 文章目录 1、绝对路径用什么[符号表](https://so.csdn.net/so/search?q符号表&spm1001.2101.3001.7020)示?当前目录、上层目录用什么表示?主目录用什么表示? 切换目录用什么命…...

(13)Linux 进程的优先级、进程的切换以及环境变量等
前言:我们先讲解进程的优先级。然后讲解进程的切换,最后我们讲解环境变量,并且做一个 "让自己的可执行程序不带路径也能执行"的实践,讲解环境变量的到如何删除,最后再讲几个常见的环境变量。 一、进程优先级…...
C卷 (JavaPythonNode.jsC++))
数的分解(100%用例)C卷 (JavaPythonNode.jsC++)
给定一个正整数n,如果能够分解为m(m >1)个连续正整数之和,请输出所有分解中,m最小的分解。 如果给定整数无法分解为连续正整数,则输出字符串"N" 输入描述 输入数据为一整数,范围为 (1,2^30] 输出描述 比如输入为: 21 输出: 21=10+11 示例1 输入输出示例…...
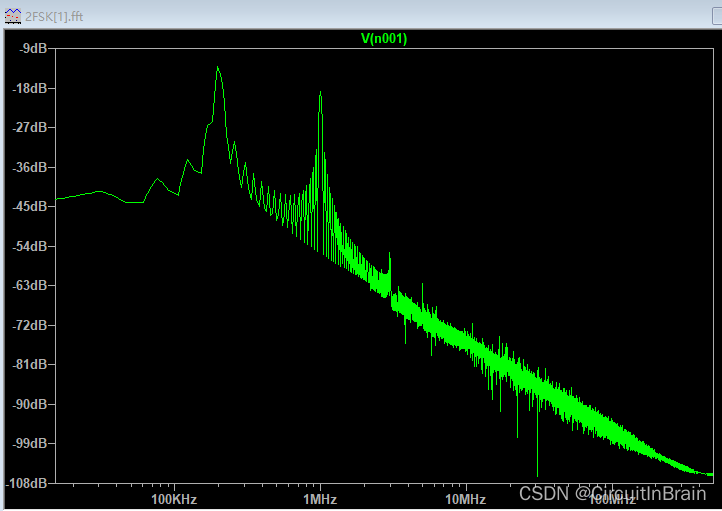
数字调制学习总结
调制:将基带的信号的频谱搬移到指定的信道通带内的过程。 解调:把指定信号通带内的信号还原为基带的过程。 1、2ASK调制 原理如下图所示,基带信号为单极不归零码,与载波信号相乘,得到调制信号。 调制电路可以用开关…...
AcWing 1129. 热浪(单源最短路)
题目链接 https://www.acwing.com/problem/content/1131/https://www.acwing.com/problem/content/1131/ 题解 此题属于单源最短路问题,根据数据范围,可以使用Dijkstra算法、堆优化版的Dijkstra算法、SPFA算法。本例采用SPFA算法,使用手写循…...
)
Mybatis Mapper XML文件-缓存(cache)
MyBatis包含一个强大的事务查询缓存特性,可以进行灵活的配置和自定义。在MyBatis 3的缓存实现中进行了许多改进,使其更加强大且更易于配置。 默认情况下,仅启用了本地会话缓存,该缓存仅用于缓存会话期间的数据。要启用全局的第二…...
电子科大软件系统架构设计——设计模式
设计模式概述 设计模式的背景 设计面向对象软件比较困难,而设计可以复用的面向对象软件更加困难不是解决任何问题都需要从头做起,最好能复用以往的设计方案经验面向对象软件设计经验需要有一定的模式记录下来,以提供给其他设计者使用&#…...

ubuntu20 安装缺失的字体
在/usr/share/fonts创建文件夹winfonts sudo mkdir winfonts 下载缺失的字体后,复制命令到对应的文件夹。 刷新字体库 sudo mkfontscale sudo mkfontdir sudo fc-cache...

2023年12月27日学习记录_加入噪声
目录 1、今日计划学习内容2、今日学习内容1、add noise to audio clipssignal to noise ratio(SNR)加入 additive white gaussian noise(AWGN)加入 real world noises 2、使用kaggel上的一个小demo:CNN模型运行时出现的问题调整采样率时出现bug 3、明确90dB下能否声…...

Java面试题86-95
86. Java代码查错(4)public class Something { public int addOne(final int x) { return x; }}此代码有错误吗?答案: 错。int x被修饰成final,意味着x不能在addOne method中被修改。87. Java代码查错(5&…...

看完谁再说搞不定上下角标?
一、需求 开发中有一些需要用到上下角标的地方,比如说化学式、数学式、注释。。。除了可以使用上下角标的标签,还可以通过css样式和CV大法实现,以下是具体实现方式。 二、实现方法 (1)标签写法: <sup…...

在 Python 中使用装饰器decorator的 7 个层次
在 Python 中使用装饰器的 7 个层次(7 Levels of Using Decorators in Python) 文章目录 在 Python 中使用装饰器的 7 个层次(7 Levels of Using Decorators in Python)导言Level 0: 了解基本概念Basic Concepts和用法Usages什么是装饰器decorator?我们为什么需要装…...

Vue.js项目部署至Linux服务器的详细步骤
引言 在现代Web开发中,Vue.js作为一款流行的前端框架,为开发者提供了灵活且高效的工具。然而,在将Vue.js项目成功部署到Linux服务器上,可能需要一些额外的步骤和注意事项。本文将深入介绍在Linux服务器上部署Vue.js项目的详细步骤…...

Java三层架构/耦合/IOC/DI
一.三层架构 controller/web 控制层。接收前端发送的请求,对请求进行处理,并响应数据。 service 业务逻辑层,处理具体的业务逻辑。 dao 数据访问层(Data Access Object),也称为持久层。负责数据访问操作,包括数据的增、…...

[调试]stm32使用过程debug记录,持续更新ing
遇到的bug:无法在串口助手接收到stm32向主机输出的数据,串口-USB RX灯不闪烁; 分析:闪烁灯实际上为一个二极管,CH 插入电脑USB接口时,RX处于高电平,当数据传输时,拉低电平导致其闪烁…...

知识付费小程序如何搭建?
随着互联网的发展和人们对知识的渴求,知识付费行业正逐渐崭露头角。而其中,知识付费小程序因其便捷性、个性化等特点,成为了越来越多人的首选。那么,如何搭建一个知识付费小程序呢?本文将为你揭秘从零到一的全过程&…...
springboot整合minio做文件存储
一,minio介绍 MinIO 是一个基于Apache License v2.0开源协议的对象存储服务。它兼容亚马逊S3云存储服务接口,非常适合于存储大容量非结构化的数据,例如图片、视频、日志文件、备份数据和容器/虚拟机镜像等,而一个对象文件可以是任意大小&…...

拥抱鸿蒙 - 在展讯T606平台上的探索与实践
前 言 自OpenHarmony 问世后受到了社会各界的广泛关注,OpenHarmony 的生态系统在如火如荼的发展。 酷派作为一家积极拥抱变化的公司,经过一段时间的探索与实践,成功实现将OpenHarmony 系统接入到展讯平台上,我们相信这是一个重要…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...
