白话机器学习的数学-1-回归
1、设置问题
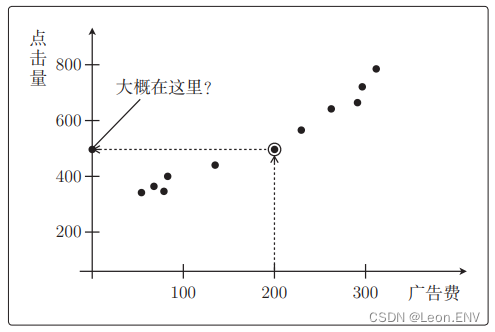
2、定义模型
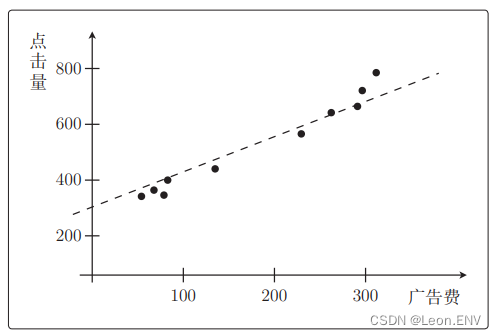
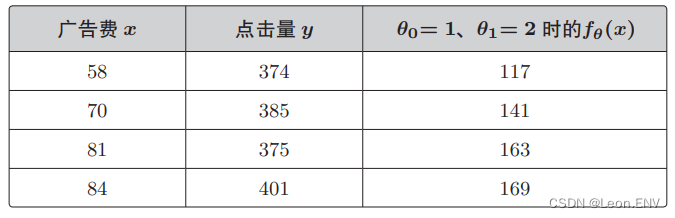
3、最小二乘法

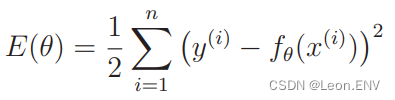
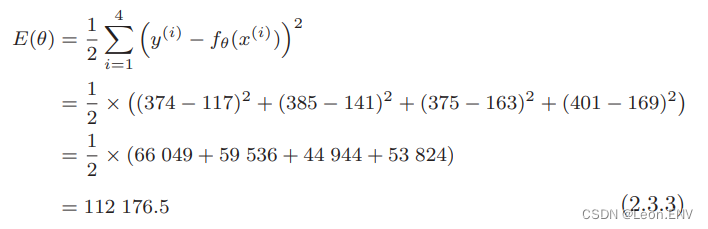
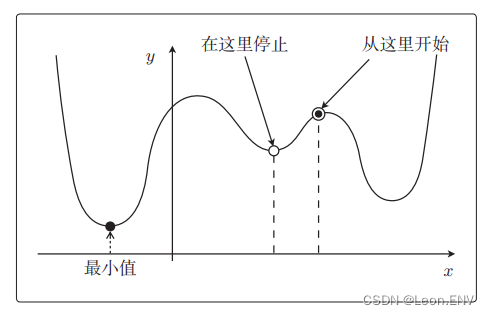
4、梯度下降法(最速下降法)
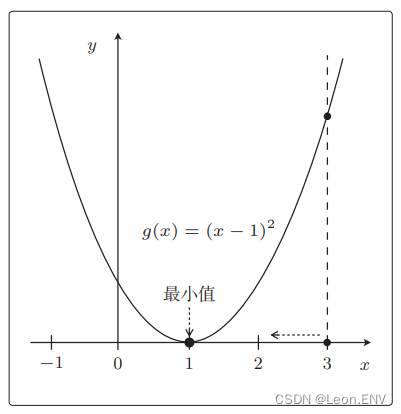
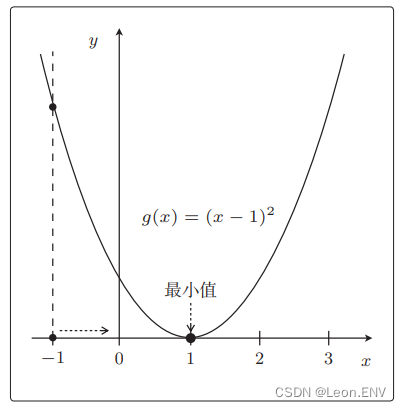
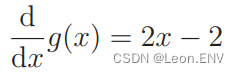
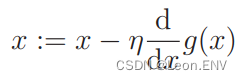
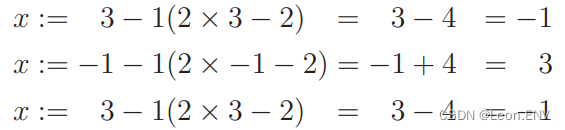
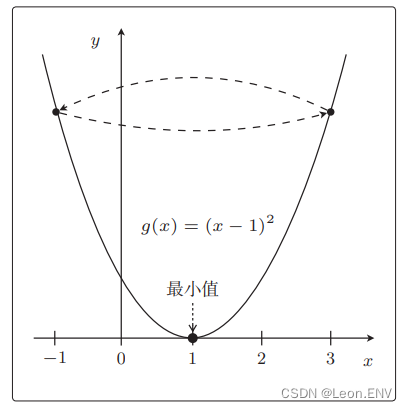
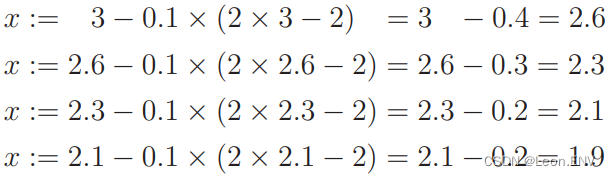
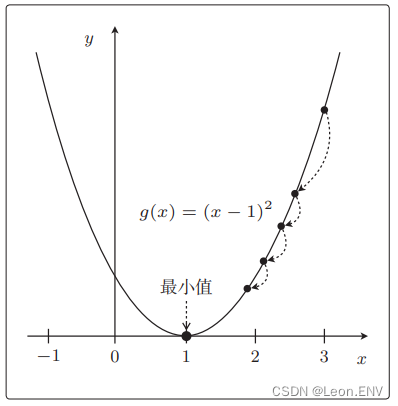
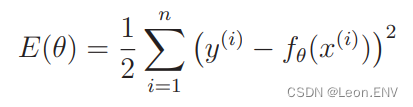
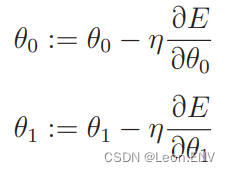

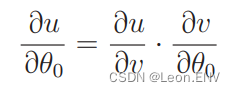
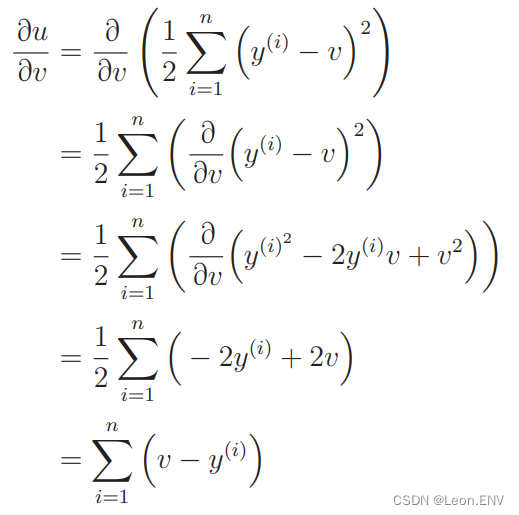
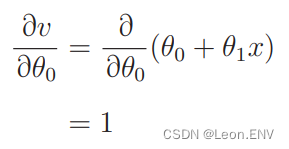

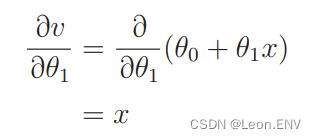
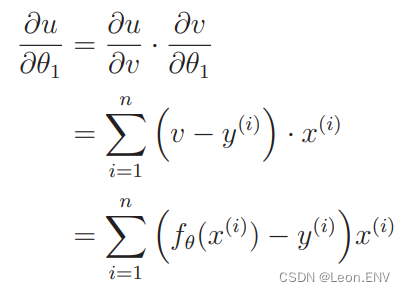

5、多项式回归
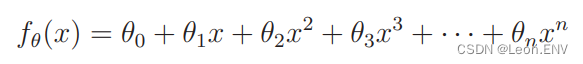
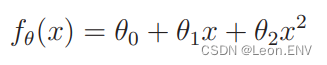

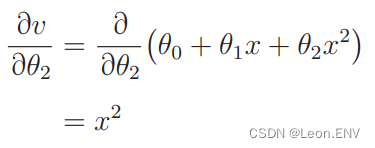
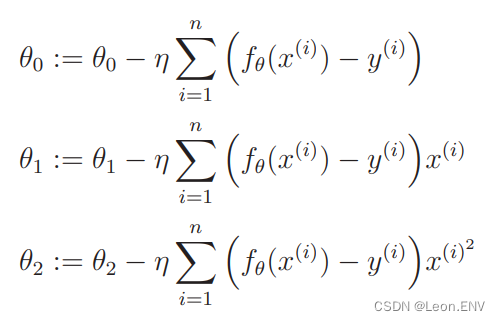
6、多重回归
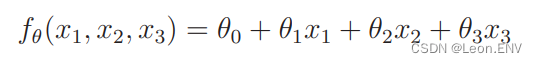
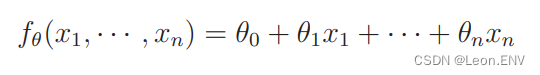
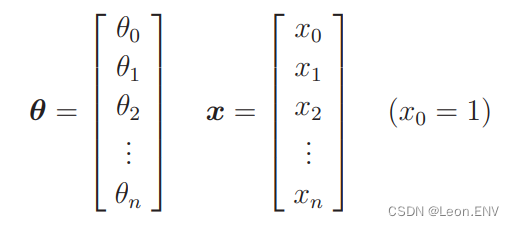
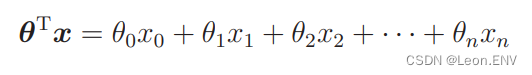
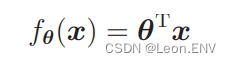
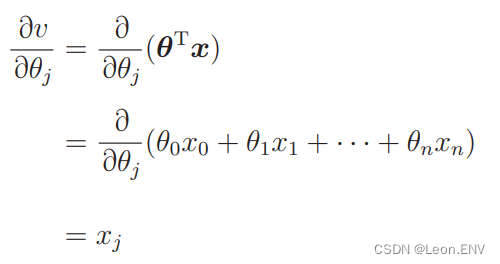
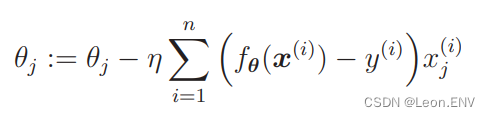
7、随机梯度下降法
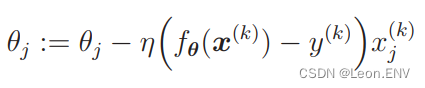
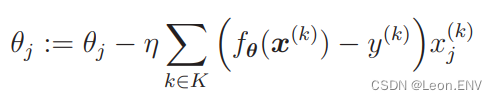
相关文章:
白话机器学习的数学-1-回归
1、设置问题 投入的广告费越多,广告的点击量就越高,进而带来访问数的增加。 2、定义模型 定义一个函数:一次函数 y ax b (a 是斜率、b 是截距) 定义函数: 3、最小二乘法 例子: 用随便确定的参…...
ubuntu22下安装minconda
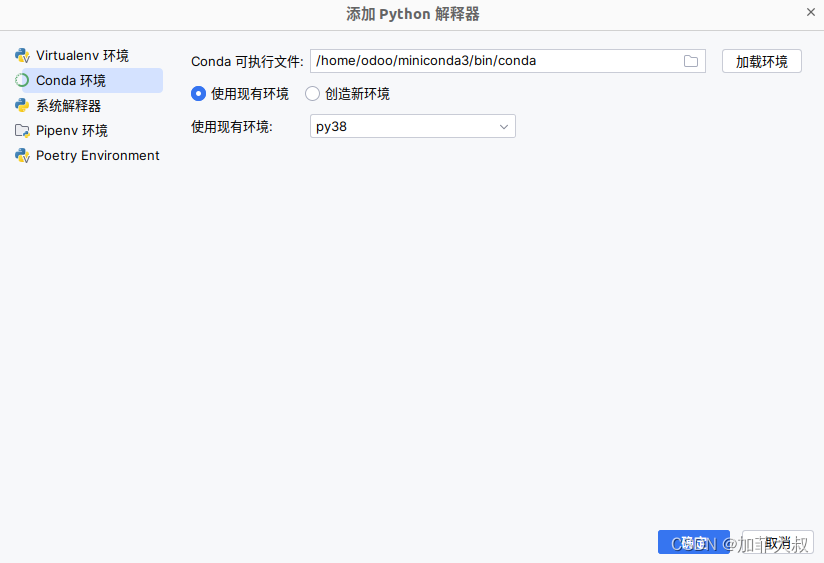
bing 搜索 canda install 找到官方网站 https://docs.conda.io/projects/miniconda/en/latest/ 这里我们安装minconda。 官网有安装方法。 mkdir -p ~/miniconda3 wget https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-x86_64.sh -O ~/miniconda3/miniconda.sh…...
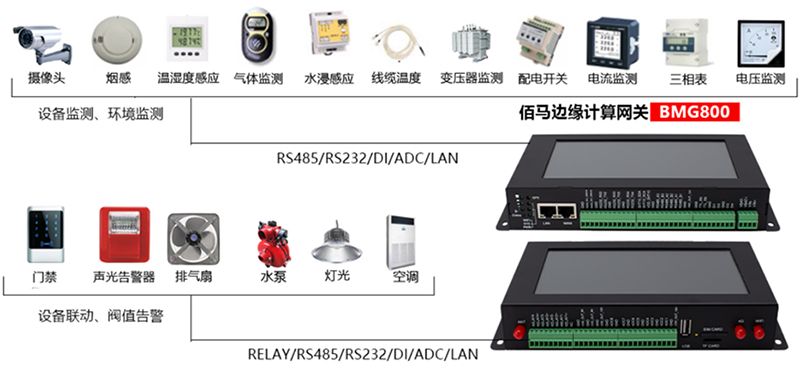
如何借助边缘网关打造智慧配电房安全方案
配电房是电力系统的重要组成部分,通常设置有各种高压配电装置和箱柜,是企业安全管理的重点。传统的人工巡检和监控总是难以避免疏漏,导致风险隐患的产生和扩大。 随着物联网、边缘计算、设备联动控制等技术的普及应用,佰马针对配电…...

k8s的二进制部署
k8s的二进制部署 k8s的二进制部署的实验: 源码包部署 k8s的master01:192.168.233.91 组件:kube-apiserver kube-controller-manager kube-scheduler etcd k8s的master02:192.168.233.92 组件:kube-api…...

Python基础语法总结
1.每条语句结束不需要分号(也可以加上), 直接换行, 注意: 如果两行代码写一行, 则必须加分号. 2.定义变量不需要指定类型(如果需要写类型, 需要在变量名后面加": 类型, 这个写法只是方便读代码). 3.变量名大小写敏感. 4.查看变量类型: type(变量名). 5.Python中的int表…...

矩阵理论基本知识
1、矩阵范数、算子范数 矩阵无穷范数是非自相容范数,矩阵1-范数、矩阵2-范数是自相容范数矩阵2-范数:Frobenius范数,是向量2-范数的自然推广。 ∥ A ∥ m 2 ∥ A ∥ F ∑ a i j ∗ a i j \|A\|_{m2}\|A\|_{F}\sqrt{\sum a_{ij}^*a_{ij}} ∥…...

《深入理解Java虚拟机(第三版)》读书笔记:Java内存区域与内存溢出异常、垃圾收集器与内存分配策略
下文是阅读《深入理解Java虚拟机(第3版)》这本书的读书笔记,如有侵权,请联系删除。 文章目录 第2章 Java内存区域与内存溢出异常2.2 运行时数据区域2.3 HotSpot虚拟机对象探秘 第3章 垃圾收集器与内存分配策略3.2 对象已死&…...

android 手机主界面侧滑退出app问题
最近重新搭了个app,发现手机显示APP主界面时,沿着手机右边向左滑,会直接关闭应用,所以想搞个第一次提示,第二次退出app的效果。 结果搞出个复杂的东西,下面是两段代码。1: 1:GestureDetector扩展函数。其…...

spring boot 配置全局日期和时间格式
spring boot 为项目配置 全局日期和时间格式化yyyy-MM-dd HH:mm:ss 方式一:代码配置全局日期和时间格式化 /*** author hua*/ Configuration public class WebConfiguration implements WebMvcConfigurer {/*** 项目全局时间格式化*/ Bean public ObjectMapper get…...
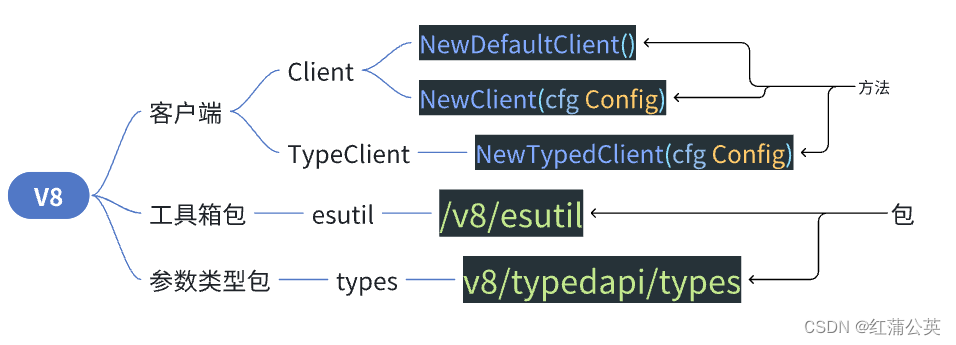
GoLang学习之路,对Elasticsearch的使用,一文足以(包括泛型使用思想)(二)
书写上回,上回讲到,Elasticsearch的使用前提即:语法,表结构,使用类型结构等。要学这个必须要看前面这个:GoLang学习之路,对Elasticsearch的使用,一文足以(包括泛型使用思…...
鸿蒙APP的代码规范
鸿蒙APP的代码规范是为了确保代码质量、可读性和可维护性而定义的一系列规则和标准。以下是一些建议的鸿蒙APP代码规范,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作。 1. 代码风格: 采用…...

蓝桥杯-每日刷题-027
出租汽车计费器 一、题目要求 题目描述 有一个城市出租汽车的计费规则是3公里内(含3公里)基本费6元,超过3公里,每一公里1.4元。 现在对于输入具体的公里数x(0<x<1000),编程计算x公里所需…...
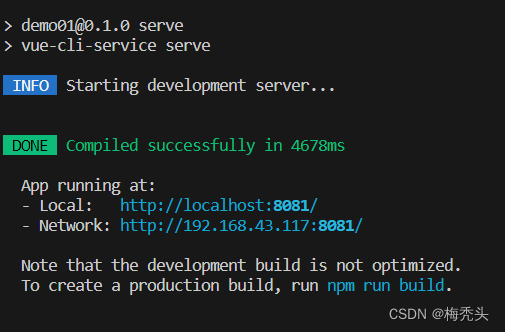
安装Node修改Node镜像地址搭建Vue脚手架创建Vue项目
1、安装VSCode和Node 下载VSCode Visual Studio Code - Code Editing. Redefined 下载Node Node.js (nodejs.org) 检验是否安装成功,WinR,输入cmd命令,使用node -v可以查看到其版本号 2、修改镜像地址 安装好node之后,开始修改镜像地址 …...

git 学习 之一个规范的 commit 如何写
最好的话做一件完整的事情就提交一次...

2023 年人工智能研究与技术排名前 10 的国家
人工智能研究是一项全球性的工作。虽然美国和中国因其对人工智能的贡献而备受关注,但事实是,世界各国都在涉足这项技术,尝试新的突破,并吸引投资者的关注。 斯坦福大学的《2023年人工智能报告》估计,到 2022 年&#…...
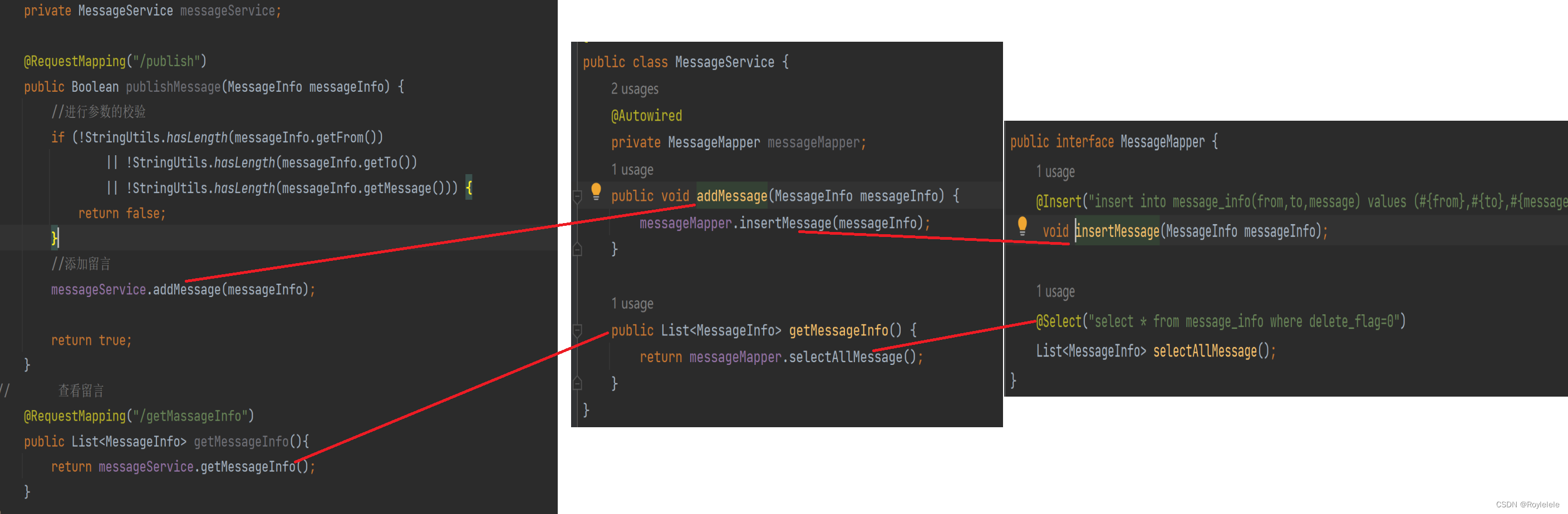
留言板(Mybatis连接数据库版)
目录 1.添加Mybatis和SQL的依赖 2.建立数据库和需要的表 3.对应表中的字段,补充Java对象 4.对代码进行逻辑分层 5.后端逻辑代码 之前的项目实例【基于Spring MVC的前后端交互案例及应用分层的实现】https://blog.csdn.net/weixin_67793092/article/details/134…...

第十二章 Sleuth分布式请求链路跟踪
Sleuth分布式请求链路跟踪 gitee:springcloud_study: springcloud:服务集群、注册中心、配置中心(热更新)、服务网关(校验、路由、负载均衡)、分布式缓存、分布式搜索、消息队列(异步通信)、数…...

EasyExcel多线程批量导出数据,动态表头,静态资源访问
1.导入依赖 <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.1.1</version></dependency>2.建立实体 Data public class ActResultLogVO implements Serializable {private static…...
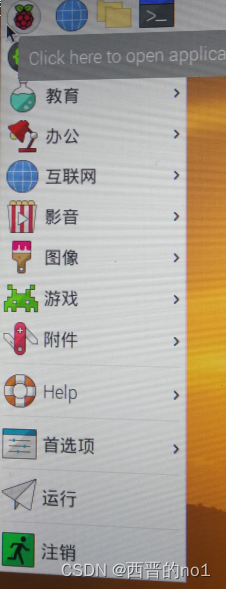
树莓派界面改成中文
安装完树莓派系统(Raspberry Pi OS with Desktop),第一次启动时,时会有如下面二个图所示,让你选择区域时区和语言。 树莓派默认的语言为英文,如果你在安装时没有选择的话,默认的区域为英国,语言为英国英文&…...
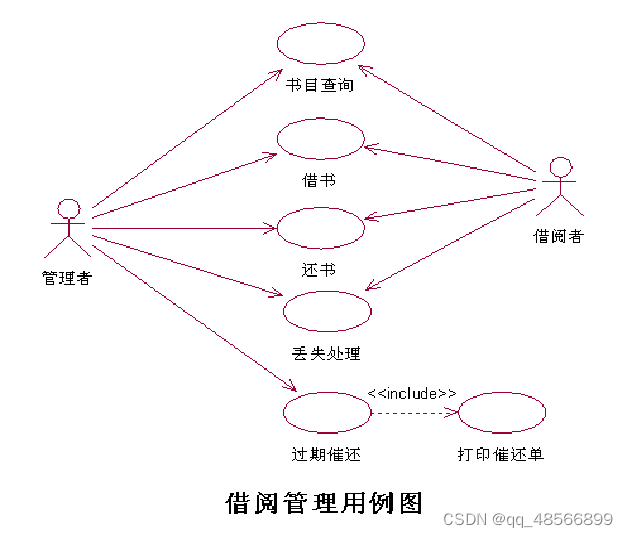
软件工程期末复习
● 用例:借书 ●参与者:管理员,借阅者 ●操作流: ① 管理员进入图书借阅界面,用例开始。 ② 系统要求输入借阅者的借书证编码。 ③系统检验借书证编码,如果正确,则显示借阅者的信息。 A1:借书证编码有错。 A2: 如果该借…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
