【计算机视觉】角点检测(Harris、SIFT)
Harris
角点指的是窗口延任意方向移动,都有很大变化量的点。
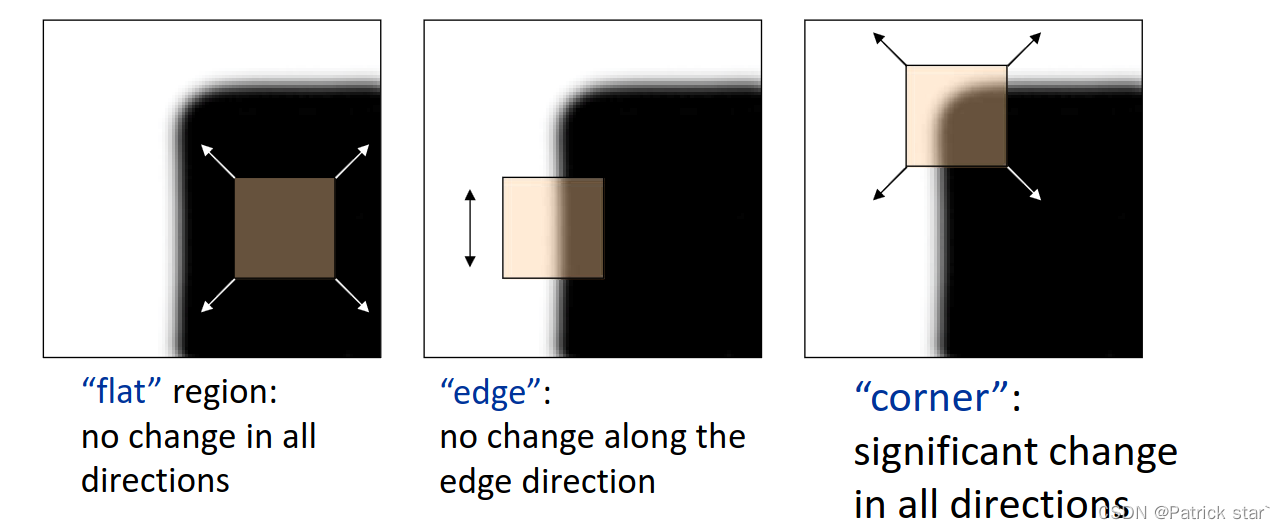
用数学公式表示为:
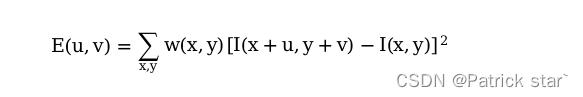
E(u,v)反映的移动后窗口的差异,w(x,y)为每个像素的点权值,I(x+u,y+v)是移动的像素值,I(x,y)是移动前的像素值。

将E(u,v)进行泰勒展开,直接建立E(u,v)和u,v的联系


最终:

M称为二阶矩矩阵(second moment matrix)
若 互不影响:
假设 :
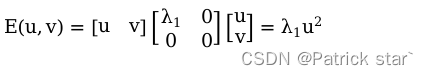
只有在u方向上变化是E才会变,因此只有 都不为0时(x,y)才是角点。
若 相关可以通过正交化变成前面的形式:
就反映了点在某个方向上的变化率,之后当
都很大时,该点才是角点。

为了减少计算可以用R来判定是否为角点
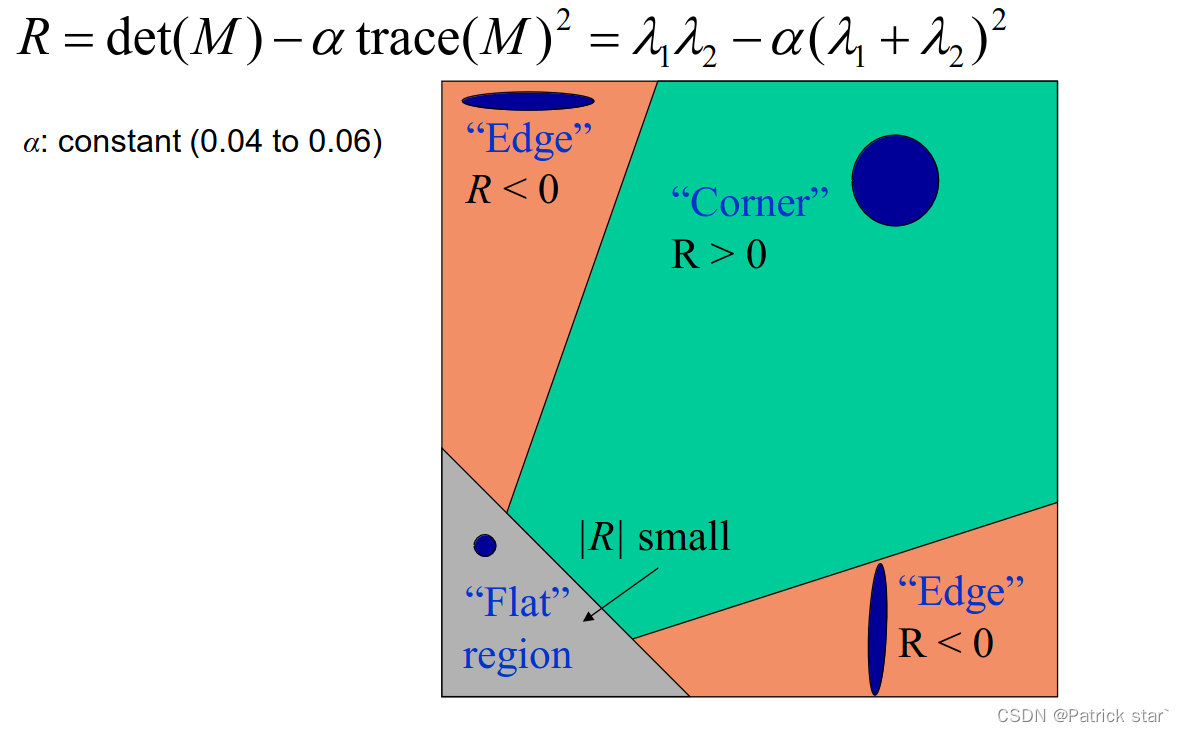
SIFT
Harris角点检测不具有尺度不变性,窗口大小不同,响应的结果也不同。

所谓的尺度不变性,指的是提取器能够对不同的尺度下的同一个点,有比较大的响应值。

接下来,介绍的SIFT就是具有尺度不变性的特征提取算法。
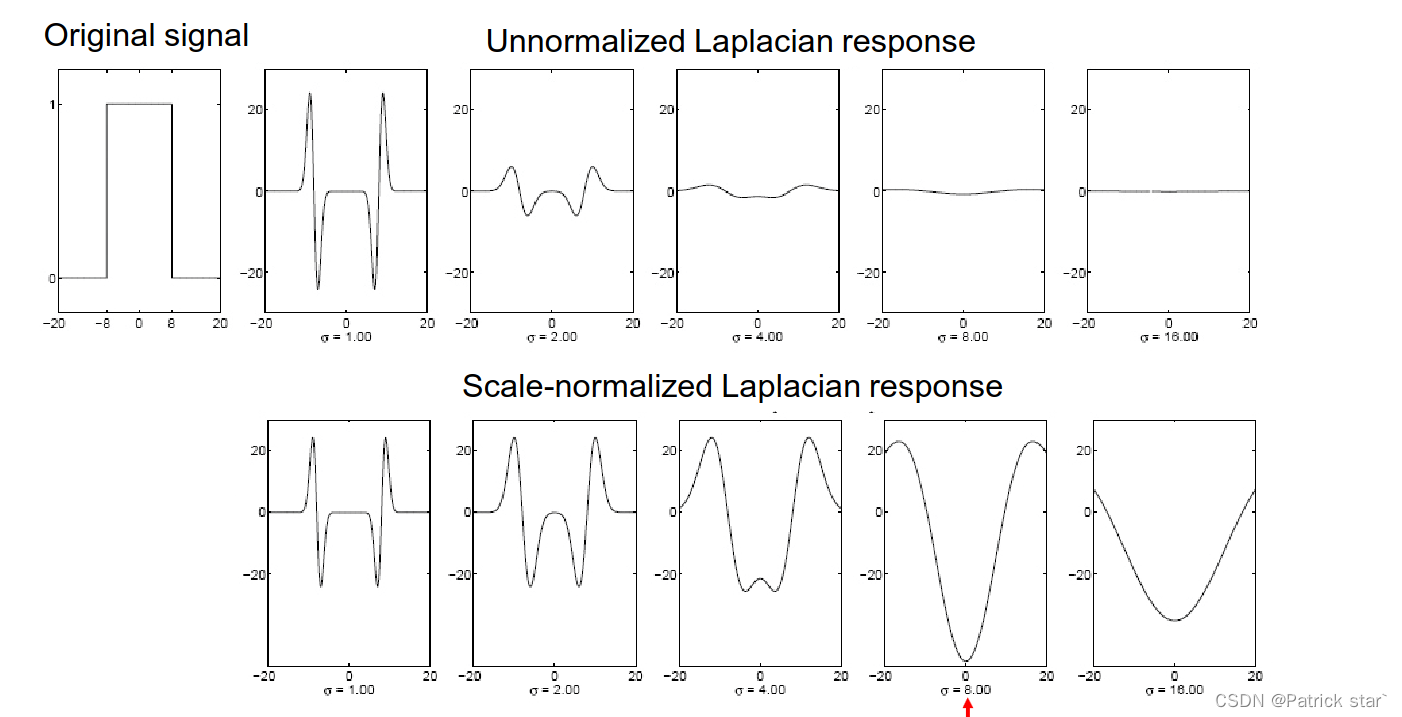
在边缘提取的时候,用高斯一阶导对信号进行卷积,响应值最大的就是边界。
如果用高斯二阶导对信号进行卷积,0点就是边界点(二阶导等于0的点,对应一阶导的极值点) 如果用高斯二阶导在不同的信号上进行卷积,当信号宽度与高斯滤波核匹配的时候,就能得到绝对值最大的信号,这样就建立了尺度和滤波核之间的联系。
如果用高斯二阶导在不同的信号上进行卷积,当信号宽度与高斯滤波核匹配的时候,就能得到绝对值最大的信号,这样就建立了尺度和滤波核之间的联系。
用不同的Laplacian对同一个信号进行卷积的时候,随着的增大,响应值会越来越不明显。

因为作为分母,
越来越大,卷积后的信号值就会越来越小 ,对于一阶偏导需要对卷积后的信号补偿
,对于二阶偏导需要对卷积后的信息补偿
,将响应值固定在一个尺度上。

补偿之后,就能用反映尺度
二维Laplacian高斯卷积核如下图所示:
当半径值正好与Laplacian为0的值匹配上的时候,响应值最大
假设这个圆是二进制的,简单来说就是找到一个合适的laplacian卷积核,卷积之后使得laplacian卷积核中小于0的部分权值为0,laplacian大于0的部分权值为1。
找到合适的laplacian卷积核,它的与信号半径有对应关系

SIFT使用的是DoG模版(两个高斯模版的差分),拥有和Laplacian类似的特性

一般而言,随着的增大,窗口也会变大,Laplacian每一次都会在原图进行卷积,卷积的成本就会增大。而DoG是利用高斯卷积核来做的,可以通过对较小
的卷积核卷积得到较大
的卷积核,减小卷积成本。


在找合适的尺度空间的时候,会进行非极大值抑制,只有当该点是27(上下两个尺度18个,当前尺度9个)个领接点中的极值时,认为该点为特征点,因此,有效DoG 个数为S时,总共的DoG个数为S+2(首尾不能构成三个尺度空间)。

每一个Octave表示对GuassianSpace缩小1/2后卷积,当我们需要更大的尺度的时候,需要跟大的sigma,意味着更大的卷积核更多的计算。SIFT算法中,将这样操作可以转换为,将图像缩小1/2,得到结果后将响应的sigma放大2倍,这样减少了计算的同时也得到了更大的尺度空间。

K的取值同样也很讲究, ,s为有效DoG个数。
K这样取值的好处是,对应高斯空间来说,只要将倒数第三图下采样2倍就能得到下一个Octave的第一个图,对于DoG空间来说,当前最后一个有效DoG的sigma与下一个Octave的第一个有效DoG的sigma是连续的(如图所示)

相关文章:

【计算机视觉】角点检测(Harris、SIFT)
Harris 角点指的是窗口延任意方向移动,都有很大变化量的点。 用数学公式表示为: E(u,v)反映的移动后窗口的差异,w(x,y)为每个像素的点权值,I(xu,yv)是移动的像素值,I(x,y)是移动前的像素值。 将E(u,v)进行泰勒展开&am…...

Python实现张万森下雪了的效果
系列文章 序号文章目录直达链接表白系列1浪漫520表白代码https://want595.blog.csdn.net/article/details/1306668812满屏表白代码https://want595.blog.csdn.net/article/details/1297945183跳动的爱心https://want595.blog.csdn.net/article/details/1295031234漂浮爱心http…...
C卷 (JavaPythonNode.jsC语言C++))
最长的指定瑕疵度的元音子串 (100%用例)C卷 (JavaPythonNode.jsC语言C++)
开头和结尾都是元音字母(aeiouAEIOU)的字符串为 元音字符串 ,其中混杂的非元音字母数量为其 瑕疵度 。比如 : “ a ” 、 “ aa ”是元音字符串,其瑕疵度都为 0 “ aiur ”不是元音字符串(结尾不是元音字符) “ abira ”是元音字符串,其瑕…...

Qt/C++音视频开发62-电子放大/按下选择区域放大显示/任意选取区域放大
一、前言 电子放大这个功能思考了很久,也是一直拖到近期才静下心来完整这个小功能,这个功能的前提,主要得益于之前把滤镜打通了,玩出花样来了,只要传入对应的滤镜字符串,就可以实现各种各样的效果…...

Vue(一):Vue 入门与 Vue 指令
Vue 01. Vue 快速上手 1.1 Vue 的基本概念 用于 构建用户界面 的 渐进性 框架 构建用户界面:基于数据去渲染用户看到的界面渐进式:不需要学习全部的语法就能完成一些功能,学习是循序渐进的框架:一套完整的项目解决方案&#x…...

C语言——最古老的树
归纳编程学习的感悟, 记录奋斗路上的点滴, 希望能帮到一样刻苦的你! 如有不足欢迎指正! 共同学习交流! 🌎欢迎各位→点赞 👍 收藏⭐ 留言📝 缺乏明确的目标,一生将庸庸…...

dnSpy调试工具断点信息是保存在哪里的呢
本人是C#开发,dnSpy工具用的比较多,有时候想把有用的断点信息保留下来,挪到别的机器上也能使用。我做这个事情的主要目标是在调试我们公司的程序时,顺带把访问的sql也进行输出,就可以偷懒不用每次都去查阅代码了&#…...

融汇贯通 —— 2023年技术与心灵的双重成长旅程
当我们站在2023年的岁末,回望这一年赋予我们的经历和挑战,心中涌动的感慨与启示像朝日初升的光芒,照亮脚下的路,亦照见心中的路。在此,我想分享几个方面的感悟和成长,愿它们能有所触动,成为您前…...
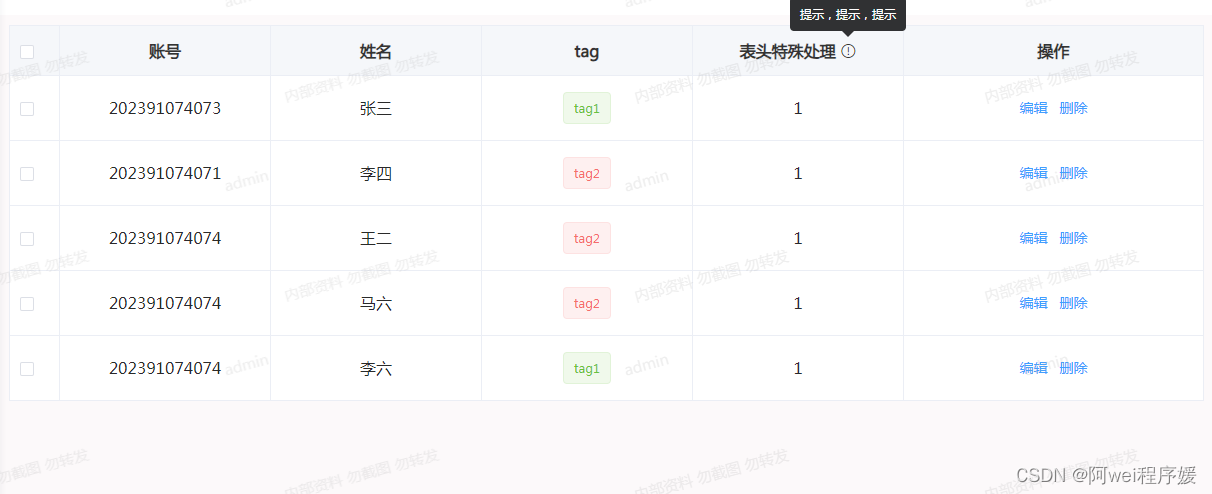
基于element ui封装table组件
效果图: 1.封装表格代码如下 <template> <div><div class"TableList"><el-tablev-loading"loading"selection-change"selectionChange"class"table":data"tableData":border"hasBorde…...
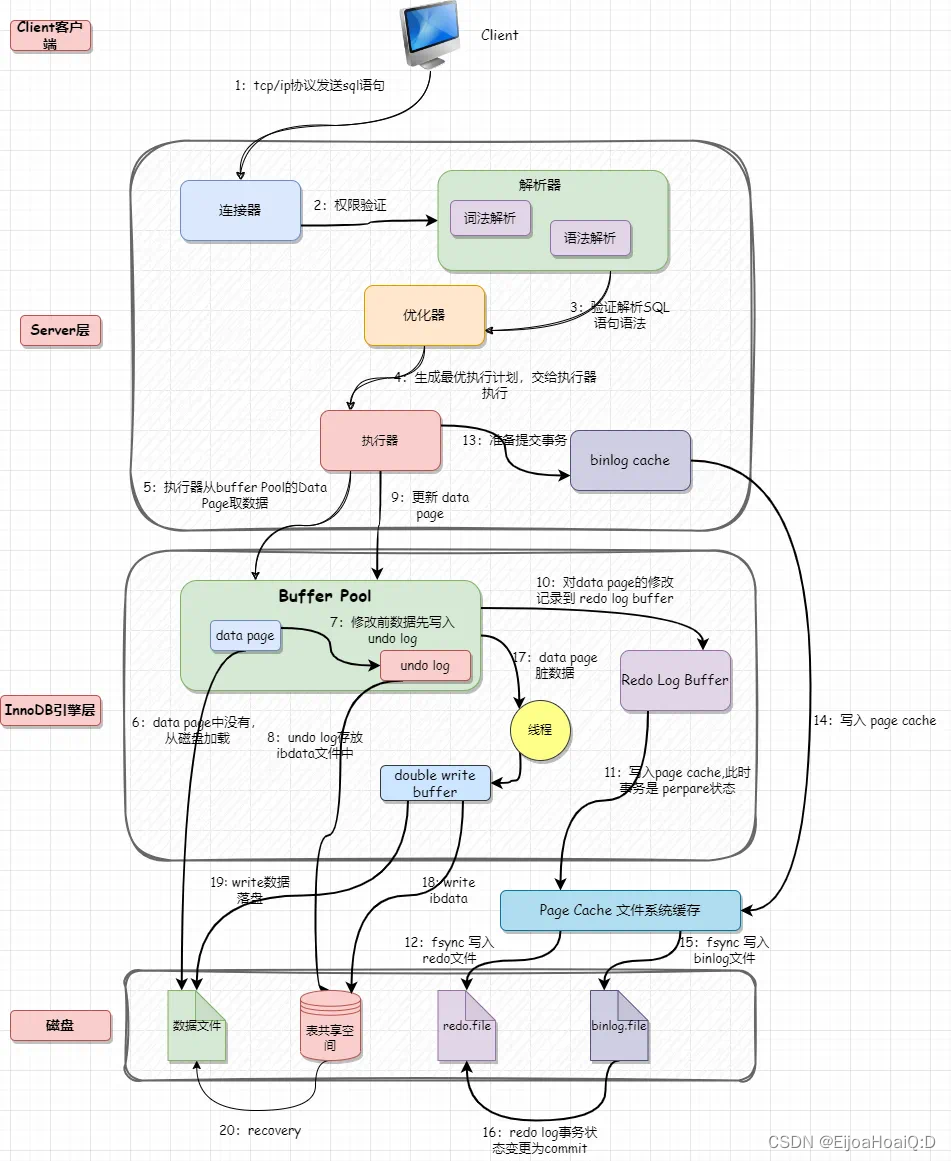
MySQL进阶之(一)逻辑架构
一、逻辑架构 1.1 逻辑架构剖析1.1.1 连接层1.1.2 服务层01、基础服务组件02、SQL Interface:SQL 接口03、Parser:解析器04、Optimizer:查询优化器05、Caches & Buffers: 查询缓存组件 1.1.3 引擎层1.1.4 存储层1.1.5 总结 1.…...
【前端学习指南】开启 Vue 的学习之旅
🍭 Hello,我是爱吃糖的范同学 秋招终于结束了(拿到了比较满意的 offer🎉🎉🎉,后续也会有“面筋”系类给大家分享),目前我终于也有足够的时间和精力来完成我 23 年遗留下…...

编程笔记 html5cssjs 011 HTML页面划分
编程笔记 html5&css&js 011 HTML页面划分 HTML的框架、区块和布局是什么,它们之前的关系是怎样的?框架注意 接下来要看一下网页内的划分。通过框架、区块及布局等方式,将网页从一个长方形整体划分为若干个部分,以合理展示…...
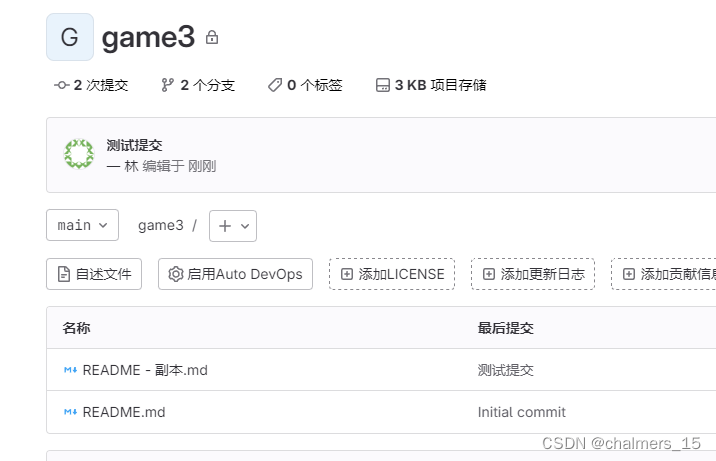
Centos7:Jenkins+gitlab+node项目启动(2)
Centos7:Jenkinsgitlabnode项目启动(1) Centos7:Jenkinsgitlabnode项目启动(1)-CSDN博客 Centos7:Jenkinsgitlabnode项目启动(2) Centos7:Jenkinsgitlabnode项目启动(2)-CSDN博客 Centos7:Jenkinsgitlabnode项目启…...
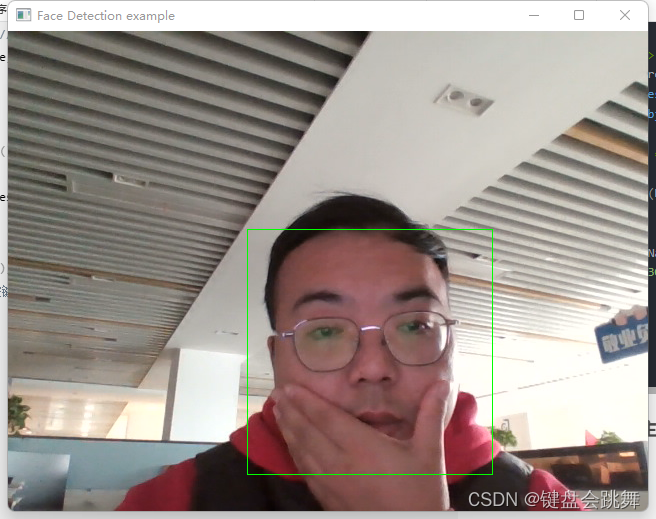
Qt+Opencv:人脸检测
话接上一篇,我们仍使用在上篇《QtOpencv:Qt中部署opencv》创建的Qt项目来测试opencv提供的sample。 在正式开始本篇之前,我们先说做一下准备工作: 一、opencv官方文档 学习最权威和最可靠的方式,就是阅读官方文档和…...
ChatGPT在地学、GIS、气象、农业、生态、环境等领域中的高级应用
以ChatGPT、LLaMA、Gemini、DALLE、Midjourney、Stable Diffusion、星火大模型、文心一言、千问为代表AI大语言模型带来了新一波人工智能浪潮,可以面向科研选题、思维导图、数据清洗、统计分析、高级编程、代码调试、算法学习、论文检索、写作、翻译、润色、文献辅助…...

Unreal Engine游戏引擎的优势
在现在这个繁荣的游戏开发行业中,选择合适的游戏引擎是非常重要的。其中,Unreal Engine作为一款功能强大的游戏引擎,在业界广受赞誉。那Unreal Engine游戏引擎究竟有哪些优势,带大家简单的了解一下。 图形渲染技术 Unreal Engin…...

[OCR]Python 3 下的文字识别CnOCR
目录 1 CnOCR 2 安装 3 实践 1 CnOCR CnOCR 是 Python 3 下的文字识别(Optical Character Recognition,简称OCR)工具包。 工具包支持简体中文、繁体中文(部分模型)、英文和数字的常见字符识别,支持竖…...
C卷 (JavaPythonNode.jsC语言C++))
字符串序列判定(100%用例)C卷 (JavaPythonNode.jsC语言C++)
输入两个字符串 S 和 L ,都只包含英文小写字母。 S 长度 <=100 , L 长度 <=500,000 。判定 S 是否是 L 的有效字串。 判定规则: S 中的每个字符在 L 中都能找到(可以不连续),且 S 在L中字符的前后顺序与 S 中顺序要保持一致。(例如, S="ace" 是 L=&q…...
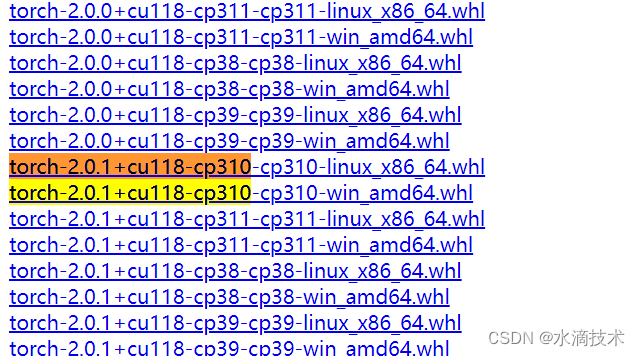
ERROR: No matching distribution found for torch==2.0.1解决方案
大家好,我是水滴~~ 本文主要介绍在安装 stable-diffusion-webui 时出现的 ERROR: No matching distribution found for torch2.0.1 问题的解决方案,希望能对你有所帮助。 《Python入门核心技术》专栏总目录・点这里 文章目录 问题描述解决方案离线安装 …...
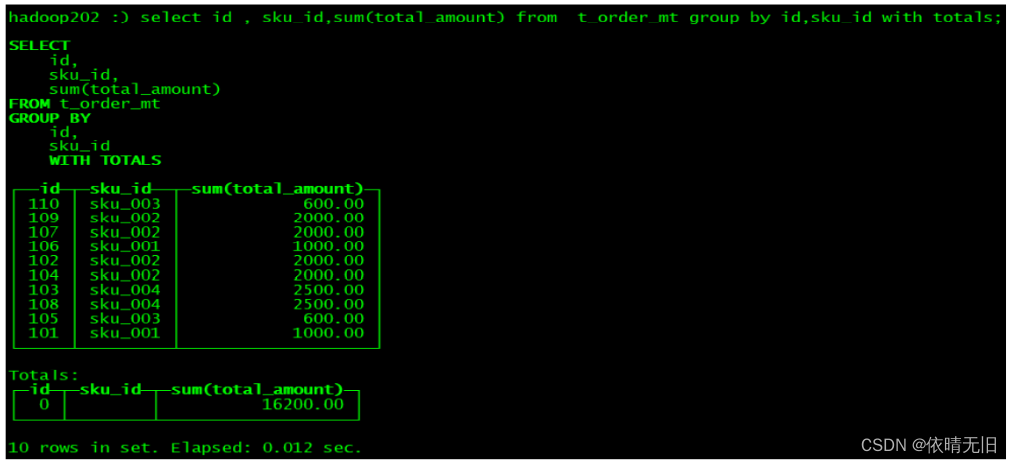
ClickHouse基础知识(五):ClickHouse的SQL 操作
基本上来说传统关系型数据库(以 MySQL 为例)的 SQL 语句,ClickHouse 基本都支持, 这里不会从头讲解 SQL 语法只介绍 ClickHouse 与标准 SQL(MySQL)不一致的地方。 1. Insert 基本与标准 SQL(My…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
