概率论相关题型
文章目录
- 概率论的基本概念
- 放杯子问题
- 条件概率与重要公式的结合
- 独立的运用
- 随机变量以及分布
- 离散随机变量的分布函数特点
- 连续随机变量的分布函数在某一点的值为0
- 正态分布标准化
- 随机变量函数的分布
- 多维随机变量以及分布
- 条件概率
- max 与 min 函数的相关计算
- 二维随机变量
- 二维随机变量求边缘概率密度
- 独立性
- Z = X + Y
- max{X,Y}
- 离散二维随机变量的条件概率以及max 与min
- 随机变量的数字特征
概率论的基本概念
- 1.互斥事件(互不相容)与对立事件:A 与 B 的交集为空集,A 和 B 不可能同时发生,区别于对立事件(在互斥事件的基础上,A 和 B 的和为全集)
- 对于互斥事件有 P(A + B + C ··· + Z) = P(A) + P(B) + P( C) + ··· + P(Z)
- 对于一般的不是互斥,
P(A+B) = P(A) + P(B ) - P(AB)这里不是P(A)*P(B),三个变量
P(A+B+C) = P(A) + P(B) + P© -P(AB) -P(AC) -P(BC) +P(ABC)- 古典概型,条件概率,三个重要的公式:乘法公式,全概率公式(化整为零),贝叶斯公式(利用先验概率求后验概率)
- 事件的独立性:P(AB) = P(A)P(B) ,三个事件的独立性要有四个式子成立------> n 各事件相互独立,则任意的2到n-1 的事件都相互独立,替换成对立事件也是成立的
- P(AB) = P(A) - P(AB非) 这个式子通过包含关系直接推出

为什么分母不使用12*11*10 ,分析,使用这个的话要注意 ,其实这个是A(3,10),那么就是讲究顺序的了,由于筛选是最终的结果,是不讲究顺序的,只能用C(3,10)
放杯子问题
- 将三个小球放进4各杯子,问杯中的最大小球个数分别为1,2,3的概率
站在小球的角度,选择杯子
- 对于1:那么就是432 / 444
- 对于3 :就是C(1,4) / 444
- 对于2: 就是1 - P(1) - P(3)
条件概率与重要公式的结合


可能一开始对于 求P(A2) 没有什么思路,搞不清楚应该怎么算,这时可以考虑用全概率公式

独立的运用

随机变量以及分布
- 注意区分离散型随机变量:二项分布,(0-1)分布,泊松分布,注意对它们分布列以及分布函数的求解(端点值?)
- 连续随机变量:均匀分布,指数分布,正态分布
- 指数分布是没有记忆性的P{X>s+t|X>s} = P{X>t}
- 二项分布的趋近为(np)泊松分布和正态分布
- 正态分布在u= 0 ,方差为1 时称为标准的正态分布

离散随机变量的分布函数特点


注意离散型随机变量的分布律与分布函数的关系
连续随机变量的分布函数在某一点的值为0

正态分布标准化

注意对带有绝对值的转换,以及带有负数的转换
随机变量函数的分布



对于函数是单调的话,可以使用公式法快速求解,如果不是单调的话,就按照定义一步步求解注意开始计算的时候,要提前确定好,Y 的范围,是否直接大于0,还是什么范围
多维随机变量以及分布
- 边缘分布:其中 Z = X + Y ,所得到的z 的边缘分布被称为卷积公式
- 对于 M =max{X,Y} 与 N = min{X,Y} 的分布函数的求法,其中X,Y 相互独立,且各自的分布函数Fx(x) 与 Fy(y) 那么有 F max(z) = Fx(x) * Fy(y) Fmin(z) = 1- (1-Fx(x))*(1-Fy(y))
对于上面的情况可以推广到 n 各相互独立的随机变量 ,都可以成立
最主要的是要分清,到底式子的形式是概率密度还是分布函数
条件概率

max 与 min 函数的相关计算

0.84 0.16
二维随机变量
对于开始的未知数的求解:分布函数的整体为1(1)对于X,Y 的确切的值的,就在相对应的面积范围内求解(2)对于边缘分布的,一方为给出的范围,另一方则为全部范围(3)像下面的第四题,其实的真正的目的,就是给x,y 一个更加具体的一个范围进行求解
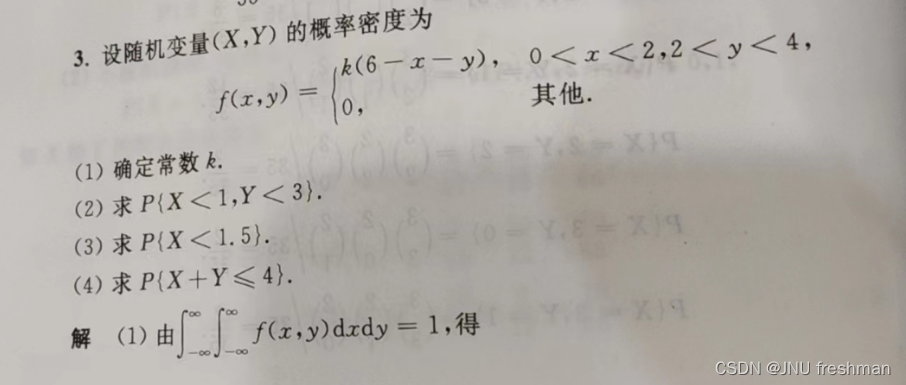

二维随机变量求边缘概率密度
以下面的第二问为例子:当你求x 的边缘概率密度时,你要把x 当作一个已经已知范围的一个常量,实际上y 才是你的变量,这就好比你其实是在求一条线(每当x 确定的时候),所以在求积分的上下限的时候,这时得到的应该是变量y 关于 x 的范围 , 也就是[x^2 , 1] ,当你求y 的概率密度的时候,y 就变成了常量,积分的上下限应该是变量x 关于常量 y 的一个范围,也就是[ - 根号 y, 根号y ]

独立性
对于独立性的证明,就按照定义来即可,分布函数或者概率密度都可以


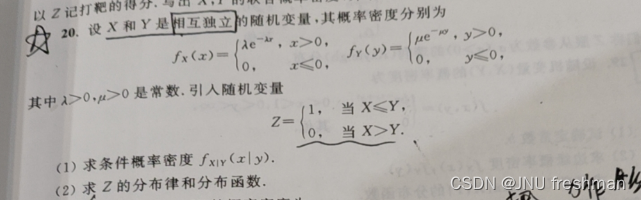

简单的分析:由一开始的独立性,得出f(x,y),对于后面的z ,其实 z 的取值范围已经给出,所谓的求分布律就是让你求相对应的概率,这个概率也就是f(x,y) 相对应的概率
Z = X + Y
卷积的两种方法都是等价的,不过下面的第一种方法相对来说更加简单,计算以及运算的过程在于你的选择利用公式来求,同样地,与求边缘概率密度一样,这里将z 看成常量,x 和 y 是看成以 z 为变量的一个函数,有时候是要进行分段进行一个计算并不建议一个大括号直接运算完成,而是以z 的范围作为分隔,一个个进行计算
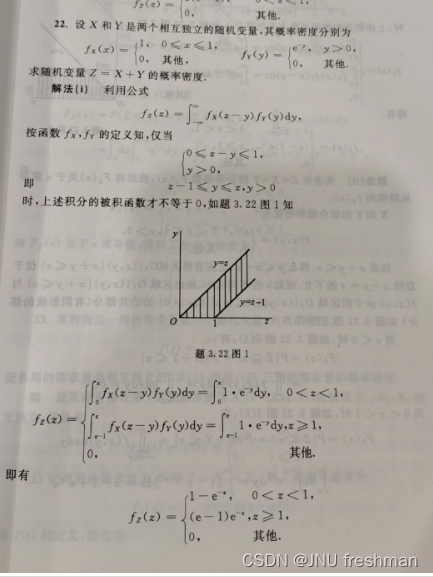
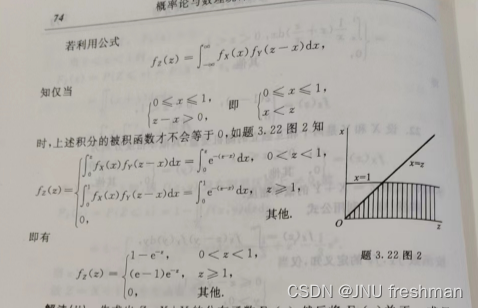
max{X,Y}
注意最后的时候的变量都替换成u 了

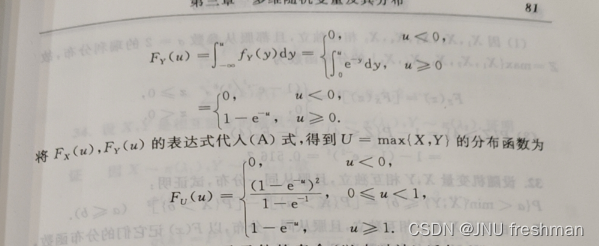
离散二维随机变量的条件概率以及max 与min
在离散随机变量中,条件概率的理解 p{X = 2| Y = 2} 由于是在Y = 2 的条件下,那么就要将Y = 2 的全部情况算进去(不止一个x) ,但是X = 2 的话,就只是一个x ,同理是可以类推到连续的随机变量的
对于离散型的max 与min 的话,不如直接列举进行一个计算,连续型才用公式
随机变量的数字特征
- (1) 懂得离散型随机变量与连续型随机变量的期望的求法
- (2)随机变量的函数的数学期望:对于离散型,直接将每个取值代入函数,得到新的取值,再和相对应的概率相乘再相加即可;对于连续型随机变量,直接对g(x)f(x) 进行积分 ,(区别于f(x) 自身的期望, xf(x) 的积分
- (3)对于二维的随机变量:对于离散型,就是相对应的取值乘概率后相加;对于连续型就变成 对g(x,y)f(x,y) 的一个求积分的过程
- (4) 注意期望的相关计算的公式:E(x+y) = E(x) + E(y) (减号也是一样) E(XY) = E(X)E(Y) 当X,Y 相互独立的时候成立 (这两个公式均可以推广)
- (5)方差 D(x) = E{[X-E(X)]^2} ,就是每一个取值与期望的差的平方的期望,它的算数平方根为均方差
当计算离散随机变量的时候,[X-E(X)]^2 乘相对应的概率再求和即可; 连续型的时候 [X-E(X)] ^2 乘f(x) 的积分由于计算方差难度问题,常常用 D(X) = E(X^2) - [E(X)]^2 来计算- 方差的相关性质:常数的方差为0, D(cX) = c^2 D(X) D(C+ X) = D(X)
D(X+Y ) = D(X) + D(Y) + 2E{(X-E(x))(Y-E(y))}
D(X-Y ) = D(X) + D(Y) - 2E{(X-E(x))(Y-E(y))}
当X ,Y 相互独立的时候,D(X+Y) = D(X-Y) = D(X) + D(Y)- 标准化的随机变量,就是 X- E(X) / 均方差
- 协方差 Cov(X,Y) = E{(X-E(x))(Y-E(y))} 相关系数 = Cov(X,Y) /X 的均方差乘Y的均方差
- 协方差可以写成 Cov(X,Y) = E(XY) - E(X)E(Y)
- 协方差的相关性质 Cov(aX,bY) = abCov(X,Y) Cov(X1+X2,Y) = Cov(X1,Y) + Cov(X2+Y)
相关系数 = 0 时,称为X 与 Y 不相关(就是X 与 Y 没有线性关系,但是可能会存在其他的关系)相互独立可以推出不相关,但是不相关推不出相互独立, 不相关 与 相关系数 = 0,Cov(X,Y) =0 E(XY) = E(X)E(Y)对于二维正态随机变量的相互独立与不相关的条件是相互等价的
- 矩、协方差矩:分清k 阶原点矩,k 阶中心距,k+l 阶混合矩 k + l 阶混合中心矩

切比雪夫不等式给出了再随机变量X 的分布未知,只知道E(X) 与D(X) 的情况下,对E{|X-E(X)|<=m} 概率的下限的估计
相关文章:

概率论相关题型
文章目录 概率论的基本概念放杯子问题条件概率与重要公式的结合独立的运用 随机变量以及分布离散随机变量的分布函数特点连续随机变量的分布函数在某一点的值为0正态分布标准化随机变量函数的分布 多维随机变量以及分布条件概率max 与 min 函数的相关计算二维随机变量二维随机变…...

C#中的Attribute详解(上)
C#中的Attribute详解(上) 一、Attribute是什么二、Attribute的作用三、Attribute与注释的区别四、系统Attribute范例1、如果不使用Attribute,为了区分这四类静态方法,我们只能通过注释来说明,但这样做会给系统带来很多…...

天津医科大学临床医学院专升本药学专业有机化学考试大纲
天津医科大学临床医学院高职升本科专业课考试大纲药学专业《有机化学》科目考试大纲 一、考试基本要求 本考试大纲主要要求考生对《有机化学》基本概念有较深入的了解,能够系统地掌握各类化合物的命名、结构特点及立体异构、主要性质、反应、来源和合成制备方法等…...
电脑开机自动断电,简单4招,快速解决!
“不知道我的电脑最近是怎么回事,每次一开机就会出现自动断电的情况,有什么方法可以解决吗?” 在使用电脑时,由于电源供应不稳定或过热,以及各种硬件问题,可能会导致电脑开机自动断电。遇到这种情况&#x…...
线程基础知识(三)
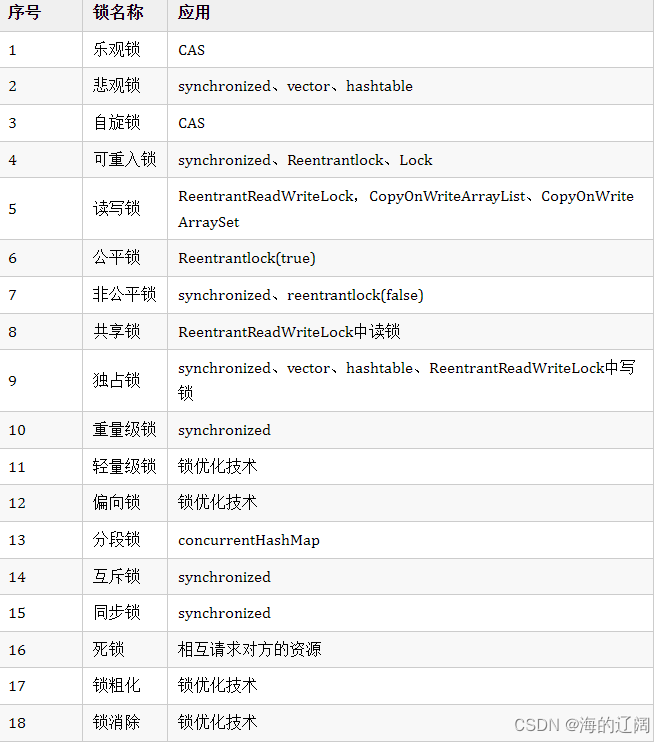
前言 之前两篇文章介绍了线程的基本概念和锁的基本知识,本文主要是学习同步机制,包括使用synchronized关键字、ReentrantLock等,了解锁的种类,死锁、竞争条件等并发编程中常见的问题。 一、关键字synchronized synchronied关键…...

elasticsearch系列七:聚合查询
概述 今天咱们来看下es中的聚合查询,在es中聚合查询分为三大类bucket、metrics、pipeline,每一大类下又有十几种小类,咱们各举例集中,有兴许的同学可以参考官网:https://www.elastic.co/guide/en/elasticsearch/refere…...

SQL面试题挑战11:访问会话切割
目录 问题:SQL解答: 问题: 如下为某电商公司用户访问网站的数据,包括用户id和访问时间两个字段。现有如下规则:如果某个用户的连续的访问记录时间间隔小于60秒,则属于同一个会话,现在需要计算每…...
)
2023“楚怡杯”湖南省赛“信息安全管理与评估“--应急响应(高职组)
2023“楚怡杯”湖南省“信息安全管理与评估”(高职组)任务书 2023“楚怡杯”湖南省“信息安全管理与评估”(高职组)任务书第一阶段竞赛项目试题第二阶段竞赛项目试题网络安全事件响应:需要环境私聊博主:2023“楚怡杯”湖南省“信息安全管理与评估”(高职组)任务书 第一…...

【Python百宝箱】Python引领制造变革:CAM技术全景解析与实战指南
Python 驭技术潮流:探索计算机辅助制造的全方位工具库 前言 在当今制造业的快速发展中,计算机辅助制造(Computer-Aided Manufacturing,CAM)技术扮演着至关重要的角色。为了提高制造效率、优化工艺流程以及实现数字化…...

【新版Hi3559AV100 旗舰8K30 AI摄像机芯片】
新版Hi3559AV100 旗舰8K30 AI摄像机芯片 一、总体介绍 Hi3559AV100是专业的8K Ultra-HD Camera SOC,它提供了8K30/4K120广播级图像质量的数字视频录制,支持8路Sensor输入,支持H.265编码输出或影视级的RAW数据输出,并集成高性能ISP…...
)
小样本学习idea(不断更新)
在此整理并记录自己的思考过程,其中不乏有一些尚未成熟或者尚未实现的idea,也有一些idea实现之后没有效果或者正在实现,当然也有部分idea已写成论文正在投稿,都是自己的一些碎碎念念的思考,欢迎交流。 研一上学期 9.…...
表情包搜索网站
一个非常不错的表情包搜索网站,输入关键词即可得到所有相关的表情,还可以选择套图下载,自制表情,非常给力666 可以点击下载,会新建窗口打开图片,鼠标右键“图片另存为”,下载文件名手动补充“…...
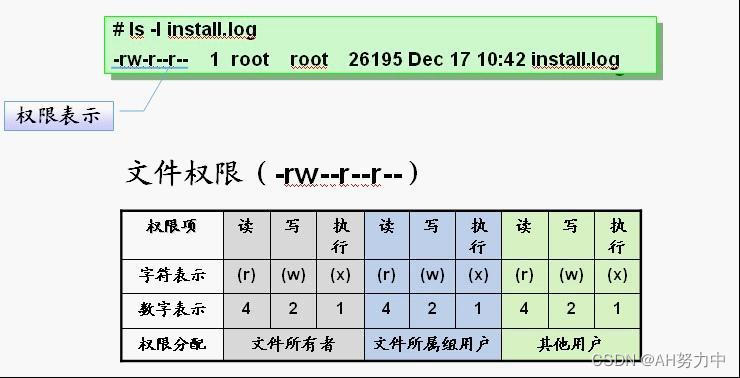
Linux账号和权限管理
目录 一、用户账号和组账号概述 1、用户账号类型 2、组账号 1.基本组(私有组) 2.附加组(公共组) 3、ID 1.UID 2.GID 4、用户和账号管理 1.文件位置 2.useradd-----创建用户 3.userdel——删除用户账号 4.usermod---修…...
)
Qt/QML编程学习之心得:QML和C++的相互调用(十五)
Qt下的QML说到底是类似于JavaScript的一种解释性语言,习惯了VC的MVC(Veiw+Control)的模式,那种界面视图任何事件都是和C++的cpp中处理函数一一对应,在类中也有明确的说明的。一下子玩Qt会觉得哪里对不上,比如使用QML这种节脚本语言贴了图做了layout布局,那么一个按钮的o…...
月入10.5K,专科小伙转行网优:据说每个领域都有一个“显眼包”
网络热词流行的今天,显眼包一词又上热搜。除了熟知的内娱显眼包外,其实各行业也都有自己的“显眼包”。 显眼包又叫“现眼包”看似丢人现眼,实则是个“褒义词”,他们勇敢自信,积极乐观,敢于展示自己&#x…...

Python自动化测试:选择最佳的自动化测试框架
在开始学习python自动化测试之前,先了解目前市场上的自动化测试框架有哪些? 随着技术的不断迭代更新,优胜劣汰也同样发展下来。从一开始工具型自动化,到现在的框架型;从一开始的能用,到现在的不仅能用&…...
Ubuntu16.04 安装Anaconda
步骤 1: 去官网下载安装包,链接如下: https://repo.anaconda.com/archive/ 找到对应版本下载至本地电脑,并上传至服务器。 步骤2: 通过命令解压 sh Anaconda3-2023.03-0-Linux-x86_64.sh 一路选择yes或则回车,直到安装成功出现下面画面&…...
MR实战:统计总分与平均分
文章目录 一、实战概述二、提出任务三、完成任务(一)准备数据1、在虚拟机上创建文本文件2、上传文件到HDFS指定目录 (二)实现步骤1、创建Maven项目2、添加相关依赖3、创建日志属性文件4、创建成绩映射器类5、创建成绩驱动器类6、启…...
Redux与React环境准备、实现counter(及传参)、异步获取数据
环境说明: 一:说明 在React中使用redux,官方要求安装两个其他插件:Redux Toolkit和react-redux 1. Redux ToolKit(RTK) - 官方推荐编写Redux逻辑的方式,是一套工具的集合集,简化书写方式 (简化…...
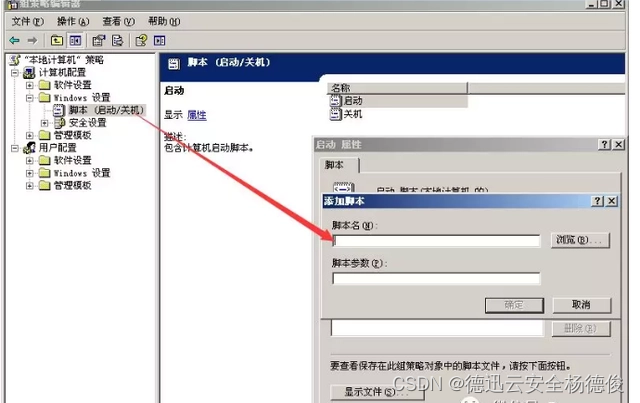
网站服务器被入侵,如何排查,该如何预防入侵呢?
在我们日常使用服务器的过程中,当公司的网站服务器被黑客入侵时,导致整个网站以及业务系统瘫痪,将会给企业带来无法估量的损失。作为服务器的维护人员应当在第一时间做好安全响应,对入侵问题做到及时处理,以最快的时间…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...



