【机器学习】【线性回归】梯度下降
文章目录
- @[toc]
- 数据集
- 实际值
- 估计值
- 估计误差
- 代价函数
- 学习率
- 参数更新
- `Python`实现
- 导包
- 数据预处理
- 迭代过程
- 数据可视化
- 完整代码
- 线性拟合结果
- 代价结果
文章目录
- @[toc]
- 数据集
- 实际值
- 估计值
- 估计误差
- 代价函数
- 学习率
- 参数更新
- `Python`实现
- 导包
- 数据预处理
- 迭代过程
- 数据可视化
- 完整代码
- 线性拟合结果
- 代价结果

个人主页:丷从心
系列专栏:机器学习

数据集
( x ( i ) , y ( i ) ) , i = 1 , 2 , ⋯ , m \left(x^{(i)} , y^{(i)}\right) , i = 1 , 2 , \cdots , m (x(i),y(i)),i=1,2,⋯,m
实际值
y ( i ) y^{(i)} y(i)
估计值
h θ ( x ( i ) ) = θ 0 + θ 1 x ( i ) h_{\theta}\left(x^{(i)}\right) = \theta_{0} + \theta_{1} x^{(i)} hθ(x(i))=θ0+θ1x(i)
估计误差
h θ ( x ( i ) ) − y ( i ) h_{\theta}\left(x^{(i)}\right) - y^{(i)} hθ(x(i))−y(i)
代价函数
J ( θ ) = J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 = 1 2 m ∑ i = 1 m ( θ 0 + θ 1 x ( i ) − y ( i ) ) 2 J(\theta) = J(\theta_{0} , \theta_{1}) = \cfrac{1}{2m} \displaystyle\sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right)^{2}} = \cfrac{1}{2m} \displaystyle\sum\limits_{i = 1}^{m}{\left(\theta_{0} + \theta_{1} x^{(i)} - y^{(i)}\right)^{2}} J(θ)=J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2=2m1i=1∑m(θ0+θ1x(i)−y(i))2
学习率
- α \alpha α是学习率,一个大于 0 0 0的很小的经验值,决定代价函数下降的程度
参数更新
Δ θ j = ∂ ∂ θ j J ( θ 0 , θ 1 ) \Delta{\theta_{j}} = \cfrac{\partial}{\partial{\theta_{j}}} J(\theta_{0} , \theta_{1}) Δθj=∂θj∂J(θ0,θ1)
θ j : = θ j − α Δ θ j = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_{j} := \theta_{j} - \alpha \Delta{\theta_{j}} = \theta_{j} - \alpha \cfrac{\partial}{\partial{\theta_{j}}} J(\theta_{0} , \theta_{1}) θj:=θj−αΔθj=θj−α∂θj∂J(θ0,θ1)
[ θ 0 θ 1 ] : = [ θ 0 θ 1 ] − α [ ∂ J ( θ 0 , θ 1 ) ∂ θ 0 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ] \left[ \begin{matrix} \theta_{0} \\ \theta_{1} \end{matrix} \right] := \left[ \begin{matrix} \theta_{0} \\ \theta_{1} \end{matrix} \right] - \alpha \left[ \begin{matrix} \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{0}}} \\ \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{1}}} \end{matrix} \right] [θ0θ1]:=[θ0θ1]−α ∂θ0∂J(θ0,θ1)∂θ1∂J(θ0,θ1)
[ ∂ J ( θ 0 , θ 1 ) ∂ θ 0 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ] = [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) ] = [ 1 m ∑ i = 1 m e ( i ) 1 m ∑ i = 1 m e ( i ) x ( i ) ] e ( i ) = h θ ( x ( i ) ) − y ( i ) \left[ \begin{matrix} \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{0}}} \\ \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{1}}} \end{matrix} \right] = \left[ \begin{matrix} \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right)} \\ \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{\left(h_{\theta}\left(x^{(i)}\right) - y^{(i)}\right) x^{(i)}} \end{matrix} \right] = \left[ \begin{matrix} \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)}} \\ \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)} x^{(i)}} \end{matrix} \right] \kern{2em} e^{(i)} = h_{\theta}\left(x^{(i)}\right) - y^{(i)} ∂θ0∂J(θ0,θ1)∂θ1∂J(θ0,θ1) = m1i=1∑m(hθ(x(i))−y(i))m1i=1∑m(hθ(x(i))−y(i))x(i) = m1i=1∑me(i)m1i=1∑me(i)x(i) e(i)=hθ(x(i))−y(i)
[ ∂ J ( θ 0 , θ 1 ) ∂ θ 0 ∂ J ( θ 0 , θ 1 ) ∂ θ 1 ] = [ 1 m ∑ i = 1 m e ( i ) 1 m ∑ i = 1 m e ( i ) x ( i ) ] = [ 1 m ( e ( 1 ) + e ( 2 ) + ⋯ + e ( m ) ) 1 m ( e ( 1 ) + e ( 2 ) + ⋯ + e ( m ) ) x ( i ) ] = 1 m [ 1 1 ⋯ 1 x ( 1 ) x ( 2 ) ⋯ x ( m ) ] [ e ( 1 ) e ( 2 ) ⋮ e ( m ) ] = 1 m X T e = 1 m X T ( X θ − y ) \begin{aligned} \left[ \begin{matrix} \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{0}}} \\ \cfrac{\partial{J(\theta_{0} , \theta_{1})}}{\partial{\theta_{1}}} \end{matrix} \right] &= \left[ \begin{matrix} \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)}} \\ \cfrac{1}{m} \displaystyle\sum\limits_{i = 1}^{m}{e^{(i)} x^{(i)}} \end{matrix} \right] = \left[ \begin{matrix} \cfrac{1}{m} \left(e^{(1)} + e^{(2)} + \cdots + e^{(m)}\right) \\ \cfrac{1}{m} \left(e^{(1)} + e^{(2)} + \cdots + e^{(m)}\right) x^{(i)} \end{matrix} \right] \\ &= \cfrac{1}{m} \left[ \begin{matrix} 1 & 1 & \cdots & 1 \\ x^{(1)} & x^{(2)} & \cdots & x^{(m)} \end{matrix} \right] \left[ \begin{matrix} e^{(1)} \\ e^{(2)} \\ \vdots \\ e^{(m)} \end{matrix} \right] = \cfrac{1}{m} X^{T} e = \cfrac{1}{m} X^{T} (X \theta - y) \end{aligned} ∂θ0∂J(θ0,θ1)∂θ1∂J(θ0,θ1) = m1i=1∑me(i)m1i=1∑me(i)x(i) = m1(e(1)+e(2)+⋯+e(m))m1(e(1)+e(2)+⋯+e(m))x(i) =m1[1x(1)1x(2)⋯⋯1x(m)] e(1)e(2)⋮e(m) =m1XTe=m1XT(Xθ−y)
- 由上述推导得
Δ θ = 1 m X T e \Delta{\theta} = \cfrac{1}{m} X^{T} e Δθ=m1XTe
θ : = θ − α Δ θ = θ − α 1 m X T e \theta := \theta - \alpha \Delta{\theta} = \theta - \alpha \cfrac{1}{m} X^{T} e θ:=θ−αΔθ=θ−αm1XTe
Python实现
导包
import numpy as np
import matplotlib.pyplot as plt
数据预处理
x = np.array([4, 3, 3, 4, 2, 2, 0, 1, 2, 5, 1, 2, 5, 1, 3])
y = np.array([8, 6, 6, 7, 4, 4, 2, 4, 5, 9, 3, 4, 8, 3, 6])m = len(x)x = np.c_[np.ones([m, 1]), x]
y = y.reshape(m, 1)
theta = np.zeros([2, 1])
迭代过程
alpha = 0.01
iter_cnt = 1000 # 迭代次数
cost = np.zeros([iter_cnt]) # 代价数据for i in range(iter_cnt):h = x.dot(theta) # 估计值error = h - y # 误差值cost[i] = 1 / (2 * m) * error.T.dot(error) # 代价值# 更新参数delta_theta = 1 / m * x.T.dot(error)theta -= alpha * delta_theta
数据可视化
# 回归结果
plt.scatter(x[:, 1], y, c='blue')
plt.plot(x[:, 1], h, 'r-')
plt.show()# 代价结果
plt.plot(cost)
plt.show()
完整代码
import numpy as np
import matplotlib.pyplot as pltx = np.array([4, 3, 3, 4, 2, 2, 0, 1, 2, 5, 1, 2, 5, 1, 3])
y = np.array([8, 6, 6, 7, 4, 4, 2, 4, 5, 9, 3, 4, 8, 3, 6])m = len(x)x = np.c_[np.ones([m, 1]), x]
y = y.reshape(m, 1)
theta = np.zeros([2, 1])alpha = 0.01
iter_cnt = 1000 # 迭代次数
cost = np.zeros([iter_cnt]) # 代价数据for i in range(iter_cnt):h = x.dot(theta) # 估计值error = h - y # 误差值cost[i] = 1 / (2 * m) * error.T.dot(error) # 代价值# 更新参数delta_theta = 1 / m * x.T.dot(error)theta -= alpha * delta_theta# 线性拟合结果
plt.scatter(x[:, 1], y, c='blue')
plt.plot(x[:, 1], h, 'r-')
plt.show()# 代价结果
plt.plot(cost)
plt.show()
线性拟合结果

代价结果

相关文章:

【机器学习】【线性回归】梯度下降
文章目录 [toc]数据集实际值估计值估计误差代价函数学习率参数更新Python实现导包数据预处理迭代过程数据可视化完整代码 线性拟合结果代价结果 个人主页:丷从心 系列专栏:机器学习 数据集 ( x ( i ) , y ( i ) ) , i 1 , 2 , ⋯ , m \left(x^{(i)} , …...
JMeter逻辑控制器之While控制器
JMeter逻辑控制器之While控制器 1. 背景2.目的3. 介绍4.While示例4.1 添加While控制器4.2 While控制器面板4.3 While控制器添加请求4.3 While控制器应用场景 1. 背景 存在一些使用场景,比如:某个请求必须等待上一个请求正确响应后才能开始执行。或者&…...

记录 Docker 外部访问的基本操作
目录 1. 启动 docker 时挂载本地目录2. 外部访问 docker 容器 (-p/-P)3. 无法连接 docker 内 SSH 解决方案 1. 启动 docker 时挂载本地目录 # 将本地 D:/SDK 目录 挂载到 容器里的 /mnt/host 目录中 # 注意:-v /d/SDK:/mnt/host/ 必须放到 IMAGE_ID 前面才行 # …...
:BannerMessagePreference)
【Android 13】使用Android Studio调试系统应用之Settings移植(六):BannerMessagePreference
文章目录 一、篇头二、系列文章2.1 Android 13 系列文章2.2 Android 9 系列文章2.3 Android 11 系列文章三、BannerMessagePreference的移植3.1 新的问题:找不到 R.dimen.settingslib_preferred_minimum_touch_target3.2 问题分析(一)3.2.1 资源定义的位置3.2.2 检查依赖3.2…...

Python 变量
打印输出内容 print(‘rumenle’) print(‘haode’) 缩进需要tab 注释将需要注释的部分开头用# 多行注释 1、用你也可以左键选中我们需要注释的代码,松开,按:Ctrl/,就完成相同效果注释 2、把要注释的内容放到三个引号对里面 …...

ComfyUI如何中文汉化
comfyui中文地址如下: https://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translationhttps://github.com/AIGODLIKE/AIGODLIKE-ComfyUI-Translation如何安装? 1. git安装 进入项目目录下的custom_nodes目录下,然后进入控制台,运…...
Glary Utilities Pro - 电脑系统优化全面指南:详尽使用教程
软件简介: Glary Utilities Pro 是一款全面的电脑优化工具,它旨在帮助用户提升计算机的性能和稳定性。这款软件提供了多种功能,包括系统清理、优化、修复以及保护。通过一键扫描,它可以识别并清除无用文件、临时数据、注册表错误等…...

1.4分页和排序
排序: -- 分页(limit)和排序(order by) -- 排序:升序ASC,降序DESC -- ORDER BY 通过字段排序,怎么排 -- 查询的结果根据成绩降序,升序 SELECT s.studentno,studentname,sub.subjectname,studentresult FROM student s RIGHT JO…...

Modbus转Profinet,不会编程也能用!轻松快上手!
Modbus转Profinet是一种用于工业自动化领域的通信协议转换器,可以将Modbus协议转换为Profinet协议,实现设备之间的数据交换与通信。这个工具的使用非常简单,即使没有编程经验的人也可以轻松上手。即使不会编程的人也可以轻松快速上手使用Modb…...
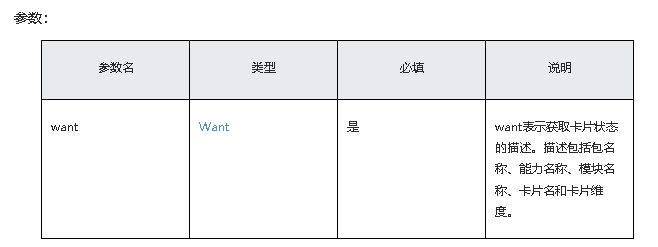
鸿蒙原生应用/元服务开发-Stage模型能力接口(十)下
ohos.app.form.FormExtensionAbility (FormExtensionAbility) 系统能力:SystemCapability.Ability.Form 示例 import FormExtensionAbility from ohos.app.form.FormExtensionAbility; import formBindingData from ohos.app.form.formBindingData; import formP…...

QT QPluginloader 加载失败,出现Unknown error 0x000000c1的问题
最近在学习Qt的插件开发,在加载插件时,一直失败,用如下代码加载并打印错误信息。 QDir dir("./testplugin.dll"); QPluginLoader pluginLoader(dir.absolutePath());//需要绝对路径 pluginLoader.load(); qDebug()<< "…...

众和策略:今年首次!A股罕见一幕
岁末,A股走出了不常见的行情。 这儿指的不单单是指数上涨。今天上午,A股逾3900只个股上涨,昨日逾4400只个股上涨,前天逾3700只个股上涨。据通达信数据显现,这种连续的普涨行情在本年还是头一次。 本年10月底…...
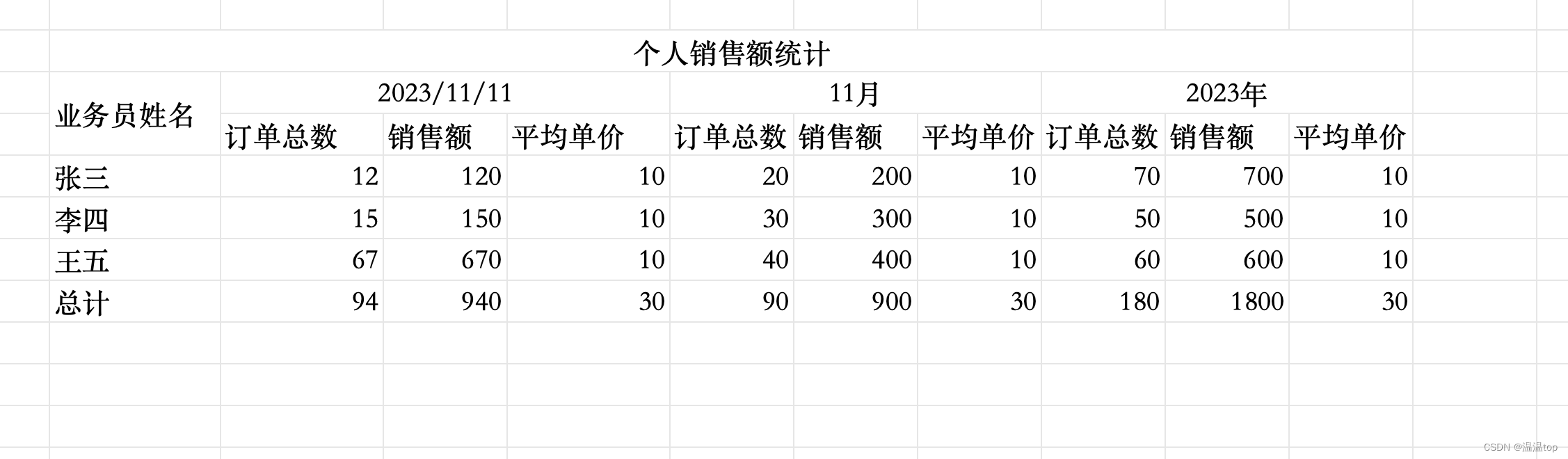
EasyExcel实现动态表头(注解实现)
要实现上述动态头,按每日统计,每月统计,每年统计。而时间是一直变化,所以我们需要表头也一直动态生成。 首先,我们需要定义所需要实体类 public class CountDayData {ExcelProperty(value "业务员姓名")p…...

什么是工厂方法模式,工厂方法模式解决了什么问题?
工厂方法模式是一种创建型设计模式,它定义了一个用于创建对象的接口,但将实际的实例化过程延迟到子类中。这样,客户端代码在不同的子类中实例化具体对象,而不是直接实例化具体类。工厂方法模式允许一个类的实例化延迟到其子类&…...
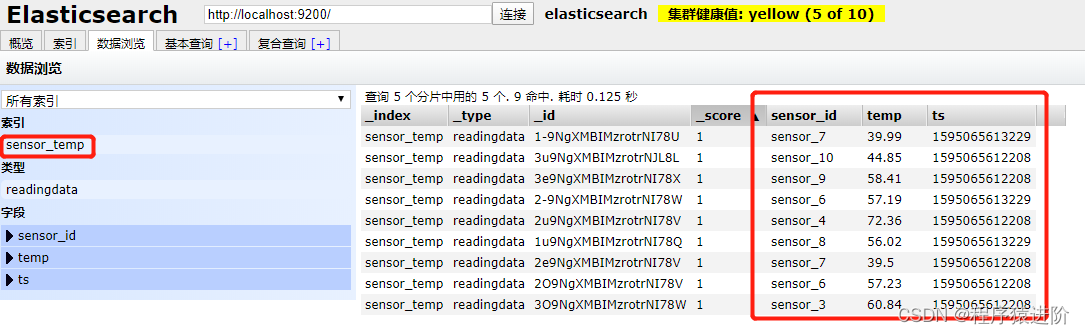
Flink 输出至 Elasticsearch
【1】引入pom.xml依赖 <dependency><groupId>org.apache.flink</groupId><artifactId>flink-connector-elasticsearch6_2.12</artifactId><version>1.10.0</version> </dependency>【2】ES6 Scala代码,自动导入的…...
web三层架构
目录 1.什么是三层架构 2.运用三层架构的目的 2.1规范代码 2.2解耦 2.3代码的复用和劳动成本的减少 3.各个层次的任务 3.1web层(表现层) 3.2service 层(业务逻辑层) 3.3dao 持久层(数据访问层) 4.结合mybatis简单实例演示 1.什么是三层架构 三层架构就是把…...

智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于厨师算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.厨师算法4.实验参数设定5.算法结果6.参考文献7.MA…...
写在2023年末,软件测试面试题总结
大家好,最近有不少小伙伴在后台留言,得准备年后面试了,又不知道从何下手!为了帮大家节约时间,特意准备了一份面试相关的资料,内容非常的全面,真的可以好好补一补,希望大家在都能拿到…...
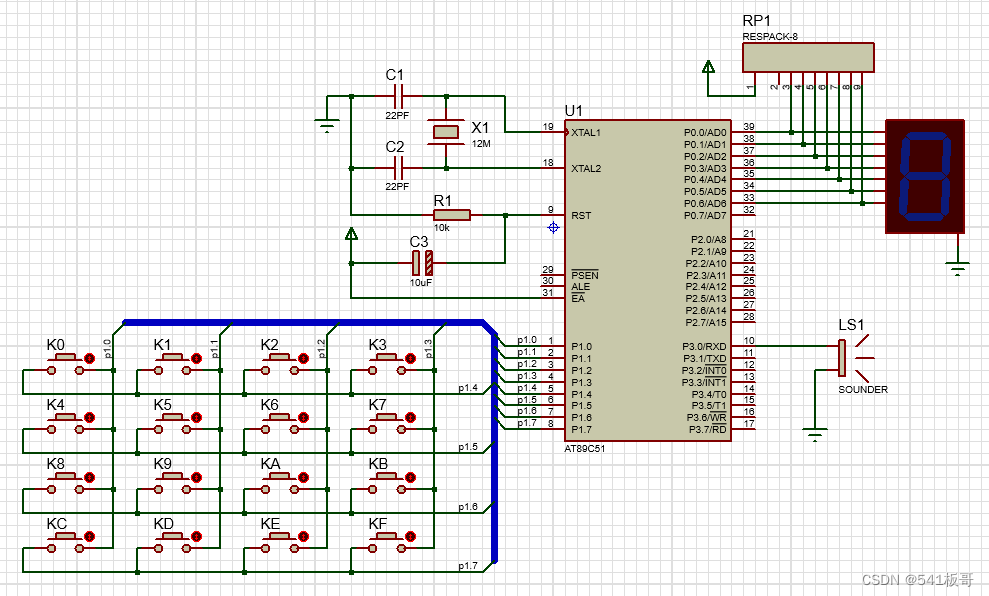
51系列--数码管显示的4X4矩阵键盘设计
本文介绍基于51单片机的4X4矩阵键盘数码管显示设计(完整Proteus仿真源文件及C代码见文末链接) 一、系统及功能介绍 本设计主控芯片选用51单片机,主要实现矩阵键盘对应按键键值在数码管上显示出来,矩阵键盘是4X4共计16位按键&…...
医院绩效考核系统源码,java源码,商业级医院绩效核算系统源码
医院绩效定义: “医院工作量绩效方案”是一套以工作量(RBRVS,相对价值比率)为核算基础,以工作岗位、技术含量、风险程度、服务数量等业绩为主要依据,以工作效率和效益、工作质量、患者满意度等指标为综合考…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
