Leetcode.2359 找到离给定两个节点最近的节点
题目链接
Leetcode.2359 找到离给定两个节点最近的节点 Rating : 1715
题目描述
给你一个 n个节点的 有向图 ,节点编号为 0到 n - 1,每个节点 至多 有一条出边。
有向图用大小为 n下标从 0开始的数组 edges表示,表示节点 i有一条有向边指向 edges[i]。如果节点 i没有出边,那么 edges[i] == -1。
同时给你两个节点 node1和 node2。
请你返回一个从 node1和 node2都能到达节点的编号,使节点 node1和节点 node2到这个节点的距离 较大值最小化。如果有多个答案,请返回 最小 的节点编号。如果答案不存在,返回 -1。
注意 edges可能包含环。
示例1:
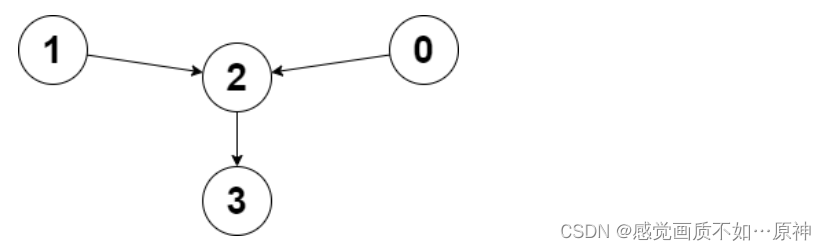
输入:edges = [2,2,3,-1], node1 = 0, node2 = 1
输出:2
解释:从节点 0 到节点 2 的距离为 1 ,从节点 1 到节点 2 的距离为 1 。
两个距离的较大值为 1 。我们无法得到一个比 1 更小的较大值,所以我们返回节点 2 。
示例2:

输入:edges = [1,2,-1], node1 = 0, node2 = 2
输出:2
解释:节点 0 到节点 2 的距离为 2 ,节点 2 到它自己的距离为 0 。
两个距离的较大值为 2 。我们无法得到一个比 2 更小的较大值,所以我们返回节点 2 。
提示:
- n==edges.lengthn == edges.lengthn==edges.length
- 2<=n<=1052 <= n <= 10^52<=n<=105
- −1<=edges[i]<n-1 <= edges[i] < n−1<=edges[i]<n
- edges[i]!=iedges[i] != iedges[i]!=i
- 0<=node1,node2<n0 <= node1, node2 < n0<=node1,node2<n
解法一:BFS
一个比较容易想到的解法是,对于 node1和 node2分别通过 BFS 计算其 到各个点的距离矩阵 d1和 d2。
对于 d1和 d2,我们从小到大遍历,更新最小的 较大值。
时间复杂度:O(n)O(n)O(n)
代码:
class Solution {
public:
// 建图unordered_map<int,vector<int>> g;//bfs 求起点 root 到各个点的距离矩阵void bfs(int root,vector<int> & dist){queue<int> q;q.push(root);int step = 0;while(!q.empty()){int sz = q.size();for(int i = 0;i < sz;i++){auto t = q.front();q.pop();dist[t] = step;for(auto v:g[t]){if(dist[v] != -1) continue;q.push(v);}}step++;}}int closestMeetingNode(vector<int>& edges, int node1, int node2) {int n = edges.size();for(int i = 0;i < n;i++){if(edges[i] == -1) continue;int a = i, b = edges[i];g[a].push_back(b);}vector<int> a(n,-1),b(n,-1);bfs(node1,a);bfs(node2,b);/*for(int i = 0;i < n;i++){printf("i = %d , d1 = %d , d2 = %d\n",i,a[i],b[i]);}*/int dist = 1e9;int idx = -1;for(int i = 0;i < n;i++){if(a[i] == -1 || b[i] == -1) continue;int d = max(a[i],b[i]);if(dist > d){dist = d;idx = i;}}return idx;}
};
解法二:遍历
题目给定地有向图实际上是一个 基环树,因为每一个结点的 出边最多只有一条,所以实际上我们不需要建图,只需要直接循环遍历即可。
时间复杂度:O(n)O(n)O(n)
代码:
class Solution {
public:int closestMeetingNode(vector<int>& edges, int node1, int node2) {int n = edges.size();auto dfs = [&](int u) -> vector<int>{vector<int> dist(n,1e9);int d = 0;while(u != -1 && dist[u] == 1e9){dist[u] = d;d++;u = edges[u];}return dist;};auto d1 = dfs(node1);auto d2 = dfs(node2);int ans = 1e9,idx = -1;for(int i = 0;i < n;i++){if(d1[i] == 1e9 || d2[i] == 1e9) continue;int d = max(d1[i],d2[i]);if(ans > d){ans = d;idx = i;}}return idx;}
};
相关文章:

Leetcode.2359 找到离给定两个节点最近的节点
题目链接 Leetcode.2359 找到离给定两个节点最近的节点 Rating : 1715 题目描述 给你一个 n个节点的 有向图 ,节点编号为 0到 n - 1,每个节点 至多 有一条出边。 有向图用大小为 n下标从 0开始的数组 edges表示,表示节点 i有一条…...
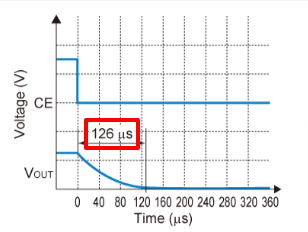
DCDC/LDO Auto-Discharge
1、概念 When using a capacitor with large capacity value in VOUT side, the VOUT pin voltage might not immediately fall to the ground level when the EN(CE,CONTROL) pin is switched from the active mode to the standby mode. By adding N-channel transistor to …...

linux 中的log
linux 中的log 由于内核的特殊性,我们不能使用常规的方法查看内核的信息。下面介绍几种方法。 1 printk()打印内核消息。 2 管理内核内存的daemon(守护进程) Linux系统当中最流行的日志记录器是Sysklogd,Sysklogd 日志记录器由…...
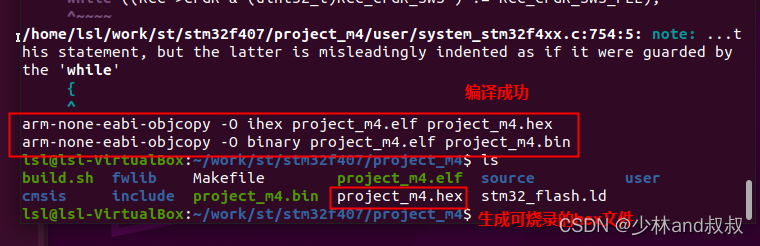
基于ubuntu的STM32嵌入式软件开发(四)——应用软件工程的修改、Makefile及编译脚本的编写
本文主要介绍基于标准库函数移植的STM32的应用软件工程的修改,主要涉及到文件内容修改、Makefile文件编写、编译脚本编写等内容,其中编译脚本是基于arm-none-eabi-gcc的交叉编译器撰写的。程序亲测可以正常编译,生成.bin和.hex的可烧录镜像文…...

MQTT协议分析
目录 一、前言 二、MQTT协议概述 概念 基本原理 MQTT协议的结构 MQTT的QoS机制 QoS 0:最多一次传输 QoS 1:至少一次传输 QoS 2:恰好一次传输 三、MQTT的应用场景 四、MQTT的优点和缺点 五、MQTT协议的实现 六、实战体验MQTT …...
基于树莓派4B设计的音视频播放器(从0开始)
一、前言 【1】功能总结 选择树莓派设计一款家庭影院系统,可以播放本地视频、网络视频直播、游戏直播、娱乐直播、本地音乐、网络音乐,当做FM网络收音机。 软件采用Qt设计、播放器引擎采用ffmpeg。 当前的硬件选择的是树莓派4B,烧写官方系统,完成最终的开发。 本篇文章主…...
MSF手机渗透实验(未成功)(CVE-2019-2215 Binder UA)
1. 前言 最近想利用metasploit对手机进行依次渗透实验。 通过查看最近三年的安卓漏洞,我对CVE-2019-2215这个漏洞很感兴趣。 幸运的是,metasploit里就有这个漏洞的攻击payload,于是我就开始试试了。 msf6 > search binderMatching Mod…...
系列十二、MySQL管理
一、系统数据库 Mysql数据库安装完成后,自带了一下四个数据库,具体作用如下:二、常用工具 2.1、mysql 2.1.1、概述 该mysql不是指mysql服务,而是指mysql的客户端工具。 2.1.2、语法 # 语法 : mysql [options] [dat…...

[游戏架构] 有限状态机的实际应用
什么是有限状态机 有限状态机(Finite State Machine,简称FSM)是一种常用的计算机科学中的建模工具,用于描述由离散状态和状态之间的转换组成的系统。它主要由一个有限的状态集合、一个初始状态、一个输入事件集合、状态之间的转换…...

【站外SEO】如何利用外部链接来提高你的网站排名
随着互联网的快速发展,越来越多的企业开始注重SEO优化,以提升自己的网站排名,增加流量和曝光度。 而站外SEO作为SEO的重要组成部分,对于提升网站排名具有不可忽视的作用。 站外SEO主要是通过外部链接来提高网站的排名。而GPB外链…...
)
OSCP-课外4(修复web访问、Mysql UDF提权)
目录 难度 一、主机发现与端口扫描 二、Web信息收集 站点目录扫描 搜索phpmailer的漏...
深信服面经---云计算方向(附问题知识点解析)
深信服面经---云计算高级开发一、一面问题概览二、实操相关三、复盘对问题答案进行整理(查漏补缺)3.1、go语言简单了解3.2、项目中成就感最大或挑战最大的地方3.3、项目问题---协议头引入之后,包的大小增加了多少3.4、如何建立缓存3.5、cache…...
MySQL面试题-基础篇
目录 前言 数据库基础 1.什么是关系型数据库和非关系型数据库? 2.什么是 SQL? 3.MySQL 有什么优点? 4.MySQL 的基础架构? 存储引擎 1.MySQL 支持哪些存储引擎?默认使用哪个? 2.MySQL 存储引擎架构了解吗&…...
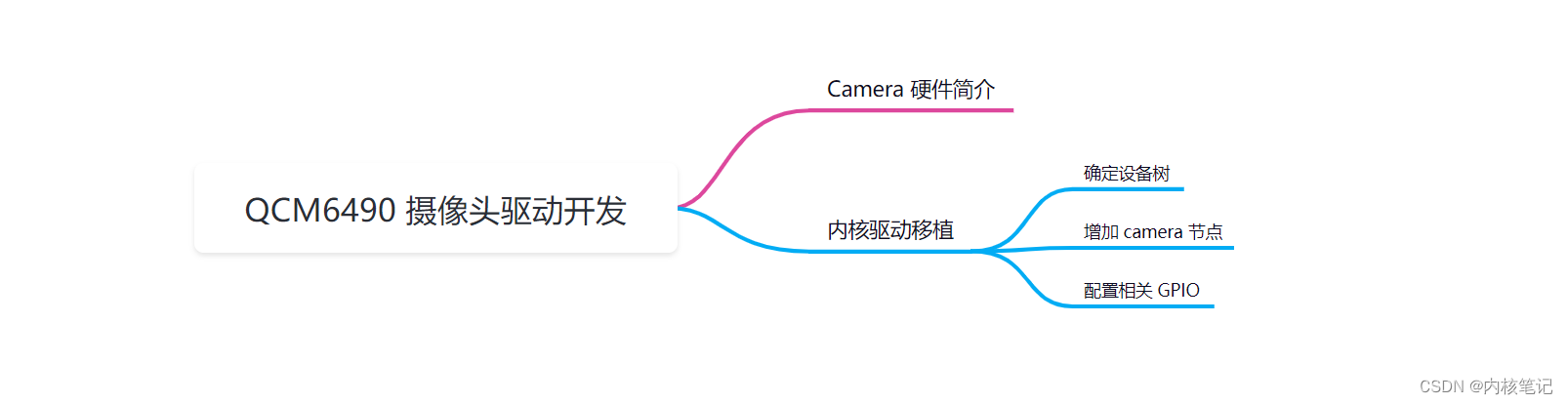
高通平台开发系列讲解(摄像头篇)QCM6490 上摄像头驱动开发
文章目录 一、Camera 硬件简介二、内核驱动移植2.1、确定设备树2.2、增加 camera 节点2.3、配置相关 GPIO沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇将介绍 qcm6490 摄像头驱动开发。 一、Camera 硬件简介 摄像头连接器一般会包含 Mipi 信号、mclk、供电、re…...

MOV压敏电阻应用推荐及选型要点说明
ESD器件-MOV压敏电阻是一种非线性的电阻元器件产品,具有瞬态电压抑制功能,能够吸收电路中多余的电流,可保护一些敏感电路及其他电子产品设备的电路不受ESD、雷击瞬态浪涌电流的危害。对于它的一些应用范围,优恩小编在这里举例说明…...

Pytorch学习笔记(8):正则化(L1、L2、Dropout)与归一化(BN、LN、IN、GN)
目录 一、正则化之weight_decay(L2正则) 1.1 正则化及相关概念 1.2 正则化策略(L1、L2) (1)L1正则化 (2)L2正则化 1.3 L2正则项——weight_decay 二、正则化之Dropout 2.1 Dr…...

Azure OpenAI 官方指南 01|GPT-3 的原理揭秘与微调技巧
Azure OpenAI 服务在微软全球 Azure 平台正式发布后,迅速成为众多用户最关心的服务之一。 Azure OpenAI 服务允许用户通过 REST API 访问 OpenAI 的强大语言模型,包括 GPT-3、Codex 和 Embeddings 模型系列。本期,我们将为您揭秘 Azure Open…...

神垕古镇景区三方背后的博弈,争夺许昌第一家5A景区主导权
钧 瓷 内 参 第37期(总第368期) 2023年3月2日 神垕古镇景区景域,建业,孔家三方背后的博弈,争夺许昌第一家5A景区主导权 在博弈论(Game Theory)经济学中,“智猪博弈”是一个著名的…...

【C++】vector的模拟实现(SGI版本)
吃不了自律的苦,又接受不了平庸的罪。想让自己变好,但又想舒服些。 你啊你……要么就不要去想,想了又不去做,犹犹豫豫,徘徊不前,患得患失… 文章目录一、四种构造函数1.vector的框架和无参构造2.构造函数调…...

【9】SCI易中期刊推荐——工程技术-计算机:软件工程(中科院4区)
🚀🚀🚀NEW!!!SCI易中期刊推荐栏目来啦 ~ 📚🍀 SCI即《科学引文索引》(Science Citation Index, SCI),是1961年由美国科学信息研究所(Institute for Scientific Information, ISI)创办的文献检索工具,创始人是美国著名情报专家尤金加菲尔德(Eugene Garfield…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
