MyBatisPlus之逻辑删除
系列文章目录
提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加
MyBatisPlus之逻辑删除
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 系列文章目录
- 前言
- 一、什么是逻辑删除
- 二、逻辑删除的使用
- 三、自动填充
- 自动填充步骤
- 总结
前言
提示:这里可以添加本文要记录的大概内容:
在学习MyBatisPlus的过程中,逻辑删除是一个比较重要的知识点。逻辑删除是指使用一个特殊的字段来表示数据库表中的一条记录是否被删除了(或是否存在),例如为数据库表中的每一条记录都增加一个is_delete字段,当is_delete为1时,表示该记录已经被删除了,当is_delete为0时,表示该记录还有效。与逻辑删除相对的就是物理删除,指直接从数据库中删除记录。
逻辑删除是为了方便数据恢复和保护数据本身价值等的一种方案,但实际就是删除。如果需要频繁查出来看就不应使用逻辑删除,而是以一个状态去表示。
希望通过本文的介绍,大家对MyBatisPlus的逻辑删除有一个初步的了解。后续会详细介绍逻辑删除的实现在此基础上。
提示:以下是本篇文章正文内容,下面案例可供参考
一、什么是逻辑删除
逻辑删除是一种用于表示数据删除状态的数据处理方式。在逻辑删除中,数据并没有从数据库中真正被删除,而是通过标记或更新一个字段来表示该数据已被删除。
常见的实现方式是在数据库表中添加一个名为is_deleted的字段,并将其设置为1或true来表示数据已被删除,设置为0或false来表示数据未被删除。这样,在查询数据时,可以通过添加条件来过滤出已被删除的数据。此时增删改查的Sql语句发生变化:
- 插入: 不作限制
- 查找: 追加where条件过滤掉已删除数据。例如 select id,name,deleted from user where deleted=0
- 更新: 追加where条件防止更新到已删除数据。
- 删除: 转变为更新,例如 update user set deleted=1 where id = 1 and deleted=0
逻辑删除的好处是可以保留数据的历史记录,以便在需要时进行恢复或审计。同时,它还可以避免由于误操作或数据完整性问题导致的数据丢失。
需要注意的是,逻辑删除只是一种数据处理方式,并不代表数据真正被删除。在实际应用中,需要根据具体情况选择合适的数据处理方式,并确保数据的安全性和完整性。
二、逻辑删除的使用
1.在配置文件配置逻辑删除
# mybatis-plus相关配置
mybatis-plus:# 全局配置global-config:db-config:# 全局逻辑删除的字段名logic-delete-field: deleted# 逻辑已删除值(默认为 1)logic-delete-value: 1# 逻辑未删除值(默认为 0)logic-not-delete-value: 02.修改实体类,添加逻辑删除属性
@Data
@NoArgsConstructor
@AllArgsConstructor
public class Student extends Model<Student> {@TableId(value = "sid")private Integer id;@TableField("sname")private String name;private String email;private String gender;private Integer age;@Versionprivate Integer version;@TableLogicprivate Integer deleted;
}3.修改数据库表,添加一列整型deleted字段并设置默认值为0
4.测试删除和查询方法,会看到删除时将deleted字段变为1,查询时添加条件deleted=0
三、自动填充
因为存在逻辑删除字段,所以在向数据库插入数据时,都需要将deleted字段的值设置为 0。每次插入数据都要设置这个值,非常繁琐。因此,MyBatis-Plus 提供了自动填充功能来解决这个问题。
自动填充步骤
1.为实体类的自动填充字段添加@TableField
@TableLogic
// 自动填充字段
@TableField(fill = FieldFill.INSERT)
private Integer deleted;填充策略:
- DEFAULT:默认不处理
- INSERT:插入操作填充字段
- UPDATE:更新操作填充字段
- INSERT_UPDATE:插入操作和更新操作均填充字段
2.自定义填充类实现MetaObjectHandler接口
@Component
public class MyMetaObjectHandler implements MetaObjectHandler {/*** 插入时填充逻辑* @param metaObject 元对象*/@Overridepublic void insertFill(MetaObject metaObject) {/*** 参数1:填充字段名* 参数2:参数值* 参数3:元对象*/this.setFieldValByName("deleted", 0, metaObject);}/*** 更新时填充逻辑* @param metaObject*/@Overridepublic void updateFill(MetaObject metaObject) {}
}总结
提示:这里对文章进行总结:
- 什么是逻辑删除:逻辑删除是指文件或数据没有被真正删除,只是通过对数据进行标注,使其无法被识别到。这种删除操作通常是可逆的,即可以使用适当的工具或软件将删除的文件或数据恢复出来。
- 常规逻辑删除:在数据库表中添加一个is_delete字段,值为0表示数据未删除,值为1表示数据已删除。插入数据时,该字段默认为0。删除数据时,将该值设置为1。查询和更新数据时都将is_delete=0作为条件,只查询和更新未删除的数据。
相关文章:

MyBatisPlus之逻辑删除
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 MyBatisPlus之逻辑删除 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 系列文章目录前言一、什么是逻辑删…...
在macOS中搭建.NET MAUI开发环境
文章目录 准备安装扩展安装 .NET安装工作负载安装 Xcode 命令行工具调试安卓应用安装 JDK安装 Android SDK 安装 Android 模拟器安装模拟器安装镜像创建虚拟机 同意许可条款创建 MAUI 项目调试 MAUI 应用切换调试目标 参考资料 准备 一台 macOS Monterey 以上的电脑安装 XCode…...
[NCTF 2022]calc
[NCTF 2022]calc 考点:python环境变量注入 打开题目,F12有hint 访问一下得到源码 app.route("/calc",methods[GET]) def calc():ip request.remote_addrnum request.values.get("num")log "echo {0} {1} {2}> ./tmp/log…...
【pandas_不重复项计数】
听说WPS没有非重复项计数的功能,而office需要添加到数据模型之后,才可以使用该功能。而用pandas,既可以对重复项计数,又可以对非重复项计数。 # 使用提醒: # 1. xbot包提供软件自动化、数据表格、Excel、日志、AI等功能 # 2. pack…...
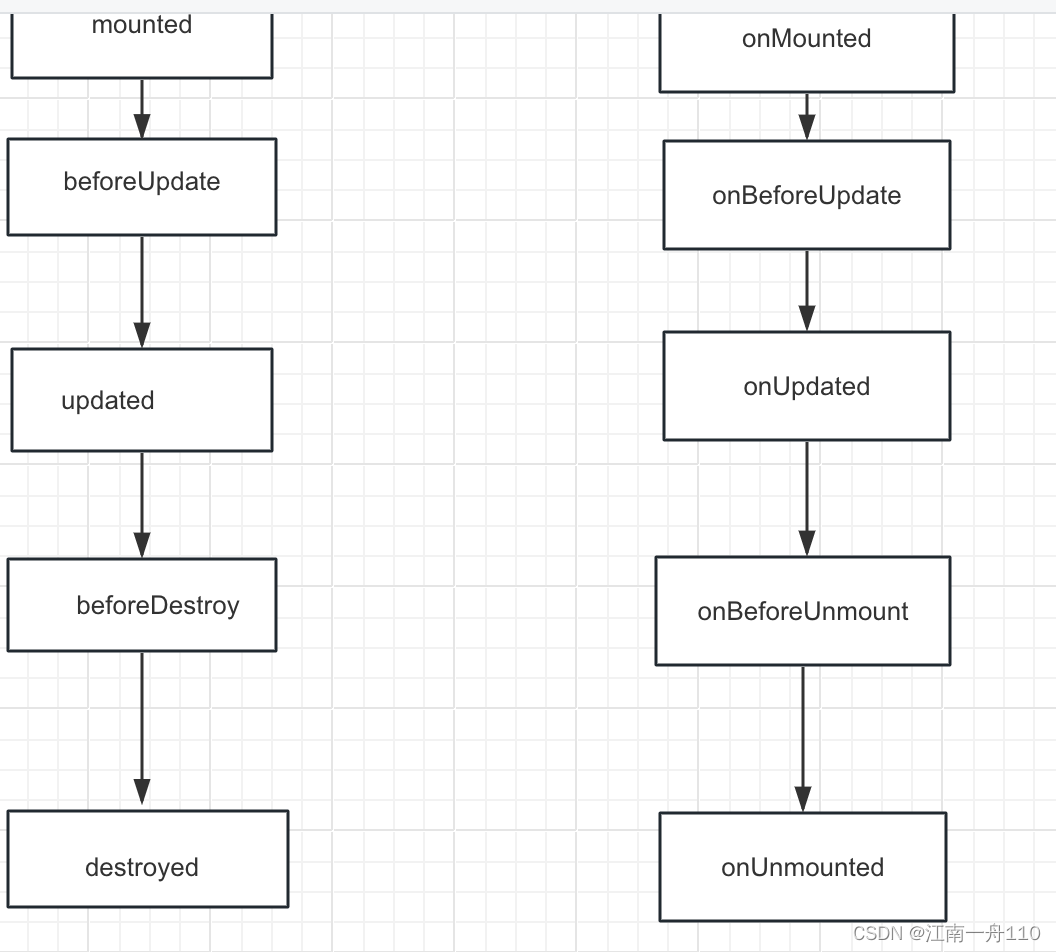
菜鸟学习vue3笔记-vue hooks初体验
import { ref } from "vue"; export default function () {let a1 ref(1);let a2 ref(5);let c ref(0);function add() {a1.value;a2.value;}return {add,a1,a2,c,}; }<template><div><p>第一个数字{{ a1 }}</p><p>第二个数字{{ a2…...

81 使用DFS和BFS解机器人的运动范围
问题描述:地上有一个m行n列的方格,从坐标[0,0]到坐标[m-1,n-1].一个机器人从坐标[0,0]的格子开始移动,他每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。 public int numB…...
vue-springboot基于JavaWeb的家装一体化商城平台guptn
针对用户需求开发与设计,该技术尤其在各行业领域发挥了巨大的作用,有效地促进了家装一体化的发展。然而,由于用户量和需求量的增加,信息过载等问题暴露出来,为改善传统线下管理中的不足,本文将提出一套基于…...

.NET进阶篇06-async异步、thread多线程2
知识须要不断积累、总结和沉淀,思考和写做是成长的催化剂web 内容目录 1、线程Thread 一、生命周期 二、后台线程 三、静态方法 1.线程本地存储 2.内存栅栏 四、返回值 2、线程池ThreadPool 一、工做队列 二、工做线程和IO线程 三、和Thread区别 四、定时器 1、线…...

java 方法
方法: 什么是方法,有什么用? 方法(英语单词:method)是可以完成某个特定功能的并且可以被重复利用的代码片段。 在 C 语言中,方法被称为“函数”。在 java 中不叫函数,叫做方法。 方法…...
HarmonyOS 组件通用属性之通用事件 文档参数讲解(点击事件)
我们组件中 会有很多通用的信息和方法 那么 首先 我们看通用事件 通用事件中 最常用的就是我们的点击事件 比如说 我们之前常写的 组件.onClick(()>{//事件逻辑 })但是 我们之前 都没有用它接参数 我们可以这样 Button("跳转").onClick((ewat: ClickEvent)>…...

毕业设计之开题报告
终于轮到我来写开题报告了,呃呃呃呃呃,目前有点难产了。想做的东西是关于区块链的后端设计实现,但是因为是完全原创之前没有类似的项目能去参考,所以其实有点慌的。 框架梳理 这是我们开题报告的要求: 包括题目研究的…...

【数据结构】详细剖析线性表
顺序表与链表的比较 导言一、线性表二、线性表的存储结构三、顺序表和链表的相同点四、顺序表与链表之间的差异五、存储结构的选择六、静态顺序表的基本操作七、无头结点单链表的基本操作结语 导言 大家好,很高兴又和大家见面啦!!࿰…...

通过数字证书对PDF电子文件进行数字签名/盖章
以下代码详细说明如何使用数字证书对PDF电子文件进行数字签名/盖章。PDF文件签署主要传递PDF文件,数字证书信息,签章图片3个信息。代码中需要的文件、数字证书、签章图片可访问开放签电子签章开源系统详细了解系统的实现与效果。也可通过gitee开源社区下…...

2007~2016 年税调经纬度及其所处的省市区县乡镇数据
之前给大家分享过一份税调企业经纬度及其所处的省市区县数据: 2007~2016 年税调企业地理信息数据(含经纬度及其所处的省市区县):https://rstata.duanshu.com/#/course/76d38022cd004b09b2aa09647936beb0 最近有培训班的小伙伴提出是否能根据税调企业经纬度来判断其所属的乡…...

SLAM学习入门--编程语言
文章目录 编程语言一、C/C++C 与 C++ 的区别(面向对象的特点)C++ 与 Python的区别判断struct的字节数static 作用Const 作用extern "C"的作用多态如何实现多态?虚函数虚函数怎么实现的?析构函数虚析构函数的作用virtual函数能不能用在构造函数中&#...

Go语言程序设计-第6章--方法
Go语言程序设计-第6章–方法 对象就是简单的一个值或者变量,并且拥有其方法,而方法是某种特定类型的函数。 6.1 方法的声明 方法的声明和普通函数的声明类似,只是在函数名字前面多了一个参数。这个参数把这个方法绑定到这个参数对应的类型…...
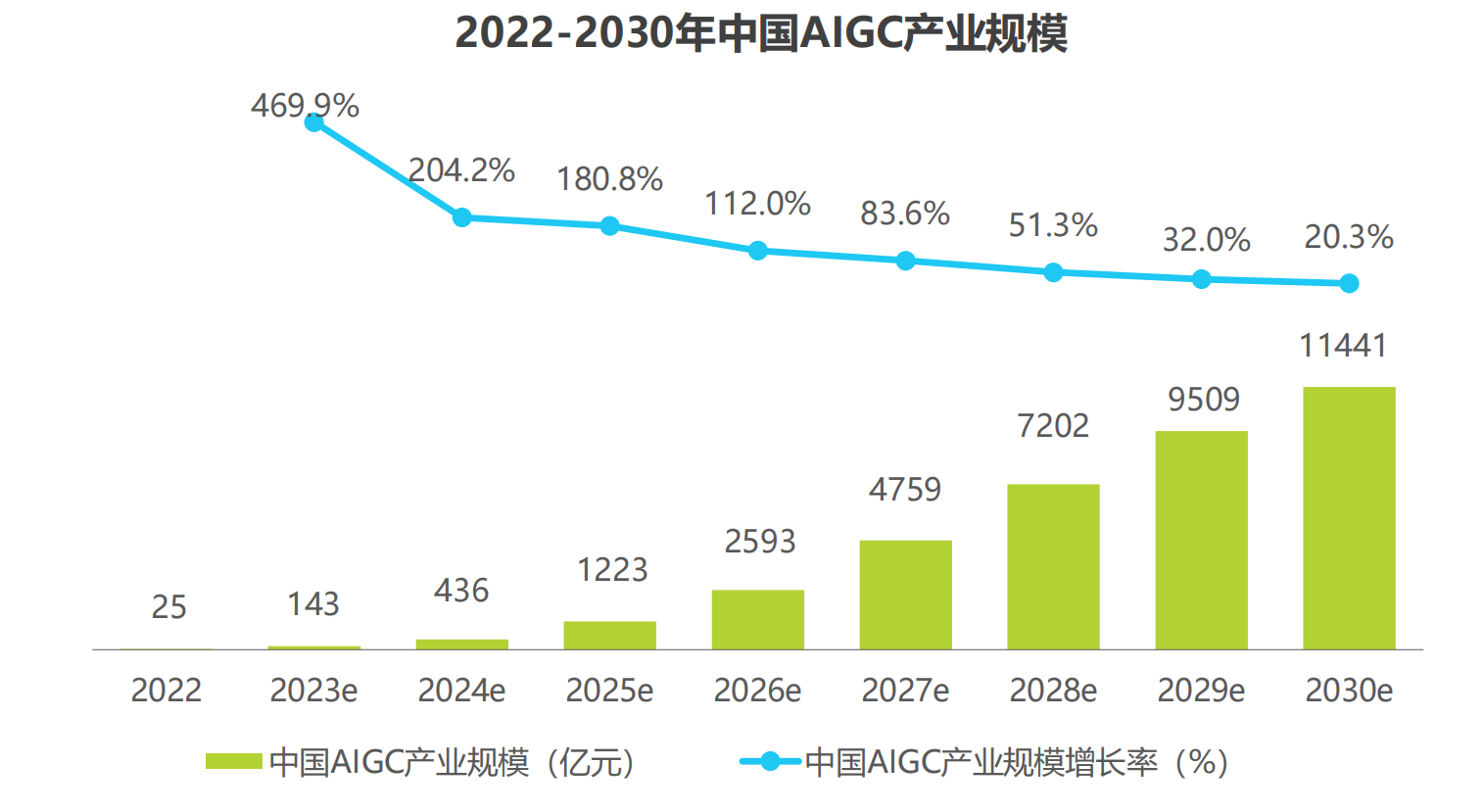
AI按理说应该最擅长理工,为啥先冲击文艺行业?
介绍 本人数据AI工程师,我的观点对全行业都有冲击,当AI大模型持续进化之时,没有一家公司能独善其身。 本文从产业架构上、论文体量、基础Pass能力、通用大模型、AI开源社区、业务属性大模型、内容消费工具、创作工具赛道、企业服务这些板块…...

蓝牙物联网移动硬件数据传输系统解决方案
随着传感器技术、网络技术和数据传输技术的不断发展,人们对智能设备的需求日渐增强,利用传感器技术可以对周围环境进行准确和全面的感知,获取到实时信息,从而在网络中进行传输和共享,再通过服务器对各种数据进行保存、分析和挖掘等…...

Linux下Web服务器工作模型及Nginx工作原理详解
文章目录 1. 工作模型概述1.1 阻塞、非阻塞、同步、异步浅析1.2 Web服务器处理并发请求的方式 2. Linux下的I/O模型2.1 常用I/O模型2.2 对比以上模型 3. Nginx工作原理3.1 Nginx基本架构3.2 Nginx代码结构3.3 Nginx工作流程3.4 Nginx缓存机制3.5 Nginx缓存工具:Memc…...

AJAX: 整理2:学习原生的AJAX,这边借助express框架
1. npm install express 终端直接安装 2. 测试案例:Hello World! 新建一个express.js的文件,写入下方的内容 // 1. 引入express const express require(express)// 2. 创建服务器 const app express()// 3.创建路由规则 // request 是对请…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
