ubuntu多用户环境dockerbug,卸载重装docker流程
之前不小心误操作删除重装docker,结果删除没成功,更没法重装,每次apt install都会报一个docker错误,虽然不影响软件的常规安装~但是现在还是需要装一个完整docker,还是选择删除一下,重点是关闭服务,关闭服务就好卸载了。
Process: 32174 ExecStart=/usr/bin/dockerd --graph=/home/hxb/docker/lib/docker (code=exited, status=1/FAILURE)
(pid是动态的,提示是固定的)

为是hqw用户,但是老提示hxb用户,需要卸载docker重装,重装好多次还是同样的错误,卸载重点是“干净”,不干净就会重复报错。
彻底卸载docker
卸载docker
1.删除docker及安装时自动安装的所有包
apt-get autoremove docker docker-ce docker-engine docker.io containerd runc
2.查看docker是否卸载干净
dpkg -l | grep docker
dpkg -l |grep ^rc|awk '{print $2}' |sudo xargs dpkg -P # 删除无用的相关的配置文件
3.删除没有删除的相关插件
apt-get autoremove docker-ce-*
4.删除docker的相关配置&目录
rm -rf /etc/systemd/system/docker.service.d
rm -rf /var/lib/docker
5.确定docker卸载完毕
docker --version
下面是安装docker
- 更新apt软件包索引:
sudo apt update
- 安装必要的软件包,以允许apt通过HTTPS使用存储库:
sudo apt install apt-transport-https ca-certificates curl software-properties-common
- 添加Docker的官方GPG密钥:
curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo gpg --dearmor -o /usr/share/keyrings/docker-archive-keyring.gpg
- 添加Docker存储库:
echo "deb [arch=amd64 signed-by=/usr/share/keyrings/docker-archive-keyring.gpg] https://download.docker.com/linux/ubuntu $(lsb_release -cs) stable" | sudo tee /etc/apt/sources.list.d/docker.list > /dev/null
- 更新apt软件包索引:
sudo apt update
- 安装Docker引擎:
sudo apt install docker-ce docker-ce-cli containerd.io
- 启动Docker服务:
sudo systemctl start docker

- 验证Docker是否正确安装:
sudo docker run hello-world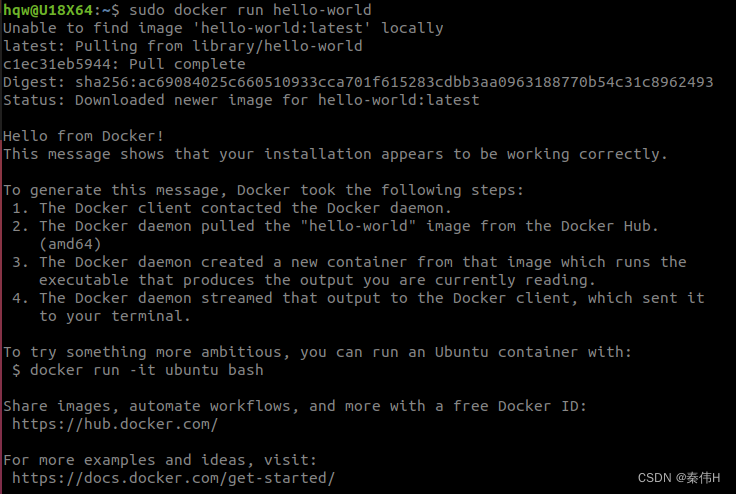
相关文章:

ubuntu多用户环境dockerbug,卸载重装docker流程
之前不小心误操作删除重装docker,结果删除没成功,更没法重装,每次apt install都会报一个docker错误,虽然不影响软件的常规安装~但是现在还是需要装一个完整docker,还是选择删除一下,重点是关闭服…...
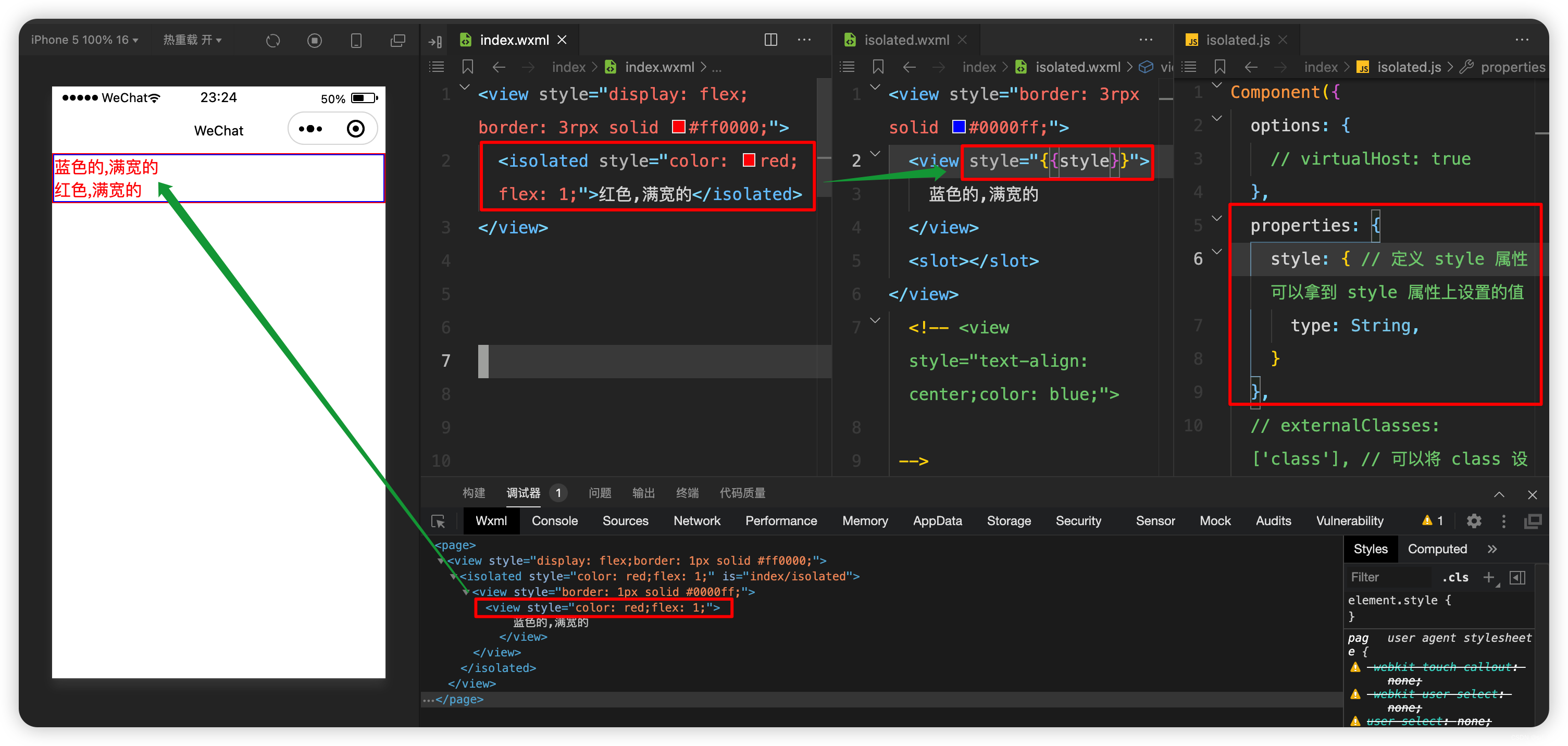
微信小程序开发系列-09自定义组件样式特性
微信小程序开发系列目录 《微信小程序开发系列-01创建一个最小的小程序项目》《微信小程序开发系列-02注册小程序》《微信小程序开发系列-03全局配置中的“window”和“tabBar”》《微信小程序开发系列-04获取用户图像和昵称》《微信小程序开发系列-05登录小程序》《微信小程序…...
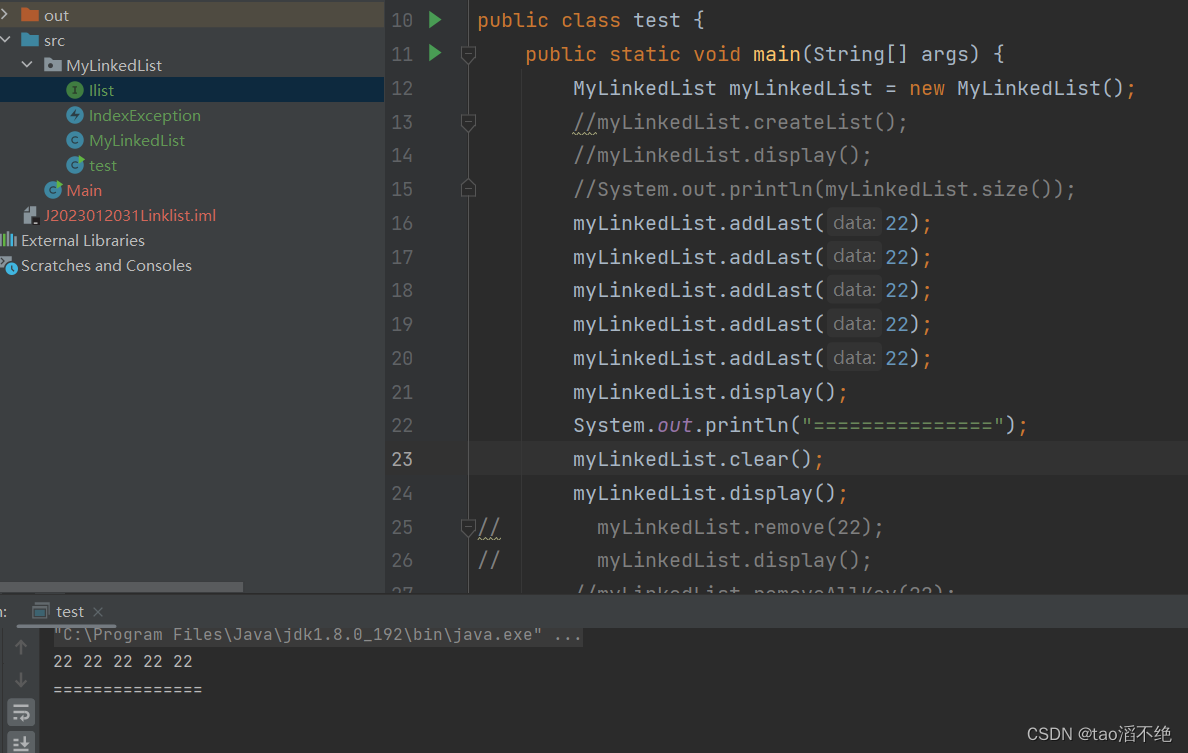
数据结构 模拟实现LinkedList单向不循环链表
目录 一、链表的简单介绍 二、链表的接口 三、链表的方法实现 (1)display方法 (2)size得到单链表的长度方法 (3)addFirst头插方法 (4)addLast尾插方法 (5…...

2023-12-24 LeetCode每日一题(收集足够苹果的最小花园周长)
2023-12-24每日一题 一、题目编号 1954. 收集足够苹果的最小花园周长二、题目链接 点击跳转到题目位置 三、题目描述 给你一个用无限二维网格表示的花园,每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| |j| 个苹果。 你将会买下正中心坐…...

Oracle 19c OCP 1z0 082考场真题解析第17题
考试科目:1Z0-082 考试题量:90 通过分数:60% 考试时间:150min 本文为云贝教育郭一军guoyJoe原创,请尊重知识产权,转发请注明出处,不接受任何抄袭、演绎和未经注明出处的转载。 17. Which three …...
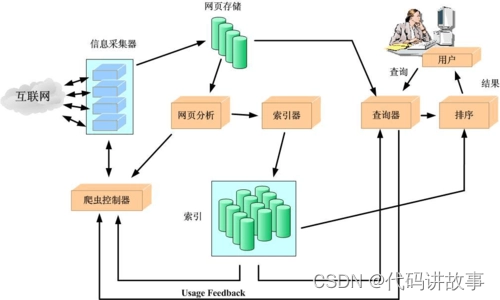
掌握这十几个Python库才是爬虫界的天花板,没有你搞不定的网站!实战案例:Python全网最强电影搜索工具,自动生成播放链接
掌握这十几个Python库才是爬虫界的天花板,没有你搞不定的网站!实战案例:Python全网最强电影搜索工具,自动生成播放链接。 用来爬虫的十几个Python库。只要正确选择适合自己的Python库才能真正提高爬虫效率,到达高效爬虫目的。 1.PyQuery from pyquery import PyQuery as …...
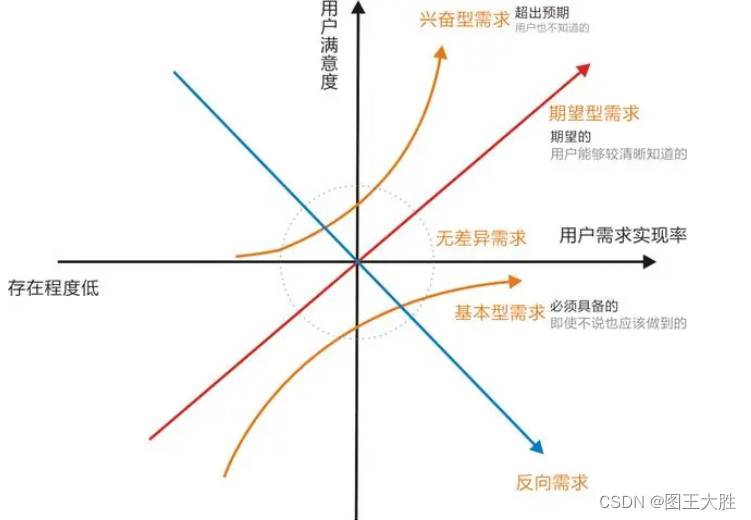
模型 KANO卡诺模型
本系列文章 主要是 分享 思维模型,涉及各个领域,重在提升认知。需求分析。 1 卡诺模型的应用 1.1 餐厅需求分析故事 假设你经营一家餐厅,你想了解客户对你的服务质量的满意度。你可以使用卡诺模型来收集客户的反馈,并分析客户的…...
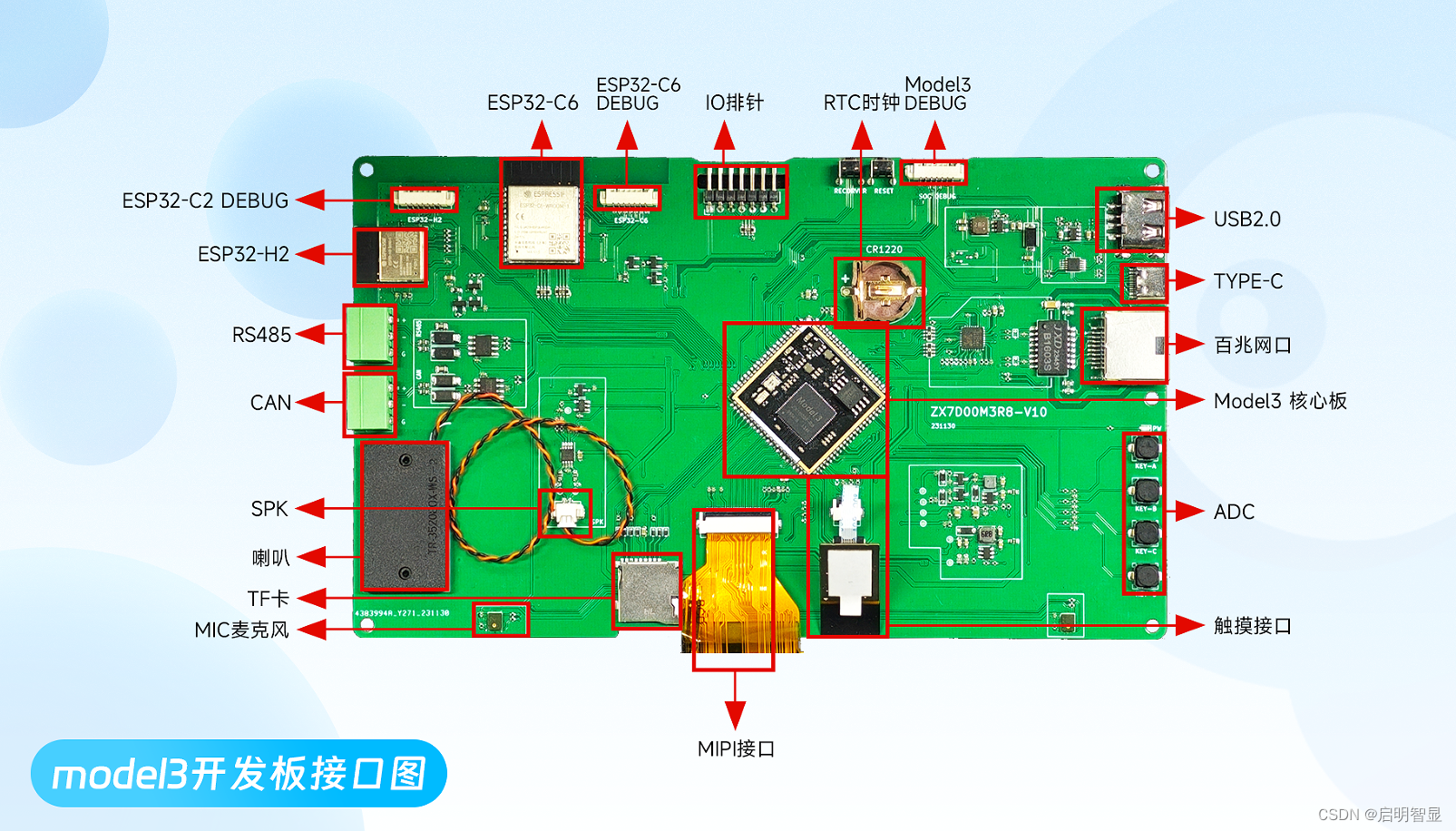
启明智显开源项目分享|基于Model 3c芯片的86中控面板ZX3D95CM20S-V11项目软硬件全开源
前言: 本文为4寸 480*480 RGB接口IPS全面触屏的86中控面板(RT-ThreadLVGL)软硬件开源干货内容,该项目是综合性非常强的RTOS系列项目!项目主控芯片使用 Model 3c,整体实现了简化版本的86中控面板的功能需求…...

Kind创建k8s - JAVA操作控制
kind 简介kind 架构安装 Kind (必备工具)docker官网kubectl官网kind官网校验安装结果 关于kind 命令 安装一个集群查看当前 Kubernetes 集群中的节点信息。查看当前命名空间下中的Pod(容器实例)的信息。使用 kind create cluster 安装,关于安…...
Qt sender()函数
sender函数原型: QObject *sender() const; 如果在由信号激活的插槽中调用该函数,返回指向发送信号的对象的指针,否则返回0,该指针仅在从该对象的线程上下文调用此函数的槽执行期间有效。 主要代码如下: 其中运用了Q…...
)
Java开发框架和中间件面试题(6)
目录 61.什么是Spring Batch? 62.请举例解释Required与Qualifier注解? 61.什么是Spring Batch? Spring batch是一个轻量级的,完善的批处理框架,他主要的目的在于帮助企业建立健壮,高效的批处理应用。Spri…...

附录E SQL入门之SQL保留字
本专栏目录 第1课 SQL入门之了解SQL 第2课 SQL入门之检索数据 第3课 SQL入门之排序检索数据 第4课 SQL入门之过滤数据 第5课 SQL入门之高级数据过滤 第6课 SQL入门之用通配符进行过滤 第7课 SQL入门之创建计算字段 第8课 SQL入门之使用数据处理函数 第9课 SQL入门之汇总数据 第…...

thinkphp6.0升级到8.0
目录 一:升级过程 二:报错处理 最近写的项目需要使用thinkphp8.0,之前的老项目需要从php6.0升级到8.0,特此记录下升级过程。 一:升级过程 查看版本: php think version,我目前的版本是6.1.4 生成thin…...
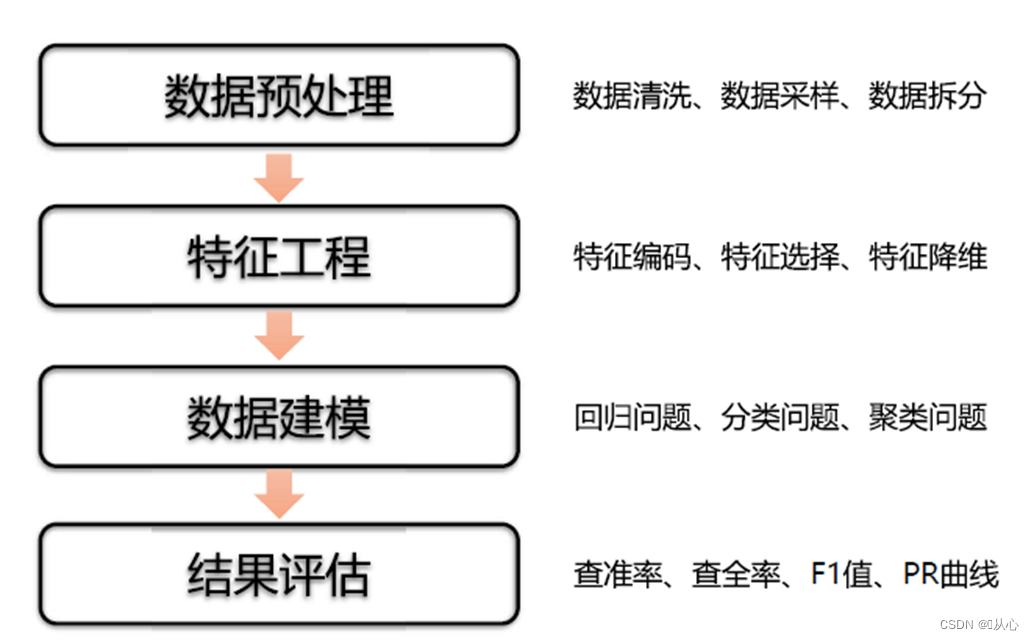
机器学习(一) -- 概述
系列文章目录 机器学习(一) -- 概述 机器学习(二) -- 数据预处理 未完待续…… 目录 系列文章目录 前言 一、机器学习定义(是什么) 二、机器学习的应用(能做什么) 三、***机器…...
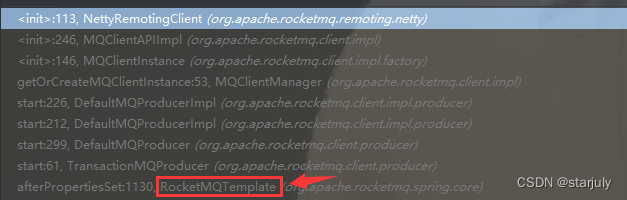
SpringBoot定时监听RocketMQ的NameServer
问题分析 自己在测试环境部署了RocketMQ,发现namesrv很容易挂掉,于是就想着监控,挂了就发邮件通知。查看了rocketmq-dashboard项目,发现只能监控Broker,遂放弃这一路径。于是就从报错的日志入手,发现最终可…...
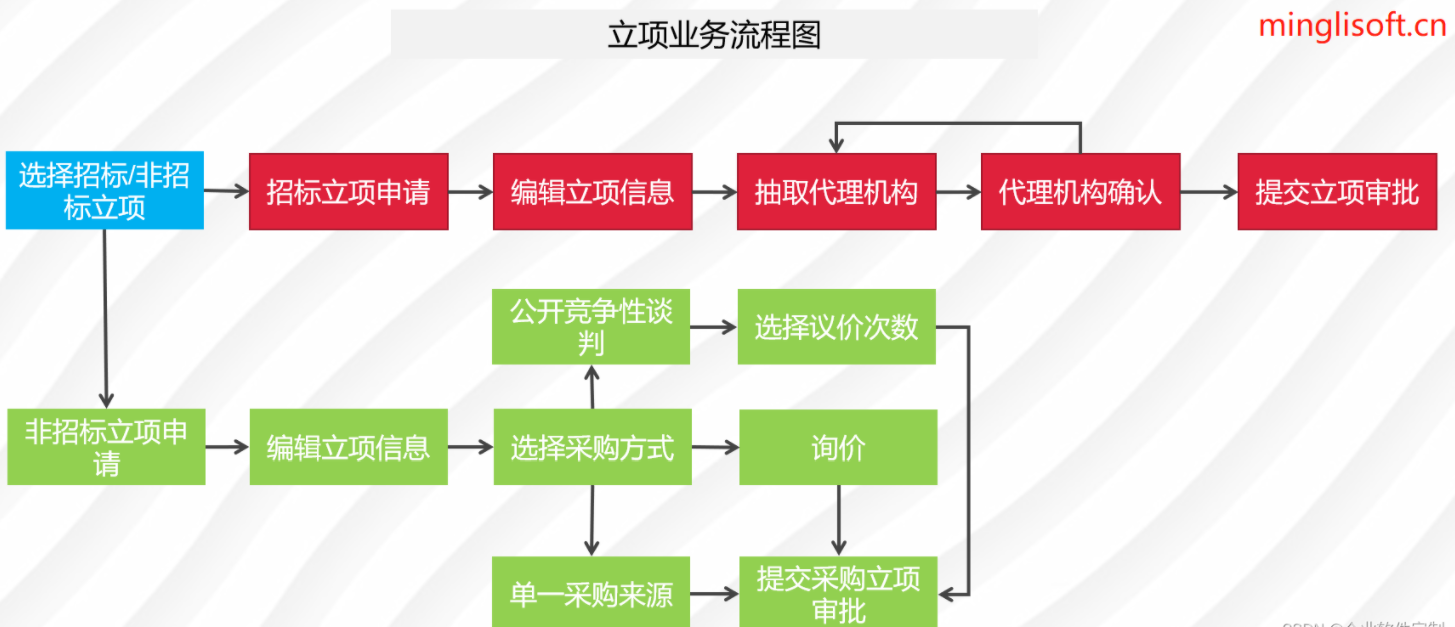
电子招标采购系统源码之从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理
在数字化时代,采购管理也正经历着前所未有的变革。全过程数字化采购管理成为了企业追求高效、透明和规范的关键。该系统通过Spring Cloud、Spring Boot2、Mybatis等先进技术,打造了从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通过…...

各部门请注意,VELO维乐潮流骑士尼莫出街啦,快来加入吧!
VELO潮流骑士丨车界“小学生”尼莫,下面是来自她的自诉: 大家好!我是尼莫,一枚骑车届的“小学生”,我爱上骑车已经有一年的时间啦!在这一年的时间里,骑车改变了我很多:爱上…...

Flutter配置Android和IOS允许http访问
默认情况下,Android和IOS只支持对https的访问,如果需要访问不安全的连接,也就是http,需要做以下配置。 Android 在res目录下的xml目录中(如果不存在,先创建xml目录),创建一个xml文件network_security_con…...

[设计模式 Go实现] 创建型~抽象工厂模式
抽象工厂模式用于生成产品族的工厂,所生成的对象是有关联的。 如果抽象工厂退化成生成的对象无关联则成为工厂函数模式。 比如本例子中使用RDB和XML存储订单信息,抽象工厂分别能生成相关的主订单信息和订单详情信息。 如果业务逻辑中需要替换使用的时候…...

移动端开发框架mui代码在安卓模拟器上运行(HbuilderX连接到模拟器)
开发工具 HBuilder X 3.8.12.20230817 注意:开发工具尽量用最新的或较新的。太旧的版本在开发调试过程中可能会出现莫名其妙的问题。 1、电脑下载安装安卓模拟器 我这里使用的是 夜神模拟器 ,也可以选择其他安卓模拟器 夜神模拟器官网:夜神安…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...
