数组--53.最大子数组和/medium
53.最大子数组和
- 1、题目
- 2、题目分析
- 3、解题步骤
- 4、复杂度最优解代码示例
- 5、抽象与扩展
1、题目
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
1 <= nums.length <= 105
-104 <= nums[i] <= 104
进阶:如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
2、题目分析
求连续子数组的最大和,意味着对数组切分成多段,此时有 2 个要点:
- 如何切分,什么情况下子数组还能接着往后连续下去?
求连续子数组的最大和,当子数组遇到新值时,
如果加该值,子数组的和大于该值,则让子数组继续往下遍历的效果更佳,
如果加该值,子数组的和小于该值,则不如让子数组在这做分割,然后下一个子数组从该新值开始。 - 对切分后的每一段数据做什么操作?
进行值的累加,并对比记录下各段子数组和的最大值。
3、解题步骤
- 初始化 2 个值:
a. 每段子数组的和=0
b. 各段子数组和的最大值max=数组首个元素(不能初始化为0,避免数组各段子数组和的最大值小于0的情况) - 遍历数组,并做 2 步:
a. sum = max(上个子数组 + 当前新值,当前新值)。即判断上个子数组是否还往下扩展,还是在此截止。
b. max = max(sum, max)。即max对比记录下各段子数组和的最大值。
4、复杂度最优解代码示例
public int maxSubArray(int[] nums) {int sum = 0;// 踩坑,这里不能初始化为 0。如当数组只有1个元素,且为负数时,max不会被替换为负数。int max = nums[0];for (int i = 0; i < nums.length; i++) {// a. sum = max(上个子数组 + 当前新值,当前新值)。即判断上个子数组是否还往下扩展,还是在此截止。sum = Math.max(sum + nums[i], nums[i]);// b. max = max(sum, max)。即max对比记录下各段子数组和的最大值。max = Math.max(sum, max);}return max;}
5、抽象与扩展
求连续子数组/子串的和值等问题,核心就是找到子数组/子串是否往下扩展的条件。
如本题中,
子数组要往下扩展的条件就是,子数组的和 + 新值 > 新值,则子数组接着往下扩展。
否则,新值 另起一个子数组。
相关文章:

数组--53.最大子数组和/medium
53.最大子数组和 1、题目2、题目分析3、解题步骤4、复杂度最优解代码示例5、抽象与扩展 1、题目 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连…...

centos 编译安装 python 和 openssl
安装环境: centos 7.9 : python 3.10.5 和 openssl 3.0.12 centos 6.10 : python 3.10.5 和 openssl 1.1.1 两个环境都能安装成功,可以正常使用。 安装 openssl 下载地址 下载后解压,进入到解压目录 执行…...
【nodejs】前后端身份认证
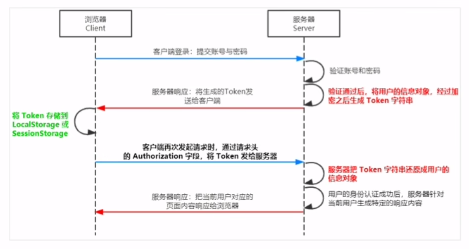
前后端身份认证 一、web开发模式 服务器渲染,前后端分离。 不同开发模式下的身份认证: 服务端渲染推荐使用Session认证机制前后端分离推荐使用JWT认证机制 二、session认证机制 1.HTTP协议的无状态性 了解HTTP协议的无状态性是进一步学习Session认…...

数据结构【线性表篇】(三)
数据结构【线性表篇】(三) 文章目录 数据结构【线性表篇】(三)前言为什么突然想学算法了?为什么选择码蹄集作为刷题软件? 目录一、双链表二、循环链表三、静态链表 结语 前言 为什么突然想学算法了? > 用较为“官方…...
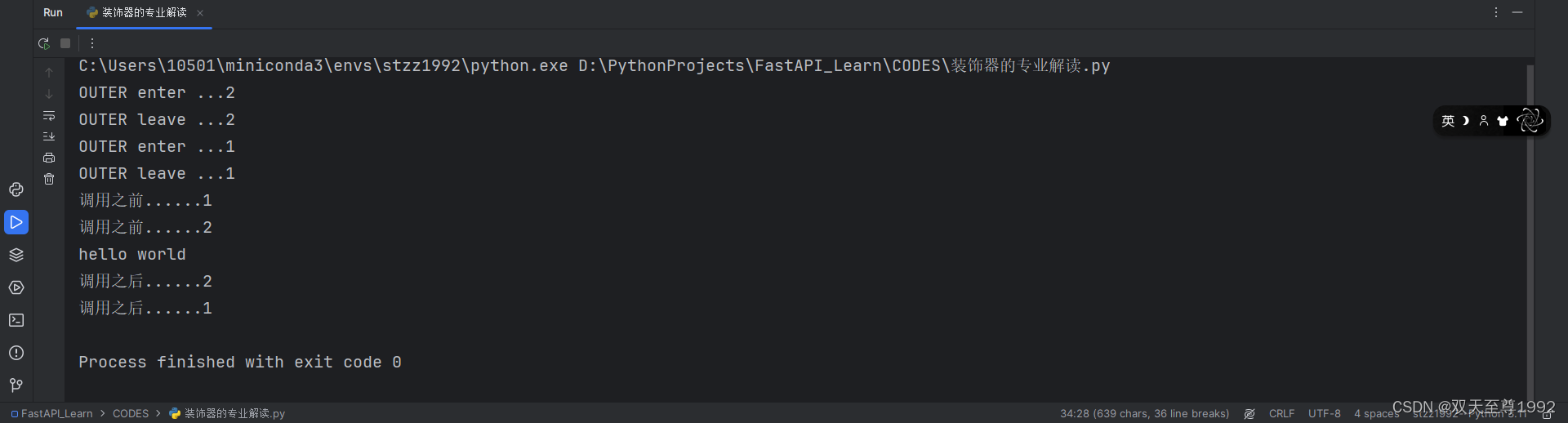
Python装饰器的专业解释
装饰器,其实是用到了闭包的原理来进行操作的。 单个装饰器: 以下是一个简单的例子: def outer(func):print("OUTER enter ...")def wrapper(*args, **kwargs):print("调用之前......")result func(*args, **kwargs)p…...
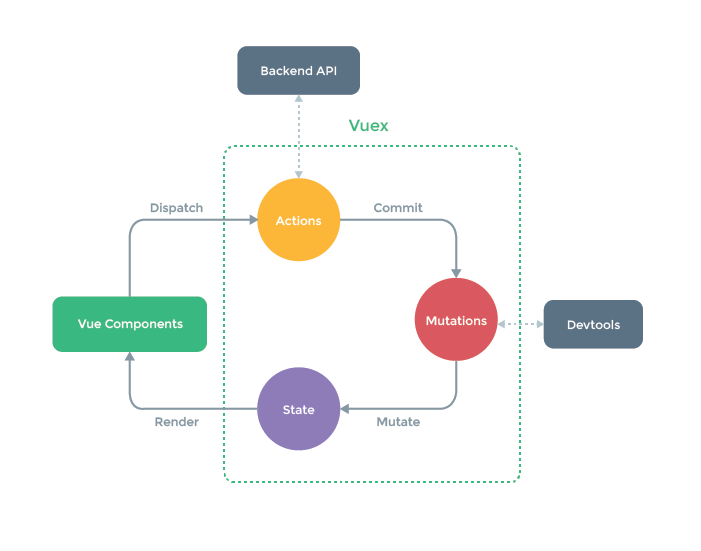
vue3框架笔记
Vue Vue 是一个渐进式的前端开发框架,很容易上手。Vue 目前的版本是 3.x,但是公司中也有很多使用的是 Vue2。Vue3 的 API 可以向下兼容 2,Vue3 中新增了很多新的写法。我们课程主要以 Vue3 为主 官网 我们学习 Vue 需要转变思想࿰…...
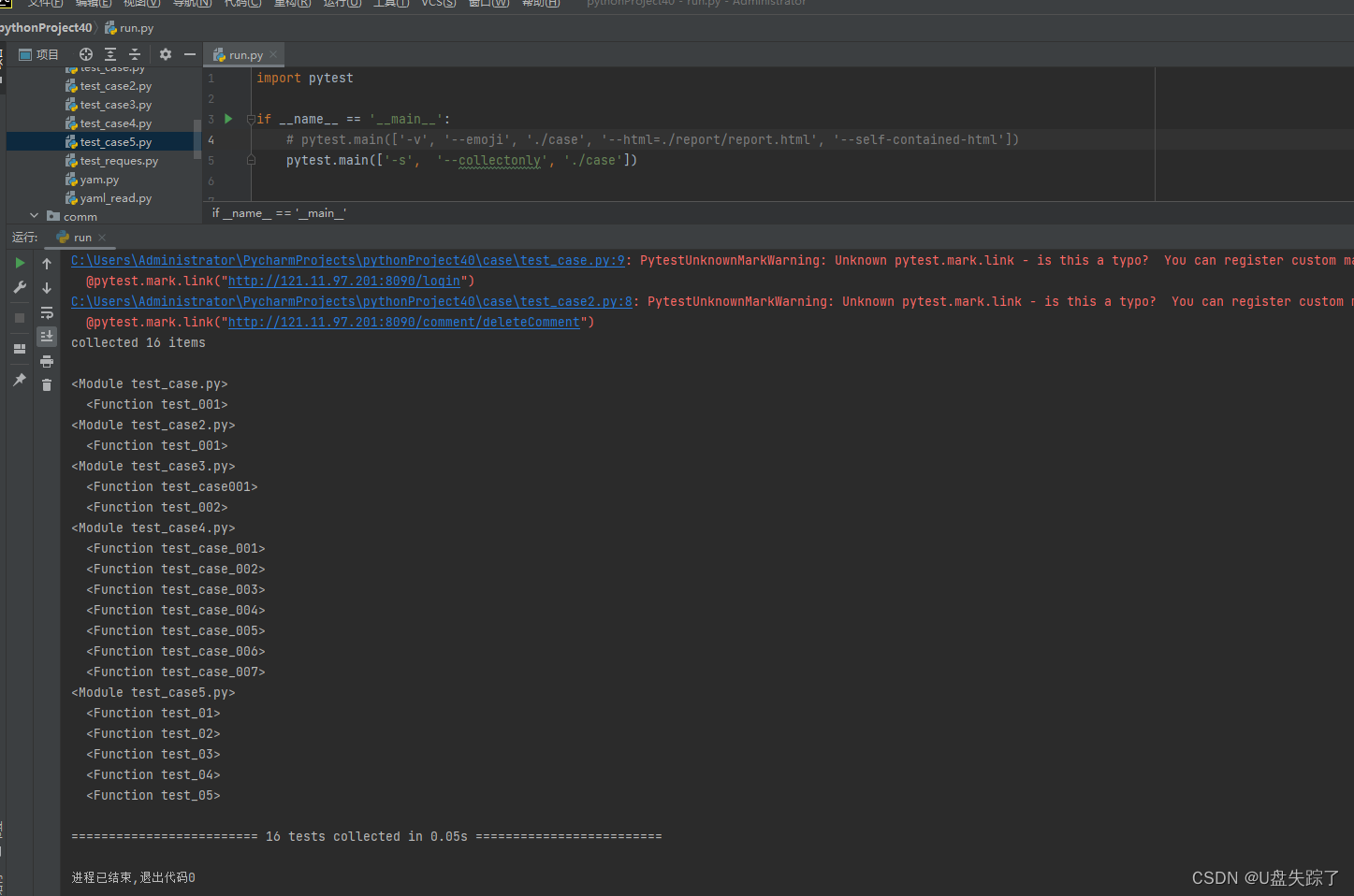
pytest --collectonly 收集测试案例
pytest --collectonly 是一条命令行指令,用于在运行 pytest 测试时仅收集测试项而不执行它们。它会显示出所有可用的测试项列表,包括测试模块、测试类和测试函数,但不会执行任何实际的测试代码。 这个命令对于查看项目中的测试结构和确保所有…...
dev express 15.2图表绘制性能问题(dotnet绘图表)
dev express 15.2 绘制曲线 前端代码 <dxc:ChartControl Grid.Row"1"><dxc:XYDiagram2D EnableAxisXNavigation"True"><dxc:LineSeries2D x:Name"series" CrosshairLabelPattern"{}{A} : {V:F2}"/></dxc:XYDi…...

WorkPlus:领先的IM即时通讯软件,打造高效沟通协作新时代
在当今快节奏的商业环境中,高效沟通和协作是企业成功的关键。而IM即时通讯软件作为实现高效沟通的利器,成为了现代企业不可或缺的一部分。作为一款领先的IM即时通讯软件,WorkPlus以其卓越的性能和独特的功能,助力企业打造高效沟通…...
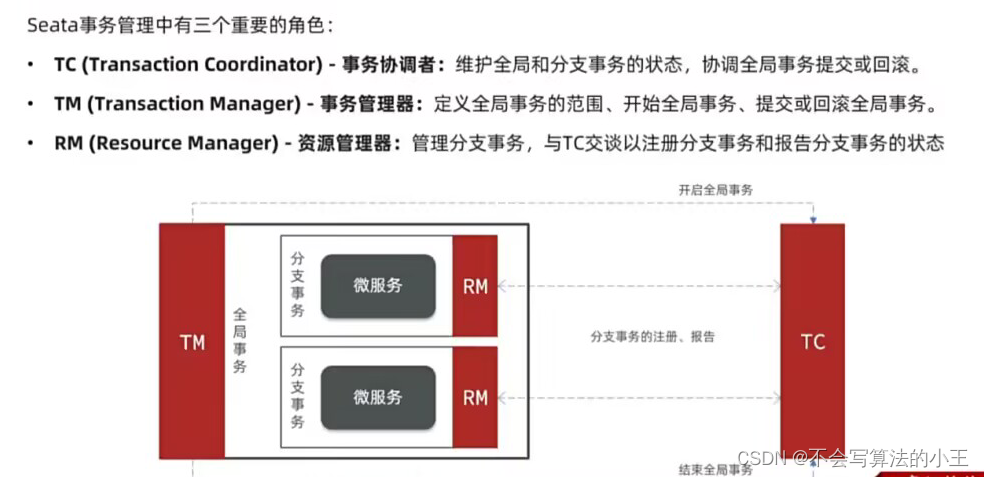
学习SpringCloud微服务
SpringCloud 微服务单体框架微服务框架SpringCloud微服务拆分微服务差分原则拆分商品服务拆分购物车服务拆分用户服务拆分交易服务拆分支付服务服务调用RestTemplate远程调用 微服务拆分总结 服务治理注册中心Nacos注册中心服务注册服务发现 OpenFeign实现远程调用快速入门引入…...
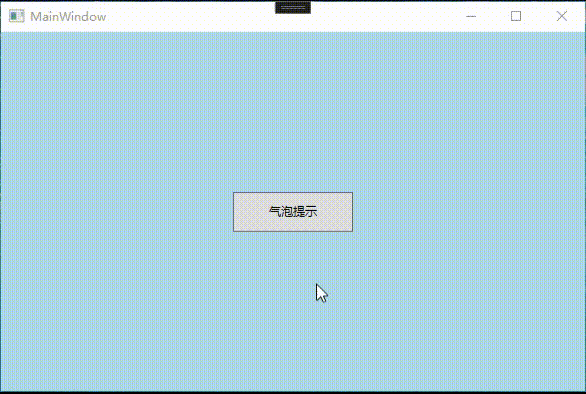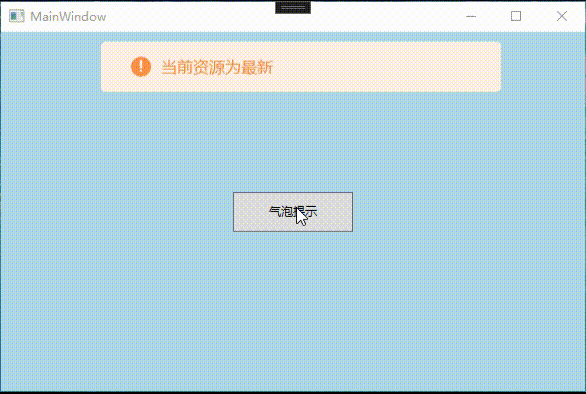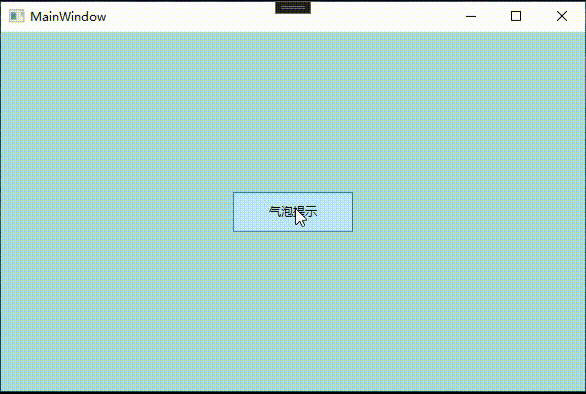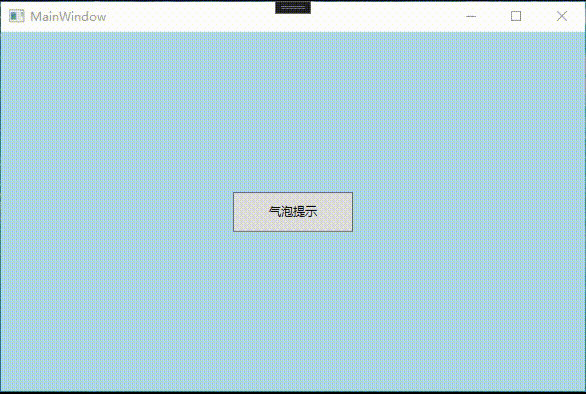
WPF 显示气泡提示框
气泡提示框应用举例 有时候在我们开发的软件经常会遇到需要提示用户的地方,为了让用户更直观,快速了解提示信息,使用简洁、好看又方便的气泡提示框显得更加方便,更具人性化。如下面例子:(当用户未输入账号时࿰…...
L1-062:幸运彩票
题目描述 彩票的号码有 6 位数字,若一张彩票的前 3 位上的数之和等于后 3 位上的数之和,则称这张彩票是幸运的。本题就请你判断给定的彩票是不是幸运的。 输入格式: 输入在第一行中给出一个正整数 N(≤ 100)。随后 N 行…...

python+vue高校体育器材管理信息系统5us4g
优秀的高校体育馆场地预订系统能够更有效管理体育馆场地预订业务规范,帮助管理者更加有效管理场地的使用,有效提高场地使用效率,可以帮助提高克服人工管理带来的错误等不利因素,所以一个优秀的高校体育馆场地预订系统能够带来很大…...
10 款顶级的免费U盘数据恢复软件(2024 年 更新)
你曾经遇到过U盘无法访问的情况吗?现在我们教你如何恢复数据。 在信息时代,数据丢失往往会造成巨大的困扰。而USB闪存驱动器作为我们常用的数据存储设备,其重要性不言而喻。但是,U盘也可能会出现各种问题,如无法访问、…...

C# json 转匿名对象及C#关键字的处理
调用第三方接口,返回的json字符串,为了方便使用转为C#匿名对象: /// <summary>/// json转为匿名对象/// </summary>/// <typeparam name"T"></typeparam>/// <param name"json"></para…...

关于彻底通过外网,自动批量下载Python的pip依赖包后到企业内网重安装的步骤-比单个包的要方便多了。
关于彻底通过外网,自动批量下载Python包后到企业内网重安装的步骤 前言: 哎,在本人的前面的博客中,分享的方法可能是不通用的。因为在一次实践中发现它不能总是通用且麻烦。所以本次记录分享一个更方便快速的方式。 上期前言&am…...

Oracle T4-4小型机上配置Ldom部署rac
Ldom控制域配置 (两台主机一样,以hydb1为例) roothydb1 # ldm add-vds primary-vds0 primary roothydb1 # ldm add-vcc port-range5000-5100 primary-vcc0 primary roothydb1 # ldm add-vsw net-devigb0 primary-vsw0 primary roothydb1 # ldm add-vsw net-devixgbe…...

【2023Hadoop大数据技术应用期末复习】填空题题型整理
大数据的 4V 特征包含()()()() 答案:大量、多样、高速、价值Hadoop 三大组件包含()()() 答案&…...
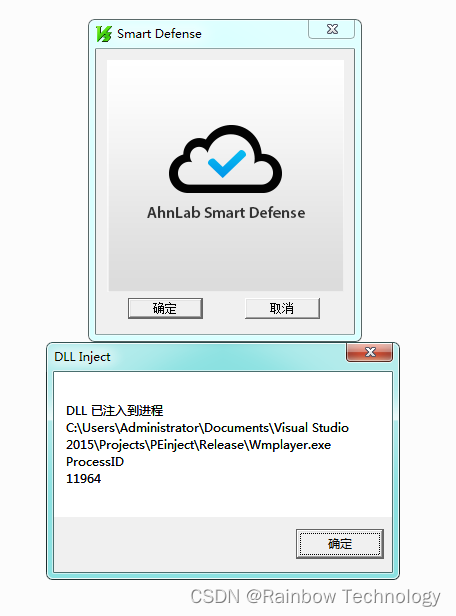
劫持 PE 文件:新建节表并插入指定 DLL 文件
PE格式简介 PE(Portable Executable)格式,是微软Win32环境可移植可执行文件(如exe、dll、vxd、sys和vdm等)的标准文件格式。PE格式衍生于早期建立在VAX(R)VMS(R)上的COFF(Common Object File Format)文件格式。 Portable 是指对于不同的Windows版本和不同的CPU类型上…...
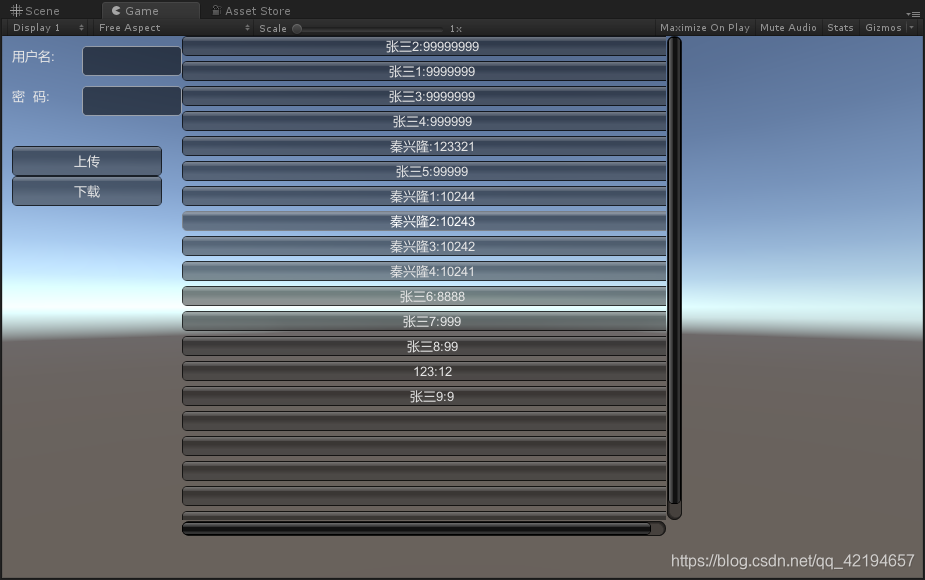
HTTP分数排行榜
HTTP分数排行榜 介绍一、创建数据库二、创建PHP脚本三、上传下载分数四、测试 介绍 Unity中向服务器发送用户名和得分,并存入数据库,再讲数据库中的得分按照降序的方式下载到Unity中。 一、创建数据库 首先,我们要在MySQL数据库中建立一个…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...
