机器人中的数值优化之线性共轭梯度法
欢迎大家关注我的B站:
偷吃薯片的Zheng同学的个人空间-偷吃薯片的Zheng同学个人主页-哔哩哔哩视频 (bilibili.com)
本文ppt来自深蓝学院《机器人中的数值优化》
目录
1.无约束优化方法对比
2.Hessian-vec product
3.线性共轭梯度方法的步长编辑
4.共轭梯度方向的求解
5.线性共轭梯度方法整体流程
1.无约束优化方法对比

拟牛顿方法和牛顿共轭梯度方法是最优的,实现收敛速率与iteration work之间的平衡
2.Hessian-vec product

hessian矩阵需要n方的复杂度,逆需要n三次方的复杂度,我们求解d需要hessian矩阵的逆
hessian与向量的乘积经过泰勒展开的简化可以变为只需求两次梯度
3.线性共轭梯度方法的步长
A应该也是未知的,我们只能输入x得到Ax的值

求解线性方程这个任务转化为求二次函数的最小值
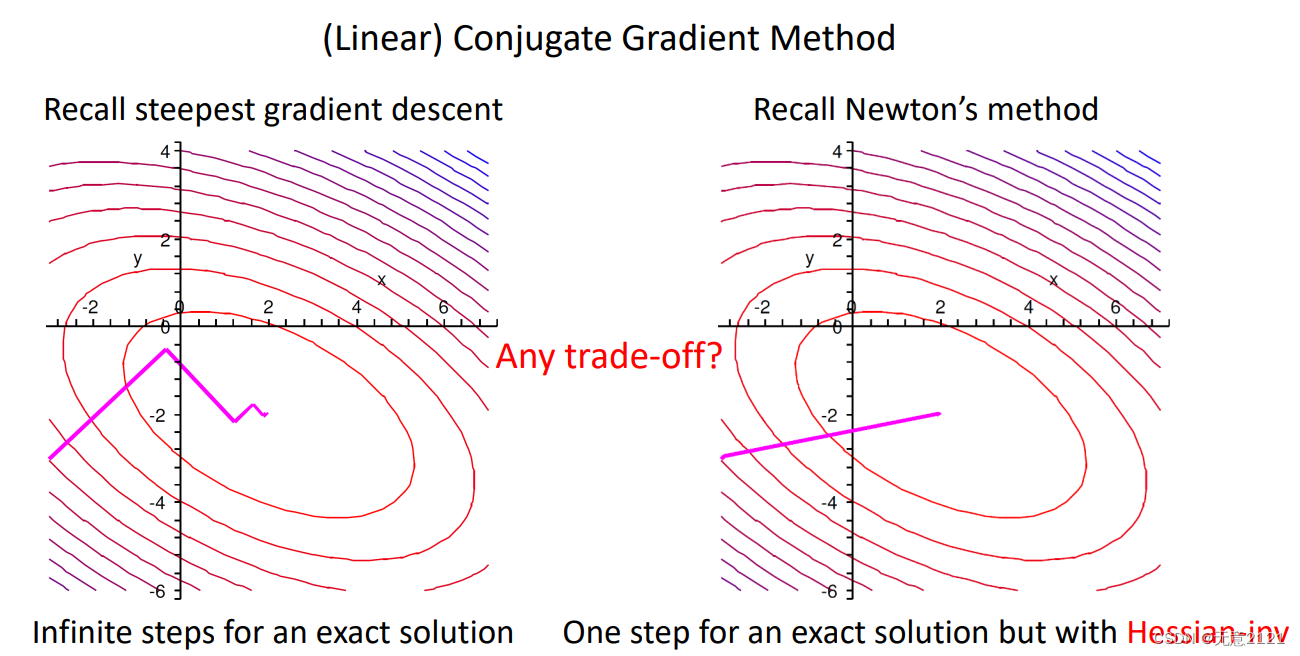
最速下降法收敛比较慢
牛顿方法需要涉及Hessian求逆

如果A=I,那么等高线是圆,n维则是对应超球,但是每次的迭代都是相互垂直的,只要n步这样正交的方向迭代搜索就能获得精确的最小值
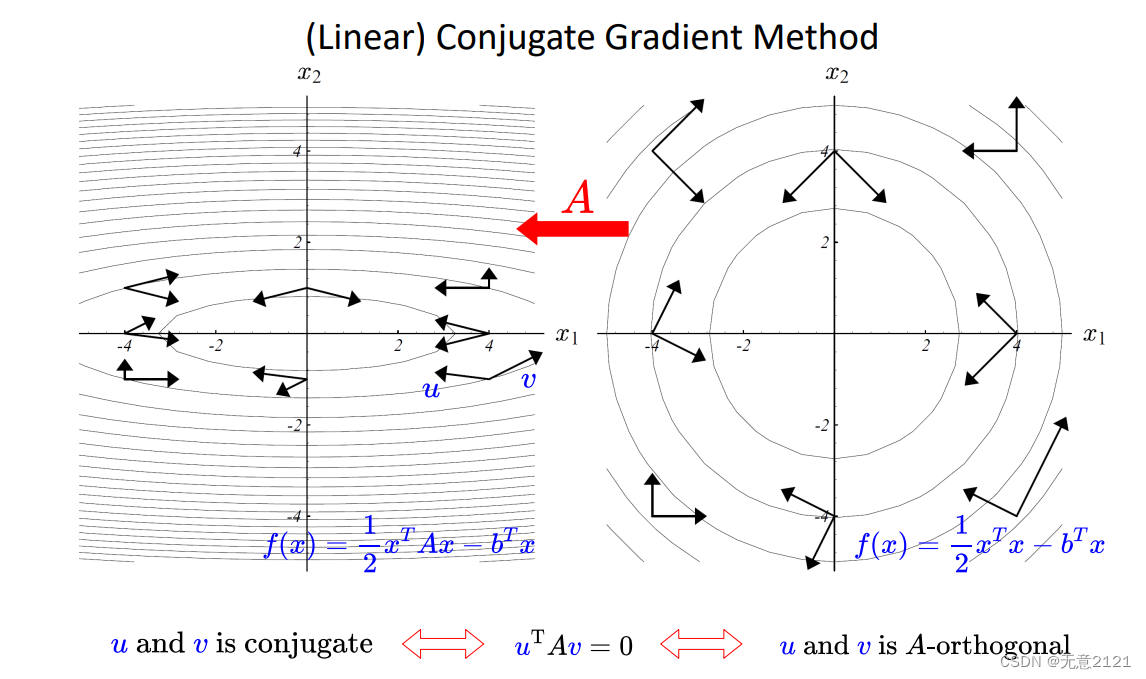
对于A!=I时,等高线为椭球,相当于做了仿射变换,原来的正交,现在则是共轭,定义如上

这里对步长进行求导则可以得到步长的闭式解,并且由其形式可看出我们只需要知道Ax这样输入x得出Ax的值的接口就行
4.共轭梯度方向的求解

施密特正交化就是不断把基底方向的分量减掉,剩下的就是和已经存在的基底正交的另一个基底
共轭的施密特正交化与一般的施密特正交化的区别就是内积中间有系数矩阵A
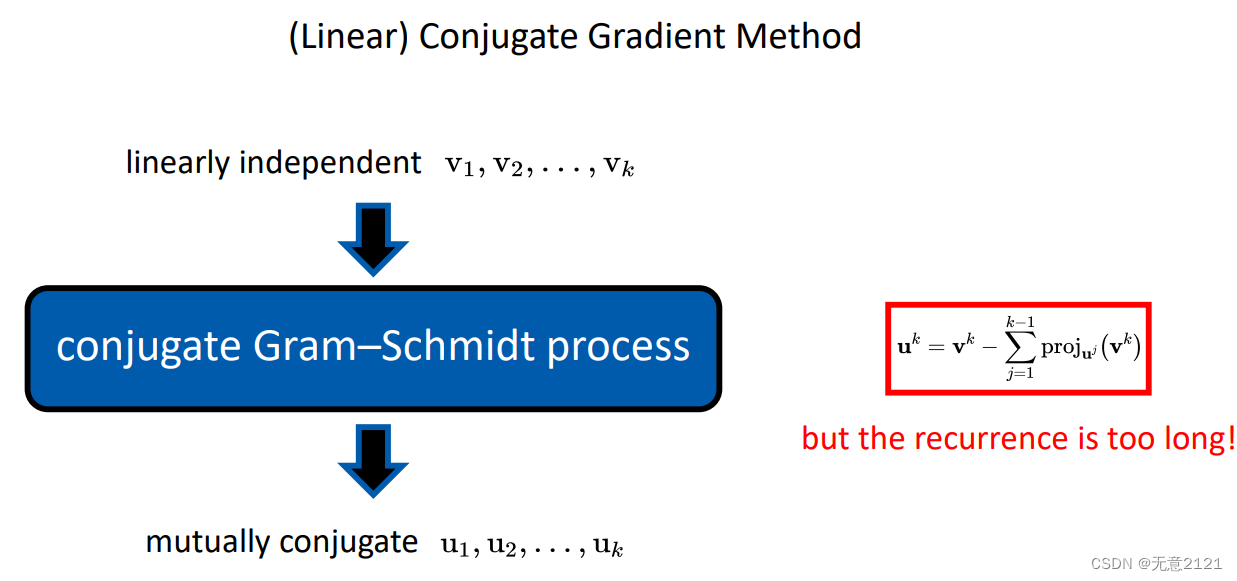

按部就班来还是k方的复杂度,实际上可以增量式地计算
这里令每一次Vk是残差,但这个残差已经把在之前的共轭投影上都是零了
5.线性共轭梯度方法整体流程

相关文章:

机器人中的数值优化之线性共轭梯度法
欢迎大家关注我的B站: 偷吃薯片的Zheng同学的个人空间-偷吃薯片的Zheng同学个人主页-哔哩哔哩视频 (bilibili.com) 本文ppt来自深蓝学院《机器人中的数值优化》 目录 1.无约束优化方法对比 2.Hessian-vec product 3.线性共轭梯度方法的步长编辑 4.共轭梯度…...

嵌入式Linux C语言介绍
目录 一.前言 二.C语言的特点 一.前言 开发工具通常依赖于操作系统提供的各种功能和服务。许多开发工具都基于操作系统的API(应用程序接口)进行开发,这些API提供了文件处理、网络通信、图形界面等核心功能。没有操作系统的支持,…...

基于Java电影院票票务系统
基于Java电影院票票务系统 功能需求 1、用户登录与注册:用户可以通过系统注册账号并登录系统,方便进行购票和管理个人信息。 2、个人信息管理:用户可以查看和修改个人信息,包括姓名、联系方式等。 3、影片信息查询:…...

HarmonyOS应用开发实战—开箱即用的登录页面3【ArkTS】
文章目录 一.HarmonyOS应用开发实战—开箱即用的登录页面2【ArkTS】【鸿蒙专栏-31】1.1 项目背景1.2 ArkTS详解二.HarmonyOS应用开发实战—开箱即用的登录页面3【ArkTS】2.1 ArkTS页面源码2.2 代码解析2.3 心得一.HarmonyOS应用开发实战—开箱即用的登录页面2【ArkTS】【鸿蒙专…...

Unity坦克大战开发全流程——1)需求分析
实践项目:需求分析 该游戏共有三个主要部分:UI、数据储存、核心游戏逻辑,下面我们将从开始场景、游戏场景、结束场景三个角度切入进行分析。...

python练习2【题解///考点列出///错题改正】
一、单选题 【文件】 *1.【单选题】 ——文件:读取方法 下列哪个选项可以从文件中读取任意字节的内容?(C )A A.read() B.readline() C.readlines() D.以上全部 A\B\C三种方法都是可以读取文件中任意的字节内容的࿰…...
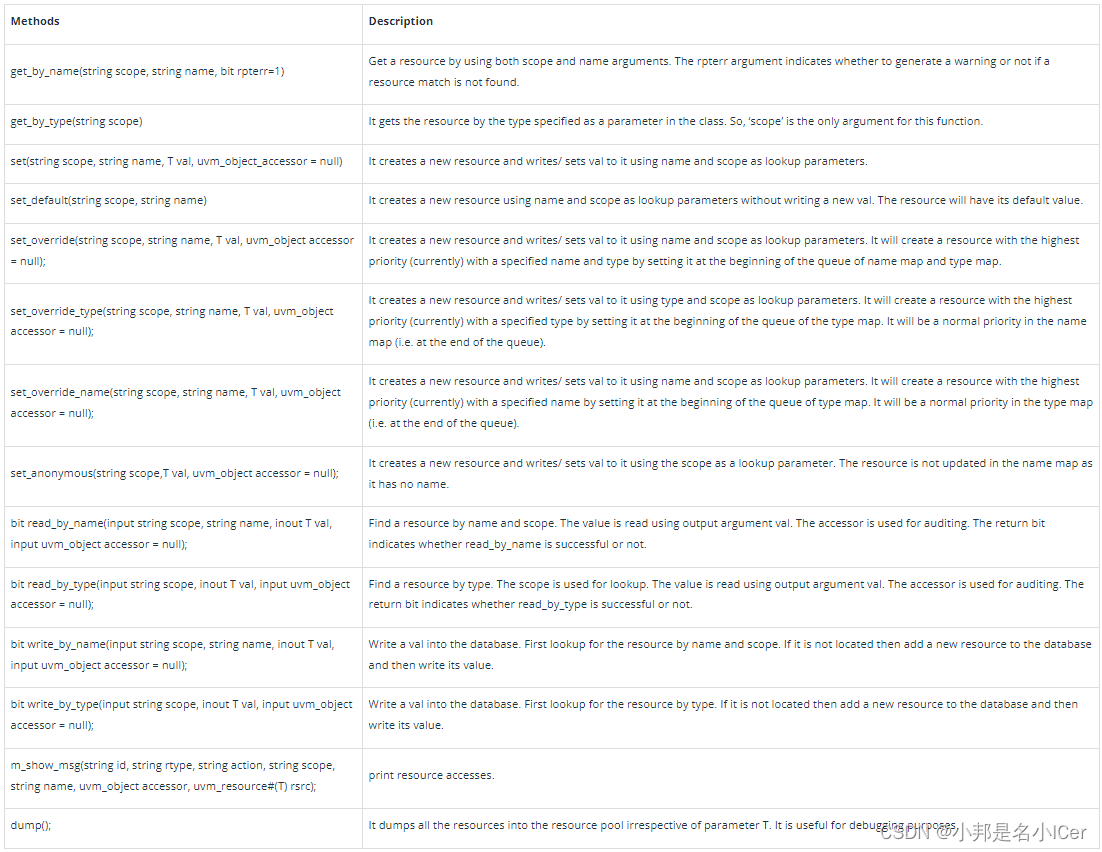
7.2 uvm_resource_db in UVM
uvm_resource_db是一个类型参数化 type-parameterized的类,它是资源数据库顶部的一个方便层(convenience layer)。这个便利层简化了对低级数据库的访问,并且没有添加新功能。因此,uvm_resource_db不是从uvm_resource类派生的。以下uvm_resour…...
)
洛谷——P3879 [TJOI2010] 阅读理解(STL:hash+set,c++)
文章目录 一、题目[TJOI2010] 阅读理解题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示 二、题解基本思路:代码 一、题目 [TJOI2010] 阅读理解 题目描述 英语老师留了 N N N 篇阅读理解作业,但是每篇英文短文都有很多生词需要查字典&am…...
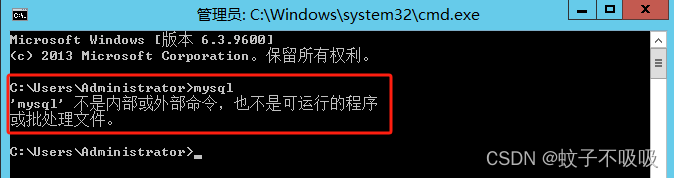
Windows/Linux环境登入mysql、mysqldump命令等多方式解决方案之简易记录
Windows/Linux环境登入mysql、mysqldump命令等多方式解决方案之简易记录 之前发布过Window方式,这次结合以上主题,完善下Linux相关登入方式过程,纯属做个记录,有需要的朋友可以做个学习参考。 一、Windows环境提示“‘mysql’ 不是内部或外部命令,也不是可运行的程序或批…...

【基础】【Python网络爬虫】【13.免费代理与付费代理】(附大量案例代码)(建议收藏)
Python网络爬虫基础 一、免费代理1. 什么是代理IP2. 代理IP的类型3. 代理IP的作用4. 免费代理的潜在风险5. 免费代理网站 二、付费代理1. 找付费代理服务站点2. 生成获取代理的api接口3. python获取代理请求接口示例数据返回示例 4. 解决请求速率5. 品易代理使用注意事项代理添…...

【 YOLOv5】目标检测 YOLOv5 开源代码项目调试与讲解实战(3)-训练yolov5模型(本地)
训练yolov5模型(本地) 训练文件 train.py训练如下图 一些参数的设置weights:对于weight参数,可以往Default参数中填入的参数有 cfg:(缩写)cfg参数可以选择的网络模型 data对于data hyp 超参数epochs 训练多…...
fastApi 项目部署
方式一,Uvicorn部署 Run a Server Manually - Uvicorn - FastAPI 1,linux服务器安装 python>3.8 2,安装 uvicorn : pip install "uvicorn[standard]" 3,上传项目到服务器 main.py from typing imp…...

python操作mysql数据库
说明:这里仅仅为了演示python操作MySQL数据库,真实环境中,最好把CURD分别封装为对应的方法。并将这些方法在类中封装,体现python面向对象的特征。python链接MySQL数据库 建表 create database mydb; use mydb; create table EMP…...
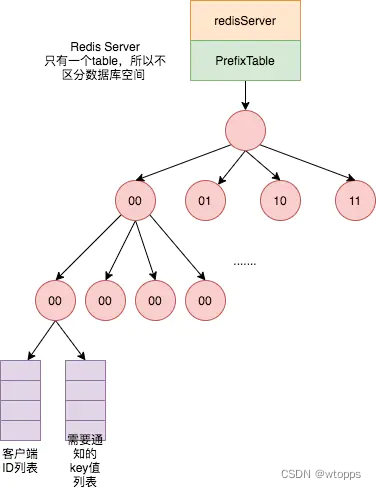
Redis6.0 Client-Side缓存是什么
前言 Redis在其6.0版本中加入了Client-side caching的支持,开启该功能后,Redis可以将指定的key-value缓存在客户端侧,这样当客户端发起请求时,如果客户端侧存在缓存,则无需请求Redis Server端。 Why Client-side Cac…...
Leetcode—1572.矩阵对角线元素的和【简单】
2023每日刷题(七十三) Leetcode—1572.矩阵对角线元素的和 实现代码 class Solution { public:int diagonalSum(vector<vector<int>>& mat) {int n mat.size();if(n 1) {return mat[0][0];}int sum 0;int i 0, j n - 1;while(i &…...

基于SpringBoot的二手手机商城系统的设计与实现
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的二手手机商城系统的设计…...

OpenFeign相关面试题及答案
1、什么是OpenFeign,它如何简化远程服务调用? OpenFeign是一个声明式的Web服务客户端,它使得编写HTTP客户端变得更加容易。它属于Spring Cloud Netflix项目的一部分,可以与Spring Boot应用轻松集成。通过使用OpenFeign࿰…...
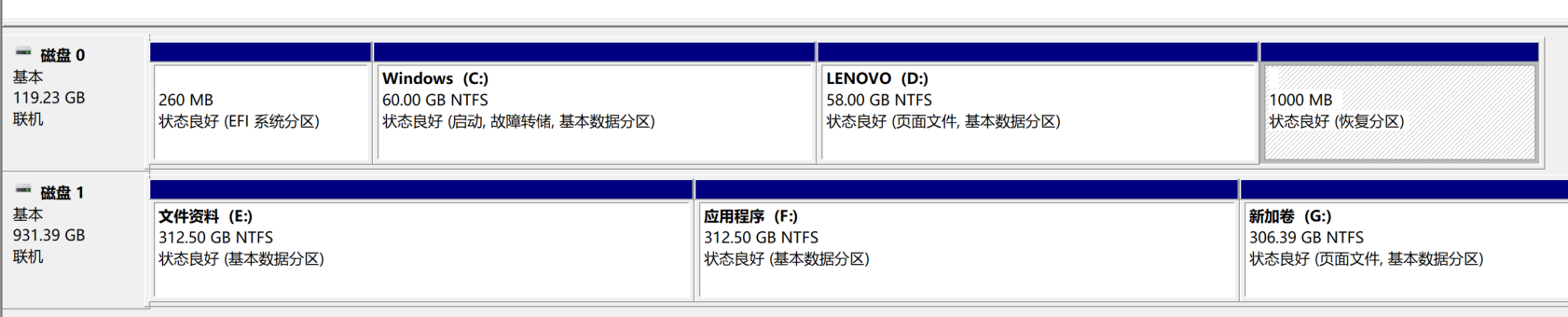
c盘扩容时,d盘无法删除卷问题
C盘扩容时,磁盘管理中D盘右键无法删除卷的原因 首先,D盘下文件夹为空,但是显示可用空间不是100%,经过排查,发现是虚拟内存设置在了D盘导致无法删除卷,这里只需要将虚拟内存放到其他盘,如E盘即可…...
)
NumPy 中级教程——广播(Broadcasting)
Python NumPy 中级教程:广播(Broadcasting) 在 NumPy 中,广播是一种强大的机制,它允许不同形状的数组在进行操作时,自动进行形状的调整,使得它们能够完成一致的运算。广播使得对数组的操作更加…...
python-39-flask+nginx+Gunicorn的组合应用
flask nginx Gunicorn 王炸 1 flasknginxgunicornsupervisor 1.1 myapp.py from flask import Flask app Flask(__name__)app.route("/") def test_link():return "the link is very good"if __name__"__main__":app.run()默认是5000端口…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
