算法专题四:前缀和
前缀和
- 一.一维前缀和(模板):
- 1.思路一:暴力解法
- 2.思路二:前缀和思路
- 二. 二维前缀和(模板):
- 1.思路一:构造前缀和数组
- 三.寻找数组的中心下标:
- 1.思路一:前缀和
- 四.除自身以外数组的乘积:
- 1.思路一:暴力解法
- 2.思路二:前缀积+后缀积
- 五.和为K的子数组:
- 1.思路一:前缀和+哈希
- 六.前缀和可以被K整除的子数组:
- 1.思路一:前缀和+哈希
- 七.连续数组:
- 1.思路一:
- 八.矩阵区域和:
- 1.思路一:二维前缀和模板+细节处理
一.一维前缀和(模板):

一维前缀和
1.思路一:暴力解法
1.输入数组长度n和查询次数q。
2.使用一个一维数组保存数据。
3.使用一个循环获取q次需要查询范围的数据。
4.遍历r-l+1次进行一个范围求和然后输出。
5.时间复杂度:O(n^2)
6.通过不了所有的测试用例。
2.思路二:前缀和思路
1.输入数组长度n和查询次数q。
2.使用一个一维数组保存数据。
3.构建一个前缀和的一个数组。
4.使用一个循环获取q次需要查询范围的数据。
5.时间复杂度:O(n^2)
6.通过不了所有的测试用例。
#include <iostream>
#include <vector>
using namespace std;int main()
{//1.输入数组长度和查询次数: int n =0,q=0;cin>>n>>q;//2.输入数组数据:vector<int> arr(n+1);for(int i=1;i<=n;i++) cin>>arr[i];//3.前缀和数组:vector<long long> bp(n+1);for(int i=1;i<=n;i++) bp[i] = bp[i-1] + arr[i];//4.计算和:int i=0,r=0;while(q!=0){cin>>i>>r;cout<<(bp[r] - bp[i-1])<<endl;q--;}
}
二. 二维前缀和(模板):

二维前缀和
1.思路一:构造前缀和数组
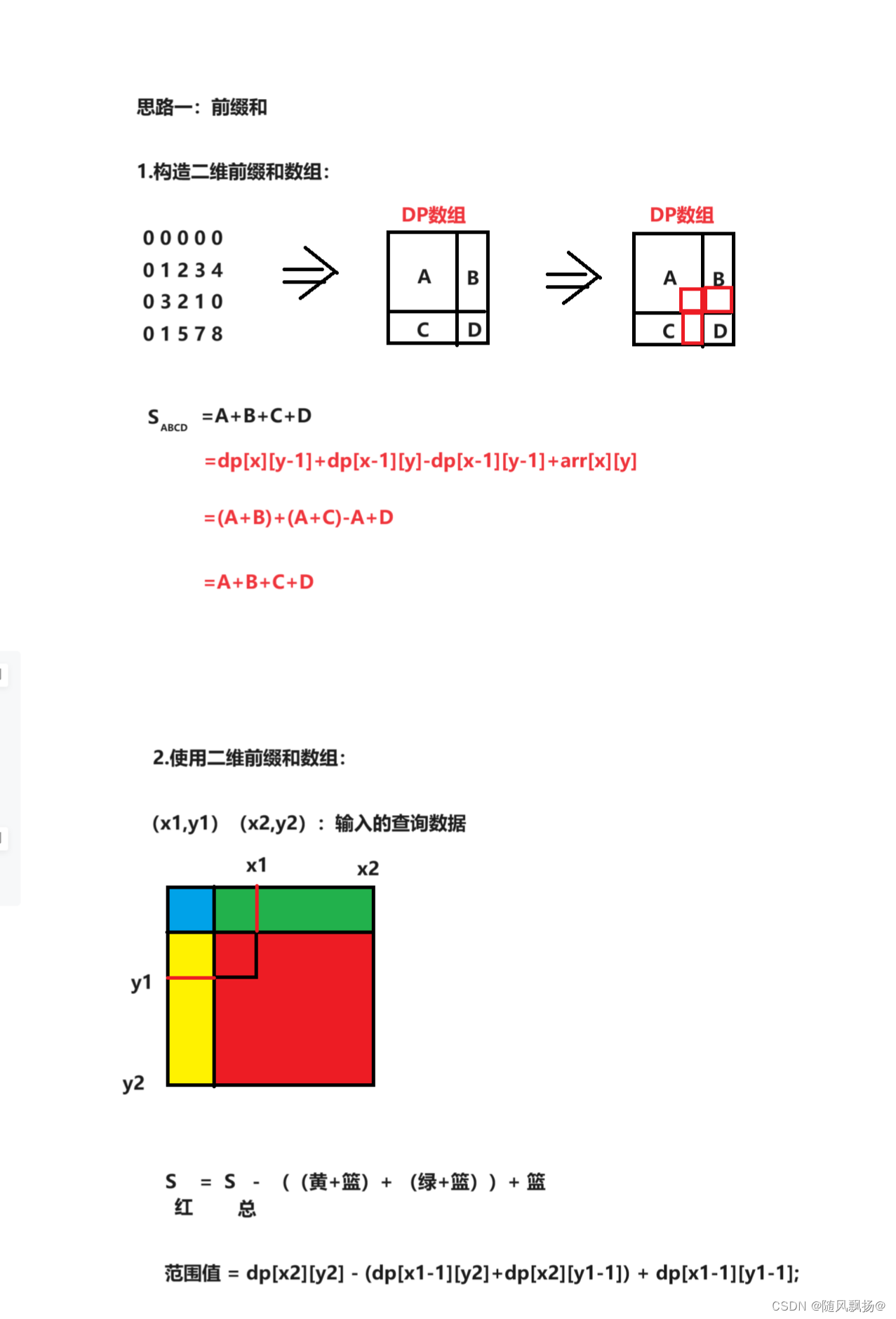
#include <iostream>
#include <vector>
using namespace std;int main()
{//1.n行m列的一个二维数组:int n = 0, m = 0, q = 0;cin >> n >> m >> q;//2.数组输入数据:vector<vector<int>> vv((n + 1),vector<int>(m+1));for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++)cin >> vv[i][j];}//3.创造二维的求和dp数组vector<vector<long long>> dp((n + 1), vector<long long>(m + 1));for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){dp[i][j] = ((dp[i][j - 1] + dp[i - 1][j]) - dp[i-1][j-1]) + vv[i][j];}}//4.数据查询:while (q != 0){int x1 = 0, y1 = 0, x2 = 0, y2 = 0;cin >> x1 >> y1 >> x2 >> y2;cout << (dp[x2][y2] - (dp[x1 - 1][y2] + dp[x2][y1-1]) + dp[x1-1][y1-1]) << endl;q--;}}
三.寻找数组的中心下标:

寻找数组的中心下标
1.思路一:前缀和

class Solution {
public:int pivotIndex(vector<int>& nums) {//1.构建前缀和数组:int n = nums.size();vector<int> dp(n+1);//2.前缀和数组值遍历:for(int i = 1 ; i<=n;i++) dp[i] = dp[i-1] + nums[i-1];//3.进行中心下标的寻找:int mid = -1;for(int i=1 ; i <= n ; i++){if((dp[i-1] - dp[0]) == (dp[n] - dp[i])){mid = i-1;break;}}//4.没有中心下标的情况:return (mid == -1? -1:mid);}
};
四.除自身以外数组的乘积:

除自身以外数组的乘积
1.思路一:暴力解法
2.思路二:前缀积+后缀积
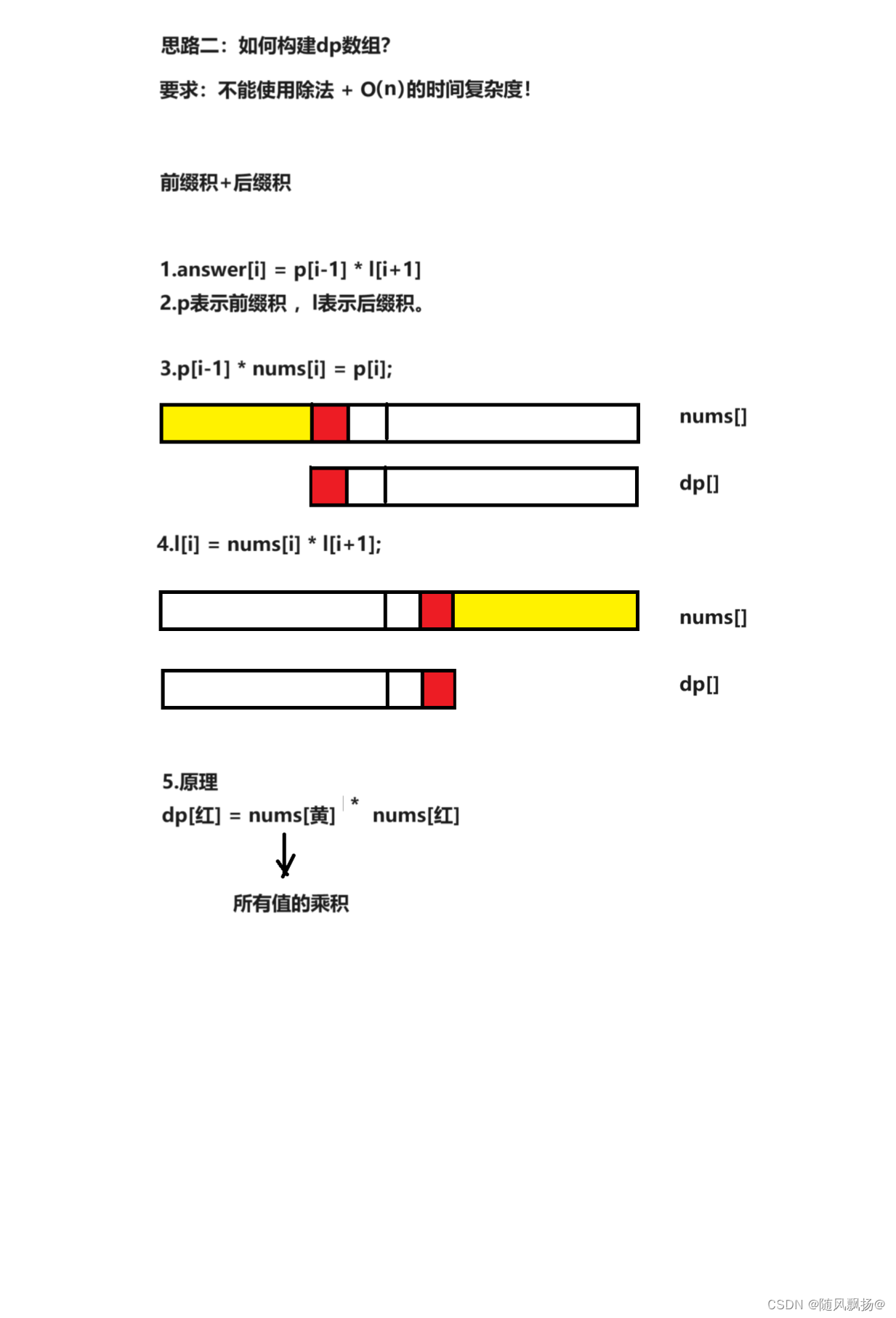
class Solution {
public:vector<int> productExceptSelf(vector<int>& nums) {//1.前缀积+后缀积int n = nums.size();vector<int> left(n + 1, 1);vector<int> right(n + 1, 1);//2.遍历确定前缀积+后缀积的值:for (int i = 1; i <= n; i++) left[i] = left[i - 1] * nums[i - 1];for (int i = n - 1; i >= 0; i--) right[i] = right[i + 1] * nums[i];// 1 1 2 6 24// 24 24 12 4 1// 0 1 2 3 4//0 1 2 3//24 12 8 6vector<int> ret(n);//3.遍历ret数组并且赋值for (int i = 0; i < n; i++){ret[i] = left[i] * right[i+1];}return ret;}
};
五.和为K的子数组:

和为K的子数组
1.思路一:前缀和+哈希

class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int,int> hash;hash[0]=1;int sum = 0 , ret = 0;for(auto n : nums){sum+=n;if(hash.count(sum-k)) ret+=hash[sum-k];hash[sum]++;}return ret;}
};
六.前缀和可以被K整除的子数组:

前缀和可以被K整除的子数组
1.思路一:前缀和+哈希

class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int,int> hash;hash[0] = 1;//1.开始遍历+判断int sum = 0 , ret = 0;for(auto a : nums){sum+=a;int n = (sum%k + k) % k;if(hash.count(n)) ret+=hash[n];hash[n]++;}return ret;}
};
七.连续数组:

连续数组
1.思路一:

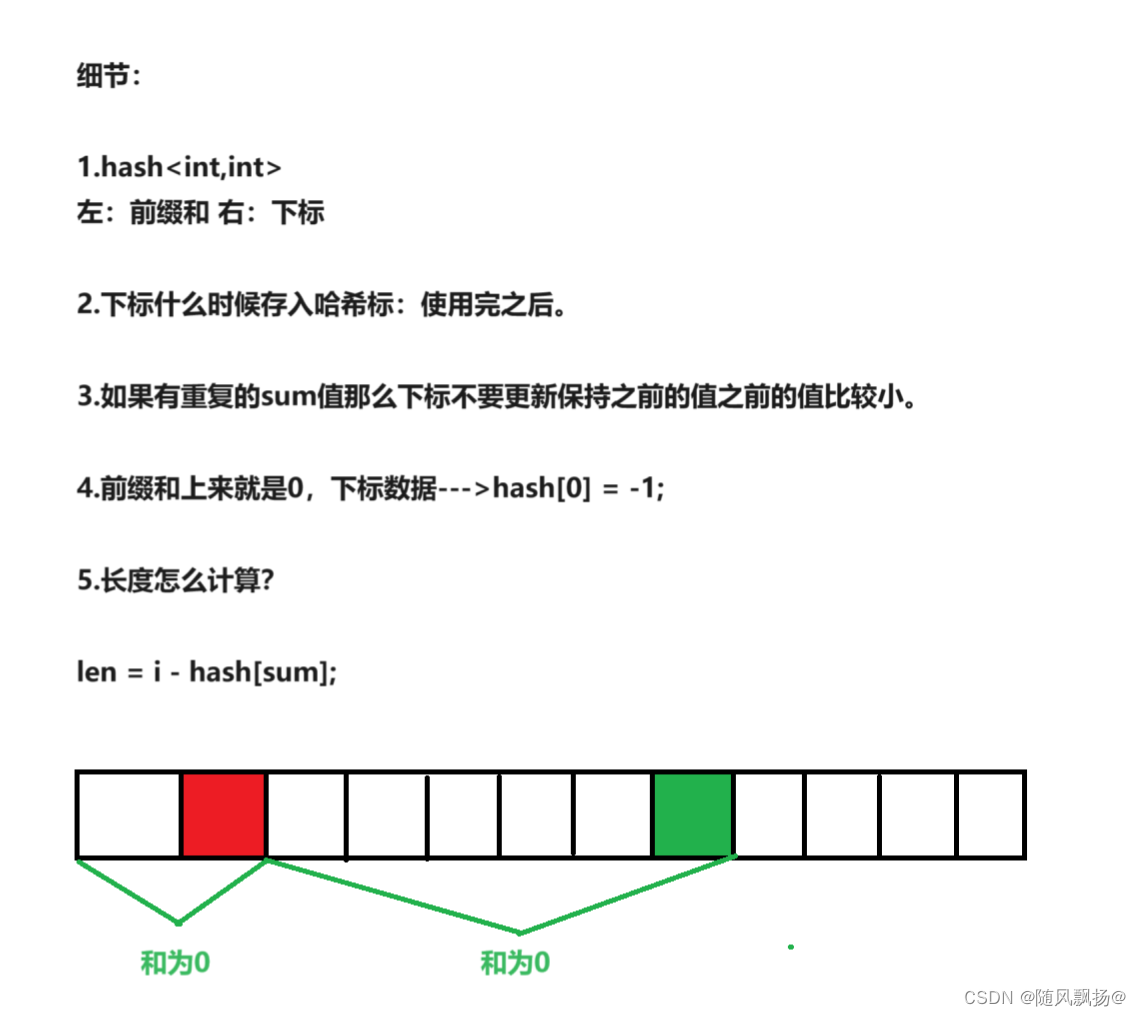
class Solution {
public:int findMaxLength(vector<int>& nums) {vector<int> nums_1(nums);for(auto& n:nums_1){if(n==0) n = -1;}//2.hash+前缀和的思路unordered_map<int,int> hash;//1.前缀和为0的下标处理:hash[0] = -1;int sum = 0,ret = 0;for(int i=0;i<nums.size();i++){sum+=nums_1[i];if(hash.count(sum)) ret = max(ret , i - hash[sum]);else hash[sum] = i;}return ret;}
};
八.矩阵区域和:

矩阵区域和
1.思路一:二维前缀和模板+细节处理
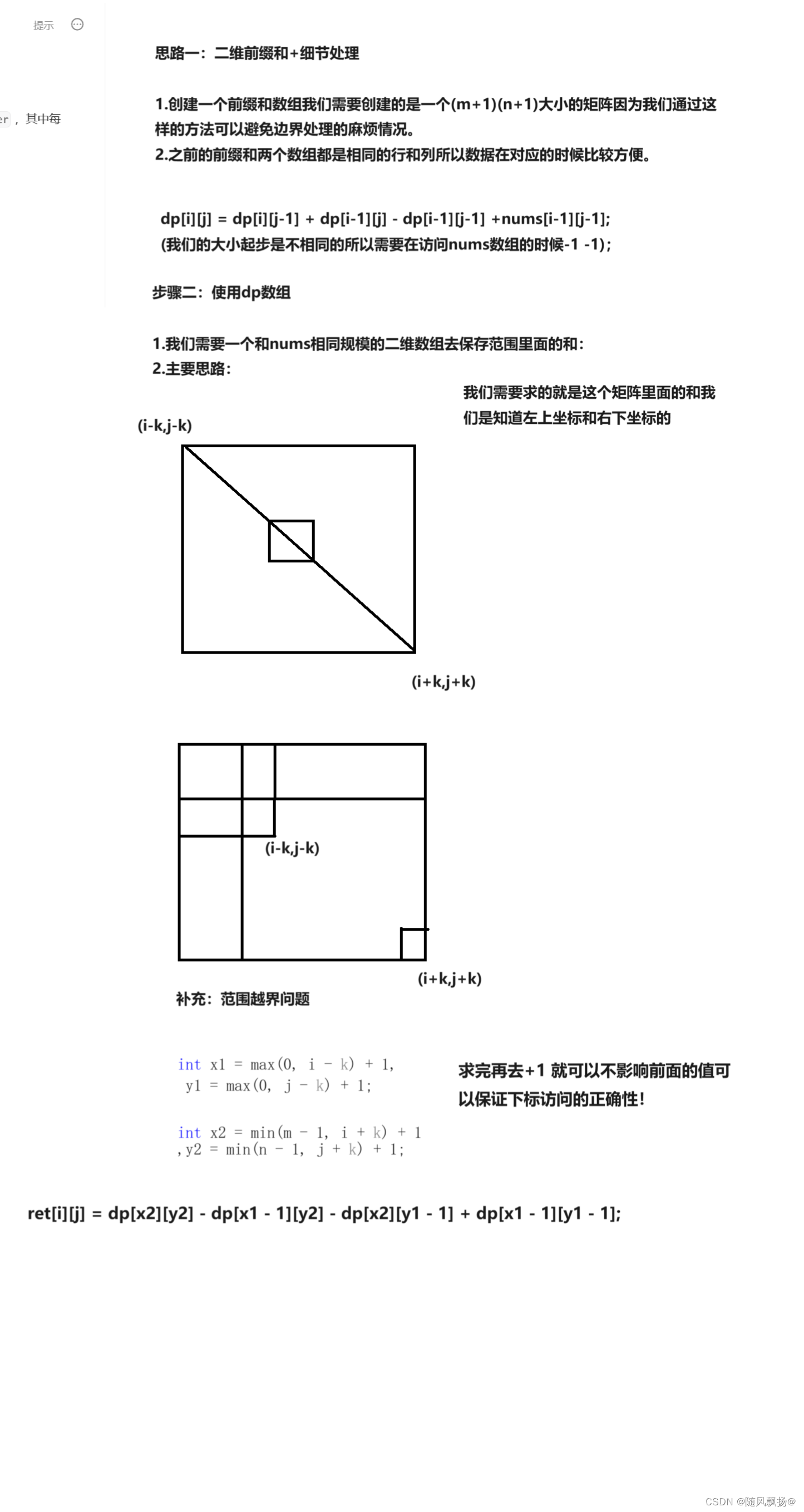
class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int m = mat.size();int n = mat[0].size();//1.创建(m+1) * (n+1) 大小的二维数组vector<vector<int>> dp(m+1 , vector<int>(n+1));//2.dp数组赋值:for(int i=1 ; i<=m ; i++){for(int j=1 ; j<=n ; j++){dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + mat[i-1][j-1];}}//3.使用dp数组并且考虑i-k 和 j-k的越界问题:vector<vector<int>> ret(m,vector<int>(n));for(int i=0 ; i<m ; i++){for(int j=0 ; j<n ; j++){int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1;int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1;ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] +dp[x1 - 1][y1 - 1];}}return ret;}
};
相关文章:

算法专题四:前缀和
前缀和 一.一维前缀和(模板):1.思路一:暴力解法2.思路二:前缀和思路 二. 二维前缀和(模板):1.思路一:构造前缀和数组 三.寻找数组的中心下标:1.思路一:前缀和 四.除自身以外数组的乘积ÿ…...
探索动画之帧动画)
STM32学习笔记十五:WS2812制作像素游戏屏-飞行射击游戏(5)探索动画之帧动画
本章又是个重要的章节——动画。 动画,本质上时一系列静态的画面连续播放,欺骗人眼产生动画效果。这个原理自打十九世纪电影诞生开始,就从来没变过。 我们的游戏中也需要一些动画效果,比如,被击中时的受伤效果&#…...
)
期末复习(程序设计)
根据字符出现频率排序 【问题描述】 给定一个字符串 s ,根据字符出现的 频率 对其进行降序排序。一个字符出现的频率是它出现在字符串中的次数。 返回已排序的字符串。 频率相同的的字符按ascii值降序排序。 s不包含空格、制表符、换行符等特殊字符。 【输入格…...
html-css-js移动端导航栏底部固定+i18n国际化全局
需求:要做一个移动端的仿照小程序的导航栏页面操作,但是这边加上了i18n国家化,由于页面切换的时候会导致国际化失效,所以写了这篇文章 1.效果 切换页面的时候中英文也会跟着改变,不会导致切换后回到默认的语言 2.实现…...

Ubuntu Linux 入门指南:面向初学者
目录 1. Ubuntu Linux 简介 Ubuntu 的由来 Ubuntu 与其他 Linux 发行版的比较 Debian: Fedora: openSUSE: Arch Linux: Linux Mint: 第二部分:安装 Ubuntu 1. 准备安装 系统需求 创建 Ubuntu 启…...

常见算法面试题目
前言 总结一些常见的算法题目,每一个题目写一行思路,方便大家复习。具体题目的来源是下面的网站。 剑指offer 剑指offe2 leetcode200题 leetcode 100题 leetcode150题 leetcode 75题 文章目录 前言二叉树非递归遍历牛客JZ31 栈的压入、弹出序列 (…...

PiflowX组件-JDBCWrite
JDBCWrite组件 组件说明 使用JDBC驱动向任意类型的关系型数据库写入数据。 计算引擎 flink 有界性 Sink: Batch Sink: Streaming Append & Upsert Mode 组件分组 Jdbc 端口 Inport:默认端口 outport:默认端口 组件属性 名称展示名称默…...

算法导论复习题目
这题需要考虑什么呢? 一换元,二要使用主方法猜出结果,三是证明的时候添加一个低阶项来消除 LC检索 C(x)是从上帝视角来看的成本 对C(x)的一个估计: 由两个部分组成,就相当于由以往的经验对未来…...
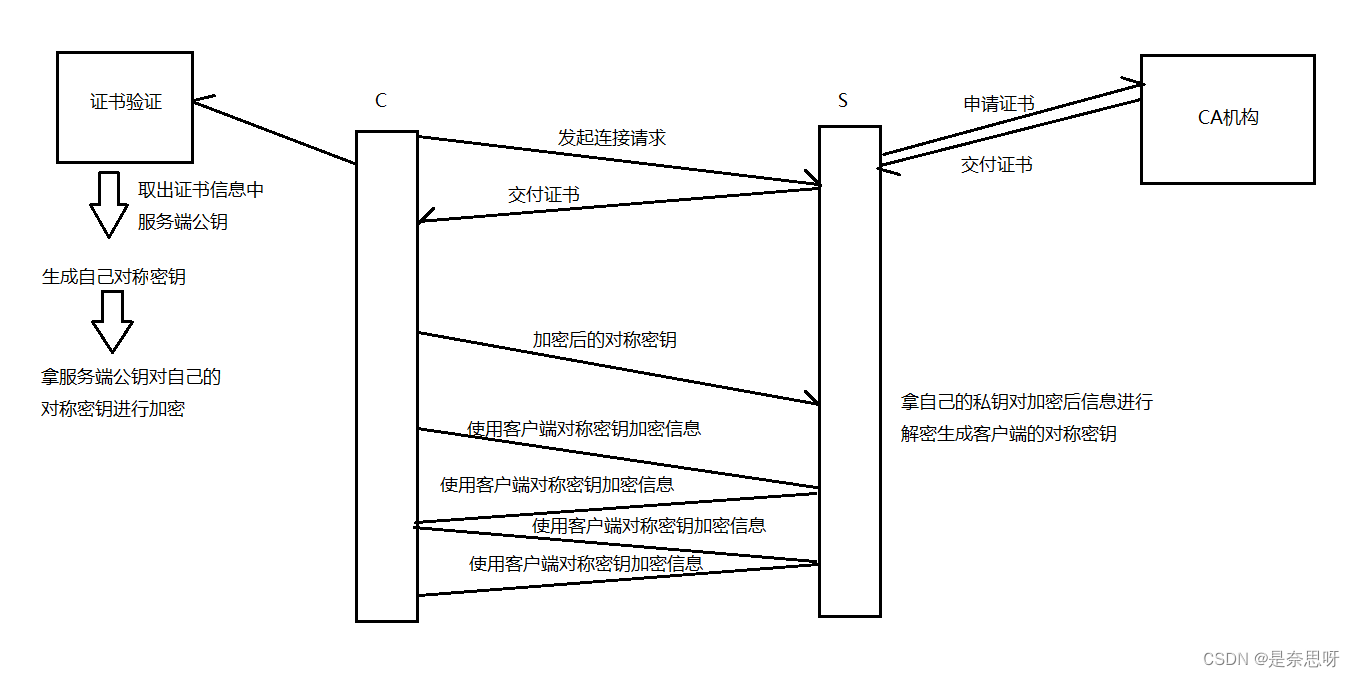
HTTPS协议详解
目录 前言 一、HTTPS协议 1、加密是什么 2、为什么要加密 二、常见加密方式 1、对称加密 2、非对称加密 三、数据摘要与数据指纹 1、数据摘要 2、数据指纹 四、HTTPS加密策略探究 1、只使用对称加密 2、只使用非对称加密 3、双方都使用非对称加密 4、对称加密非…...

菜鸟学习vue3笔记-vue3 router回顾
1、路由router pnpm i vue-router2、创建使用环境 1.src下创建 router文件夹、里面创建index.ts文件 //创建一个路由暴露出去//1.引入createRouter import { createRouter, createWebHistory } from "vue-router";// import Home from ../components/Home.vue//…...

Mybatis枚举类型处理和类型处理器
专栏精选 引入Mybatis Mybatis的快速入门 Mybatis的增删改查扩展功能说明 mapper映射的参数和结果 Mybatis复杂类型的结果映射 Mybatis基于注解的结果映射 Mybatis枚举类型处理和类型处理器 再谈动态SQL Mybatis配置入门 Mybatis行为配置之Ⅰ—缓存 Mybatis行为配置…...
2023 NCTF writeup
CRYPTO Sign 直接给了fx,gx,等于私钥给了,直接套代码,具体可以参考: https://0xffff.one/d/1424 fx [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…...

golang的大杀器协程goroutine
在Golang中,协程(Goroutine)是轻量级的执行单元,用于实现并发编程。它是Golang语言的重要组成部分,提供了简洁、高效的方式来处理并发任务。 特点: 1)轻量级:Go语言的协程是轻量级…...

[Angular] 笔记 9:list/detail 页面以及@Output
1. Output input 好比重力,向下传递数据,list 传给 detail,smart 组件传给 dumb 组件,父组件传给子组件。input 顾名思义,输入数据给组件。 output 与之相反,好比火箭,向上传递数据或事件。ou…...
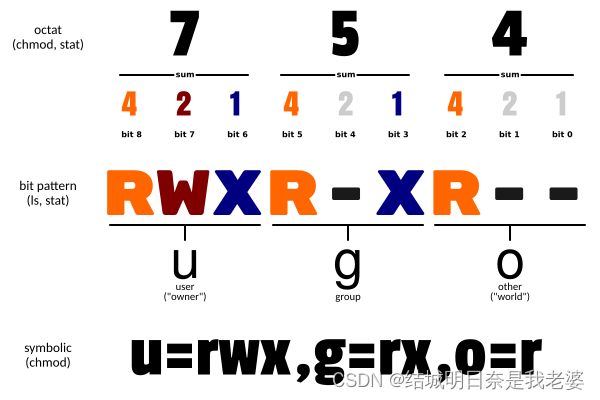
Linux学习笔记(一)
如果有自己的物理服务器请先查看这篇文章 文章目录 网卡配置Linux基础指令ls:列出目录内容cd(mkdir.rmkdir): 切换文件夹(创建,删除操作)cp:复制文件或目录mv:文件/文件夹移动cat:查看文件vi:文件查看编辑man:查看命令手册more: 查看文件内容less : 查看文件内容 ps: 显示当前进…...

Python 爬虫 教程
python爬虫框架:Scrapyd,Feapder,Gerapy 参考文章: python爬虫工程师,如何从零开始部署ScrapydFeapderGerapy? - 知乎 神器!五分钟完成大型爬虫项目 - 知乎 爬虫框架-feapder - 知乎 scrap…...
uniapp原生插件 - android原生插件打包流程 ( 避坑指南一)
【彩带- 避坑知识点】: 当时开发中安卓插件打包成功后,uniapp引用插件aar,用云打包 ,总是提示不包含插件。原因是因为module的androidManifest.xml文件没有注册activity。 这一步 很重要,一定要注册。 --------------------------…...
搭建maven私服
maven maven简介 什么是maven? Maven这个单词来自于意第绪语(犹太语),意为知识的积累。 Maven项目对象模型(POM),可以通过一小段描述信息来管理项目的构建,报告和文档的项目管理工具软件。 Maven 除了以…...
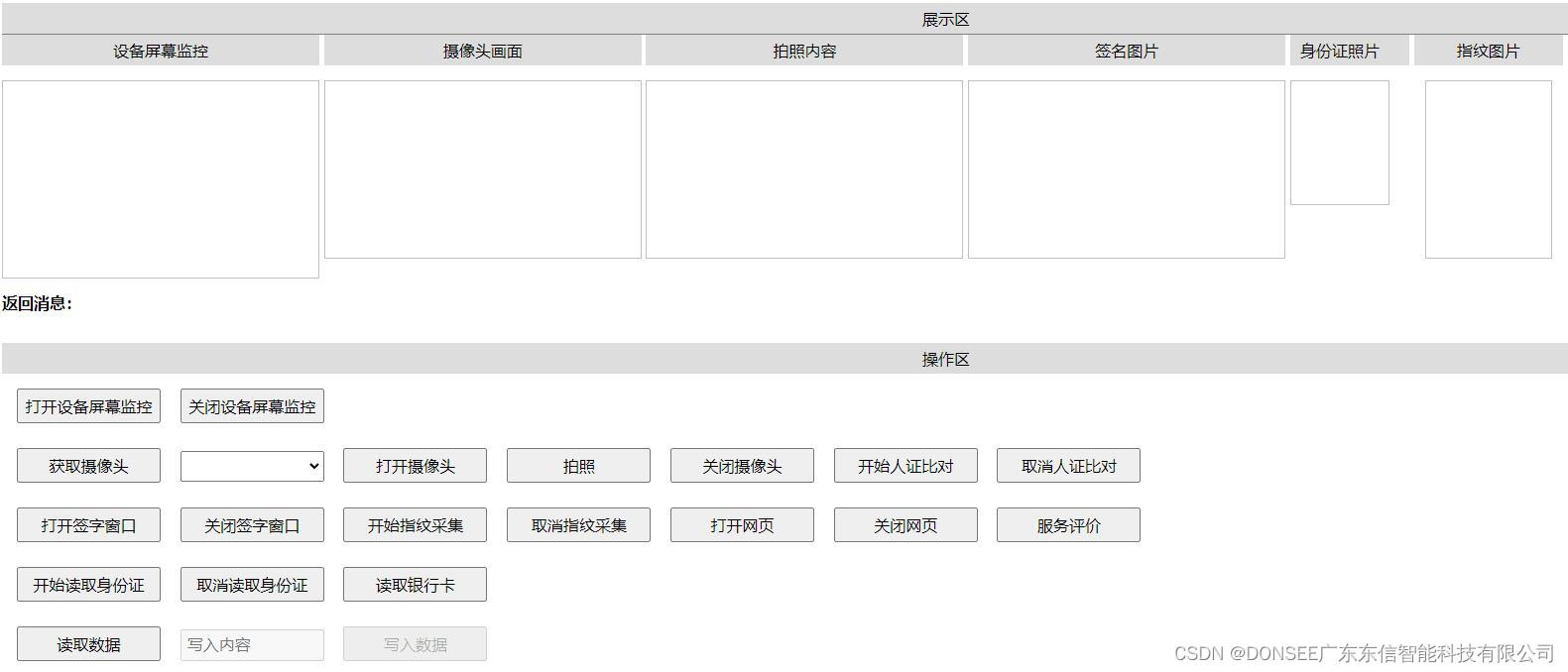
EST-100身份证社保卡签批屏按捺终端PC版web版本http协议接口文档,支持web网页开发对接使用
<!DOCTYPE html><html lang"zh-CN"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width,initial-scale1.0"><title>演示DEMO</title><script type"text/…...

基于SpringBoot的毕业论文管理系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于SpringBoot的毕业论文管理系统,java…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

