数据结构OJ实验9-图存储结构和遍历
A. 图综合练习--构建邻接表
题目描述
已知一有向图,构建该图对应的邻接表。
邻接表包含数组和单链表两种数据结构,其中每个数组元素也是单链表的头结点,数组元素包含两个属性,属性一是顶点编号info,属性二是指针域next指向与它相连的顶点信息。
单链表的每个结点也包含两个属性,属性一是顶点在数组的位置下标,属性二是指针域next指向下一个结点。
输入
第1行输入整数t,表示有t个图
第2行输入n和k,表示该图有n个顶点和k条弧。
第3行输入n个顶点。
第4行起输入k条弧的起点和终点,连续输入k行
以此类推输入下一个图
输出
输出每个图的邻接表,每行输出格式:数组下标 顶点编号-连接顶点下标-......-^,数组下标从0开始。
具体格式请参考样例数据,每行最后加入“^”表示NULL。
样例查看模式
正常显示查看格式
输入样例1
1\n
5 7\n
A B C D E\n
A B\n
A D\n
A E\n
B D\n
C B\n
C E\n
E D\n
输出样例1
0 A-1-3-4-^\n
1 B-3-^\n
2 C-1-4-^\n
3 D-^\n
4 E-3-^\n
AC代码
#include<iostream>
#include<vector>
#include<map>
using namespace std;
class graph
{int n, k;vector<int>h;vector<int>ne;vector<int>e;int idx;map<char, int>id;vector<char>value;
public:graph(){idx = 0;cin >> n >> k;h.resize(2 * n, -1);ne.resize(2 * n);e.resize(2 * n);for (int i = 0; i < n; i++){char c;cin >> c;id[c] = i;value.push_back(c);}for (int i = 0; i < k; i++){char u, v;cin >> u >> v;add(id[u], id[v]);}}void add(int a, int b){e[idx] = b;ne[idx] = h[a];h[a] = idx++;}void show(){for (int i = 0; i < n; i++){cout << i << " " << value[i] << "-";vector<int>ans;for (int j = h[i]; ~j; j = ne[j]){int k = e[j];ans.push_back(id[value[k]]);}//由于本题使用头插法,而此方法是尾插法,故要逆转for (int i=ans.size()-1;i>=0;i--){cout << ans[i] << "-";}cout << "^" << endl;}}
};
int main()
{int t;cin >> t;while (t--){graph g;g.show();}return 0;
}B. DS图—图的邻接矩阵存储及度计算
题目描述
假设图用邻接矩阵存储。输入图的顶点信息和边信息,完成邻接矩阵的设置,并计算各顶点的入度、出度和度,并输出图中的孤立点(度为0的顶点)
--程序要求--
若使用C++只能include一个头文件iostream;若使用C语言只能include一个头文件stdio
程序中若include多过一个头文件,不看代码,作0分处理
不允许使用第三方对象或函数实现本题的要求
输入
测试次数T,每组测试数据格式如下:
图类型 顶点数 (D—有向图,U—无向图)
顶点信息
边数
每行一条边(顶点1 顶点2)或弧(弧尾 弧头)信息
输出
每组测试数据输出如下信息(具体输出格式见样例):
图的邻接矩阵
按顶点信息输出各顶点的度(无向图)或各顶点的出度 入度 度(有向图)。孤立点的度信息不输出。
图的孤立点。若没有孤立点,不输出任何信息。
样例查看模式
正常显示查看格式
输入样例1
2\n
D 5\n
V1 V2 V3 V4 V5\n
7\n
V1 V2\n
V1 V4\n
V2 V3\n
V3 V1\n
V3 V5\n
V4 V3\n
V4 V5\n
U 5\n
A B C D E\n
5\n
A B\n
A C\n
B D\n
D C\n
A D
输出样例1
0 1 0 1 0\n
0 0 1 0 0\n
1 0 0 0 1\n
0 0 1 0 1\n
0 0 0 0 0\n
V1: 2 1 3\n
V2: 1 1 2\n
V3: 2 2 4\n
V4: 2 1 3\n
V5: 0 2 2\n
0 1 1 1 0\n
1 0 0 1 0\n
1 0 0 1 0\n
1 1 1 0 0\n
0 0 0 0 0\n
A: 3\n
B: 2\n
C: 2\n
D: 3\n
E
AC代码
#include<iostream>
using namespace std;
//输入测试次数,每组测试:
//图类型,顶点数
//顶点信息,边数,每条边的头尾
//输出每个点的出度和入度,单独输出孤立点
class Map
{int vertexnum;string* vertex;int** adjmatrix;char kind;
public:Map(){cin >> kind >> vertexnum;vertex = new string[vertexnum];for (int i = 0; i < vertexnum; i++){cin >> vertex[i];}adjmatrix = new int* [vertexnum];for (int i = 0; i < vertexnum; i++){adjmatrix[i] = new int[vertexnum];for (int j = 0; j < vertexnum; j++){adjmatrix[i][j] = 0;}}int n;cin >> n;for (int i = 0; i < n; i++){string s1, s2;cin >> s1 >> s2;int index1 = 0;int index2 = 0;for (int j = 0; j < vertexnum; j++){if (vertex[j] == s1){index1 = j;break;}}for (int j = 0; j < vertexnum; j++){if (vertex[j] == s2){index2 = j;break;}}switch (kind){case 'U':adjmatrix[index2][index1] = 1;case 'D':adjmatrix[index1][index2] = 1;default:break;}}}void display_array(){for (int i = 0; i < vertexnum; i++){cout << adjmatrix[i][0];for (int j = 1; j < vertexnum; j++){cout << " " << adjmatrix[i][j];}cout << endl;}}void display_node(){if (kind == 'U'){for (int i = 0; i < vertexnum; i++){int cnt = 0;for (int j = 0; j < vertexnum; j++){if (adjmatrix[i][j] != 0){cnt++;}}if (cnt){cout << vertex[i] << ": " << cnt << endl;}else{cout << vertex[i] << endl;}}}else if (kind == 'D'){for (int i = 0; i < vertexnum; i++){int cnt1 = 0;for (int j = 0; j < vertexnum; j++){if (adjmatrix[i][j] != 0){cnt1++;}}int cnt2 = 0;for (int j = 0; j < vertexnum; j++){if (adjmatrix[j][i] != 0){cnt2++;}}if (cnt1 || cnt2)//存在其中一个就不是孤立点{cout << vertex[i] << ": " << cnt1 << " " << cnt2 << " " << cnt1 + cnt2 << endl;}else{cout << vertex[i] << endl;}}}}~Map(){delete[]vertex;for (int i = 0; i < vertexnum; i++){delete[]adjmatrix[i];}delete[]adjmatrix;}
};
int main()
{int n;cin >> n;while (n--){Map m;m.display_array();m.display_node();}return 0;
}C. DS图遍历--深度优先搜索
题目描述
给出一个图的邻接矩阵,对图进行深度优先搜索,从顶点0开始
代码框架参考课本P169算法7.4和7.5,同学们可在理解的基础上自行设计算法,不强制要求完全相同
注意:图n个顶点编号从0到n-1
输入
第一行输入t,表示有t个测试实例
第二行输入n,表示第1个图有n个结点
第三行起,每行输入邻接矩阵的一行,以此类推输入n行
第i个结点与其他结点如果相连则为1,无连接则为0,数据之间用空格隔开
以此类推输入下一个示例
输出
每行输出一个图的深度优先搜索结果,结点编号之间用空格隔开
样例查看模式
正常显示查看格式
输入样例1
2\n
4\n
0 0 1 1\n
0 0 1 1\n
1 1 0 1\n
1 1 1 0\n
5\n
0 0 0 1 1\n
0 0 1 0 0\n
0 1 0 1 1\n
1 0 1 0 0\n
1 0 1 0 0\n
输出样例1
0 2 1 3 \n
0 3 2 1 4 \n
AC代码
#include<bits/stdc++.h>
using namespace std;
int main()
{int t;cin >> t;while (t--){int n;cin >> n;vector<vector<int>>v(n);for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){int x;cin >> x;v[i].push_back(x);}}vector<int>st(n);//标记是否已经走过stack<int>s;//深度优先搜索使用栈for (int i = 0; i < n; i++)//每个结点都要搜一次,确定每个都走过{if (st[i])continue;s.push(i);while (!s.empty())//每个点开始搜{auto t = s.top();s.pop();if (st[t])continue;st[t] = 1;cout << t << " ";//满足条件可以搜//注意逆序枚举连接点//因为是栈,先进去后出来for (int j = n - 1; j >= 0; j--){if (v[t][j] && !st[j]){s.push(j);}}}}cout << endl;}return 0;
}D. DS图遍历--广度优先搜索
题目描述
给出一个图的邻接矩阵,对图进行广度优先搜索,从顶点0开始
注意:图n个顶点编号从0到n-1
输入
第一行输入t,表示有t个测试实例
第二行输入n,表示第1个图有n个结点
第三行起,每行输入邻接矩阵的一行,以此类推输入n行
第i个结点与其他结点如果相连则为1,无连接则为0,数据之间用空格隔开
以此类推输入下一个示例
输出
每行输出一个图的广度优先搜索结果,结点编号之间用空格隔开
样例查看模式
正常显示查看格式
输入样例1
2\n
4\n
0 0 1 1\n
0 0 1 1\n
1 1 0 1\n
1 1 1 0\n
5\n
0 0 0 1 1\n
0 0 1 0 0\n
0 1 0 1 1\n
1 0 1 0 0\n
1 0 1 0 0\n
输出样例1
0 2 3 1 \n
0 3 4 2 1 \n
AC代码
#include<bits/stdc++.h>
using namespace std;
int main()
{int t;cin >> t;while (t--){int n;cin >> n;vector<vector<int>>v(n);for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){int x;cin >> x;v[i].push_back(x);}}vector<int>st(n);//标记是否已经走过queue<int>s;//广度搜索使用队列for (int i = 0; i < n; i++)//每个结点都要搜一次,确定每个都走过{if (st[i])continue;s.push(i);while (!s.empty())//每个点开始搜{auto t = s.front();s.pop();if (st[t])continue;st[t] = 1;cout << t << " ";//满足条件可以搜//注意顺序枚举连接点//因为是队列,先进去先出来for (int j = 0; j<=n-1;j++){if (v[t][j] && !st[j]){s.push(j);}}}}cout << endl;}return 0;
}E. DS图—图非0面积
题目描述
编程计算由"1"围成的下列图形的面积。面积计算方法是统计"1"所围成的闭合曲线中"0"点的数目。如图所示,在10*10的二维数组中,"1"围住了15个点,因此面积为15。

提示:queue
输入
测试次数t
每组测试数据格式为:
数组大小m,n
一个由0和1组成的m*n的二维数组
输出
对每个二维数组,输出符号"1"围住的"0"的个数,即围成的面积。假设一定有1组成的闭合曲线,但不唯一。
样例查看模式
正常显示查看格式
输入样例1
2\n
10 10\n
0 0 0 0 0 0 0 0 0 0\n
0 0 0 0 1 1 1 0 0 0\n
0 0 0 0 1 0 0 1 0 0\n
0 0 0 0 0 1 0 0 1 0\n
0 0 1 0 0 0 1 0 1 0\n
0 1 0 1 0 1 0 0 1 0\n
0 1 0 0 1 1 0 1 1 0\n
0 0 1 0 0 0 0 1 0 0\n
0 0 0 1 1 1 1 1 0 0\n
0 0 0 0 0 0 0 0 0 0\n
5 8\n
0 1 1 0 0 1 1 0\n
1 0 1 0 1 0 0 1\n
0 1 0 1 0 0 1 0\n
0 1 0 0 1 1 1 0\n
0 0 0 0 0 0 0 0\n
输出样例1
15\n
5\n
#include<bits/stdc++.h>
using namespace std;
int n,m;
int dx[]={1,-1,0,0};
int dy[]={0,0,-1,1};
vector<vector<int>>v;
void dfsfind(int x,int y)
{if(x<0||y<0||x>=m||y>=n||v[x][y])return;v[x][y]=1;for(int i=0;i<4;i++){dfsfind(x+dx[i],y+dy[i]);}
}
int main()
{int t;cin>>t;while(t--){v.clear();cin>>m>>n;v.resize(m);for(int i=0;i<m;i++){for(int j=0;j<n;j++){int x;cin>>x;v[i].push_back(x);}}int ans=0;for(int i=0;i<m;i++)//先按行{dfsfind(i,0);dfsfind(i,n-1);}for(int i=0;i<n;i++)//后按列{dfsfind(0,i);dfsfind(m-1,i);}for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(v[i][j]==0)ans++;}}cout<<ans<<endl;}return 0;
}F. 社交网络图中结点的“重要性”计算
题目描述
在社交网络中,个人或单位(结点)之间通过某些关系(边)联系起来。他们受到这些关系的影响,这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用,可以增强也可以减弱。而结点根据其所处的位置不同,其在网络中体现的重要性也不尽相同。
“紧密度中心性”是用来衡量一个结点到达其它结点的“快慢”的指标,即一个有较高中心性的结点比有较低中心性的结点能够更快地(平均意义下)到达网络中的其它结点,因而在该网络的传播过程中有更重要的价值。在有N个结点的网络中,结点vi的“紧密度中心性”Cc(vi)数学上定义为vi到其余所有结点vj (j=i) 的最短距离d(vi,vj)的平均值的倒数:
对于非连通图,所有结点的紧密度中心性都是0。
给定一个无权的无向图以及其中的一组结点,计算这组结点中每个结点的紧密度中心性。
输入
输入第一行给出两个正整数N和M,其中N(≤104)是图中结点个数,顺便假设结点从1到N编号;M(≤105)是边的条数。随后的M行中,每行给出一条边的信息,即该边连接的两个结点编号,中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K(≤100)以及K个结点编号,用空格分隔。
输出
按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性,每个输出占一行,结果保留到小数点后2位。
样例查看模式
正常显示查看格式
输入样例1
9 14\n
1 2\n
1 3\n
1 4\n
2 3\n
3 4\n
4 5\n
4 6\n
5 6\n
5 7\n
5 8\n
6 7\n
6 8\n
7 8\n
7 9\n
3 3 4 9
输出样例1
Cc(3)=0.47\n
Cc(4)=0.62\n
Cc(9)=0.35
AC代码
#include<bits/stdc++.h>
using namespace std;
//求一个点到其余各点的最短路->FLoyd
const int N = 1000, inf = 1e9;
long long res = 0;
int n, m, k;
int d[N][N];
void floyd()
{for (int k = 1; k <= n; k++)//中间点枚举放在首个循环{for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){d[i][j] = min(d[i][j], d[i][k] + d[k][j]);}}}
}
int main()
{cin >> n >> m;//注意弗洛伊德的初始for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){if (i == j)d[i][j] = 0;else d[i][j] = inf;}}for (int i = 0; i < m; i++){int a, b;cin >> a >> b;d[a][b] = d[b][a] = 1;//无向图}floyd();bool flag = 0;cin >> k;for (int i = 0; i < k; i++) {res = 0;int x;cin >> x;if (!flag){for (int j = 1; j <= n; j++){if (x == j)continue;if (d[x][j] > inf / 2)//此时不连通{flag = 1;break;}res += d[x][j];}}if (flag)printf("Cc(%d)=0.00\n", x);//无法满足到其余所有点else{double ans = (double)(n - 1) / res;printf("Cc(%d)=%.2lf\n", x, ans);}}return 0;
}相关文章:

数据结构OJ实验9-图存储结构和遍历
A. 图综合练习--构建邻接表 题目描述 已知一有向图,构建该图对应的邻接表。 邻接表包含数组和单链表两种数据结构,其中每个数组元素也是单链表的头结点,数组元素包含两个属性,属性一是顶点编号info,属性二是指针域n…...

20231226在Firefly的AIO-3399J开发板上在Android11下调通后摄像头ov13850
20231226在Firefly的AIO-3399J开发板上在Android11下调通后摄像头ov13850 2023/12/26 8:22 开发板:Firefly的AIO-3399J【RK3399】 SDK:rk3399-android-11-r20211216.tar.xz【Android11】 Android11.0.tar.bz2.aa【ToyBrick】 Android11.0.tar.bz2.ab And…...

0101包冲突导致安装docker失败-docker-云原生
文章目录 1 前言2 报错3 解决结语 1 前言 最近在学习k8s,前置条件就是要安装指定版本的docker,命令如下 yum install -y docker-ce-20.10.7 docker-ce-cli-20.10.7 containerd.io-1.4.62 报错 file /usr/libexec/docker/cli-plugins/docker-buildx fr…...

【力扣100】17.电话号码的字母组合
添加链接描述 class Solution:def letterCombinations(self, digits: str) -> List[str]:# 思路是使用回溯算法if not digits:return []phone {2:[a,b,c],3:[d,e,f],4:[g,h,i],5:[j,k,l],6:[m,n,o],7:[p,q,r,s],8:[t,u,v],9:[w,x,y,z]}def backtrack(con,dig):# 收获if le…...

2023。
一月 从头开始 二月 准备复试&初试成绩 三月 最开心 过了两个生日(这机率,幸运儿) 考研也成功上岸!nnuGISer! 四月 和室友去了趟武汉 五月 拍毕业照 六月 人生高光时刻 省创!上台领奖!考研…...

出现 Cause: java.sql.SQLException: Field ‘id‘ doesn‘t have a default value解决方法
目录 1. 问题所示2. 原理分析3. 解决方法1. 问题所示 在驱动Springboot项目的时候,出现如下问题: org.springframework.dao.DataIntegrityViolationException: ### Error updating database. Cause: java.sql...

Linux--批量自动装机
实验环境 随着某公司业务不断发展,服务器主机的数量也迅速增长,对于功能变更或新采购的服务器, 需要重新安装CentOS7操作系统,为了提高服务器装机效率,要求基于PXE网络实现全自动无人值 守批量安装。 需求描述 > 服…...
病理HE学习贴(自备)
目录 正常结构 癌症HE 在线学习 以胃癌的学习为例 正常结构 1:胃粘膜正常结构和细胞分化 ●表面覆盖小凹上皮细胞(主要标志物:MUC5AC)以保护黏膜。 ●胃底腺固有腺体由黏液颈细胞(MUC6)、主细胞(Pepsinogen l)和壁细胞(Proton pump α-subunit)组…...

关于协同过滤算法在物联网的应用-基于用户行为数据和物联网设备数据,以此提供个性化的智能家居控制推荐服务
关于协同过滤算法在物联网领域的应用的一个案例是基于用户行为数据和物联网设备数据,为用户提供个性化的智能家居控制推荐服务。 具体实现如下: 数据收集:收集用户对智能家居设备的使用行为数据,包括设备的打开、关闭、调节等操…...
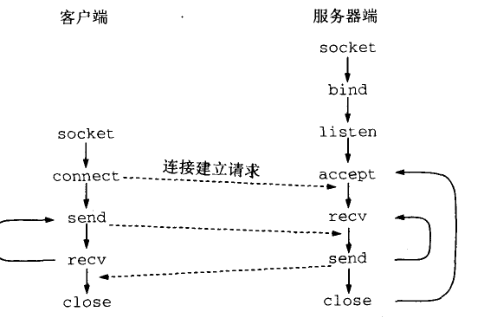
计算机网络(6):应用层
每个应用层协议都是为了解决某一类应用问题,而问题的解决又往往是通过位于不同主机中的多个应用进程之间的通信和协同工作来完成的。 应用层的具体内容就是规定应用进程在通信时所遵循的协议。 应用层的许多协议都是基于客户服务器方式。即使是对等通信方式&#x…...
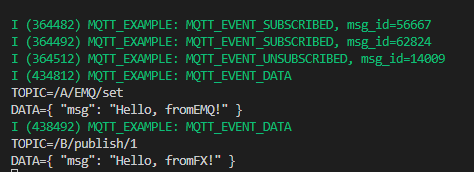
ESP32:整合存储配网信息和MQTT笔记
文章目录 1.给LED和KEY的所用IO增加配置项1.1 增加配置文件1.2 修改相应的c源码 2. 把mqtt\tcp的工程整合到一起2.1 在何处调用 mqtt_app_start() 3. 测试MQTT4. 完整的工程源码 有一段时间没有玩ESP32,很多知识点都忘记了。今天测试一下MQTT,做个笔记。…...
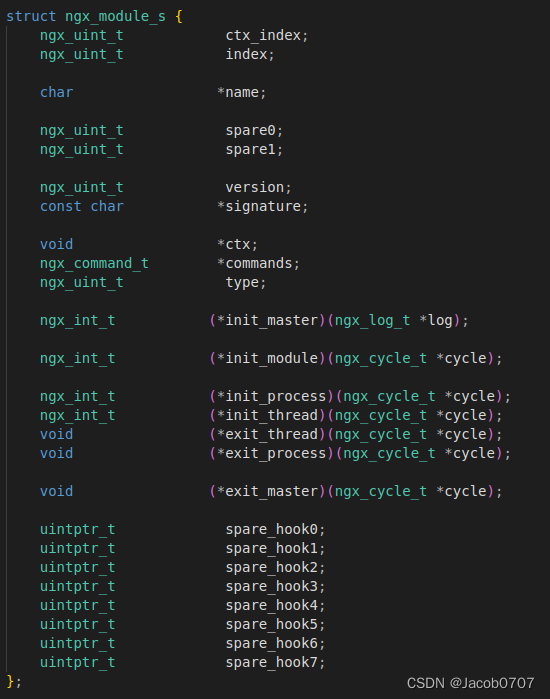
nginx源码分析-4
这一章内容讲述nginx的模块化。 ngx_module_t:一个结构体,用于描述nginx中的各个模块,其中包括核心模块、HTTP模块、事件模块等。这个结构体包含了一些模块的关键信息和回调函数,以便nginx在运行时能够正确地加载和管理这些模块。…...

【Unity美术】Unity工程师对3D模型需要达到的了解【二】
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...

《微信小程序开发从入门到实战》学习六十九
6.6 网络API 6.6.3 下载文件API 使用 wx.downloadFile 接口是可使小程序发起HTTPS GET请求,下载文件到手机端。 单次下载的最大文件为50MB。接受Obkect参,参支持属性如下: url(必填):下载文件的URL he…...
2022年全球软件质量效能大会(QECon北京站2022)-核心PPT资料下载
一、峰会简介 当前,新一轮科技革命和产业变革正在重塑全球经济格局,以云计算为代表的新一代信息技术创新活跃,与实体经济深度融合,推动泛在连接、数据驱动、智能引领的数字经济新形式孕育而生。 新兴技术的出现给测试乃至整个软…...

ILI9481 TFT3.5寸屏STM32F446ZEXX FMC驱动方式详解
图片来源于网络,如若侵权请联系博主删除 文章目录 1. 背景2. 基础知识2.1 TFT-LCD2.2 硬件接线2.3 FMC2.4 ILI9481 3. 软件抽象 1. 背景 最近做项目需要,博主在某宝上买了一块3.5寸的TFT屏,店家虽然发了资料,但是往产品上移植驱动…...
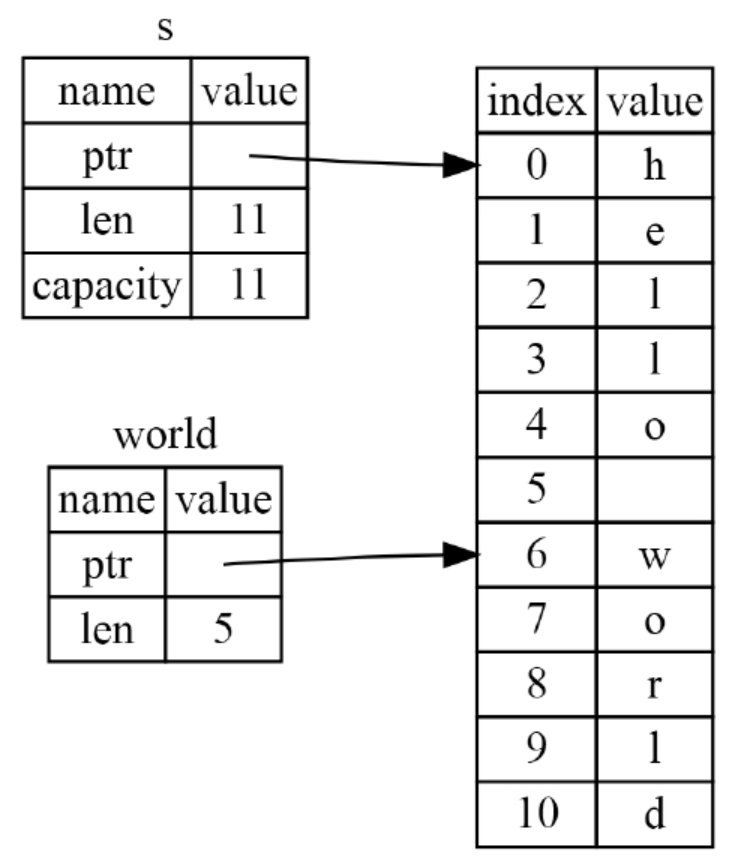
010、切片
除了引用,Rust还有另外一种不持有所有权的数据类型:切片(slice)。切片允许我们引用集合中某一段连续的元素序列,而不是整个集合。 考虑这样一个小问题:编写一个搜索函数,它接收字符串作为参数&a…...

【华为数据之道学习笔记】8-6 质量改进
数据质量改进致力于增强满足数据质量要求的能力。数据质量改进消除系统性的问题,对现有的质量水平在控制的基础上加以提高,使质量达到一个新水平、新高度。 质量改进的步骤本身就是一个PDCA循环。质量改进包括涉及企业跨组织的变革性改进(BTM…...
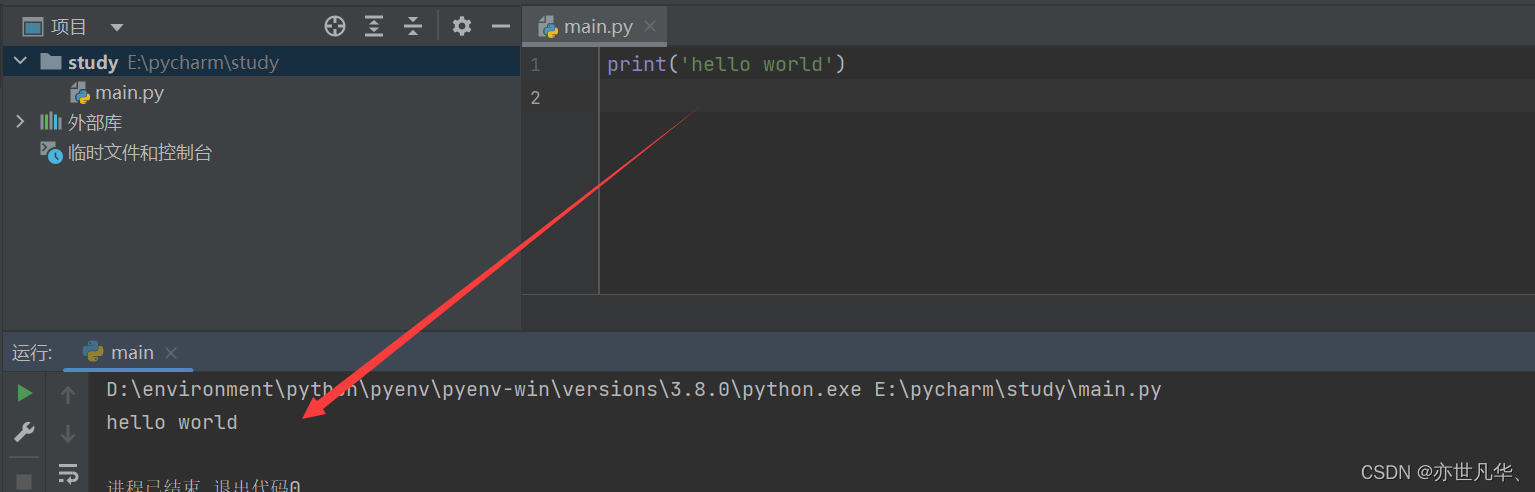
python多环境管理工具——pyenv-win安装与使用教程
目录 pyenv-win简介 pyenv-win安装 配置环境变量 pyenv的基本命令 pyenv安装py环境 pyenv安装遇到问题 pycharm测试 pyenv-win简介 什么是pyenv-win: 是一个在windows系统上管理python版本的工具。它是pyenv的windows版本,旨在提供类似于unix/li…...
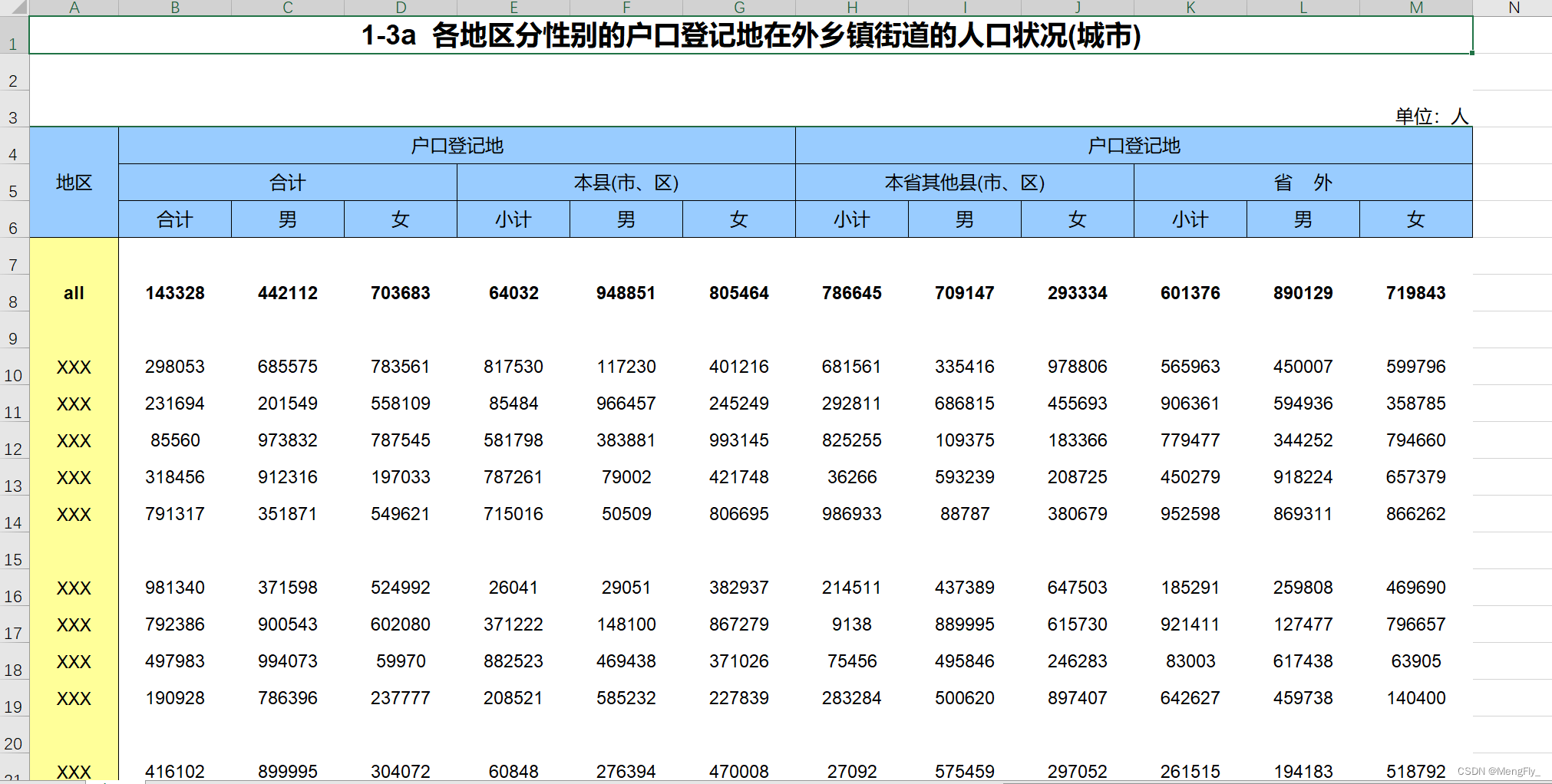
Excel报表框架(ExcelReport)极简化解决复杂报表导出问题
Excel Report 耗费了半个月的时间,终于在元旦这三天把报表框架开发完成了,使用该框架你可以非常方便的导出复杂的Excel报表。 项目开源地址: GiteeGithub 前言 不知道各位在使用POI开发报表导出过程中遇到过以下的情况: 频繁…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
