堆的应用:堆排序和TOP-K问题
上次才讲完堆的相关问题:二叉树顺序结构与堆的概念及性质(c语言实现堆
那今天就接着来进行堆的主要两方面的应用:堆排序和TOP-K问题
文章目录
- 1.堆排序
- 1.1概念、思路及代码
- 1.2改良代码(最初建立大堆用AdjustDow)
- 2. TOP-K问题
1.堆排序
1.1概念、思路及代码
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
- 建立堆
- 升序:建立大堆
- 降序:建立小堆
- 利用堆删除思想来进行排序:堆顶元素是当前堆中的最大值(大堆)或最小值(小堆),将堆顶元素与堆中最后一个元素交换,然后将剩余元素重新调整成堆,再取出堆顶元素。重复上述步骤,直到所有元素都被取出,即完成了排序
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}void AdjustUp(HPDataType* a, int child)
{int father = (child - 1) / 2;while (child > 0){if (a[child] > a[father]){Swap(&a[child], &a[father]);//更新下标child = father;father = (father - 1) / 2;}else{break;//一旦符合小堆了,就直接退出}}
}void AdjustDown(HPDataType* a, int n, int father)
{int child = father * 2 + 1;//假设左孩子大while (child < n){if (child + 1 < n && a[child] < a[child + 1]){child++;}if (a[child] > a[father]){Swap(&a[child], &a[father]);father = child;child = father * 2 + 1;}else{break;}}
}void HeapSort(int* arr, int n)//升序
{//先建大堆for (int i = 0; i < n; i++){AdjustUp(arr, i);}int a = n - 1;while (a > 0){//此时最大的是堆顶,堆顶跟最后一个交换Swap(&arr[0], &arr[a]);//现在最大的已经在最后了,不考虑它,把新塔顶降下来,重新编程大堆AdjustDown(arr, a, 0);a--;}}int main()
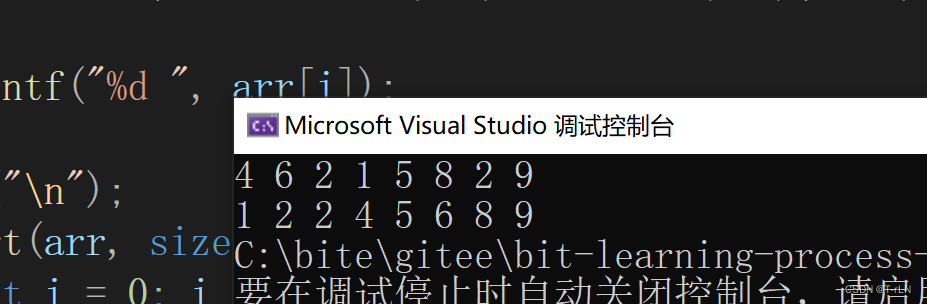
{int arr[]= { 4,6,2,1,5,8,2,9 };for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}printf("\n");HeapSort(arr, sizeof(arr) / sizeof(int));for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}
}
结果:
1.2改良代码(最初建立大堆用AdjustDow)
仅仅该那一部分:
void HeapSort(int* arr, int n)//升序
{//先建大堆//for (int i = 0; i < n; i++)//{// AdjustUp(arr, i);//}for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, n, i);}int a = n - 1;while (a > 0){//此时最大的是堆顶,堆顶跟最后一个交换Swap(&arr[0], &arr[a]);//现在最大的已经在最后了,不考虑它,把新塔顶降下来,重新编程大堆AdjustDown(arr, a, 0);a--;}}
对于一个具有n个节点的完全二叉树来说,最后一个非叶子节点的下标是(n-1-1)/2,也就是说,从最后一个非叶子节点开始,依次向上调整每个节点,就可以建立一个大堆
相比于向上调整,向下调整的好处:时间复杂度低
- 向下调整的时间复杂度是O(n),而向上调整的时间复杂度是O(nlogn)
建堆的时间复杂度为 O(n),排序过程的时间复杂度为 O(n log n)(建堆的时间复杂度为 O(n),而对堆进行排序的过程中,需要进行 n-1 次堆调整操作,每次堆调整的时间复杂度为 O(log n)。因此,排序过程的时间复杂度为 O(n log n))
2. TOP-K问题
TOP-K问题:求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大
对于Top-K问题,能想到的最简单直接的方式就是排序,然后直接取。 但是:如果数据量非常大,排序就不 太可取了,最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆
- 要找前k个最大的元素,则建小堆
- 要找前k个最小的元素,则建大堆
- 用剩余的元素依次与堆顶元素来比较,不满足则替换堆顶元素:
- 要找前k个最大的元素:但凡剩余的有比小堆堆顶大的就进入到堆里面,然后向下沉;如果建立大堆有可能一个都进不来。
- 找前k个最小的也同理
void CreateData()//用来创建有随机数的文件的进行检测
{int N = 1000;srand(time(0));FILE* f = fopen("data.txt", "w");for (int i = 0; i < N; i++){int a = (rand()) % 10000;fprintf(f,"%d\n", a);}fclose(f);}void PrintTopK(int k)//前k个大的
{//先读文件FILE* fout = fopen("data.txt", "r");if (fout == NULL){perror("fopen file");return -1;}int* a = (int*)malloc(sizeof(int) * k);for (int i = 0; i < k; i++)//建立元素k的小堆{fscanf(fout, "%d", &a[i]);//把文件里的前k个数字写入数组里AdjustUp(a, k);}//如果有比堆顶大的,就进来int n = 0;while (fscanf(fout, "%d", &n) != EOF)//读到文件读完就停止{if (n > a[0]){a[0] = n;AdjustDown(a, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", a[i]);}printf("\n");fclose(fout);
}int main()
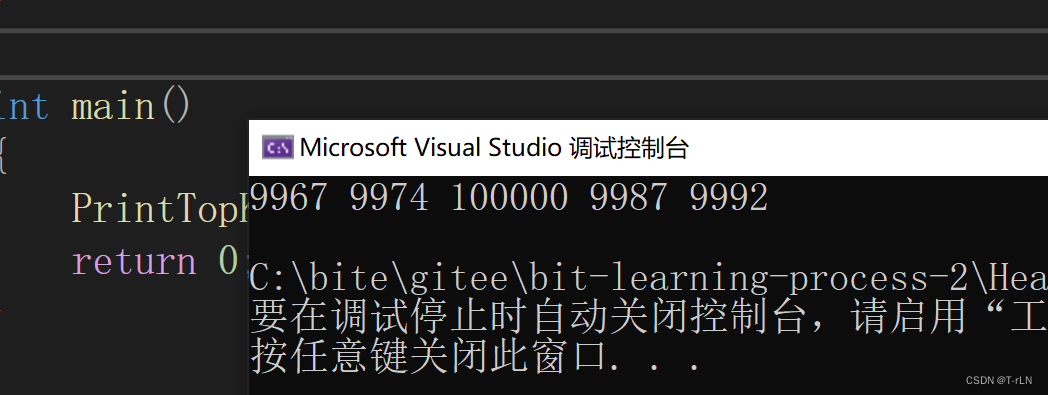
{PrintTopK(5);return 0;
}
结果如下:
那这次堆的两大应用就先到这里啦,到此二叉树顺序结构部分的知识也已经分享完毕了。感谢大家的支持,希望能帮助到大家!!!
相关文章:

堆的应用:堆排序和TOP-K问题
上次才讲完堆的相关问题:二叉树顺序结构与堆的概念及性质(c语言实现堆 那今天就接着来进行堆的主要两方面的应用:堆排序和TOP-K问题 文章目录 1.堆排序1.1概念、思路及代码1.2改良代码(最初建立大堆用AdjustDow) 2. TO…...
element表格排序功能
官方展示 个人项目 可以分别对每一项数据进行筛选 注:筛选的数据不能是字符串类型必须是数字类型,否则筛选会乱排序 html <el-table :data"tableData" border height"600" style"width: 100%"><el-table-co…...

HNU-Java程序设计基础训练-2023
1.DNA序列(Java) 【问题描述】 一个DNA序列由A/C/G/T四个字母的排列组合组成。G和C的比例(定义为GC-Ratio)是序列中G和C两个字母的总的出现次数除以总的字母数目(也就是序列长度)。在基因工程中…...

数据库和数据库编程
数据库、数据表、表数据操作以及数据库编程相关的知识点 1. 数据库的概念: 数据库是用于存储和组织数据的系统。数据库管理系统(DBMS)是管理数据库的软件,提供对数据的访问、查询和维护。关系型数据库是一种通过表格结构来组织和管理数据的数据库。 2…...
爬虫基础一(持续更新)
爬虫概念: 通过编写程序,模拟浏览器上网,然后让其去互联网上抓取数据的过程 分类: 1,通用爬虫:抓取一整张页面数据 2,聚焦爬虫:抓取页面中的局部内容 3,增量式爬虫&…...
右键菜单“以notepad++打开”,在windows文件管理器中
notepad 添加到文件管理器的右键菜单中 找到安装包,重新安装一般即可。 这里有最新版:地址 密码:f0f1 方法 在安装的时候勾选 “Context Menu Entry” 即可 Notepad的右击打开文件功能 默认已勾选 其作用是添加右键快捷键。即,对于任何…...

JSON.parseObject强制将自动转化的Intage型设置为Long型
通过Redis或Caffeine存储入json型String,通过JSON.parseObject自动类型转化之后,数值会优先转为Intage,如果存入的字符值大于Intage最大值,会自动转为Long型; 需求是:实要取出时数值类型值为Long࿱…...

Redis的集群模式:主从 哨兵 分片集群
基于Redis集群解决单机Redis存在的问题,在之前学Redis一直都是单节点部署 单机或单节点Redis存在的四大问题: 数据丢失问题:Redis是内存存储,服务重启可能会丢失数据 > 利用Redis数据持久化的功能将数据写入磁盘并发能力问题…...
Note: An Interesting Festival
An Interesting Festival 一个有趣的节日。 festival The Agricultural Feast takes place after the independence Day. 农业盛会在独立日后举行 takes place independence feast agricultural It is not a worldwide celebration. 它不是一个全球的庆典。 worldwide ce…...
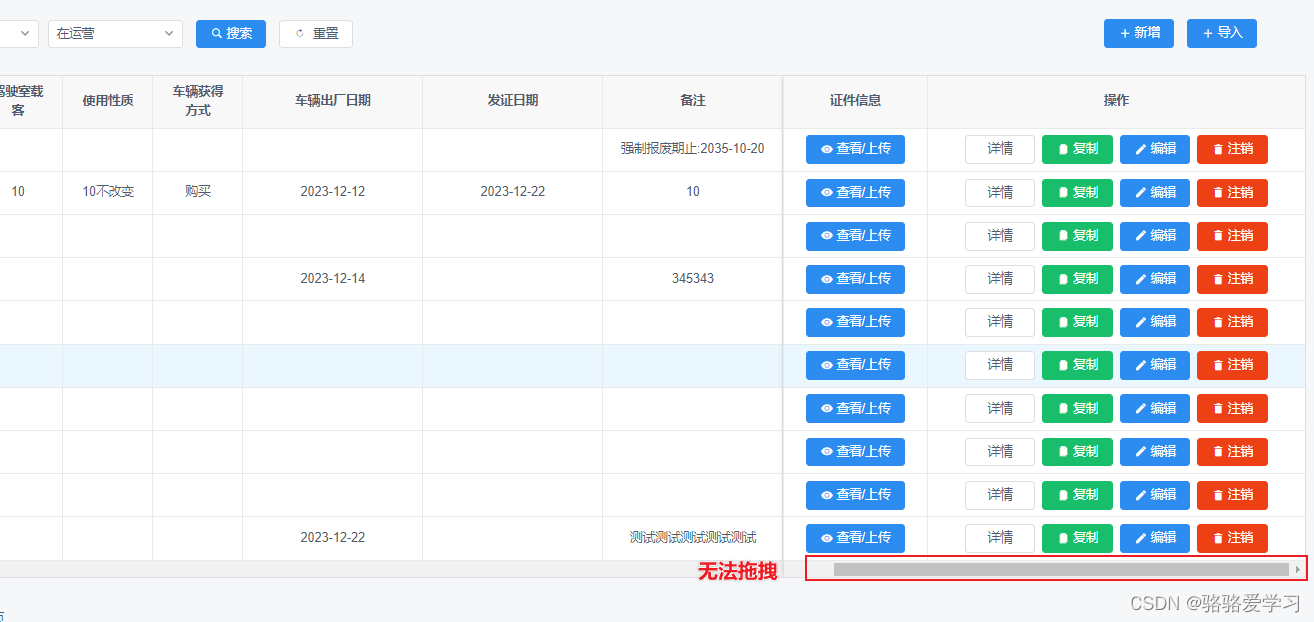
iview表格固定列横向滚动条无法拖动问题
文章目录 问题解决办法 问题 在使用iview的表格组件时,遇到了设置固定列表格后滚动条无法拖动的问题,当对表格列进行固定后,底部的横向滚动条就无法拖动了,主要的问题就是固定区域盖住了横向滚动条。 解决办法 在组件内直接加下…...

Python序列之集合
系列文章目录 Python序列之列表Python序列之元组Python序列之字典Python序列之集合(本篇文章) Python序列之集合 系列文章目录前言一、集合是什么?二、集合的操作1.集合的创建(1)使用{}创建(2)…...

智慧园区物联综合管理平台之架构简述
总体架构 系统总体划分为物联感知系统层、 核心平台层、 综合运营服务平台和展示层四部分。 物联感知系统层 物联感知系统主要是支撑园区智能化运行的各子系统, 包括门禁系统、 视频监控系统、 车辆管理系统等。 核心平台层 核心平台层包括: 园区物联综合管理平台和园区…...

国科大图像处理2023速通期末——汇总2017-2019
国科大2023.12.28图像处理0854期末重点 图像处理 王伟强 作业 课件 资料 一、填空 一个阴极射线管它的输入与输出满足 s r 2 sr^{2} sr2,这将使得显示系统产生比希望的效果更暗的图像,此时伽马校正通常在信号进入显示器前被进行预处理,令p…...
oracle 9i10g编程艺术-读书笔记2
配置Statspack 安装Statspack需要用internal身份登陆,或者拥有SYSDBA(connect / as sysdba)权限的用户登陆。需要在本地安装或者通过telnet登陆到服务器。 select instance_name,host_name,version,startup_time from v$instance;检查数据文件路径及磁盘空间&…...

PACC:数据中心网络的主动 CNP 生成方案
PACC:数据中心网络的主动 CNP 生成方案 文章目录 PACC:数据中心网络的主动 CNP 生成方案PACC算法CNP数据结构PACC参数仿真结果参考文献 PACC算法 CNP数据结构 PACC参数 仿真结果 PACC Hadoop Load0.2 的情况: PACC Hadoop Load0.4 的情况&a…...

我最喜欢的趣味几何书-读书笔记
我最喜欢的趣味几何书-读书笔记 1、利用阴影的长度来测量 公元前6世纪,古希腊哲学家泰勒思为了测量金字塔,想到了这样的方法:选择了一个特殊的时间,在那个时间,他自身的影子长度刚好跟他的身高相等。此时,…...
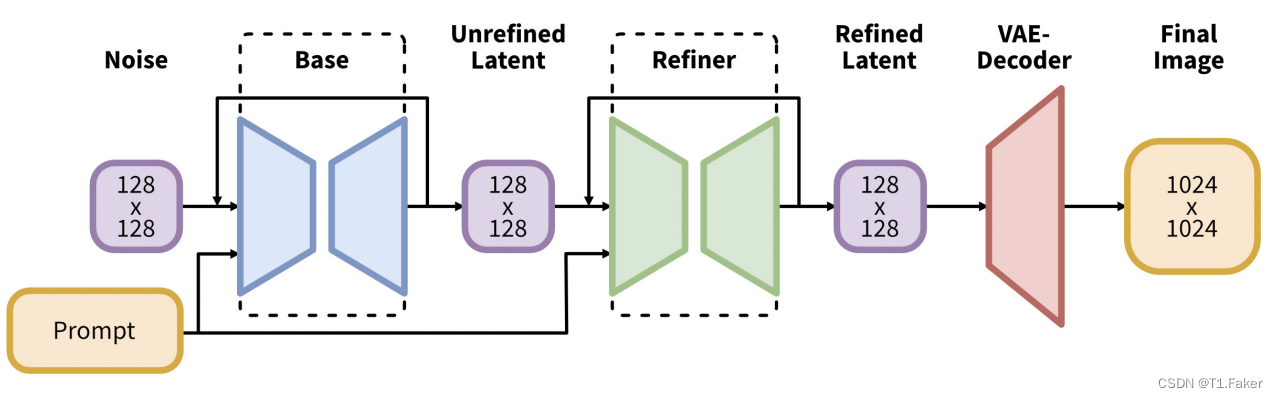
Stable Diffusion模型概述
Stable Diffusion 1. Stable Diffusion能做什么?2. 扩散模型2.1 正向扩散2.2 反向扩散 3. 训练如何进行3.1 反向扩散3.2 Stable Diffusion模型3.3 潜在扩散模型3.4 变分自动编码器3.5 图像分辨率3.6 图像放大 4. 为什么潜在空间是可能的?4.1 在潜在空间中…...

二叉树详解(深度优先遍历、前序,中序,后序、广度优先遍历、二叉树所有节点的个数、叶节点的个数)
目录 一、树概念及结构(了解) 1.1树的概念 1.2树的表示 二、二叉树概念及结构 2.1概念 2.2现实中的二叉树: 2.3数据结构中的二叉树: 2.4特殊的二叉树: 2.5 二叉树的存储结构 2.51 顺序存储: 2.5.2 链式存储&…...
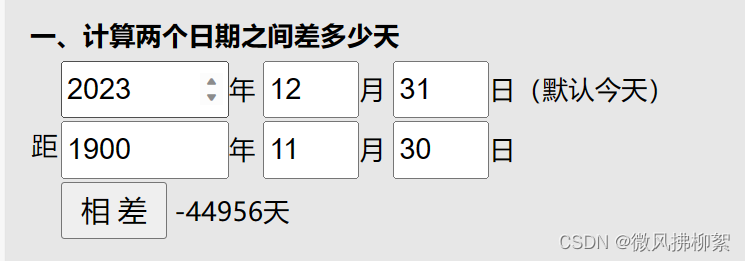
C++日期类的实现
前言:在类和对象比较熟悉的情况下,我们我们就可以开始制作日期表了,实现日期类所包含的知识点有构造函数,析构函数,函数重载,拷贝构造函数,运算符重载,const成员函数 1.日期类的加减…...

B+树的插入删除
操作 插入 case2的原理,非叶子节点永远和最右边的最左边的节点的值相等。 case3:的基本原理 非叶子节点都是索引节点 底层的数据分裂之后 相当于向上方插入一个新的索引(你可以认为非叶子节点都是索引),反正第二层插入160 都要分裂,然后也需要再插入(因为索引部分不需要重…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
