Python序列之集合
系列文章目录
- Python序列之列表
- Python序列之元组
- Python序列之字典
- Python序列之集合(本篇文章)
Python序列之集合
- 系列文章目录
- 前言
- 一、集合是什么?
- 二、集合的操作
- 1.集合的创建
- (1)使用`{}`创建
- (2)使用`set()`函数创建
- 2.集合元素的添加
- (1)使用`add()`添加单个元素
- (2)使用`update()`批量添加元素
- 3.集合元素的删除
- (1)使用`remove()`删除指定元素
- (2)使用`discard()`删除指定元素
- (3)使用`clear()`清空整个集合
- (4)使用`pop()`随机弹出一个元素
- 4.使用集合去重(重要应用)
- 5.集合的数学运算
- (1)交集
- (2)并集
- (3)差集(补集)
- (4)对称差集
- (5)判断是否为子集、母集
- 总结
前言
前面我们已经讲了Python中的列表:Python序列之列表、元组:Python序列之元组和字典:Python序列之字典。今天我们再来看一下Python中另一种序列——集合。
集合这个词大家肯定不陌生,高中数学必修一第一章,便是集合。你应该还记得数学老师说过:“集合具有三个性质:确定性、互异性、无序性”,Python中的集合set便是借鉴了数学中的这种“数据结构”。同样满足这三个性质。
不仅如此,Python还提供的数学中集合的各种运算:求并集、求交集、求补集……
一、集合是什么?
集合是无序可变的,元素不能重复,故经常用集合来实现数据去重。实际上,集合底层是字典实现,集合的所有元素都是字典中的"键对象",因此是不能重复的且唯一的。

二、集合的操作
1.集合的创建
(1)使用{}创建
a = {3, 5, 7}
b = {} # 创建一个空集合
c = {3} # 只有一个元素的集合
print(a) # 输出:{3, 5, 7}
print(b) # 输出:{}
print(c) # 输出:{3}
(2)使用set()函数创建
a = ['a', 2, True]
b = set(a)
c = set() # 创建一个空集合print(b) # 输出:{True, 'a', 2}
print(c) # 输出:set()
print(type(b)) # 输出:<class 'set'>
print(type(c)) # 输出:<class 'set'>
由上面的两个例子可知,Python对空集合的打印表示有两种:{}和set()。
2.集合元素的添加
(1)使用add()添加单个元素
a = {10, 20, 30}
a.add('a')
print(a) # 输出:{10, 'a', 20, 30}
(2)使用update()批量添加元素
a = {10, 20, 30}
b = [True, False, 999]
a.update(b)
print(a) # 输出:{False, True, 999, 10, 20, 30}
3.集合元素的删除
(1)使用remove()删除指定元素
a = {10, 20, 30, 40, 50}
a.remove(30)
print(a) # 输出:{50, 20, 40, 10}
a.remove(999) # 报错:KeyError: 999
可以发现,当试图用remove()移除一个集合中并不存在的元素时,解释器会报错。这种反应过于暴力,因此有了更加温柔且绅士的删除方法——discard()。
(2)使用discard()删除指定元素
a = {10, 20, 30, 40, 50}
a.remove(30)
print(a) # 输出:{50, 20, 40, 10}
a.discard(999) # 无报错
print(a) # 输出:{50, 20, 40, 10}
当试图删除一个集合中并不存在的元素时,discard()并不会报错,而是什么都不干,程序照常往下运行,优雅且绅士~
(3)使用clear()清空整个集合
a = {10, 20, 30, 40, 50}
a.clear()
print(a) # 输出:set()
(4)使用pop()随机弹出一个元素
a = {10, 20, 30, 40, 50}
b = a.pop()
print(b) # 输出:50
print(a) # 输出:{20, 40, 10, 30}
4.使用集合去重(重要应用)
我们可以充分利用集合的互异性来实现列表元素的去重:
a = [1, 1, 5, 6, 6, 8, 9, 8, 6]
b = set(a)
print(b) # 输出:{1, 5, 6, 8, 9}
5.集合的数学运算
像数学中概念一样,Python对集合也提供了并集、交集、差集等运算。

(1)交集

下面展式了三种取交集的方法:
a = {1, 2, 3, 4}
b = {2, 3, 99, 100, 'yyy'}c = a & b # 方法一:&
print(c) # 输出:{2, 3}d = a.intersection(b) # 方法二:取交集并返回一个新集合
print(d) # 输出:{2, 3}print(a) # 输出:{1, 2, 3, 4}
a.intersection_update(b) # 方法三:取交集并更新原集合
print(a) # 输出:{2, 3}
(2)并集

下面展式了两种取并集的方法:
a = {1, 2, 3, 4}
b = {2, 3, 99, 100, 'yyy'}c = a | b # 方法一:|
print(c) # 输出:{1, 2, 3, 4, 99, 100, 'yyy'}d = a.union(b) # 方法二:union()
print(d) # 输出:{1, 2, 3, 4, 99, 100, 'yyy'}
(3)差集(补集)

下面展式了三种取差集的方法:
a = {1, 2, 3, 4}
b = {2, 3, 99, 100, 'yyy'}c = a - b # 方法一:-
print(c) # 输出:{1, 4}d = a.difference(b) # 方法二:取交集并返回一个新集合
print(d) # 输出:{1, 4}print(a) # 输出:{1, 2, 3, 4}
a.difference_update(b) # 方法三:取交集并更新原集合
print(a) # 输出:{1, 4}
注意:差集是有方向性的,A-B ≠ B-A
(4)对称差集

python集合set内置方法symmetric_differece(),可以用来返回两个集合(或调用对象集合与其它可迭代对象iterable)中非共同的元素组成的新集合set。
a = {1, 2, 3, 4}
b = {2, 3, 99, 100, 'yyy'}c = a ^ b # 方法一:^
print(c) # 输出:{1, 99, 100, 'yyy', 4}d = a.symmetric_difference(b) # 方法二:取对称差并返回一个新集合
print(d) # 输出:{1, 99, 100, 4, 'yyy'}print(a) # 输出:{1, 2, 3, 4}
a.symmetric_difference_update(b) # 方法三:取对称差并更新原集合
print(a) # 输出:{1, 99, 100, 4, 'yyy'}
(5)判断是否为子集、母集
| 方法 | 用途 |
|---|---|
a.issubset(b) | 判断a是否为b的子集 |
a.issuperset(b) | 判断a是否为b的母集 |
a.isdisjoint(b) | 判断a与b的交集是否为空集 |
a = {1, 2, 3}
b = {1, 2, 3, 4, 5}
c = {1, 2, 'yyy'}
d = {'a', 'b', 'c'}print(a.issubset(b)) # 输出:True
print(a.issubset(c)) # 输出:Falseprint(b.issuperset(a)) # 输出:Trueprint(a.isdisjoint(c)) # 输出:False
print(a.isdisjoint(d)) # 输出:True
总结
Python中的集合可以认为是数学中集合的具体实现,具有数学集合的三个性质,不仅可以进行增删改查,还可以进行数学中的集合运算。
相关文章:

Python序列之集合
系列文章目录 Python序列之列表Python序列之元组Python序列之字典Python序列之集合(本篇文章) Python序列之集合 系列文章目录前言一、集合是什么?二、集合的操作1.集合的创建(1)使用{}创建(2)…...

智慧园区物联综合管理平台之架构简述
总体架构 系统总体划分为物联感知系统层、 核心平台层、 综合运营服务平台和展示层四部分。 物联感知系统层 物联感知系统主要是支撑园区智能化运行的各子系统, 包括门禁系统、 视频监控系统、 车辆管理系统等。 核心平台层 核心平台层包括: 园区物联综合管理平台和园区…...

国科大图像处理2023速通期末——汇总2017-2019
国科大2023.12.28图像处理0854期末重点 图像处理 王伟强 作业 课件 资料 一、填空 一个阴极射线管它的输入与输出满足 s r 2 sr^{2} sr2,这将使得显示系统产生比希望的效果更暗的图像,此时伽马校正通常在信号进入显示器前被进行预处理,令p…...
oracle 9i10g编程艺术-读书笔记2
配置Statspack 安装Statspack需要用internal身份登陆,或者拥有SYSDBA(connect / as sysdba)权限的用户登陆。需要在本地安装或者通过telnet登陆到服务器。 select instance_name,host_name,version,startup_time from v$instance;检查数据文件路径及磁盘空间&…...

PACC:数据中心网络的主动 CNP 生成方案
PACC:数据中心网络的主动 CNP 生成方案 文章目录 PACC:数据中心网络的主动 CNP 生成方案PACC算法CNP数据结构PACC参数仿真结果参考文献 PACC算法 CNP数据结构 PACC参数 仿真结果 PACC Hadoop Load0.2 的情况: PACC Hadoop Load0.4 的情况&a…...

我最喜欢的趣味几何书-读书笔记
我最喜欢的趣味几何书-读书笔记 1、利用阴影的长度来测量 公元前6世纪,古希腊哲学家泰勒思为了测量金字塔,想到了这样的方法:选择了一个特殊的时间,在那个时间,他自身的影子长度刚好跟他的身高相等。此时,…...
Stable Diffusion模型概述
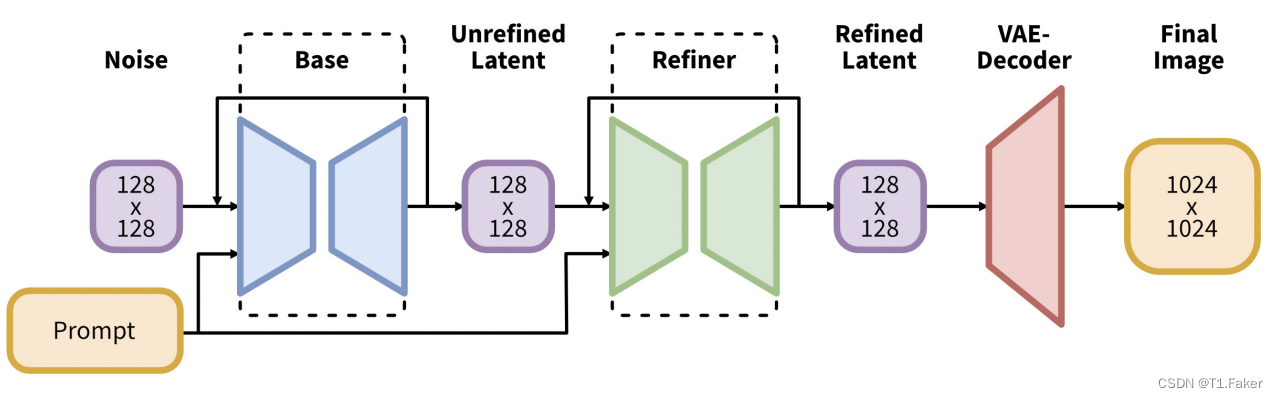
Stable Diffusion 1. Stable Diffusion能做什么?2. 扩散模型2.1 正向扩散2.2 反向扩散 3. 训练如何进行3.1 反向扩散3.2 Stable Diffusion模型3.3 潜在扩散模型3.4 变分自动编码器3.5 图像分辨率3.6 图像放大 4. 为什么潜在空间是可能的?4.1 在潜在空间中…...

二叉树详解(深度优先遍历、前序,中序,后序、广度优先遍历、二叉树所有节点的个数、叶节点的个数)
目录 一、树概念及结构(了解) 1.1树的概念 1.2树的表示 二、二叉树概念及结构 2.1概念 2.2现实中的二叉树: 2.3数据结构中的二叉树: 2.4特殊的二叉树: 2.5 二叉树的存储结构 2.51 顺序存储: 2.5.2 链式存储&…...
C++日期类的实现
前言:在类和对象比较熟悉的情况下,我们我们就可以开始制作日期表了,实现日期类所包含的知识点有构造函数,析构函数,函数重载,拷贝构造函数,运算符重载,const成员函数 1.日期类的加减…...

B+树的插入删除
操作 插入 case2的原理,非叶子节点永远和最右边的最左边的节点的值相等。 case3:的基本原理 非叶子节点都是索引节点 底层的数据分裂之后 相当于向上方插入一个新的索引(你可以认为非叶子节点都是索引),反正第二层插入160 都要分裂,然后也需要再插入(因为索引部分不需要重…...

c# Avalonia 绘图
在Avalonia UI框架中,绘图主要通过使用DrawingContext类来实现。DrawingContext提供了一系列的绘图API,可以用来绘制线条、形状、图像以及文本等内容。以下是一个简单的示例,说明如何在Avalonia中进行基础的图形绘制 <!-- MainWindow.axa…...

springboot 双数据源配置
1:pom <!--SpringBoot启动依赖--><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency><dependency><groupId>org.springframework.boot</group…...
Redis内存使用率高,内存不足问题排查和解决
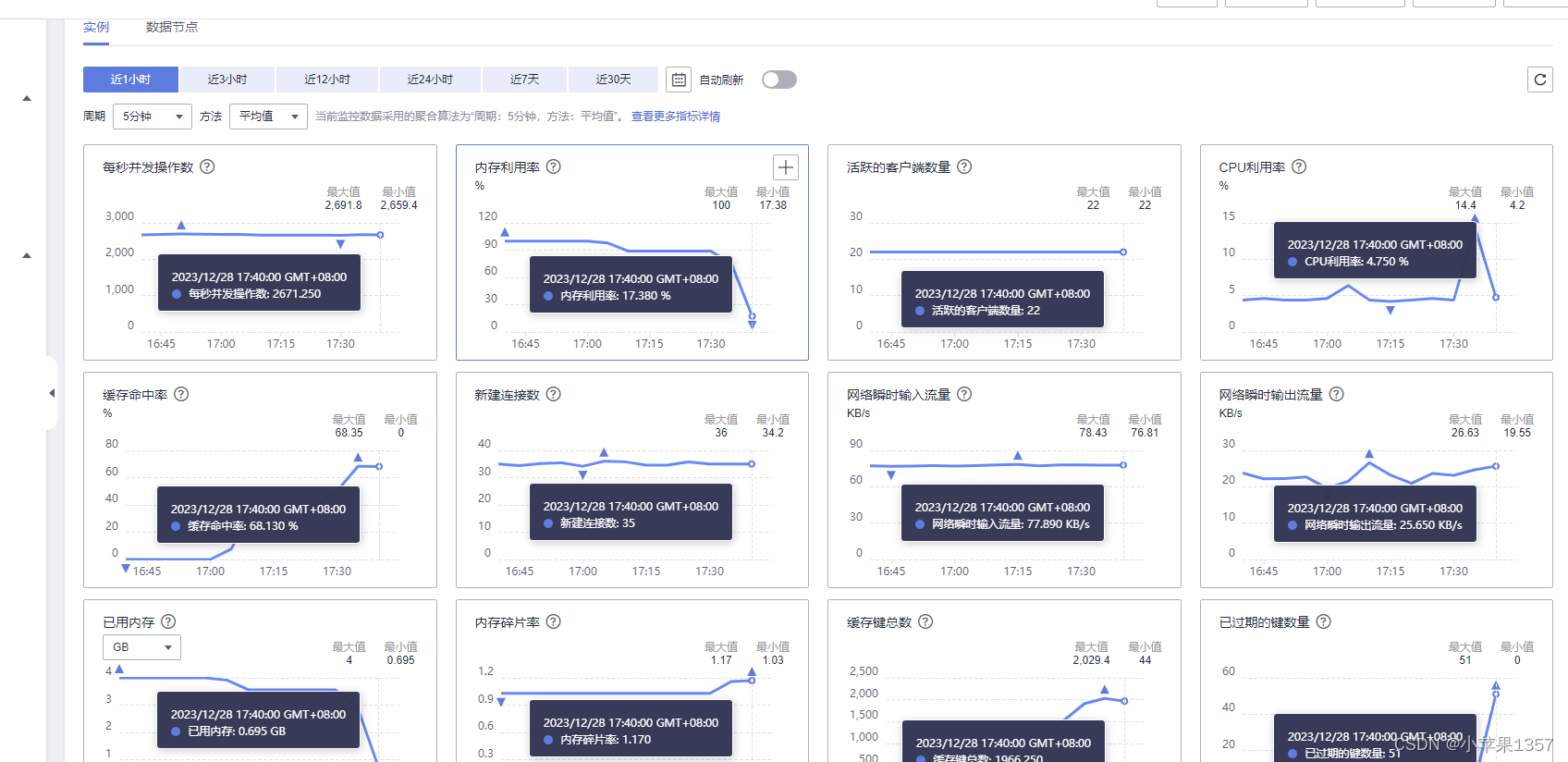
问题现象 表面现象是系统登录突然失效,排查原因发现,使用redis查询用户信息异常,从而定位到redis问题 if (PassWord.equals(dbPassWord)) {map.put("rtn", 1);map.put("value", validUser);session.setAttribute("…...
bootstrap5开发房地产代理公司Hamilton前端页面
一、需求分析 房地产代理网站是指专门为房地产行业提供服务的在线平台。这些网站的主要功能是连接房地产中介机构、房产开发商和潜在的买家或租户,以促成买卖或租赁房产的交易。以下是一些常见的房地产代理网站的功能: 房源发布:房地产代理网…...
2024年Mac专用投屏工具AirServer 7 .27 for Mac中文版
AirServer 7 .27 for Mac中文免费激活版是一款Mac专用投屏工具,能够通过本地网络将音频、照片、视频以及支持AirPlay功能的第三方App,从 iOS 设备无线传送到 Mac 电脑的屏幕上,把Mac变成一个AirPlay终端的实用工具。 目前最新的AirServer 7.2…...

关于MySql字段类型的实践总结
当字段为数值类型时应使用无符号UNSIGNED修饰 ALTER TABLE infoMODIFY COLUMN user_id int UNSIGNED NOT NULL; 当字段为varchar类型时应注意是否选择合适的字符集 例如存储一些范围值,数字英文字符时(IP、生日、客户端标识等或以“,”分隔的数据&…...
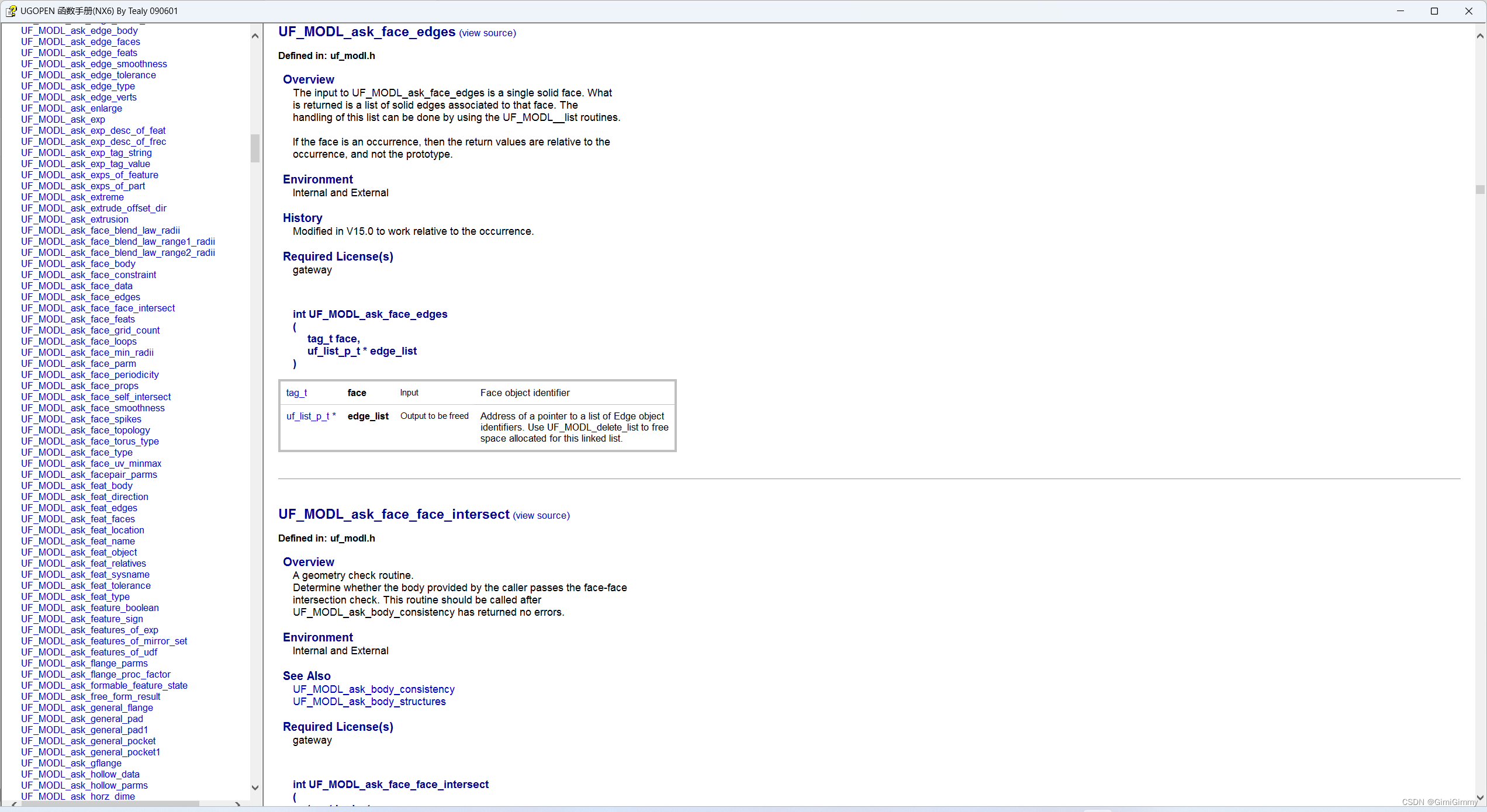
UG NX二次开发(C#)-Ufun和NXOpen混合编程
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1、前言2、Ufun函数3、 NXOpen4、混合编程实现1、前言 在UG NX二次开发过程中,采用Ufun功能比较简单,能用比较少的代码实现我们需要的功能,但是ufun函数的功能不是很强大,尤其随着UG NX的版本…...
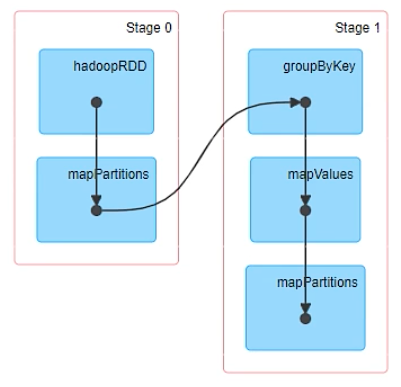
【Spark精讲】一文讲透Spark RDD
MapReduce的缺陷 MR虽然在编程接口的种类和丰富程度上已经比较完善了,但这些系统普遍都缺乏操作分布式内存的接口抽象,导致很多应用在性能上非常低效 。 这些应用的共同特点是需要在多个并行操 作之间重用工作数据集 ,典型的场景就是机器学习…...

如在MT9040、IDT82V3001A 等锁相环上电后或输入参考频率改变后必须复位锁相环。
锁相环是一种反馈控制系统,它能够将输出信号的相位锁定到输入参考信号的相位上。在实际应用中,如MT9040、IDT82V3001A等PLL集成电路在上电后或者当输入参考频率发生变化后通常需要复位的原因涉及到几个方面: 1、初始化状态: 当PLL电路上电时,其内部的各个组件可能…...

构建安全的SSH服务体系
某公司的电子商务站点由专门的网站管理员进行配置和维护,并需要随时从Internet进行远程管理,考虑到易用性和灵活性,在Web服务器上启用OpenSSH服务,同时基于安全性考虑,需要对 SSH登录进行严格的控制,如图10…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
