堆排序(C语言版)
一.堆排序
1.1.利用上下调整法实现堆排序
第一步:建堆
好了,每次建堆都要问自己下,要建的是什么堆?大堆还是小堆呢?
我们这里就一一来实现,先建大堆
void Print(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}
void Swap(int* p1, int* p2)
{int* tmp = *p1;* p1=*p2;*p2 = tmp;
}
void Adjustup(int* arr2, int child)
{int parent = (child - 1) / 2;while (child > 0){if (arr2[child]>arr2[parent])//注意我们是建的大堆{Swap(&arr2[child], &arr2[parent]);//传地址才能改变值child = parent;parent = (child - 1) / 2;}else{break;}}
}
void Heapsort(int* arr, int n)
{//建立堆//问题是:你是建大堆还是小堆?//我们这里要建大堆for (int i = 1; i < n; i++){Adjustup(arr, i);//利用向上调整法}Print(arr,n);
}如果你实现过堆的代码相信上面的代码对你来说绝对小菜一碟
由于我们直接调用了打印函数,那么我们来看看结果吧。
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
void Print(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}
void Swap(int* p1, int* p2)
{int* tmp = *p1;* p1=*p2;*p2 = tmp;
}
void Adjustup(int* arr2, int child)
{int parent = (child - 1) / 2;while (child > 0){if (arr2[child]>arr2[parent])//注意我们是建的大堆{Swap(&arr2[child], &arr2[parent]);//传地址才能改变值child = parent;parent = (child - 1) / 2;}else{break;}}
}
void Heapsort(int* arr, int n)
{//建立堆//问题是:你是建大堆还是小堆?//我们这里要建大堆for (int i = 1; i < n; i++){Adjustup(arr, i);//利用向上调整法}Print(arr,n);
}
int main()
{int arr[] = { 4,6,2,1,5,8,2,9 };int sz = sizeof(arr) / sizeof(int);Heapsort(arr, sz);return 0;
}结果:

这个是不是就满足了大堆
第二步:如何实现排序呢?(别看上面是从大到小排好的,这只是一个巧合,我们要学会正确的排序法)
如果你对此不清楚,那么我要开始表演了。
如果你想,我们是大堆,这说明最大的数即是堆顶,如果我交换数组首尾位置,然后这是不是不再是一颗完全二叉树了,那么如果我再通过向下调整法来排好,重复操作,是不是就会得到一个从小到大的数组,那么不就排好序了,想到这,相信你肯定联想到了堆的删除操作,下面就让我们利用堆的删除来实现它吧!
void Swap(int* p1, int* p2)
{int* tmp = *p1;* p1=*p2;*p2 = tmp;
}
void Adjustdown(int* arr3, int n, int parent)
{int child = parent * 2 + 1;//假设左孩子大//注意我们建的是大堆while (child < n){if ((child + 1) < n && (arr3[child] < arr3[child + 1])){child++;}if (arr3[parent] < arr3[child]){Swap(&arr3[parent], &arr3[child]);//交换父子位置parent = child;child = parent * 2 + 1;}else{break;}}
}//堆建好了,现在实现第二步:堆删除
int end = n - 1;
while (end > 0)
{//堆删除分以下几步://第一步:首尾元素互换Swap(&arr[0], &arr[end]);//第二步:向下调整法调整树根Adjustdown(arr, end, 0);//第三步:删除堆尾end--;
}这对于学过实现堆的你来说依然so easy。
那么就让我们整体检查代码的正确性:
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
void Print(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}
void Swap(int* p1, int* p2)
{int* tmp = *p1;* p1=*p2;*p2 = tmp;
}
void Adjustup(int* arr2, int child)
{int parent = (child - 1) / 2;while (child > 0){if (arr2[child]>arr2[parent])//注意我们是建的大堆{Swap(&arr2[child], &arr2[parent]);//传地址才能改变值child = parent;parent = (child - 1) / 2;}else{break;}}
}
void Adjustdown(int* arr3, int n, int parent)
{int child = parent * 2 + 1;//假设左孩子大//注意我们建的是大堆while (child < n){if ((child + 1) < n && (arr3[child] < arr3[child + 1])){child++;}if (arr3[parent] < arr3[child]){Swap(&arr3[parent], &arr3[child]);//交换父子位置parent = child;child = parent * 2 + 1;}else{break;}}
}
void Heapsort(int* arr, int n)
{//建立堆//问题是:你是建大堆还是小堆?//我们这里要建大堆for (int i = 1; i < n; i++){Adjustup(arr, i);//利用向上调整法}Print(arr,n);//堆建好了,现在实现第二步:堆删除int end = n - 1;while (end > 0){//堆删除分以下几步://第一步:首尾元素互换Swap(&arr[0], &arr[end]);//第二步:向下调整法调整树根Adjustdown(arr, end, 0);//第三步:删除堆尾end--;}Print(arr, n);
}
int main()
{int arr[] = { 4,6,2,1,5,8,2,9 };int sz = sizeof(arr) / sizeof(int);Heapsort(arr, sz);return 0;
}结果:
如果你是要从大到小排序,操作如下:
建小堆-》堆的尾删
整体而言有三处改动:
1.在void Adjustup(int* arr2, int child)函数中这个语句要改变符号,因为是建小堆了。
if (arr2[child]>arr2[parent])//
2.在void Adjustdown(int* arr3, int n, int parent)这个函数中这两处符号也要改变,原因是因为你现在是小堆,向下调整法肯定要调整
if (arr3[child] < arr3[child + 1]))
if (arr3[parent] < arr3[child])
整体如下:
//表示原来的语句//arr2[child]>arr2[parent]
arr2[child]<arr2[parent]//if ((child + 1) < n && (arr3[child] < arr3[child + 1]))
if ((child + 1) < n && (arr3[child] > arr3[child + 1]))//if (arr3[parent] < arr3[child])
if (arr3[parent] > arr3[child])改完之后结果如下:

现在我们就要对这个算法进行分析:
时间复杂度:建堆为O(NlogN)+选数O(N-1logN)
得出结果:O(NlogN)(非常牛逼的算法)
1.2.只利用向下调整法实现堆排序
大家看上面的代码是不是感觉一个排序要写这么麻烦好不方便啊,是的,我们其实可以只通过一个向下调整就可以实现堆排序,下面看看我的表演吧!
步骤还是和上面一样,其实就改变了建堆的过程,我们现在是通过向下调整法建堆。
看代码:
for (int i = ; i ; i)
{Adjustdown(arr,,);
}我们就是要把上面的空缺填好,那么该如何写呢?
我要告诉你一个概念:向下调整建堆是从第一个非叶子节点开始调整,我们肯定要调整到0
所以我们可以这样写:
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{Adjustdown(arr,n,i);
}其他部分不用改变,所以整体代码如下:
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
void Print(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}
void Swap(int* p1, int* p2)
{int* tmp = *p1;* p1=*p2;*p2 = tmp;
}
void Adjustdown(int* arr3, int n, int parent)
{int child = parent * 2 + 1;//假设左孩子大//注意我们建的是大堆while (child < n){if ((child + 1) < n && (arr3[child] < arr3[child + 1])){child++;}if (arr3[parent] < arr3[child]){Swap(&arr3[parent], &arr3[child]);//交换父子位置parent = child;child = parent * 2 + 1;}else{break;}}
}
void Heapsort(int* arr, int n)
{for (int i = (n - 1 - 1) / 2; i >= 0; i--){Adjustdown(arr,n,i);}Print(arr, n);//堆建好了,现在实现第二步:堆删除int end = n - 1;while (end > 0){//堆删除分以下几步://第一步:首尾元素互换Swap(&arr[0], &arr[end]);//第二步:向下调整法调整树根Adjustdown(arr, end, 0);//第三步:删除堆尾end--;}Print(arr, n);
}
int main()
{int arr[] = { 4,6,2,1,5,8,2,9 };int sz = sizeof(arr) / sizeof(int);Heapsort(arr, sz);return 0;
}结果:
来我们该讨论该算法时间复杂度情况了
建堆O(N)+选数O(NlogN)
时间复杂度:O(N*logN)
注意:该写法不仅简单(比上面那种),而且效率也比上面的高。
相关文章:

堆排序(C语言版)
一.堆排序 堆排序即利用堆的思想来进行排序,总共分为两个步骤: 1. 建堆 升序:建大堆 降序:建小堆 2. 利用堆删除思想来进行排序 1.1.利用上下调整法实现堆排序 第一步:建堆 好了,每次建堆都要问自己…...
实现区域地图散点图效果,vue+echart地图+散点图
需求:根据后端返回的定位坐标数据实现定位渲染 1.效果图 2.准备工作,在main.js和index.js文件中添加以下内容 main.js app.use(BaiduMap, {// ak 是在百度地图开发者平台申请的密钥 详见 http://lbsyun.baidu.com/apiconsole/key */ak: sRDDfAKpCSG5iF1rvwph4Q95M…...
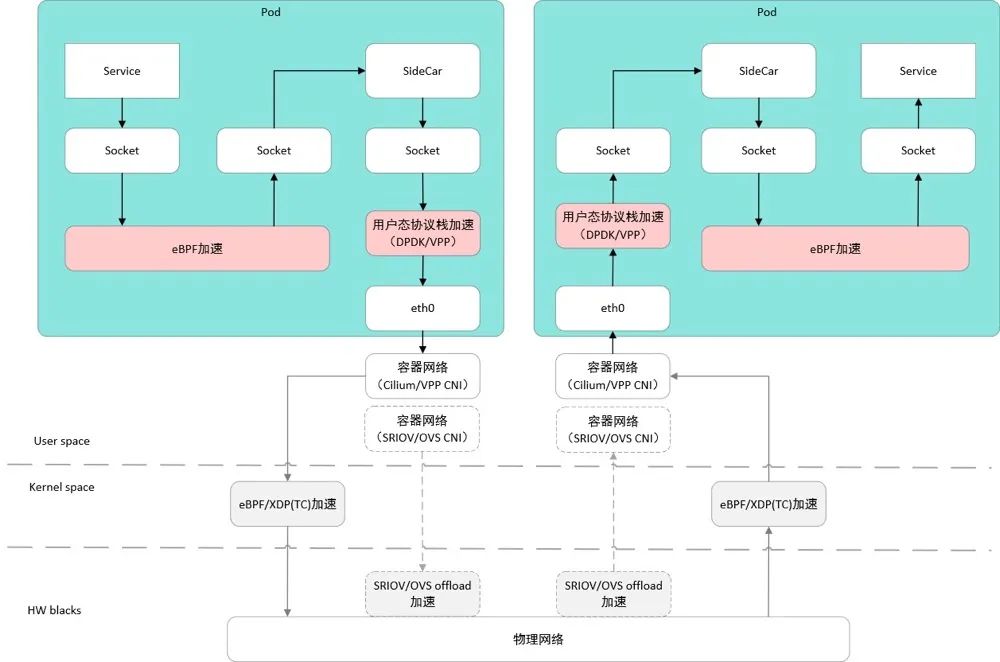
Kubernetes 学习总结(41)—— 云原生容器网络详解
背景 随着网络技术的发展,网络的虚拟化程度越来越高,特别是云原生网络,叠加了物理网络、虚机网络和容器网络,数据包在网络 OSI 七层网络模型、TCP/IP 五层网络模型的不同网络层进行封包、转发和解包。网络数据包跨主机网络、容器…...
多人协同开发git flow,创建初始化项目版本
文章目录 多人协同开发git flow,创建初始化项目版本1.gitee创建组织模拟多人协同开发2.git tag 打标签3.git push origin --tags 多人协同开发git flow,创建初始化项目版本 1.gitee创建组织模拟多人协同开发 组织中新建仓库 推送代码到我们组织的仓库 2…...

「Kafka」入门篇
「Kafka」入门篇 基础架构 Kafka 快速入门 集群规划 集群部署 官方下载地址:http://kafka.apache.org/downloads.html 解压安装包: [atguiguhadoop102 software]$ tar -zxvf kafka_2.12-3.0.0.tgz -C /opt/module/修改解压后的文件名称: [a…...
编译器是什么?)
PHP8的JIT(Just-In-Time)编译器是什么?
PHP8的JIT(Just-In-Time)编译器是什么? PHP8是最新的PHP版本,引入了JIT(Just-In-Time)编译器,以进一步提高性能和执行速度。 JIT编译器是一种在运行时将解释性语言转化为机器码的技术。在过去…...

【C++对于C语言的扩充】C++与C语言的联系,命名空间、C++中的输入输出以及缺省参数
文章目录 🚀前言🚀C有何过C之处?🚀C中的关键字🚀命名空间✈️为什么要引入命名空间?✈️命名空间的定义✈️如何使用命名空间中的内容呢? 🚀C中的输入和输出✈️C标准库的命名空间✈…...
Excel中部分sheet页隐藏并设置访问密码
1、新建sheet1 2、新建sheet2 3、隐藏sheet2 4、保护工作簿、输密码 5、密码二次确认 6、隐藏的sheet2已经查看不了 7、想要查看时,按图示输入原密码即可 8、查看sheet2内容...
从零开始配置pwn环境:CTF PWN 做题环境
前期在kali2023环境安装的pwndocker使用发现不好用,so找了网上配置好pwn环境的虚拟机。 GitHub - giantbranch/pwn-env-init: CTF PWN 做题环境一键搭建脚本 可以直接下载我配置好的Ubuntu 16.04,为VMware导出的ovf格式 链接:百度网盘 请输…...

Vue3复习笔记
目录 挂载全局属性和方法 v-bind一次绑定多个值 v-bind用在样式中 Vue指令绑定值 Vue指令绑定属性 动态属性的约束 Dom更新时机 ”可写的“计算属性 v-if与v-for不建议同时使用 v-for遍历对象 数组变化检测 事件修饰符 v-model用在表单类标签上 v-model还可以绑定…...
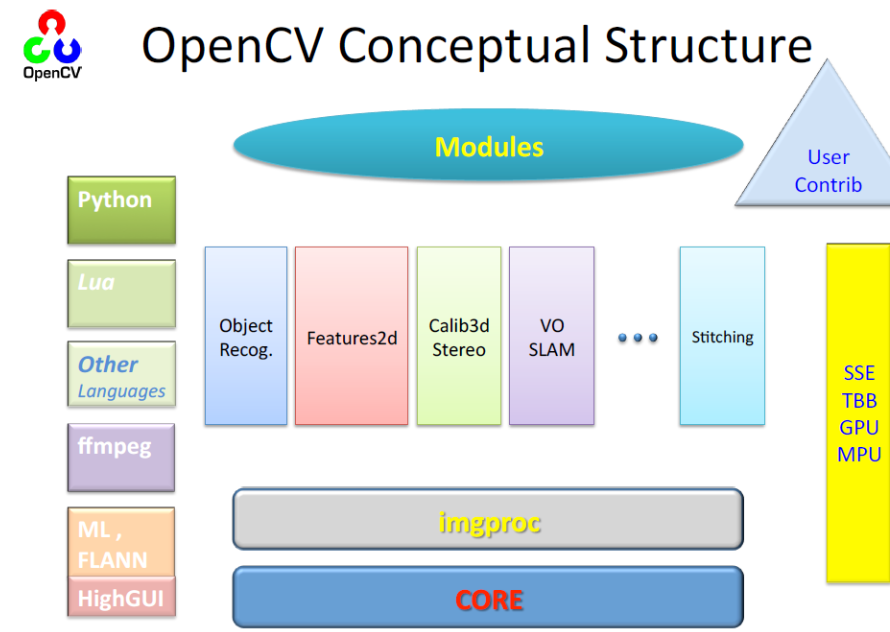
【OpenCV】OpenCV:计算机视觉的强大工具库
摘要 OpenCV是一个广泛应用于计算机视觉领域的开源工具库,为开发者提供了丰富的图像处理和计算机视觉算法。本文将介绍OpenCV的功能和应用领域,并探讨它在实践中的重要性和前景。 计算机视觉的强大工具库 一、什么是OpenCV?二、OpenCV的功…...
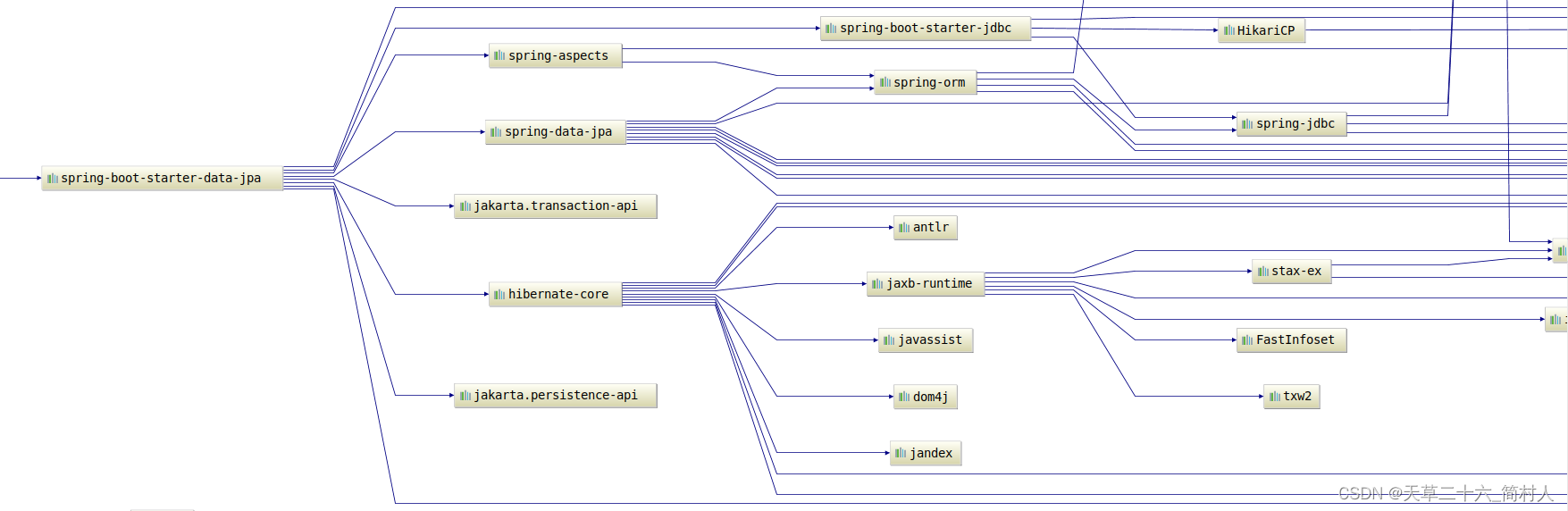
spring-boot-autoconfigure误引入spring-boot-starter-data-jpa而导致数据源初始化异常
一、现状描述 某个Grade类引入了jpa的注解: import javax.persistence.Column; import javax.persistence.Embeddable;/*** 年级*/ Embeddable public class Grade {Column(name "code")private int code; }并且pom.xml中引入该jar包:sprin…...

工程(十六)——自己数据集跑Fast_livo
一、基础环境 Ubuntu20.04 ROS noetic PCL 1.8 Eigen 3.3.4 Sophus git clone https://github.com/strasdat/Sophus.git cd Sophus git checkout a621ff mkdir build && cd build && cmake .. make sudo make install 下面两个直接把包下载下来一起编译…...
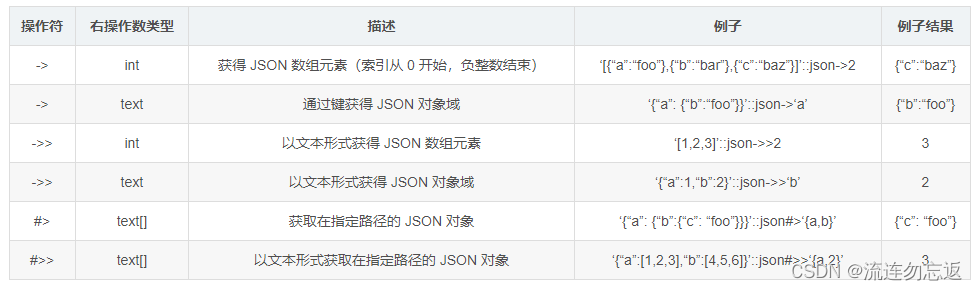
PostgreSQL数据库的json操作
1.操作符 select json字段::json->key值 from order -- 对象域 select json字段::json->>key值 from order -- 文本 select json字段::json#>{key值} from order -- 对象域 select json字段::json#>>{key值} from order -- 文本对象域表示还能继续操作&#…...

gradio-osprey-demo
创建需要的dockerfle ################### # 使用 Ubuntu 作为基础镜像 FROM nvcr.io/nvidia/cuda:11.8.0-devel-ubuntu22.04 # 更新软件包列表并安装依赖项 RUN apt update && \ apt install -y python3 python3-pip git ffmpeg libsm6 libxext6 curl wget …...
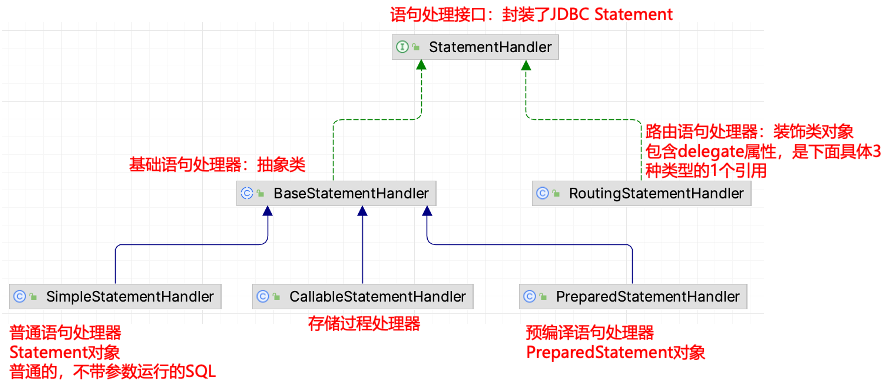
从仿写持久层框架到MyBatis核心源码阅读
接上篇手写持久层框架:https://blog.csdn.net/liwenyang1992/article/details/134884703 MyBatis源码 MyBatis架构原理&主要组件 MyBatis架构设计 MyBatis架构四层作用是什么呢? API接口层:提供API,增加、删除、修改、查询…...

浏览器常用基本操作之python3+selenium4自动化测试
1、打开指定的网页地址 我们使用selenium进行自动化测试时,打开浏览器之后,第一步就是让浏览器访问我们指定的地址,可使用get方法实现 1 2 3 from selenium import webdriver driver webdriver.Edge() driver.get(https://www.baidu.com/)…...

在MySQL中使用VARCHAR字段进行日期筛选
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

微信小程序自定义步骤条效果
微信小程序自定义一个步骤条组件,自定义文字在下面,已完成和未完成和当前进度都不一样的样式,可点击上一步和下一步切换流程状态,效果如下。 这是视频效果: 前端实现步骤条效果 下面我们一步步实现编码,自定…...

QT的信号与槽
QT的信号与槽 文章目录 QT的信号与槽前言一、QT 打印"hello QT"的dome二、信号和槽机制?二、信号与槽的用法1、QT5的方式1. 无参的信号与槽的dome2.带参的信号与槽dome 2、QT4的方式3、C11的语法 Lambda表达式1、函数对象参数2、操作符重载函数参数3、可修…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
