软件测试/测试开发丨Python 模块与包
python 模块与包
python 模块
项目目录结构
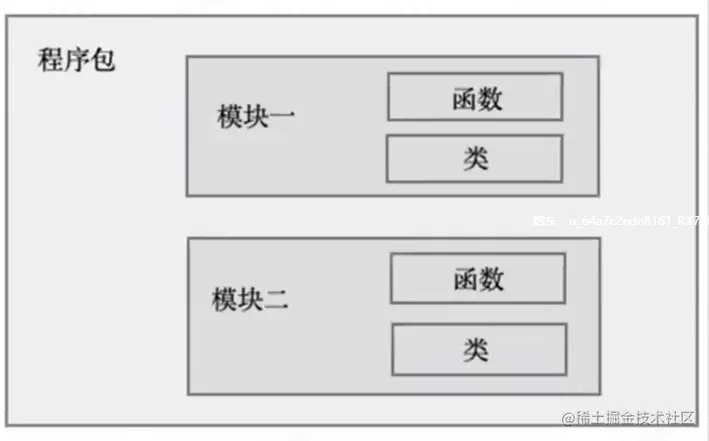
- 组成
- package包
- module模块
- function方法
模块定义
定义
- 包含python定义和语句的文件
- .py文件
- 作为脚本运行
导入模块
- import 模块名
- from <模块名> import <方法 | 变量 | 类>
- from <模块名> import *
- 注意:
- 同一个模块写多次,只被导入一次
- import 应该放在代码的顶端
模块的分类
- 系统内置模块
- 第三方的开源模块
- 自定义模块
文件引用
- 系统内置模块
** python安装好之后自带的一些非常有用的模块(sys,os,time,json模块等) - 第三方开源模块
** 是通过包管理工具pip完成的 - 自定义模块
** 自定义模块是自己写的模块,对某段逻辑或某些函数进行封装后供其他函数调用
# 系统内置模块
import sys
import os
import re # 正则
import json # json文件处理
import time # 时间
print(sys.path)
# 第三方模块
import yaml # 命令行可以命令安装 pip install pyyaml
import requests # 命令行可以命令安装 pip install requests
# 自定义模块
from test import *
print(dir())
模块引用的总结
- 代码的可维护性
- 提升编码效率
- 函数名可重复(起名避免与系统重复)
最后感谢每一个认真阅读我文章的人,礼尚往来总是要有的,虽然不是什么很值钱的东西,如果你用得到的话可以直接拿走:
这些资料,对于【软件测试】的朋友来说应该是最全面最完整的备战仓库,这个仓库也陪伴上万个测试工程师们走过最艰难的路程,希望也能帮助到你!

相关文章:

软件测试/测试开发丨Python 模块与包
python 模块与包 python 模块 项目目录结构 组成 package包module模块function方法 模块定义 定义 包含python定义和语句的文件.py文件作为脚本运行 导入模块 import 模块名from <模块名> import <方法 | 变量 | 类>from <模块名> import * 注意&a…...
java企业网站系统Myeclipse开发mysql数据库web结构java编程计算机网页项目
一、源码特点 java Web企业网站系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为 TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0&…...
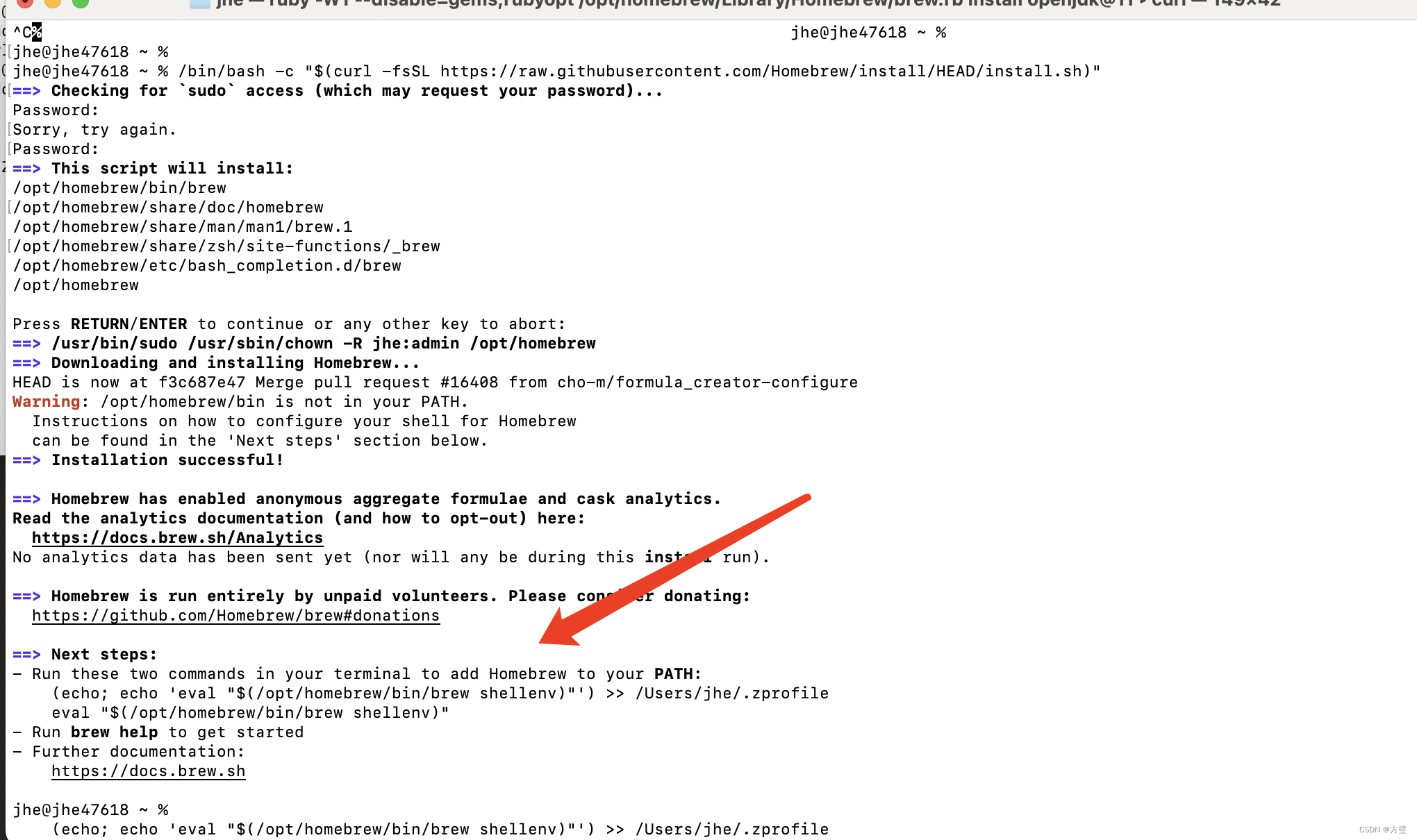
MAC电脑安装java开发工具
一、安装brew 1.1、官网地址 链接 1.2、更新地址 二、安装 java brew install openjdk11 三、安装gradle Gradle安装与配置教程 - 知乎 四、GIT 4.1、GIT安装 brew install git 4.2、rsa ssh-keygen -t rsa -C "jhestarbucks.com" 五、自动搭建一个springBoot…...
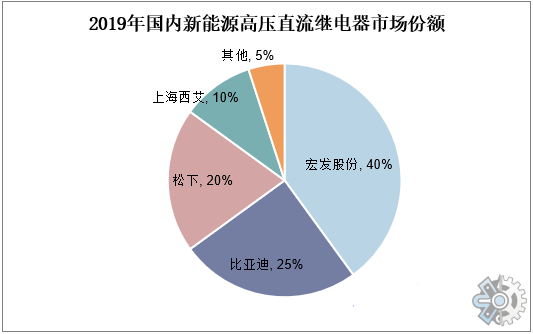
高压继电器,未来几年市场将保持稳定增长
高压继电器是一种用于控制大功率电气设备的开关装置,广泛应用于电力系统、轨道交通、工业自动化等领域。随着各行业对电气控制需求的不断增加,高压继电器市场也在不断扩大。全球高压继电器市场分析: 在全球市场中,目前主要的高压继…...

在Go语言中实现HTTP请求的缓存
大家好,我是你们可爱的编程小助手,今天我们要一起探讨如何使用Go语言实现HTTP请求的缓存。听起来是不是很酷?让我们开始吧! 首先,我们要明白什么是缓存。简单来说,缓存就是将数据存储在内存中,…...

技术扫盲:如何优雅的使用 java -jar
java -jar xxx.jar java -jar 是一个用于在命令行界面中执行 Java 可执行 JAR 文件的命令。它的语法如下: java -jar <JAR 文件路径> [参数]其中: java 是 Java 运行时环境的可执行文件。-jar 是一个选项,表示要执行的文件是一个 JA…...
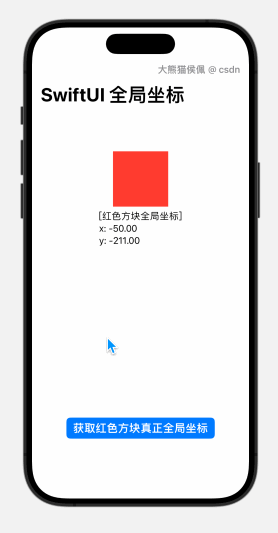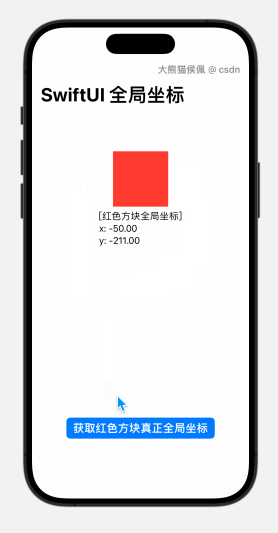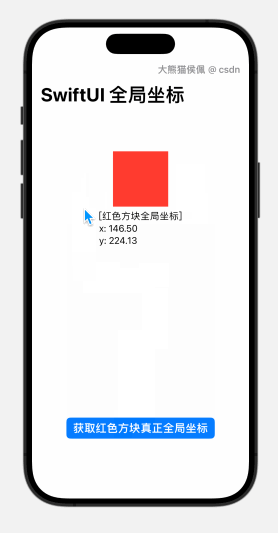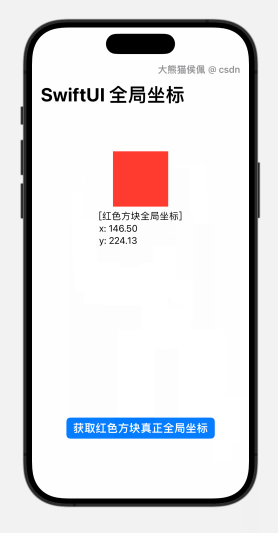
『番外篇七』SwiftUI 获取视图全局位置在 NavigationStack 中失效的解决方法
概览 在 番外篇六』SwiftUI 取得任意视图全局位置的三种方法 这篇博文里,我们详细讨论了在 SwiftUI 中获取任意视图全局坐标的几种方法。 不过,我们也从中提到了某些方法无法适用于 NavigationStack 视图,本篇博文由此应运而生。 在本篇博文种,您将学到如下内容: 概览1.…...
GBASE南大通用 GCDW阿里云计算巢:自动化部署云原生数据仓库
目前,GBASE南大通用已与阿里云计算巢合作,双方融合各自技术优势,助力企业用户实现云上数据仓库的自动化部署,让用户在云端获取数据仓库服务“更简单”,让用户在云端使用数据仓库服务“更便捷”,满足企业用户…...
Docker实战02|Namespace
在上一文《Docker实战01|容器与开发语言》中主要介绍了Docker的基本概念与Docker安装、Go语言安装等实战技巧。 本文继续针对Namespace技术展开讲解并利用Go语言进行实践。 本系列所有代码均已经开源。关公众号回复「Go语言实现Docker」即可获得。 目录 2.1.2 U…...

01-03
利用模板类完成顺序表...

数据可视化与地理空间
写在开头 数据可视化是将数据以图形形式呈现,使其更易于理解和分析的过程。在地理空间分析中,数据可视化不仅能够展示地理位置信息,还能够有效地传达地理空间数据的模式、趋势和关联。本文将探讨数据可视化在地理空间分析中的作用,介绍Python中常用的数据可视化工具,并深…...

【elfboard linux开发板】4. 文件点灯与创建多进程
ps:提升效率的小tips: 灵活运用vim操作命令,gg快速跳转到文件开头,G跳转到结尾 多行操作 ctrl V shift i 插入修改内容 esc退出编辑 sudo vi /etc/vim/vimrc 在文件中添加如下内容省略重复工作: autocmd BufNewFile …...
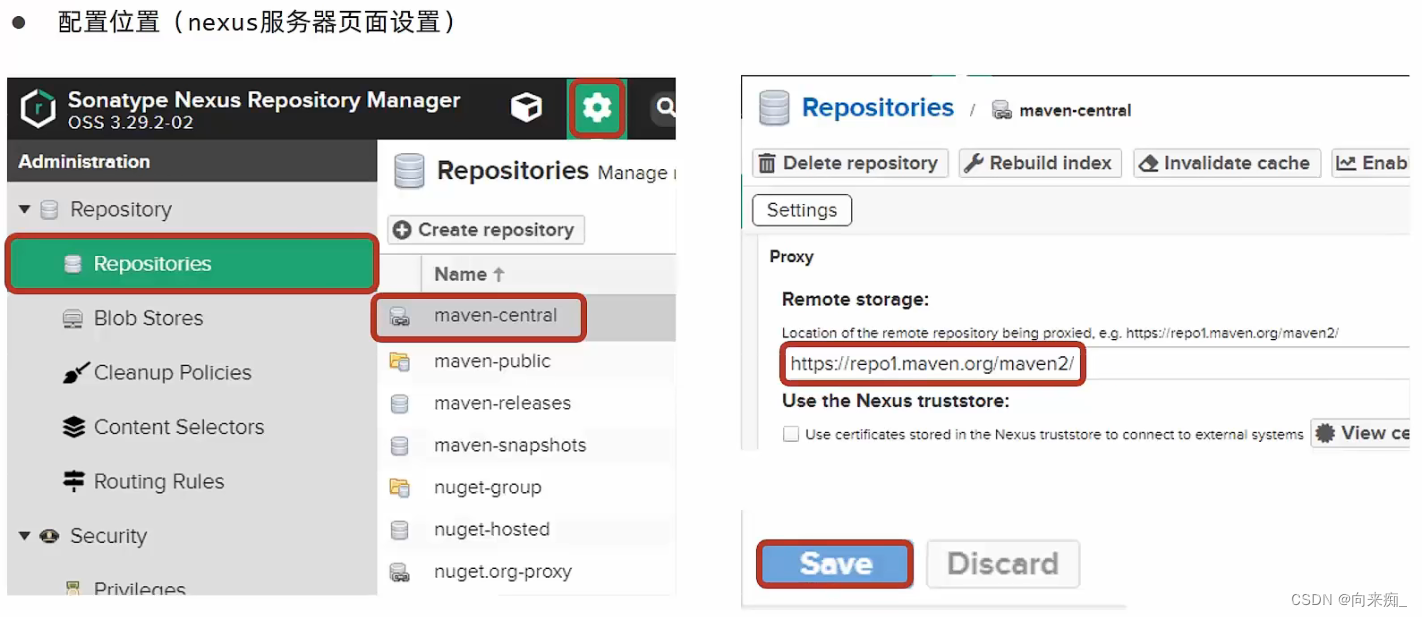
黑马程序员SSM框架-Maven进阶
视频链接:Maven-01-分模块开发的意义_哔哩哔哩_bilibili 分模块开发与设计 分模块开发意义 分模块开发 依赖管理 依赖传递 依赖传递冲突问题 可以点击红框按钮查看依赖情况。 可选依赖和排除依赖 继承和聚合 聚合 聚合工程开发 继承 聚合和继承的区别 属性 属性…...

MFC综合实验二学习记录
文章目录 虚函数和纯虚函数的区别?MFC中什么是UPDATE_COMMAND_UI 消息如何查看控件对应的成员变量模态对话框的理解HGDIOBJ" 类型的值不能用于初始化 "CBrush *" 类型的实体错误MFC编程中CDC类型和HDC类型有什么区别?关于WIDING和ALTERNA…...
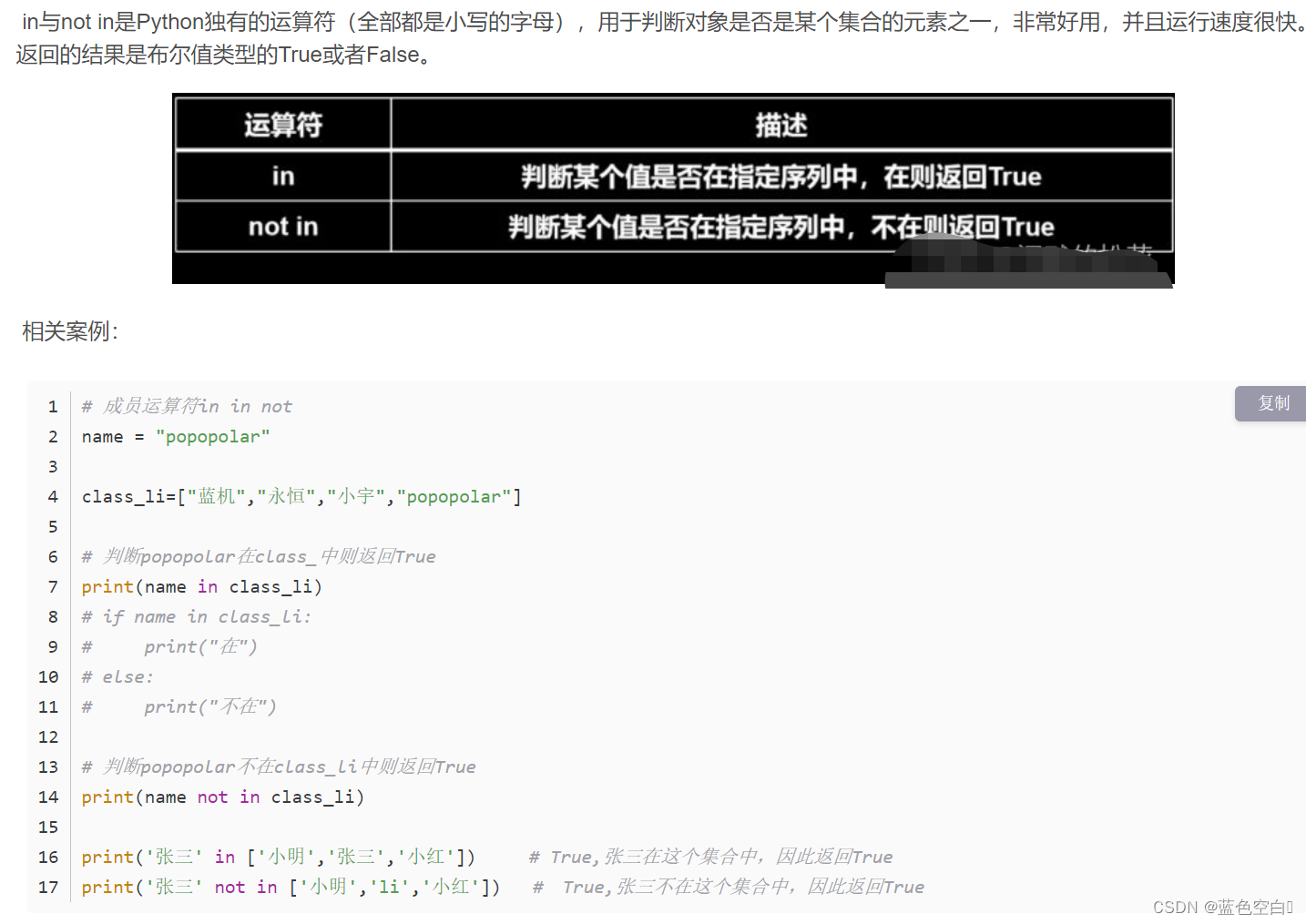
Python 中的运算符介绍(1)
算数运算符 常见的% 、//、/ 用法 赋值运算符 赋值运算:将等号右边赋值给等号左边 常见场景: 比较运算符 代码解析: 逻辑运算符 位运算符(了解) 三目运算符 身份证运算符 成员运算符...
达梦数据库查询各表数据量/以及达梦更新统计信息
1、达梦数据库查询各表数据量 达梦数据库与开源的MySQL不一样,MySQL查询各表数据量非常简单 而达梦数据库就有一些地方要注意,先用这句去查↓ SELECT table_name, num_rows FROM all_tables WHERE tablespace_name 表空间名; 如果结果如下图一样&…...

Java---- 静态内部类与非静态内部类的区别
在面试中回答的很不全,所以再此做一个总结。 1 static 静态修饰符 在程序中任何变量或者代码都是在编译时由系统自动分配内存来存储的。 static修饰表示静态的,在类加载时JVM会把它放到方法区,被本类以及本类中所有实例所公用。在编译后所分…...
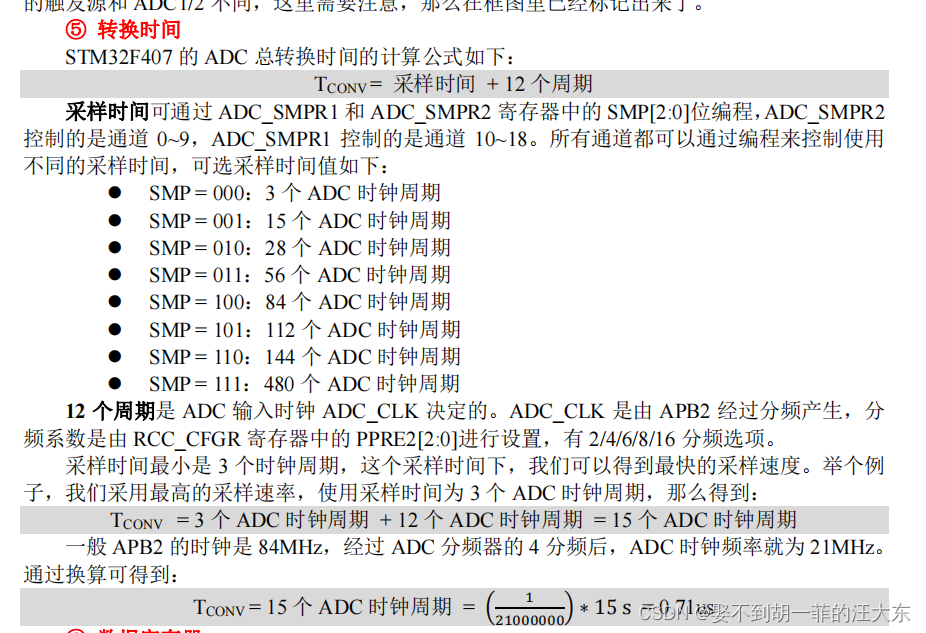
STM32 基础知识(探索者开发板)--135讲 ADC转换
ADC定义: ADC即模拟数字转换器,英文详称 Analog-to-digital converter,可以将外部的模拟信号转换 ADC数模转换中一些常用函数: 1. HAL_ADC_Init 函数 HAL_StatusTypeDef HAL_ADC_Init(ADC_HandleTypeDef *hadc); 初始化ADC 形参&…...

Java经典框架之SpringBoot
SpringBoot Java 是第一大编程语言和开发平台。它有助于企业降低成本、缩短开发周期、推动创新以及改善应用服务。如今全球有数百万开发人员运行着超过 51 亿个 Java 虚拟机,Java 仍是企业和开发人员的首选开发平台。 课程内容的介绍 1. SpringBoot基础 2. Spring…...

LeetCode75| 二叉搜索树
目录 700 二叉搜索树中的搜索 迭代 递归 450 删除二叉搜索树中的节点 700 二叉搜索树中的搜索 注意二叉搜索树的性质即可 迭代 class Solution { public:TreeNode* searchBST(TreeNode* root, int val) {while(root ! NULL){if(root->val < val)root root->r…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...


