Scikit-Learn线性回归(四)
Scikit-Learn线性回归四:梯度下降
- 1、梯度下降
- 1.1、梯度下降概述
- 1.2、梯度下降及原理
- 1.3、梯度下降的实现
- 2、梯度下降法求解线性回归的最优解
- 2.1、梯度下降法求解的原理
- 2.2、梯度下降法求解线性回归的最优解
- 2.3、梯度下降法求解线性回归案例(波士顿房价预测)
- 3、Scikit-Learn梯度下降法
- 3.1、随机梯度下降
- 3.2、Scikit-Learn梯度下降法API
- 3.3、Scikit-Learn梯度下降法案例(波士顿房价预测)
1、梯度下降
1.1、梯度下降概述
在第一篇文章 Scikit-Learn线性回归(一) 中,我们给出了线性回归的损失函数的定义:
L = ∑ i = 1 m ( y i − f ( x i ) ) 2 L=\sum_{i=1}^m(y_i-f(x_i))^2 L=i=1∑m(yi−f(xi))2
回忆一下,损失函数主要用于评估模型拟合的好坏,损失函数衡量了我们构造的模型的预测值与真实值的差异,因此,我们希望我们的预测结果与真实值的差异越小越好。也就是我们希望损失函数取得最小值
损失函数取得最小值是我们构建模型的本质要求,求解模型的特征向量 ω \omega ω是我们构建模型的核心问题
根据损失函数(最小二乘法),我们的求解目标可以转换为求解误差平方和(残差平方和)的最小值:
m i n ω = ∣ ∣ Y − X ω ∣ ∣ 2 2 min_\omega={||Y-X\omega||_2}^2 minω=∣∣Y−Xω∣∣22
而根据数学知识,当我们的误差平方和取得最小值时,线性回归模型特征 ω \omega ω就是最优解
最优解的求解方法主要有两种:最小二乘法(数学方式)和梯度下降法。最小二乘法通过数学求导的方式求函数的极值进而推导出线性回归的解;而梯度下降采用近似逼近,是一种迭代方法
在线性回归(详见:传送门)一文中,我们已经通过最小二乘法推导了线性回归的解析解的正规方程:
ω = ( X T X ) − 1 X T Y \omega=(X^TX)^{-1}X^TY ω=(XTX)−1XTY
然而,很多模型通过这种数学方式求解是推导不出解析解的,所以就需要使用梯度下降法来搜索最优解。基于梯度下降我们可以推导出线性回归的最优解析解。梯度下降法是使用最广泛的一种优化方法
梯度下降法不是机器学习专属的算法,它是一种基于搜索的优化方法,也就是通过不断的搜索然后找到损失函数的最小值
1.2、梯度下降及原理
观察我们的损失函数转换后的求解目标,根据数学知识,误差平方和(函数)为二次函数形式,且函数开口向上,因此,函数一定有唯一最小值。当函数取得最小值时的 ω \omega ω就是最优解

上图中,纵坐标表示损失函数L的值,横坐标表示系数 ω \omega ω,每一个 ω \omega ω都会对应一个损失函数L的值,我们希望损失函数收敛,即找到一个 ω \omega ω值,使得损失函数L的值最小
根据数学知识,要判断一个点A是否是损失函数L的最小值,即求该点的导数。点A的导数就是该点切线的斜率,所以导数描述了一个函数在某一点附近的变化率,并且导数大于零时,函数在区间内单调递增,导数小于零时函数在区间内单调递减
所以, ∂ L ∂ ω \frac{\partial L}{\partial\omega} ∂ω∂L表示损失函数L增大的变化率,- ∂ L ∂ ω \frac{\partial L}{\partial\omega} ∂ω∂L表示损失函数L减小的变化率
再在曲线上定义一点B,B点的 ω \omega ω就是A点的 ω \omega ω值加上损失函数L递减变化率- η ∂ L ∂ ω \eta\frac{\partial L}{\partial\omega} η∂ω∂L:
ω B = ω A − η ∂ L ∂ ω = ω A + ∇ J (
相关文章:

Scikit-Learn线性回归(四)
Scikit-Learn线性回归四:梯度下降 1、梯度下降1.1、梯度下降概述1.2、梯度下降及原理1.3、梯度下降的实现2、梯度下降法求解线性回归的最优解2.1、梯度下降法求解的原理2.2、梯度下降法求解线性回归的最优解2.3、梯度下降法求解线性回归案例(波士顿房价预测)3、Scikit-Learn…...
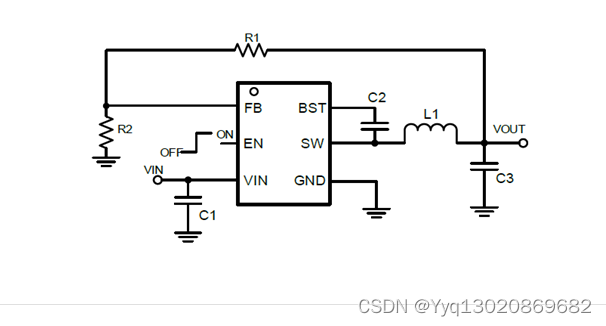
SCT2330C——3.8V-28V输入,3A,低EMI,超低功耗同步降压DCDC转换器
描述: SCT2330C是3A同步buck变换器,输入电压范围高达28V,完全集成了80mΩ高压侧MOSFET和42mΩ低压侧MOSFET,提供高效降压DC-DC转换。SCT2330C采用峰值电流模式控制,集成补偿网络,通过最小化片外元件数量&a…...

php生成唯一ID的5种方法介绍
php生成唯一ID的5种方法介绍 工作中使用到唯一ID的场景非常多,如临时缓存文件、临时变量、临时安全码等。 uniqid()函数基于以微妙计的当前时间,生成一个唯一的ID。由于生成唯一ID与微妙时间关联,因此生成ID的唯一性非常可靠。 生成的唯一…...
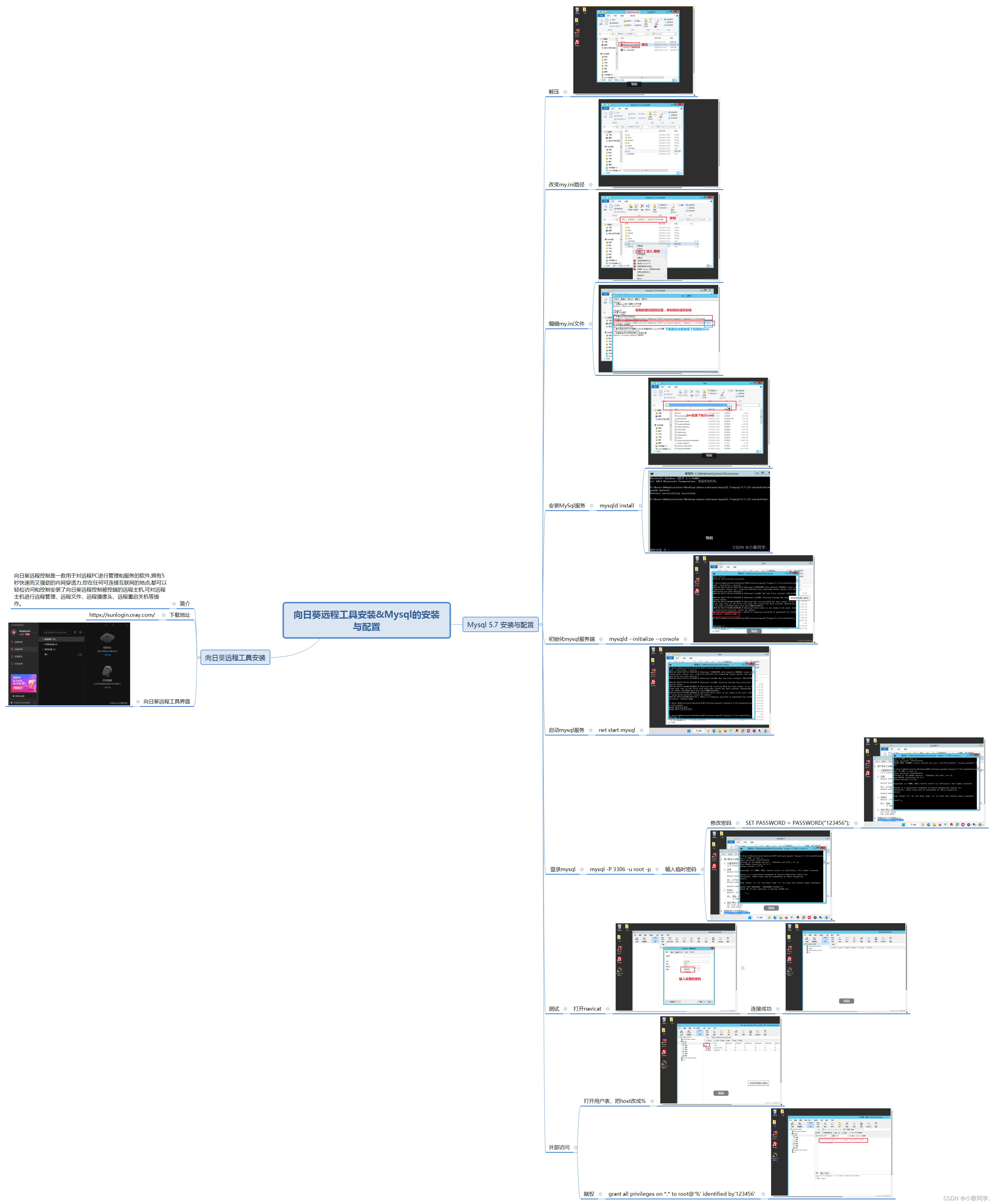
向日葵远程工具安装Mysql的安装与配置
目录 一、向日葵远程工具安装 1.1 简介 1.2 下载地址 二、Mysql 5.7 安装与配置 2.1 简介 2.2 安装 2.3 初始化mysql服务端 2.4 启动mysql服务 2.5 登录mysql 2.6 修改密码 2.7 设置外部访问 三、思维导图 一、向日葵远程工具安装 1.1 简介 向日葵远程控制是一款用…...
Unity 欧盟UMP用户隐私协议Android接入指南
Unity 欧盟UMP用户协议Android接入指南 官方文档链接开始接入mainTemplate.gradle 中引入CustomUnityPlayerActivity 导入UMP相关的包java类中新增字段初始化UMPSDK方法调用测…...

AutoLisp入门教程
AutoLisp入门教程 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!在编程的世界里,有许多领域和语言需要我们去探索,今天我们将聚焦于 AutoLI…...
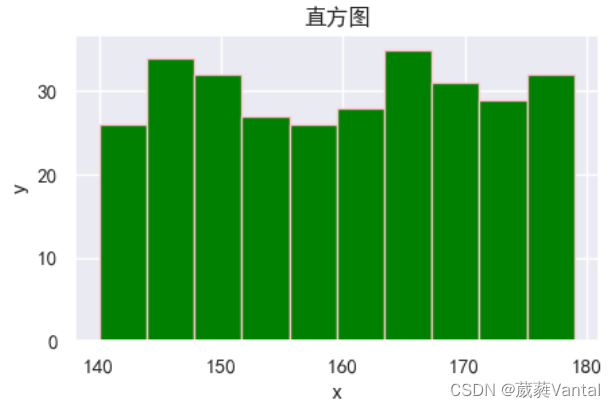
matplotlib颜色合集——各种常见简单图形(上)
一、.颜色配图表 图文颜色引用:建站教程 - FINTHON 二、折线图 jupyter notebook 简介plot() 2.1折线图参数 plt.plot(*args, scalexTrue, scaleyTrue, dataNone, **kwargs) 2.2、参数介绍 x:X轴数据,列表或数组,可选。 y&a…...
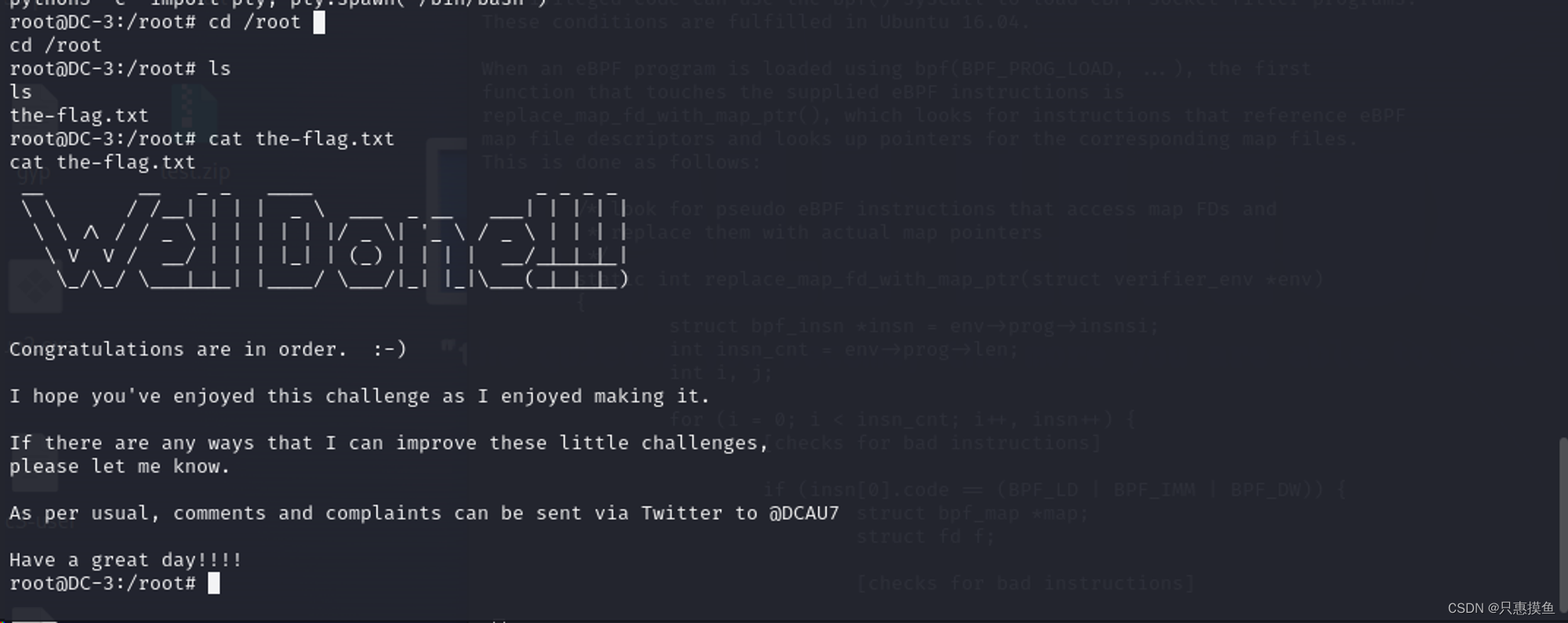
小H靶场笔记:DC-3
DC-3 January 3, 2024 4:11 PM Tags:Joomla owner:只惠摸鱼 信息收集 探测靶机ip: 192.168.199.133 nmap 扫描端口、 系统版本 漏洞 发现只有80端口开发, 且有cve-2017-8917漏洞存在是Joomla的SQL注入漏洞 Joomla版本为3.7.0…...

Web网页开发-CSS高级技巧2-笔记
1.已知宽高垂直水平居中 定位负margin法: 利用top:50%;left:50%;margin-left:子盒子宽度的一半;margin-top:子盒子高度的一半; 2.不定宽高垂直水平居中 兼容性最好的方案: 用定位margin:auto,定位 四个方向的值相等margin:auto…...

C++面向对象语法总结(二)
目录 《C基础语法总结》《C面向对象语法总结(一)》 十一、继承 继承,可以让子类拥有父类的多有成员(变量、函数)如下面的代码:Student是子类(subclass,派生类),Person是父类&…...

【LeetCode每日一题】2487. 从链表中移除节点(调用栈+递归+翻转链表)
2024-1-3 文章目录 [2487. 从链表中移除节点](https://leetcode.cn/problems/remove-nodes-from-linked-list/)方法一:调用栈方法二:递归方法三:翻转链表 2487. 从链表中移除节点 方法一:调用栈 1.将所有节点按顺序压入栈中 2.从…...

开源协助平台工程灵活应对多云时代的挑战
平台工程通过标准化控制和灵活性保障了开发实践。但是,随着平台工程的兴起,开源战略又该如何融入其中呢? 虽然平台工程没有一刀切的方法,但越来越明显的是,开源软件和技术对平台工程的成功绝对至关重要——这一点我将在…...
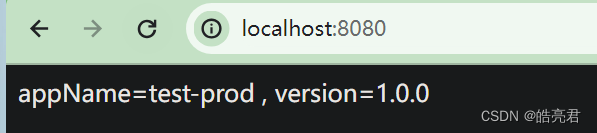
Springboot通过profiles切换不同环境使用的配置
文章目录 简介1.通过分隔符隔离2.通过使用不同的配置文件区分3.测试 简介 一个项目从开发到上线一般要经过几个环境, dev测试环境-uat预生产环境-prod生产环境,每个环境的使用的数据库或者配置不同,这时候可以通过下面两种方式区分配置,达到快速切换的效…...

SpringBoot入门到精通-Spring Boot Jasypt Encrypt 演示
这是 spring boot 应用程序,展示了如何使用 Jasypt 加密值。 关于Jasypt Jasypt 为您提供简单的单向(摘要)和双向加密技术。开放 API,可与任何 JCE 提供程序一起使用,而不仅仅是默认的 Java VM 提供程序。Jasypt 可以很容易地与 Bouncy Castle 等知名提供商一起使用。了解…...
是所有小于及等于)
整数的阶乘(英语:factorial)是所有小于及等于
整数的阶乘(英语:factorial)是所有小于及等于该数的正整数的积,0的阶乘为1。即:n!123...n。 实例 #!/usr/bin/python3 # Filename : test.py # author by : www.dida100.com # 通过用户输入数字计算阶乘 # 获…...

音视频通信
文章目录 一、音视频通信流程二、流媒体协议1、RTSP2、RTMP3、HLS4、WebRTC 一、音视频通信流程 音视频通信完整流程有如下几个环节:采集、编码、前后处理、传输、解码、缓冲、渲染等。 每一个细分环节,还有更细分的技术模块。比如,前后处…...
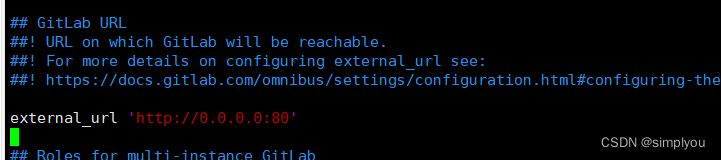
docker 搭建gitlab 恢复和备份
最近一直在折腾gitlab 代码管理系统 采用docker搭建 镜像网址 https://hub.docker.com/ 技术交流 http://idea.coderyj.com/ 1.因为我要恢复的版本是12.0.9的所有我就下载了docker-ce的12.0.9的镜像 1.下载镜像 docker pull gitlab/gitlab-ce:12.0.9-ce.02.安装 docker run …...
)
尚硅谷2023版Promise教程从入门到实战(讲师:任安萍)
一、前言:为什么会出现Promise? Promise的重要性我认为没有必要多讲,概括起来说就是五个字:必!须!得!掌!握!。 而且还要掌握透彻,在实际的使用中,有非常多…...

【SpringBoot】分组校验和自定义校验
分组检验 参数校验时,我们希望不同的方法参数校验规则不同,这时就需要分组校验。 public class Category {NotNull(groups Update.class)private Integer id;//主键IDNotEmptyprivate String categoryName;//分类名称// NotEmpty(groups {Add.class,…...
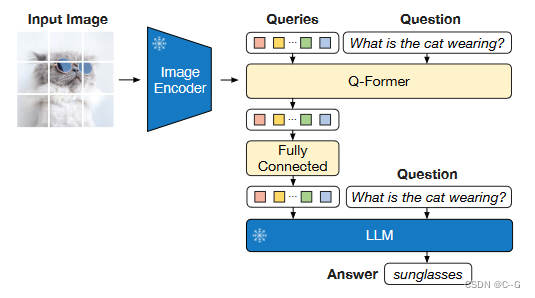
19、BLIP-2
简介 github 通过利用预训练的视觉模型和语言模型来提升多模态效果和降低训练成本,预训练的视觉模型能够提供高质量的视觉表征,预训练的语言模型则提供了强大的语言生成能力。 实现过程 为了弥合模态差距,提出了一个分两个阶段预训练的 Qu…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...
