Linux C/C++ 获取CPUID
实现方式:
INTEL CC 格式
AT^T CC 格式
GCC/C库 __cpuid 宏
大致讲义:
AT^T 格式汇编很反人类,GCC可以改编译器选项为INTEL内嵌汇编,但一般在GCC还是按照默认的AT^T汇编来拽写把,不想用也可以让AI工具把INTEL内嵌汇编转换为AT^T汇编(让 bard、gpt、bing 干这种反人类的活很好用),AT^T汇编格式没有学的必要,这是一个反人类的东西。
__asm__ __volatile__(
"movl $0x00, %%eax\n\t"
"xorl %%edx, %%edx\n\t"
"cpuid\n\t"
"movl %%eax, %0\n\t"
"movl %%edx, %1\n\t"
: "=m" (s1), "=m" (s2)
:
: "%eax", "%edx"
);
汇编是一种面向地址标识符及通用寄存器编程的低级语言。
IL: 把立即数0移动到EAX寄存器,CPU参数(LEVEL,CPU内置指令函数取值范围0~1)
IL: 把EDX寄存器XOR(亦或)重置为0
IL: cpuid 指令(会推送值到EAX、EBX、ECX、EDX 四个寄存器之中,SN[4])
IL: 把EAX寄存器的值复制给内链参数一(注意是压入是内存地址,%0 = s1变量)
IL: 把EDX寄存器的值复制给内链参数二(注意是压入是内存地址,%1 = s2变量)
声明内嵌所需要的寄存器与变量内存地址。
注解:
__asm__ __volatile__ ("movl $0x00, %%eax\n\t" // 将立即数 0x00 移动到 eax 寄存器中"xorl %%edx, %%edx\n\t" // 将 edx 寄存器与自身进行异或操作,相当于将 edx 清零"cpuid\n\t" // 执行 cpuid 指令,用于获取 CPU 的信息"movl %%eax, %0\n\t" // 将 eax 寄存器的值移动到 s1 变量中"movl %%edx, %1\n\t" // 将 edx 寄存器的值移动到 s2 变量中: "=m" (s1), "=m" (s2) // 输出操作数列表,将 s1 和 s2 分别与 %0 和 %1 关联起来: // 输入操作数列表为空: "%eax", "%edx" // 使用了 eax 和 edx 寄存器,需要在此处进行声明
);具体实现:
#if defined(__x86_64__) || defined(_M_X64) || defined(i386) || defined(__i386__) || defined(__i386) || defined(_M_IX86)ppp::string CPUID() noexcept { int s1, s2, s3, s4;// int sn[4]; /* #include <cpuid.h> */// __cpuid(0, sn[0], sn[1], sn[2], sn[3]);// s1 = sn[0];// s2 = sn[3];// __cpuid(1, sn[0], sn[1], sn[2], sn[3]);// s3 = sn[0];// s4 = sn[3];// INTEL CC:// __asm // {// mov eax, 00h// xor edx, edx// cpuid// mov dword ptr[s1], eax// mov dword ptr[s2], edx// }// __asm // {// mov eax, 01h// xor ecx, ecx// xor edx, edx// cpuid// mov dword ptr[s3], eax// mov dword ptr[s4], edx// }// AT&T CC__asm__ __volatile__("movl $0x00, %%eax\n\t""xorl %%edx, %%edx\n\t""cpuid\n\t""movl %%eax, %0\n\t""movl %%edx, %1\n\t": "=m" (s1), "=m" (s2):: "%eax", "%edx");__asm__ __volatile__("movl $0x01, %%eax\n\t""xorl %%ecx, %%ecx\n\t""xorl %%edx, %%edx\n\t""cpuid\n\t""movl %%eax, %0\n\t""movl %%edx, %1\n\t": "=m" (s3), "=m" (s4):: "%eax", "%ecx", "%edx");// You can query all CPU processor instances using WQL in wbemtest, // View the ProcessorId attribute of the processor instance MOF, // And clarify the rules for the operating system CPUID to obtain and format as text.char buf[40];snprintf(buf, sizeof(buf), "%016llX %016llX",(long long unsigned int)((int64_t)s4 << 32 | (int64_t)s3),(long long unsigned int)((int64_t)s2 << 32 | (int64_t)s1));return buf;}
#endif相关文章:

Linux C/C++ 获取CPUID
实现方式: INTEL CC 格式 AT^T CC 格式 GCC/C库 __cpuid 宏 大致讲义: AT^T 格式汇编很反人类,GCC可以改编译器选项为INTEL内嵌汇编,但一般在GCC还是按照默认的AT^T汇编来拽写把,不想用也可以让AI工具把INTEL内嵌…...
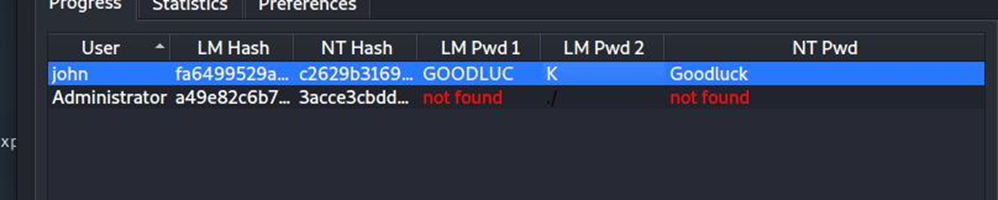
2023年“中银杯”安徽省网络安全B模块(部分解析)
前言 以下是2023年中银杯安徽省网络安全B模块题目,镜像可以私聊我 B模块安全事件响应/网络安全数据取证/应用安全(400 分) B-1:CMS网站渗透测试 任务环境说明: √服务器场景:Server2206(关…...
】单行道汽车通行时间(迭代计算—JavaPythonC++JS实现))
194.【2023年华为OD机试真题(C卷)】单行道汽车通行时间(迭代计算—JavaPythonC++JS实现)
请到本专栏顶置查阅最新的华为OD机试宝典 点击跳转到本专栏-算法之翼:华为OD机试 🚀你的旅程将在这里启航!本专栏所有题目均包含优质解题思路,高质量解题代码,详细代码讲解,助你深入学习,深度掌握! 文章目录 【2023年华为OD机试真题(C卷)】单行道汽车通行时间(…...
第二证券机构策略:股指预计维持蓄势震荡格局 关注煤炭、电力等板块
第二证券以为,技能面看,在元旦节前资金抄底推进指数收回2900整数关口,并向着3000点渠道压力前进。沪指在底部均线位支撑摆放较强,调整空间估计不大,在3000点渠道下方调整就是再次优化低吸的时机。操作上,在…...
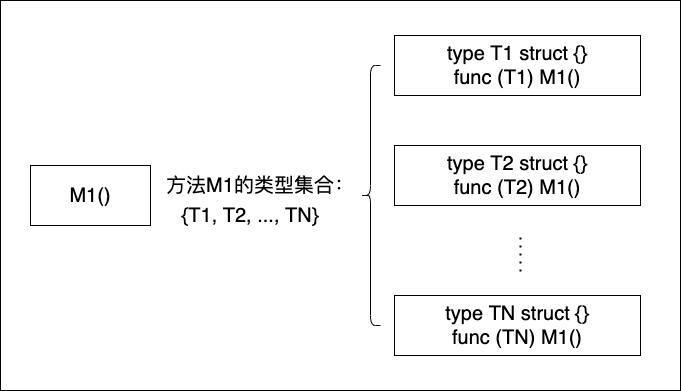
Go 泛型之泛型约束
Go 泛型之泛型约束 文章目录 Go 泛型之泛型约束一、引入二、最宽松的约束:any三、支持比较操作的内置约束:comparable四、自定义约束五、类型集合(type set)六、简化版的约束形式七、约束的类型推断八、小结 一、引入 虽然泛型是…...

【数据仓库与联机分析处理】数据仓库
目录 一、数据仓库的概念 二、数据仓库与操作性数据库的区别 三、发展前期 四、数据仓库的系统结构 五、建模划分 六、主要案例 一、数据仓库的概念 目前很难给数据仓库(Data Warehouse)一个严格的定义,不准确地说,数据仓库…...

机器学习:贝叶斯估计在新闻分类任务中的应用
文章摘要 随着互联网的普及和发展,大量的新闻信息涌入我们的生活。然而,这些新闻信息的质量参差不齐,有些甚至包含虚假或误导性的内容。因此,对新闻进行有效的分类和筛选,以便用户能够快速获取真实、有价值的信息&…...

[C#]基于deskew算法实现图像文本倾斜校正
【算法介绍】 让我们开始讨论Deskeweing算法的一般概念。我们的主要目标是将旋转的图像分成文本块,并确定它们的角度。为了让您详细了解我将使用的方法: 照常-将图像转换为灰度。应用轻微的模糊以减少图像中的噪点。现在,我们的目标是找到带…...

Qt通过pos()获取坐标信息
背景:这是一个QWidget窗体,里面是各种布局的组合,一层套一层。 我希望得到绿色部分的坐标信息(x,y) QPoint get_pos(QWidget* w, QWidget* parent) {if ((QWidget*)w->parent() parent) {return w->pos();}else {QPoint pos(w->po…...

【Webpack】资源输入输出 - 配置资源出口
所有与出口相关的配置都集中在 output对象里 output对象里可以包含数十个配置项,这里介绍几个常用的 filename 顾名思义,filename的作用是控制输出资源的文件名,其形式为字符串,如: module.exports {entry: ./src/a…...

【XR806开发板试用】XR806串口驱动CM32M对小厨宝的控制实验
一.说明 非常感谢基于安谋科技STAR-MC1的全志XR806 Wi-FiBLE开源鸿蒙开发板试用活动,并获得开发板试用。 XR806是全志科技旗下子公司广州芯之联研发设计的一款支持WiFi和BLE的高集成度无线MCU芯片,支持OpenHarmony minisystem和FreeRTOS,具有集成度高、…...

中介者模式-Mediator Pattern-1
如果在一个系统中对象之间的联系呈现为网状结构, 对象之间存在大量的多对多联系,将导致系统非常复杂。 这些对象既会影响别的对象,也会被别的对象所影响。 这些对象称为同事对象,它们之间通过彼此的相互作用实现系统的行为。 在网…...

ASP.NET Core基础之图片文件(一)-WebApi图片文件上传到文件夹
阅读本文你的收获: 了解WebApi项目保存上传图片的三种方式学习在WebApi项目中如何上传图片到指定文件夹中 在ASP.NET Core基础之图片文件(一)-WebApi访问静态图片文章中,学习了如何获取WebApi中的静态图片,本文继续分享如何上传图片。 那么…...

精准掌控 Git 忽略规则:定制化 .gitignore 指南
🧙♂️ 诸位好,吾乃诸葛妙计,编程界之翘楚,代码之大师。算法如流水,逻辑如棋局。 📜 吾之笔记,内含诸般技术之秘诀。吾欲以此笔记,传授编程之道,助汝解技术难题。 &…...

Harmony 开始支持 Flutter ,聊聊 Harmony 和 Flutter 之间的因果
原创作者:恋猫de小郭 相信大家都已经听说过,明年的 Harmony Next 版本将正式剥离 AOSP 支持 ,基于这个话题我已经做过一期问题汇总 ,当时在 现有 App 如何兼容 Harmony Next 问题上提到过: 华为内部也主导适配目前的主…...

k8s 之7大CNI 网络插件
一、介绍 网络架构是Kubernetes中较为复杂、让很多用户头疼的方面之一。Kubernetes网络模型本身对某些特定的网络功能有一定要求,但在实现方面也具有一定的灵活性。因此,业界已有不少不同的网络方案,来满足特定的环境和要求。 CNI意为容器网络…...

stable diffusion 人物高级提示词(一)头部篇
一、女生发型 prompt描述推荐用法Long hair长发一定不要和 high ponytail 一同使用Short hair短发-Curly hair卷发-Straight hair直发-Ponytail马尾high ponytail 高马尾,一定不要和 long hair一起使用,会冲突Pigtails2条辫子-Braid辫子只写braid也会生…...

限制哪些IP能连接postgre
打开C:\Program Files\PostgreSQL\9.4\data\pg_hba.conf 以下代表本机能连,172.16.73.xx都能连(/24就代表最后一位是0-255),如果是172.16.73.11/32那就是限制了172.16.73.11才能连(实际我设置/32是无效的)&…...

可狱可囚的爬虫系列课程 08:新闻数据爬取实战
前言 本篇文章中我带大家针对前面所学 Requests 和 BeautifulSoup4 进行一个实操检验。 相信大家平时或多或少都有看新闻的习惯,那么我们今天所要爬取的网站便是新闻类型的:中国新闻网,我们先来使用爬虫爬取一些具有明显规则或规律的信息&am…...

mysql2pgsql
使用pgloader进行迁移 pgloader是一个强大的数据迁移工具,专为将不同数据库之间的数据迁移到PostgreSQL而设计。它支持从MySQL到PostgreSQL的迁移,并提供了一种简单且灵活的方式来转移数据。 安装pgloader 使用pgloader迁移数据 1、命令行方式 2、脚…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
