降维算法的简单介绍
降维算法
降维算法: 通过减少数据的维度,如主成分分析和 t-分布邻域嵌入等。
降维通俗的讲,是通过减少数据的维度来处理高维数据的过程。降维算法有助于消除数据中的冗余信息,减少噪声,并提高计算效率。以下是一些常见的降维算法:
1.主成分分析(Principal Component Analysis,PCA):原理: 将数据投影到一个新的坐标系,使得数据在新坐标系中的方差最大。特点: 通过选择主成分(新坐标系的基向量)来达到降维的效果,适用于线性数据。算法流程图:标准化数据: 对原始数据进行标准化,使每个特征的均值为0,方差为1。计算协方差矩阵: 计算标准化后的数据的协方差矩阵。计算特征值和特征向量: 对协方差矩阵进行特征值分解,得到特征值和对应的特征向量。选择主成分: 选择最大的k个特征值对应的特征向量,构成投影矩阵。投影: 将标准化后的数据投影到选定的主成分上,得到降维后的数据。
import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt# 生成示例数据
np.random.seed(42)
data = np.random.rand(100, 2) * 10# 使用PCA算法
pca = PCA(n_components=1)
pca_result = pca.fit_transform(data)# 可视化原始数据和主成分
plt.scatter(data[:, 0], data[:, 1], label='Original Data', alpha=0.5)
plt.scatter(pca.components_[0, 0], pca.components_[0, 1], color='red', label='Principal Component', marker='^', s=200)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()
plt.show()2.t-分布邻域嵌入(t-Distributed Stochastic Neighbor Embedding,t-SNE):原理: 将高维空间中的相似性映射到低维空间中,强调保留相似样本之间的距离。特点: 用于可视化高维数据,并保留局部结构,但不适用于全局结构。算法流程图:计算相似度: 对原始高维数据计算相似度矩阵,使用条件概率来表示数据点之间的相似度。定义t分布相似度: 使用t分布的概率分布来定义相似度的分布。随机初始化低维空间: 在低维空间中随机初始化数据点的位置。优化: 通过最小化高维空间和低维空间之间的相似度差异来优化低维空间的布局。这通常使用梯度下降等优化算法来完成。迭代: 重复步骤3和步骤4,直到达到最大迭代次数或达到收敛条件。t-SNE主要用于可视化高维数据,对于大规模数据集,需要谨慎调整参数以避免计算开销过大。在实际应用中,你可能需要进行参数调整以及对结果进行解释和分析。
from sklearn.manifold import TSNE
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt# 加载示例数据集
digits = load_digits()
data = digits.data
target = digits.target# 使用t-SNE算法进行降维
tsne = TSNE(n_components=2, random_state=42)
tsne_result = tsne.fit_transform(data)# 可视化结果
plt.scatter(tsne_result[:, 0], tsne_result[:, 1], c=target, cmap='viridis', marker='o', s=50)
plt.title('t-SNE Visualization')
plt.show()3.多维尺度分析(Multidimensional Scaling,MDS):原理: 将高维数据映射到低维空间,保持样本之间的距离。特点: 适用于保留全局结构,但计算复杂度较高。算法流程图:计算相似度矩阵: 对原始高维数据计算相似度矩阵,通常使用欧氏距离或其他相似性度量。构建距离矩阵: 从相似度矩阵计算距离矩阵,用于表示数据点之间的距离。中心化矩阵: 对距离矩阵进行中心化操作,以确保在低维空间中的数据点之间的内积等于原始距离矩阵中的对应元素。特征值分解: 对中心化的距离矩阵进行特征值分解,得到特征值和对应的特征向量。选择维度: 选择要保留的低维度数量,通常是2或3。映射低维空间: 使用前几个特征向量,将原始高维数据映射到低维空间。
from sklearn.manifold import MDS
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt# 加载示例数据集
digits = load_digits()
data = digits.data
target = digits.target# 使用MDS算法进行降维
mds = MDS(n_components=2, random_state=42)
mds_result = mds.fit_transform(data)# 可视化结果
plt.scatter(mds_result[:, 0], mds_result[:, 1], c=target, cmap='viridis', marker='o', s=50)
plt.title('MDS Visualization')
plt.show()4.自编码器(Autoencoder):原理: 通过神经网络学习数据的紧凑表示,然后将其映射到低维空间。特点: 由编码器和解码器组成,适用于非线性数据降维。算法流程图:构建编码器和解码器: 定义编码器和解码器的结构,通常使用神经网络。定义损失函数: 使用重建误差(如均方差)来定义损失函数,衡量原始输入与重建输出之间的差异。训练自编码器: 通过反向传播算法最小化损失函数,优化编码器和解码器的参数。潜在表示: 使用训练后的编码器将输入数据映射到潜在空间。重建数据: 使用训练后的解码器将潜在表示映射回原始输入空间,重建数据。
from keras.layers import Input, Dense
from keras.models import Model
from keras.datasets import mnist
import matplotlib.pyplot as plt# 加载MNIST数据集
(x_train, _), (x_test, _) = mnist.load_data()# 数据预处理
x_train = x_train.astype('float32') / 255.0
x_test = x_test.astype('float32') / 255.0
x_train = x_train.reshape((len(x_train), -1))
x_test = x_test.reshape((len(x_test), -1))# 构建自编码器模型
input_layer = Input(shape=(784,))
encoded = Dense(128, activation='relu')(input_layer)
decoded = Dense(784, activation='sigmoid')(encoded)autoencoder = Model(input_layer, decoded)
autoencoder.compile(optimizer='adam', loss='mean_squared_error')# 训练自编码器
autoencoder.fit(x_train, x_train, epochs=10, batch_size=256, shuffle=True, validation_data=(x_test, x_test))# 使用训练后的自编码器进行数据重建
decoded_imgs = autoencoder.predict(x_test)# 可视化原始图像与重建图像
n = 10 # 显示的图像数量
plt.figure(figsize=(20, 4))
for i in range(n):# 原始图像ax = plt.subplot(2, n, i + 1)plt.imshow(x_test[i].reshape(28, 28))plt.gray()ax.get_xaxis().set_visible(False)ax.get_yaxis().set_visible(False)# 重建图像ax = plt.subplot(2, n, i + 1 + n)plt.imshow(decoded_imgs[i].reshape(28, 28))plt.gray()ax.get_xaxis().set_visible(False)ax.get_yaxis().set_visible(False)
plt.show()5.因子分析(Factor Analysis):原理: 假设观察到的数据是由一些潜在的因子和噪声共同决定的。特点: 用于识别影响数据变异的潜在因子。算法流程图:设定模型: 确定因子分析模型的结构,包括选择因子数量和确定因子负荷矩阵。拟合模型: 使用最大似然估计或其他方法拟合模型参数,包括因子负荷矩阵和误差方差。获取因子负荷矩阵: 得到因子负荷矩阵,该矩阵描述了观测变量与潜在因子之间的关系。因子得分: 计算每个样本的因子得分,表示潜在因子的影响。解释结果: 分析因子负荷矩阵和因子得分,解释观测变量之间的共享变异性。
from factor_analyzer import FactorAnalyzer
import pandas as pd
import matplotlib.pyplot as plt# 生成示例数据
np.random.seed(42)
data = pd.DataFrame(np.random.rand(100, 5), columns=['Var1', 'Var2', 'Var3', 'Var4', 'Var5'])# 使用因子分析算法
factor_analyzer = FactorAnalyzer(n_factors=2, rotation='varimax')
factor_analyzer.fit(data)# 获取因子负荷矩阵
factor_loadings = factor_analyzer.loadings_# 获取因子得分
factor_scores = factor_analyzer.transform(data)# 可视化因子负荷矩阵
plt.imshow(factor_loadings, cmap='viridis', aspect='auto', interpolation='none')
plt.colorbar()
plt.title('Factor Loadings Matrix')
plt.show()# 打印因子得分
print('Factor Scores:')
print(factor_scores)
6.局部线性嵌入(Locally Linear Embedding,LLE):原理: 在局部对数据进行线性嵌入,保持邻近样本之间的线性关系。特点: 对于流形结构的数据具有良好的效果,但对噪声敏感。算法流程图:选择邻域: 对每个数据点选择其近邻数据点。重构权重: 对每个数据点重构其与邻域数据点之间的线性关系,即通过最小化重构误差找到权重。构建权重矩阵: 将所有数据点的权重组合成权重矩阵。嵌入低维空间: 通过最小化嵌入后的数据点在低维空间中的重构误差,找到最终的低维表示。
from sklearn.datasets import make_swiss_roll
from sklearn.manifold import LocallyLinearEmbedding
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# 生成示例数据集(三维瑞士卷)
data, color = make_swiss_roll(n_samples=1000, random_state=42)# 使用LLE算法进行降维
lle = LocallyLinearEmbedding(n_neighbors=12, n_components=2, method='standard', random_state=42)
lle_result = lle.fit_transform(data)# 可视化结果
fig = plt.figure(figsize=(10, 5))# 原始三维数据可视化
ax1 = fig.add_subplot(121, projection='3d')
ax1.scatter(data[:, 0], data[:, 1], data[:, 2], c=color, cmap='viridis')
ax1.set_title('Original 3D Data')# LLE降维后的二维数据可视化
ax2 = fig.add_subplot(122)
ax2.scatter(lle_result[:, 0], lle_result[:, 1], c=color, cmap='viridis')
ax2.set_title('LLE Embedding (2D)')
plt.show()
7.随机投影(Random Projection):随机投影(Random Projection)是一种用于降维的快速而有效的技术,它通过随机选择投影矩阵来将高维数据映射到低维空间。原理: 通过将数据投影到一个低维的随机子空间来降维。特点: 计算效率高,对于大规模数据集适用。算法流程图:选择投影矩阵: 随机生成或选择一个投影矩阵。投影: 使用选择的投影矩阵将高维数据映射到低维空间。得到降维后的数据: 得到降维后的数据,完成降维过程。
from sklearn.datasets import load_digits
from sklearn.random_projection import GaussianRandomProjection
import matplotlib.pyplot as plt
import numpy as np# 加载示例数据集
digits = load_digits()
data = digits.data
target = digits.target# 使用随机投影算法进行降维
rp = GaussianRandomProjection(n_components=2, random_state=42)
rp_result = rp.fit_transform(data)# 可视化结果
plt.scatter(rp_result[:, 0], rp_result[:, 1], c=target, cmap='viridis', marker='o', s=50)
plt.title('Random Projection')
plt.show()相关文章:

降维算法的简单介绍
降维算法 降维算法: 通过减少数据的维度,如主成分分析和 t-分布邻域嵌入等。 降维通俗的讲,是通过减少数据的维度来处理高维数据的过程。降维算法有助于消除数据中的冗余信息,减少噪声,并提高计算效率。以下是一些常见…...
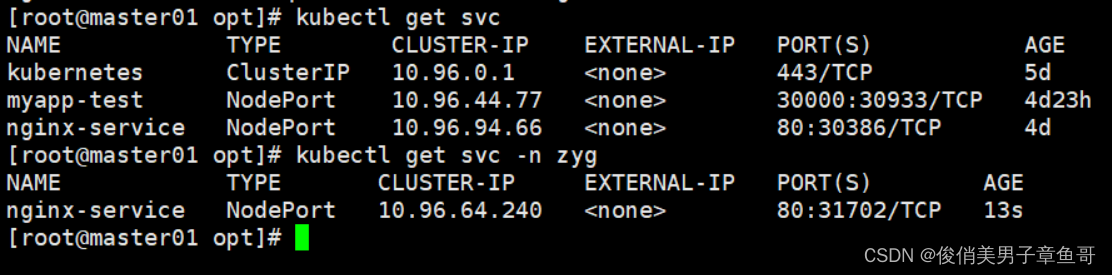
k8s的声明式资源管理
在k8s当中支持两种声明资源的方式: 1、 yaml格式:主要用于和管理资源对象 2、 json格式:主要用于在API接口之间进行消息传递 声明式管理方法(yaml)文件 1、 适合对资源的修改操作 2、 声明式管理依赖于yaml文件,所有的内容都…...

Git | tag相关命令
语法命令 git tag -h usage: git tag [-a | -s | -u <key-id>] [-f] [-m <msg> | -F <file>]<tagname> [<head>]or: git tag -d <tagname>...or: git tag -l [-n[<num>]] [--contains <commit>] [--no-contains <commit&g…...

【Java期末】学生成绩管理系统
诚接计算机专业编程任务(C语言、C、Python、Java、HTML、JavaScript、Vue等)10/15R,如有需要请私信我,或者加我的企鹅号:1404293476 本文资源下载地址:https://download.csdn.net/download/weixin_47040861/88697244 —————…...
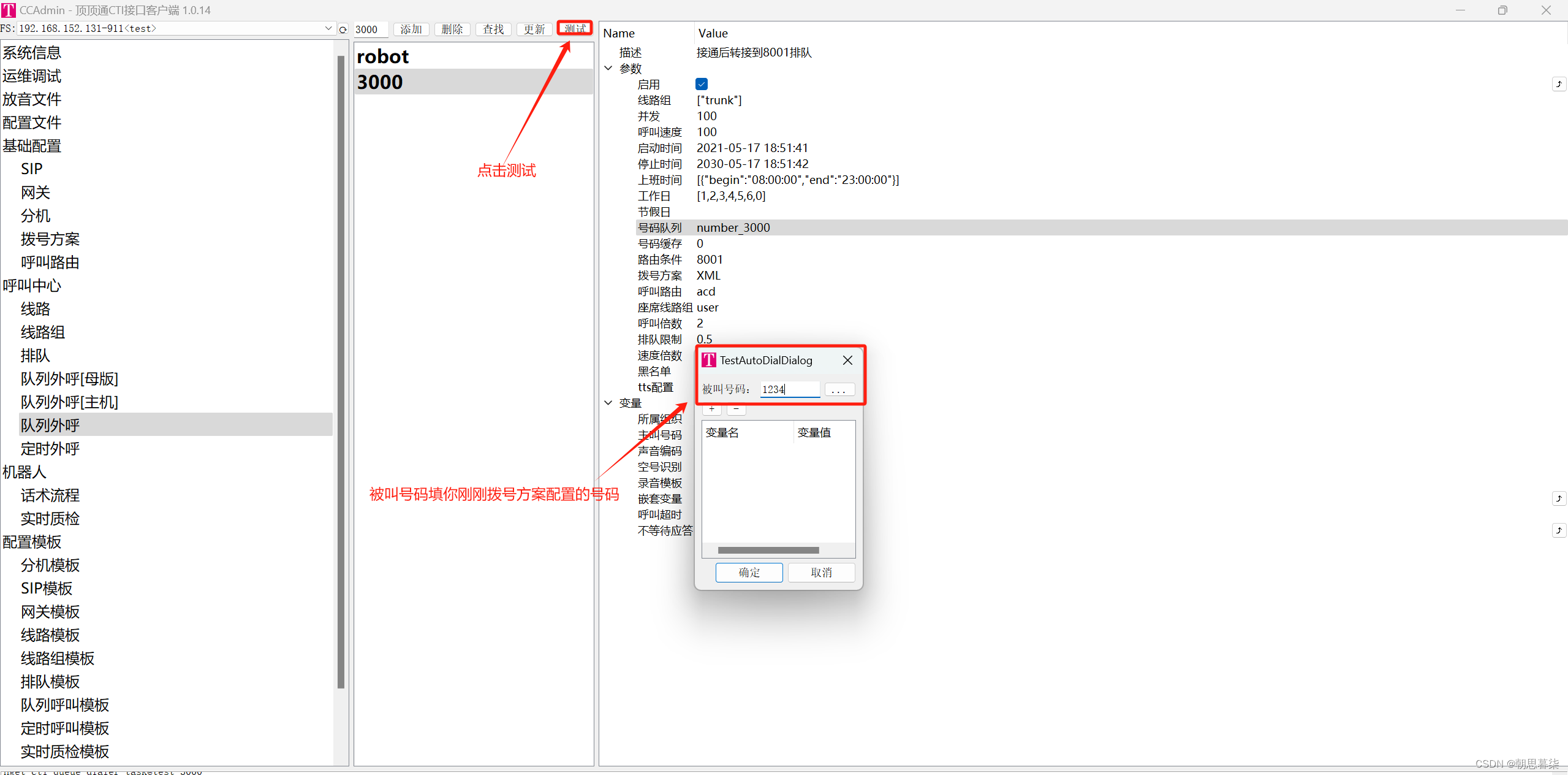
顶顶通呼叫中心中间件通过队列外呼拨打另一个sip并且放音(mod_cti基于FreeSWITCH)
介绍 顶顶通呼叫中心中间件通过队列外呼拨打另一个sip并且放音 一、添加acl 打开ccadmin->点击配置文件->点击acl.conf->在</list>后面添加一条图中的信息->muqi是我自己设置的名字你们可以修改为自己需要的名字->添加好了点击提交XML->在运维调试点…...
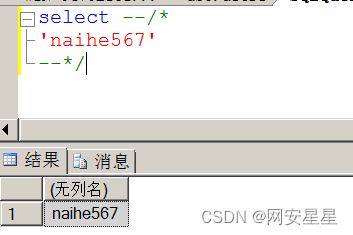
SQL Server从0到1——报错注入
报错注入分为三类:隐式转换,和显示转换,declare函数 隐式转换: 原理:将不同数据类型的数据进行转换或对比 select * from test.dbo.users where (select user)>0 #对比 select * from test.dbo.users where ((sel…...
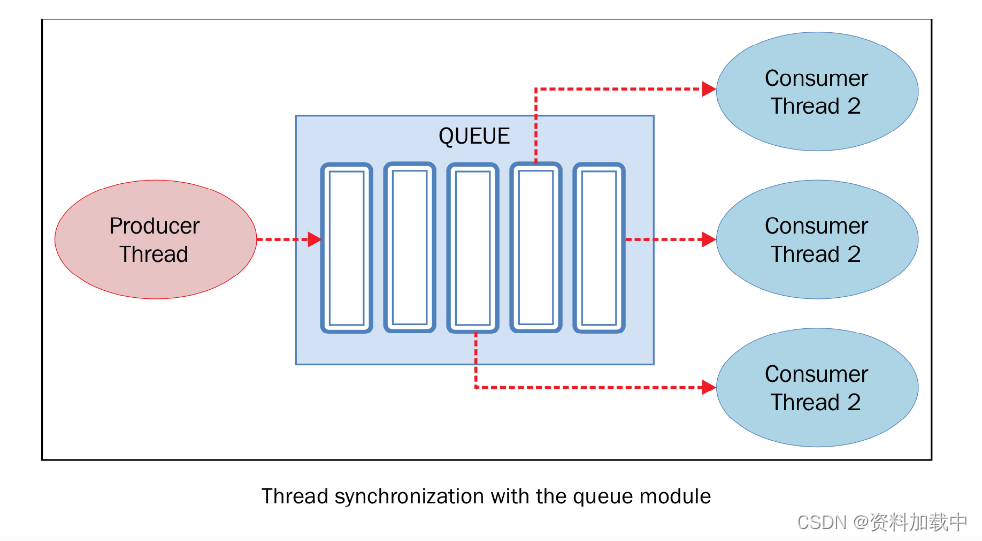
【python高级用法】线程
前言 Python通过标准库的 threading 模块来管理线程。这个模块提供了很多不错的特性,让线程变得无比简单。实际上,线程模块提供了几种同时运行的机制,实现起来非常简单。 线程模块 线程对象Lock对象RLock对象信号对象条件对象事件对象 简单…...

分布式高级知识点
分布式一致性算法: Paxos Paxos 是一种分布式一致性算法,用于在分布式系统中达成共识。它可以保证,即使在存在节点故障的情况下,系统也能就某个值达成一致。 Paxos 算法的基本思想是,首先选出一个协调者(leader)。协调者负责向其他节点发送提案(proposal)。其他节点收…...

Linux 命令之 dpkg 的简单使用
查询已安装的软件包及其依赖关系 dpkg -s name...
Ubuntu20.04服务器使用教程(安装教程、常用命令、故障排查)持续更新中.....
安装教程(系统、NVIDIA驱动、CUDA、CUDNN、Pytorch、Timeshift、ToDesk) 制作U盘启动盘,并安装系统 在MSDN i tell you下载Ubuntu20.04 Desktop 版本,并使用Rufus制作UEFI启动盘,参考UEFI安装Ubuntu使用GPTUEFI模式安…...

访问学者J1签证的申请流程
访问学者J1签证是许多人前往美国进行学术研究和文化交流的重要途径之一。申请J1签证需要经过一系列步骤和程序,让知识人网小编带大家来了解一下申请流程吧。 首先,申请者需要确认自己符合J1签证的资格要求。这包括被美国的赞助机构或组织接受,…...

51单片机(STC8)-- GPIO输入输出
文章目录 I/O口相关寄存器端口数据寄存器端口模式配置寄存器(PxM0,PxM1)端口上拉电阻控制寄存器(PxPU)关于I/O的注意事项 配置I/O口I/O设置demoI/O端口模式LED控制(I/O输出)按键检测(I/O输入) S…...

【实用安装教程】在win系统下制作Mac OS镜像启动U盘
第一步:制作Mac OS系统引导镜像启动U盘 准备一个8G(或以上)的U盘插入到win系统的电脑上 去下载TransMac(Mac启动盘制作工具)v10.4按照说明安装好 插入准备好的U盘,U盘数据要转移,打开TransMac,右键U盘选…...

职场唠嗑-国家教学
文章目录 职场晋升潜规则:让上司看到自己工作能力职场生存指南:脆弱无罪,眼泪如何变利器关于具备谋取好职位的资格实习生在职场的基本“规矩”比能力更能决定人生的,是你对工作的态度跳槽:看别人家的“饭”端自家的碗职…...

【温故而知新】JavaScript数据结构详解
一、概念 JavaScript是一种弱类型的编程语言,它提供了一些内置的数据结构来存储和组织数据。 在计算机科学中,数据结构是一种特定的方式来组织和存储数据,以便于有效地访问和修改数据。在JavaScript中,数据结构是指相互之间存在…...

matlab如何标定相机内外参和畸变参数
关于内外参矩阵和畸变矩阵可以学习 https://blog.csdn.net/qq_30815237/article/details/87530011?spm1001.2014.3001.5506 在APP中找到 camera Calibrator 点击 Add Images,导入拍照图片。标定20张左右就够了,然后角度变一下,但不需要变太…...
【卫星科普】什么是农业一号卫星和农业二号卫星?
农业一号卫星和农业二号卫星是中国自主研发的两颗重要卫星,主要用于农业领域的监测和研究。 农业一号卫星是中国第一颗具备红边波段传感器的卫星,也是世界上第一颗具备红边波段的宽视场多光谱中高分辨率卫星。这对农业农村遥感监测非常重要,…...

imgaug库指南(一):从入门到精通的【图像增强】之旅
文章目录 引言imgaug简介安装和导入imgaug代码示例imgaug的强大之处和用途小结结尾 引言 在深度学习和计算机视觉的世界里,数据是模型训练的基石,其质量与数量直接影响着模型的性能。然而,获取大量高质量的标注数据往往需要耗费大量的时间和…...
vue封装基础input组件(添加防抖功能)
先看一下效果: // 调用页面 <template><div><!-- v-model:伪双向绑定 --><my-input v-model"inputVal" label"姓名" type"textarea" /></div> </template><script> import…...

小程序一次性订阅消息(消息通知):java服务端实现
文章目录 引言一、消息订阅1.1 小程序订阅消息功能介绍1.2 消息分类1.2.1 新版一次性订阅消息Beta1.2.2 一次性订阅消息(用户通过弹窗订阅)1.2.3 长期订阅消息(用户通过弹窗订阅)1.2.4 设备订阅消息 二、获取模板ID1.登录[微信公众…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

【版本控制】GitHub Desktop 入门教程与开源协作全流程解析
目录 0 引言1 GitHub Desktop 入门教程1.1 安装与基础配置1.2 核心功能使用指南仓库管理日常开发流程分支管理 2 GitHub 开源协作流程详解2.1 Fork & Pull Request 模型2.2 完整协作流程步骤步骤 1: Fork(创建个人副本)步骤 2: Clone(克隆…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

VASP软件在第一性原理计算中的应用-测试GO
VASP软件在第一性原理计算中的应用 VASP是由维也纳大学Hafner小组开发的一款功能强大的第一性原理计算软件,广泛应用于材料科学、凝聚态物理、化学和纳米技术等领域。 VASP的核心功能与应用 1. 电子结构计算 VASP最突出的功能是进行高精度的电子结构计算ÿ…...
无头浏览器技术:Python爬虫如何精准模拟搜索点击
1. 无头浏览器技术概述 1.1 什么是无头浏览器? 无头浏览器是一种没有图形用户界面(GUI)的浏览器,它通过程序控制浏览器内核(如Chromium、Firefox)执行页面加载、JavaScript渲染、表单提交等操作。由于不渲…...
