策略模式+责任链模式配合Nacos实现参数校验链
1、业务场景
在SpringBoot项目中,针对接收的参数信息,根据需求要进行以下校验:
- 校验客户的apikey是否合法;
- 校验请求的ip地址是否是白名单;
- 校验短信的签名;
- 校验短信的模板;
- 校验手机号的格式合法性;
- 校验客户剩余的金额是否充足。
2、实现分析
对于接口需要校验的参数和信息,为了保证校验的方式做到动态可插拔,而且有利于后期的扩展,参考了Mybatis二级缓存的源码,采用策略模式+责任链模式的套路。实现的大致流程是向上声明一个接口,提供校验方法,然后后编写多个校验的实现类,在执行校验时,会拿到所有的校验接口实现类,然后以责任链的形式一个个校验执行。而且,配合Nacos提供的配置动态刷新,指定校验链执行的内容,需要改变时,只需要修改Nacos的配置参数。
3、代码编写
下面是整个校验链路的代码骨架,不涉及校验条件的具体实现细节。
1. 校验的父接口
/*** 做策略模式的父接口*/
public interface CheckFilter {/*** 校验方法* @param obj*/void check(Object obj);}2. 准备校验的实现类
/*** 校验客户的apikey是否合法*/
@Service(value = "apikey")
@Slf4j
public class ApiKeyCheckFilter implements CheckFilter {@Overridepublic void check(Object obj) {log.info("【接口模块-校验apikey】");}
}/*** 校验请求的ip地址是否是白名单*/
@Service(value = "ip")
@Slf4j
public class IPCheckFilter implements CheckFilter {@Overridepublic void check(Object obj) {log.info("【接口模块-校验ip】");}
}/*** 校验短信的签名*/
@Service(value = "sign")
@Slf4j
public class SignCheckFilter implements CheckFilter {@Overridepublic void check(Object obj) {log.info("【接口模块-校验签名】");}
}/*** 校验短信的模板*/
@Service(value = "template")
@Slf4j
public class TemplateCheckFilter implements CheckFilter {@Overridepublic void check(Object obj) {log.info("【接口模块-校验模板】");}
}/*** 校验手机号的格式合法性*/
@Service(value = "mobile")
@Slf4j
public class MobileCheckFilter implements CheckFilter {@Overridepublic void check(Object obj) {log.info("【接口模块-校验手机号】");}
}/*** 校验客户剩余的金额是否充足*/
@Service(value = "fee")
@Slf4j
public class FeeCheckFilter implements CheckFilter {@Overridepublic void check(Object obj) {log.info("【接口模块-校验客户余额】");}
}
3. 准备上下文对象,拿到所有的校验接口实现类
/*** 策略模式的上下文对象*/
@Component
@RefreshScope
public class CheckFilterContext {// Spring的IOC会将对象全部都放到Map集合中// 基于4.x中Spring提供的反省注解,基于Map只拿到需要的类型对象即可@Autowiredprivate Map<String,CheckFilter> checkFiltersMap;// 基于Nacos获取到执行的顺序和需要执行的校验对象@Value("${filters:apikey,ip,sign,template}")private String filters;/*** 当前check方法用于管理校验链的顺序*/public void check(Object obj){//1. 将获取到filters基于,做切分String[] filterArray = filters.split(",");//2. 遍历数组即可for (String filter : filterArray) {CheckFilter checkFilter = checkFiltersMap.get(filter);checkFilter.check(obj);}}
}4. Nacos配置校验执行顺序
# 校验策略的执行内容和顺序 apikey,ip,sign,template,mobile,fee
filters: apikey,ip,sign,template,mobile,fee5. 上下文对象的使用
@RestController
public class CheckController{@Autowiredprivate CheckFilterContext checkFilterContext;/*** 测试使用 */@PostMappingpublic void check(Object obj){checkFilterContext.check(obj);}
}相关文章:

策略模式+责任链模式配合Nacos实现参数校验链
1、业务场景 在SpringBoot项目中,针对接收的参数信息,根据需求要进行以下校验: 校验客户的apikey是否合法;校验请求的ip地址是否是白名单;校验短信的签名;校验短信的模板;校验手机号的格式合法…...

‘react-native‘ 不是内部或外部命令,也不是可运行的程序或批处理文件。
原因:没有下载react-native 解决下载react-native npm i -g react-native-cli...
c语言:求最小公倍数|练习题
一、题目 输入两个数,求两数的最小公倍数。 如图: 二、思路分析 1、先知道两个数里的最小值(比如:9和6,取6) 2、用2到6,5个数,同时除以9和6,得最小公约数:3 3、用9除33,6除32。得最小…...
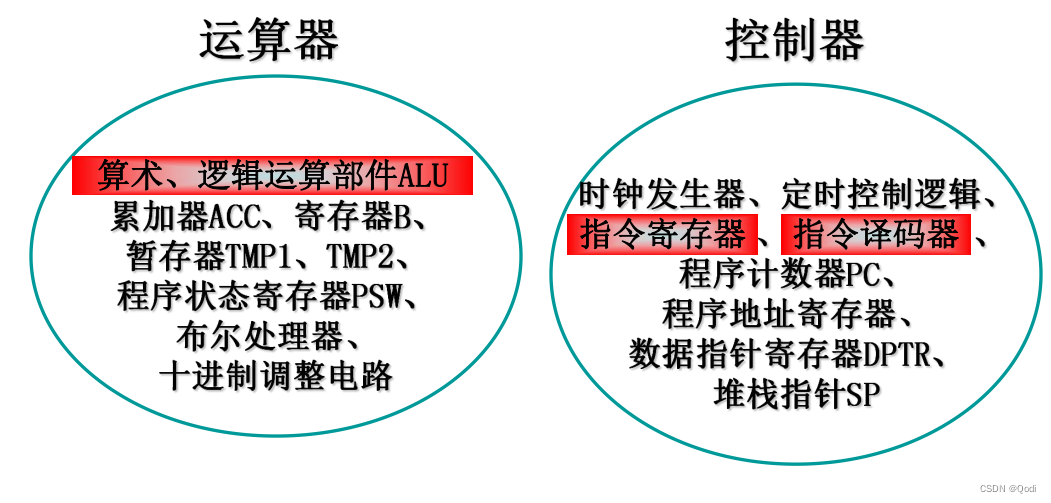
嵌入式系统(二)单片机基础 | 单片机特点 内部结构 最小系统 电源 晶振 复位
上一篇文章我们介绍了嵌入式系统 嵌入式系统(Embedded System)是一种特定用途的计算机系统,它通常嵌入在更大的产品或系统中,用于控制、监测或执行特定的任务。这些系统通常由硬件和软件组成,旨在满足特定的需求&…...

NLP基础——中文分词
简介 分词是自然语言处理(NLP)中的一个基本任务,它涉及将连续的文本序列切分成多个有意义的单元,这些单元通常被称为“词”或“tokens”。在英语等使用空格作为自然分隔符的语言中,分词相对简单,因为大部分…...

阿里云服务器Alibaba Cloud Linux 3镜像版本大全说明
Alibaba Cloud Linux阿里云打造的Linux服务器操作系统发行版,Alibaba Cloud Linux完全兼容完全兼容CentOS/RHEL生态和操作方式,目前已经推出Alibaba Cloud Linux 3,阿里云百科aliyunbaike.com分享Alibaba Cloud Linux 3版本特性说明ÿ…...

WebGIS开发的常见框架及优缺点
WebGIS开发引擎的发展历程: 内容来自公众号:Spatial Data 地图API分类 WebGIS系统通常都围绕地图进行内容表达,但并不是有地图就一定是WebGIS,所以下面要讨论下基于Web的地图API分类及应用场景。Web上的Map API主要分类ÿ…...
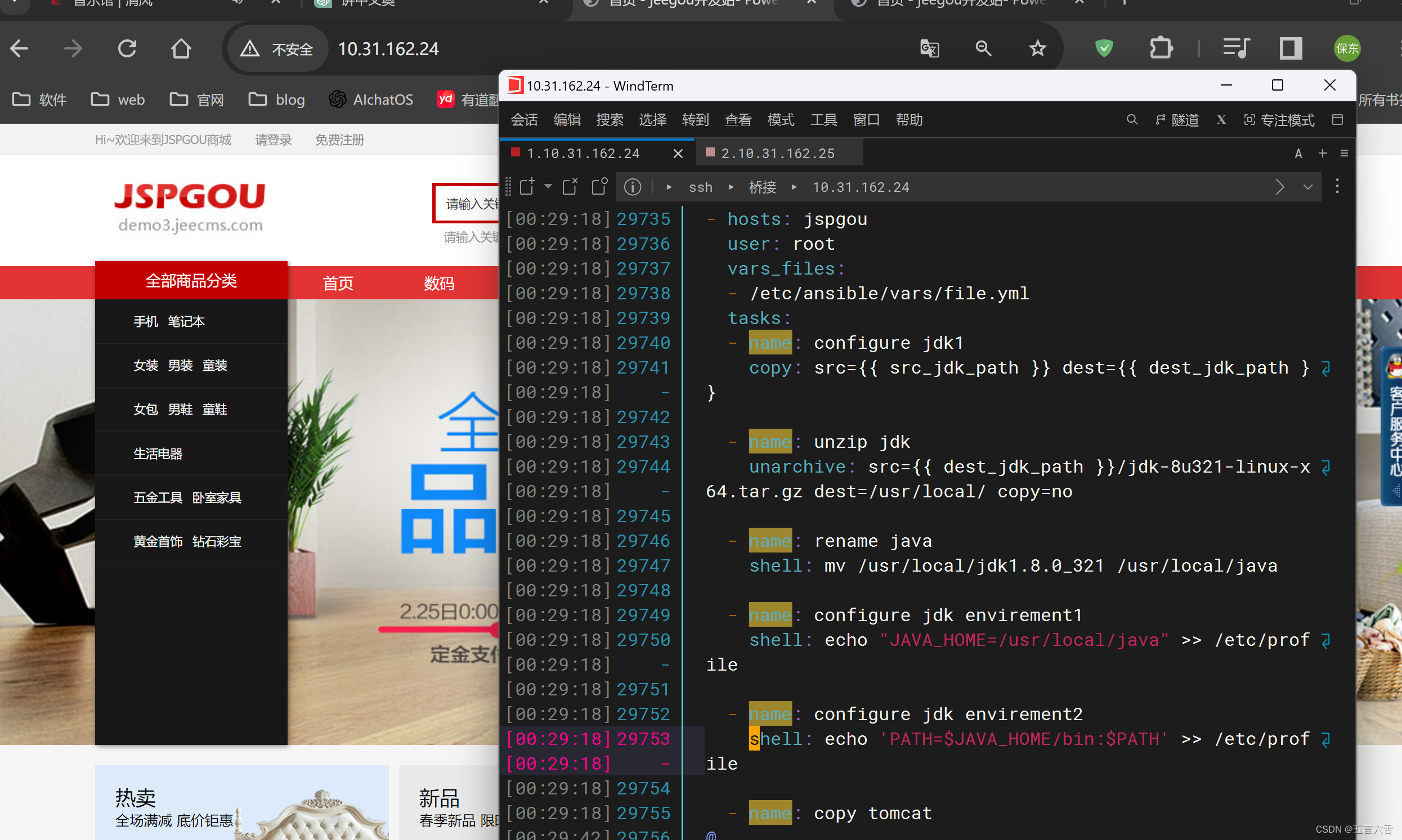
ansible 配置jspgou商城上线(MySQL版)
准备环境 准备两台纯净的服务器进行,在实验之前我们关闭防火墙和selinux systemctl stop firewalld #关闭防火墙 setenforce 0 #临时关闭selinux hosts解析(两台服务器都要去做) [rootansible-server ~]# vim /etc/hosts 10.31.162.24 ansible-ser…...
算法导论复习——CHP22 分支限界法
LIFO和FIFO分枝-限界法 采用宽度优先策略,在生成当前E-结点全部儿子之后再生成其它活结点的儿子,且用限界函数帮助避免生成不包含答案结点子树的状态空间的检索方法。两种基本设计策略: FIFO检索:活结点表采用队列&#x…...

鸿蒙系列--装饰器
一、基础UI组件结构 每个UI组件需要定义为Component struct对象,其内部必须包含一个且只能包含一个build(){}函数,用于绘制UI;struct之内、build()函数之外的地方用于存放数据。 二、基本UI装饰器 Entry 装饰struct,页面的入口…...

FairGuard游戏加固产品常见问题解答
针对日常对接中,各位用户对FairGuard游戏加固方案在安全性、稳定性、易用性、接入流程等方面的关注,我们梳理了相关问题与解答,希望可以让您对产品有一个初步的认知与认可。 Q1:FairGuard游戏加固产品都有哪些功能? A:FairGuar…...

Redis(二)数据类型
文章目录 官网备注十大数据类型StringListHashSetZSetBitmapHyperLogLog:GEOStreamBitfield 官网 英文:https://redis.io/commands/ 中文:http://www.redis.cn/commands.html 备注 命令不区分大小写,key区分大小写帮助命令help…...
)
2023年广东省网络安全B模块(笔记详解)
模块B 网络安全事件响应、数字取证调查和应用安全 一、项目和任务描述: 假定你是某网络安全技术支持团队成员,某企业的服务器系统被黑客攻击,你的团队前来帮助企业进行调查并追踪本次网络攻击的源头,分析黑客的攻击方式,发现系统漏洞,提交网络安全事件响应报告,修复系统…...
每日力扣算法题(简单篇)
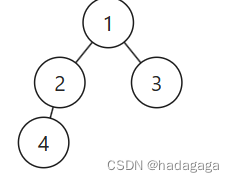
543.二叉树的直径 原题: 给你一棵二叉树的根节点,返回该树的 直径 。 二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。 两节点之间路径的 长度 由它们之间边数表示。 解题思路: …...
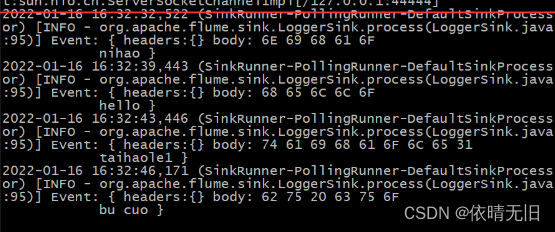
Flume基础知识(三):Flume 实战监控端口数据官方案例
1. 监控端口数据官方案例 1)案例需求: 使用 Flume 监听一个端口,收集该端口数据,并打印到控制台。 2)需求分析: 3)实现步骤: (1)安装 netcat 工具 sudo yum …...

通过IP地址如何进行网络安全防护
IP地址在网络安全防护中起着至关重要的作用,可以用于监控、过滤和控制网络流量,识别潜在威胁并加强网络安全。以下是通过IP地址进行网络安全防护的一些建议: 1. 建立IP地址白名单和黑名单: 白名单:确保只有授权的IP地…...

Vue.js 中使用 Watch 选项实现动态问题判断与展示答案
组件结构 以下是组件的基本结构: <template><div><!-- 输入框,用于输入问题 --><p>提出一个是/否问题:<input v-model"question" :disabled"loading" /></p><!-- 显示答案 --&…...

python笔记-自用
2024/1/3# python用号实现字符串的拼接,非字符串不能拼接 from pymysql import Connection# 连接mysql数据库salary 100 name "wang"ans "%s" % salary name print(ans)x 1 y 2 sum "%s %s" % (x, y) print(sum)# %s字符串占…...

安克创新与火山引擎数智平台开展合作:数据分析降门槛 数据协同破边界
更多技术交流、求职机会,欢迎关注字节跳动数据平台微信公众号,回复【1】进入官方交流群 近日,消费电子品牌安克创新与火山引擎数智平台(VeDI)达成合作,双方将聚焦安克创新大数据平台的海量数据分析场景&…...
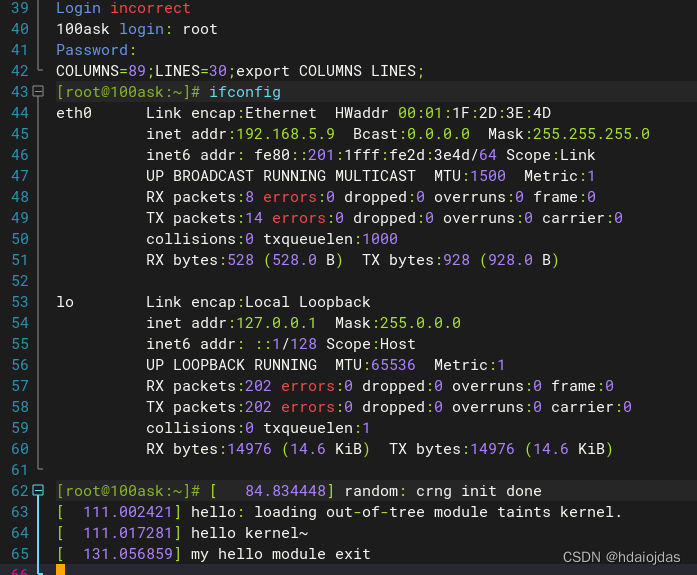
LDD学习笔记 -- Linux内核模块
LDD学习笔记 -- 内核模块 简介LKM类型Static Linux Kernel ModuleDynamic Linux Kernel ModuleLKM编写语法 syntax详细描述内核头文件用户空间头文件Module Initialization FunctionModule Cleanup FunctionKeyword & Tag宏 __init __exitLKM入口注册Module Metadate&#…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...
