正定矩阵在格密码中的应用(知识铺垫)
目录
一. 写在前面
二. 最小值点
三. 二次型结构
四. 正定与非正定讨论
4.1 对参数a的要求
4.2 对参数c的要求
4.3 对参数b的要求
五. 最小值,最大值与奇异值
5.1 正定型(positive definite)
5.2 负定型(negative definite)
5.3 奇异型
六. 鞍点(saddle point)
七. 矩阵二次型
7.1 介绍
7.2 举例
例题1
例题2
例题3
八. 正定矩阵与格密码
一. 写在前面
格密码中有时要求格基矩阵是正定的,本文章将从方程和矩阵角度来解释正定性,辅助格密码的理解。
推荐可以先看下这篇文章:
格密码与线性代数-CSDN博客
对称矩阵一定有实数特征值(real eigenvalue),本文章尝试在不计算矩阵特征值的情况下,快速判断矩阵特征值是否全为正数,其中涉及三个矩阵的基本概念:矩阵的主元(pivot),行列式,特征值。
二. 最小值点
在微分方程中,如果特征值为负数,那么以下函数单调递减:
在密码学或计算机领域的优化问题(optimization)经常需要判断N维情况下的最小值,数学知识告诉我们这与二阶导(second derivative test)相关,举两个例子:

尝试求这两个二维函数的最小值。
首先可计算:
很明显,最小值肯定要求一阶导数为0,也就是所谓的关注linear term,发现(0,0)该点符合要求,如下:

也就是(0,0)为这两个函数的极值点(stationary point)。
第一个平面z=F(x,y)与水平面z=7相切;
第二个平面z=f(x,y)与水平面z=0相切;
一阶导分析完毕来看下在(0,0)位置的二阶导,如下:
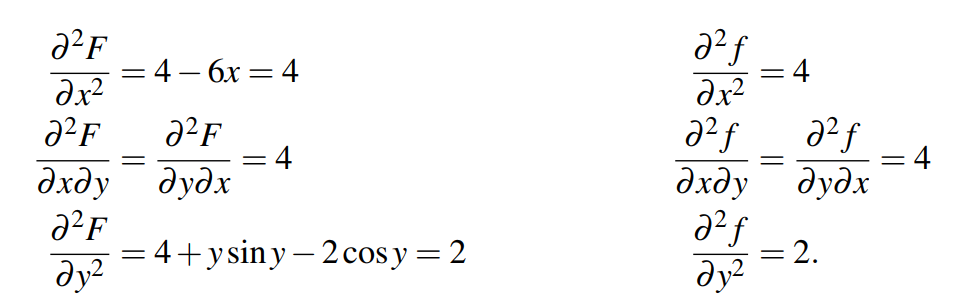
这两个二维函数的二阶导值一样,说明两个函数的性质相同。实际上F(x,y)的最高次幂为,所以其最小值为
,接下来我们把重心放在f(x,y)。
三. 二次型结构
以上讨论中f(x,y)的形式为二次型:
易得在(0,0)处,该类函数的一阶微分:
也就是该类二次型,原点一定是其极值点。
如果极小值点(local minimum)也是最小值点(global minimum),那么可得此类平面的图形像一个碗,碗的底部就是原点,如下图:
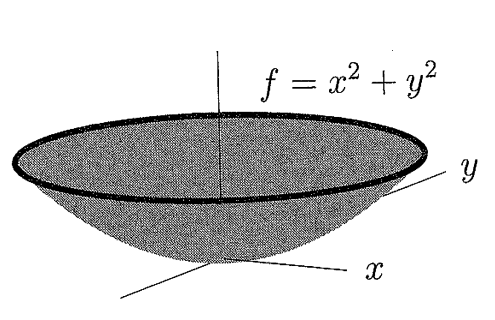
如果极值点不在原点处,而在其他任意点处,比如在,其二阶导如下:

除了原点外,如果函数严格为正数,那么称之为正定(positive definite)。
四. 正定与非正定讨论
对于单变量的函数来讲,二阶大于0,函数拥有最小值,如下:
反之,则函数有最大值。
对于二维函数来讲,函数拥有三个二阶导函数:
期待利用这三个数来判断函数拥有最小值还是最大值。
目标:什么情况下,二次型为正定的?
4.1 对参数a的要求
当x=1,y=0时,可得:
正定性要求a为正数,利用导数的观点解释则是:
也就是该曲面沿着x轴向上弯曲。
4.2 对参数c的要求
当x=0时,沿着y轴方向可得:
很明显正定性要求c>0
举两个简单例子,大家可以快速判断下:
例1
例2
解:
例1非正定,因为
例2非正定,因为
4.3 对参数b的要求
将二次型结构转变为如下完全平方差形式:

观察右边第二项,要想函数正定,则必须:
也就是:
五. 最小值,最大值与奇异值
5.1 正定型(positive definite)
根据以上讨论,要想二次型为正定,需要满足:
如果要求某点处的最小值,那么:
并且要求:
5.2 负定型(negative definite)
负定型的要求与正定型刚好相反,如下:
由此可求该函数的最大值
5.3 奇异型
当a,b,c满足:
易得当a>0时,该函数为半正定(positive semi-definite)
当a<0时,该函数为半负定(negative semi-definite)
也就是当x=b,y=-a时,该函数可以取0。原始的平面z=f(x,y)像一个碗,奇异情况下像一个山谷,举例:
六. 鞍点(saddle point)
鞍点要求:
举例两个函数:

来看一个图像:

这种二次型既可以取正数,也可以取负数,所以为非定型(indifinite)。从图形上看,此时的极值点既不是最小值,也不是最大值,该点则被称之为鞍点(saddle point)。
七. 矩阵二次型
7.1 介绍
总结以上我们发现,二阶导数其实可以形成一个对称矩阵。将和
放在对角线,将2bxy分成一半,放在剩下的两个位置上,由此二次型函数f(x,y)即可以表示成一个2行2列的矩阵,如下:

将此处的2维扩展到n维,便可以从矩阵的角度来理解函数的最大值与最小值。假定有n个变量,将其写成列向量x的形式,那么对任意对称矩阵A,矩阵向量相乘与二次型之间是互相等效的,如下:
更具体来讲,如下:

对角线的元素与
相乘。对称形式
合并后再相乘可得
,即可以还原函数为:
注意每一项都是二次型,当时,函数的一阶导函数一定为0.该函数的切面是水平的,也就是其极值点。、
借助此理论即可判断当向量x为0时,函数存在最大值,最小值,还是鞍点。
7.2 举例
例题1
函数,其对应矩阵如下:
很明显为鞍点
例题2
函数f=2xy,其对应矩阵:
很明显鞍点
例题3
给定函数如下:
该函数拥有最小值,写成矩阵格式如下:

其实矩阵A可以看成二阶导的矩阵,也就是满足:
同理可得:
从这个角度也可以理解矩阵A为对称矩阵,很明显当原函数存在最小值时,矩阵A则为正定的。
八. 正定矩阵与格密码
正定矩阵与特征值有关,格基特征值的大小会影响格密码中光滑参数的大小,从而影响安全性。具体这方面的知识会陆续更新。
相关文章:
正定矩阵在格密码中的应用(知识铺垫)
目录 一. 写在前面 二. 最小值点 三. 二次型结构 四. 正定与非正定讨论 4.1 对参数a的要求 4.2 对参数c的要求 4.3 对参数b的要求 五. 最小值,最大值与奇异值 5.1 正定型(positive definite) 5.2 负定型(negative defin…...
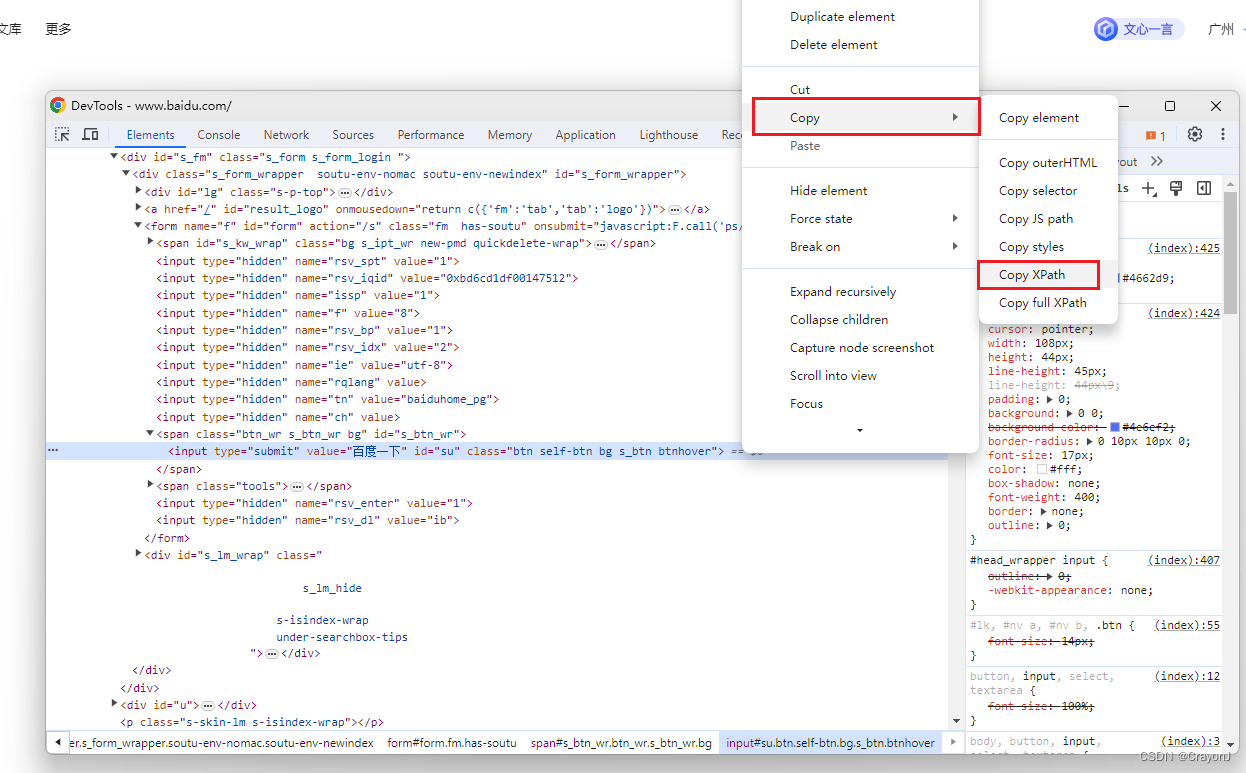
关于使用Selenium获取网页控制台的数据
背景: 需要获取网页的控制台的数据,如下图 在此文章将使用到 Pycharm 和 Selenium4 Pycharm安装 Selenium安装 from selenium import webdriver from selenium.webdriver.common.by import By import time# 创建浏览器对象 browser webdriver.Chro…...

vue2和vue3中的路由使用及传参方式
文章目录 vue2中使用路由Vue3 中使用路由路由传参方式 Vue 2 和 Vue 3 中的路由系统有很多相似之处,但也存在一些重要的区别。下面将分别介绍 Vue 2 和 Vue 3 中的路由使用方式,并了解下它们之间的不同之处。 vue2中使用路由 在 Vue 2 中,通…...

论文管理器
论文管理器 这个论文管理器仍然存在许多漏洞。目前,通过按照一些例行程序操作,它可以正常工作。我将在有时间的时候改进代码,提供详细说明,并添加新功能。当该管理器的代码进行优化后,我会上传到github上。 一个建立…...

postfix配置tls加密
1.编译安装 编译安装openss【卸载原有openssl,然后下载新的安装,因为postfix需要新版本openssl】编译安装postfix,下面这行命令 make -f Makefile.init makefiles CCARGS"-DHAS_MYSQL -I/www/server/mysql/include -DUSE_SASL_AUTH -I/usr/include…...

虚拟专线网络(IP-VPN)
虚拟专线网络(IP-VPN),因为它的安全性和可靠性。通过亚洲领先的 IP VPN 提供商。享受更高的可管理性和可扩展性,在多个站点之间交付 IP 流量或数据包,拥有亚太地区最大的 IP 骨干网。 1,保证正常运行时间,在网络链路发…...

【Unity动画系统】Unity动画系统Animation详解,参数细节你是否弄清?
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:Uni…...

K8S Helm安装RocketMQ standalone单机版,配置外网地址注册到nameserver中方便本地开发
K8S Helm安装RocketMQ standalone单机版,配置外网地址注册到nameserver中方便本地开发 helm地址 rocketmq 3.0.2 sir5kong/rocketmq helm repo add rocketmq https://helm-charts.itboon.top/rocketmq helm pull rocketmq/rocketmq tar -xvf rocketmq-3.0.2.t…...
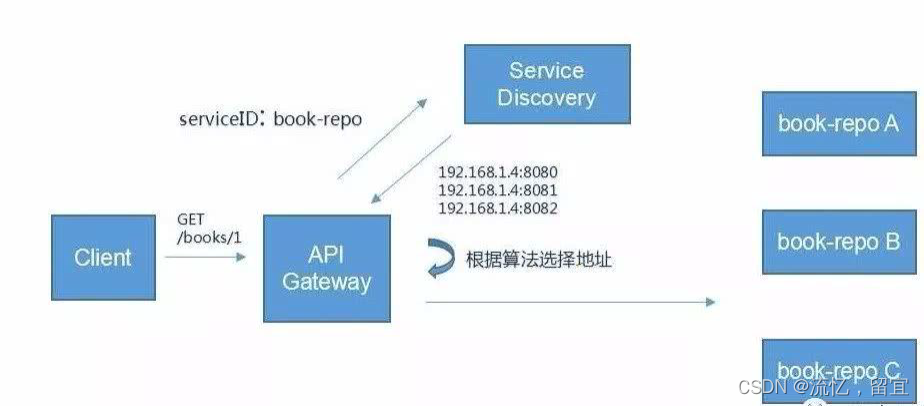
分布式基础概念
分布式基础概念 1 微服务 微服务架构风格,就像是把一个单独的应用程序开发为一套小服务,每个小服务运行在自己的进程中,并使用轻量级机制通信,通常是HTTP API。这些服务围绕业务能力来构建,并通过完全自动化部署机制…...
)
蓝桥杯python比赛历届真题99道经典练习题 (89-99)
【程序89】 题目:某个公司采用公用电话传递数据,数据是四位的整数,在传递过程中是加密的,加密规则如下: 每位数字都加上5,然后用和除以10的余数代替该数字,再将第一位和第四位交换,第二位和第三位交换。 1.程序分析: 2.程序源代码: from sys import stdout if __n…...
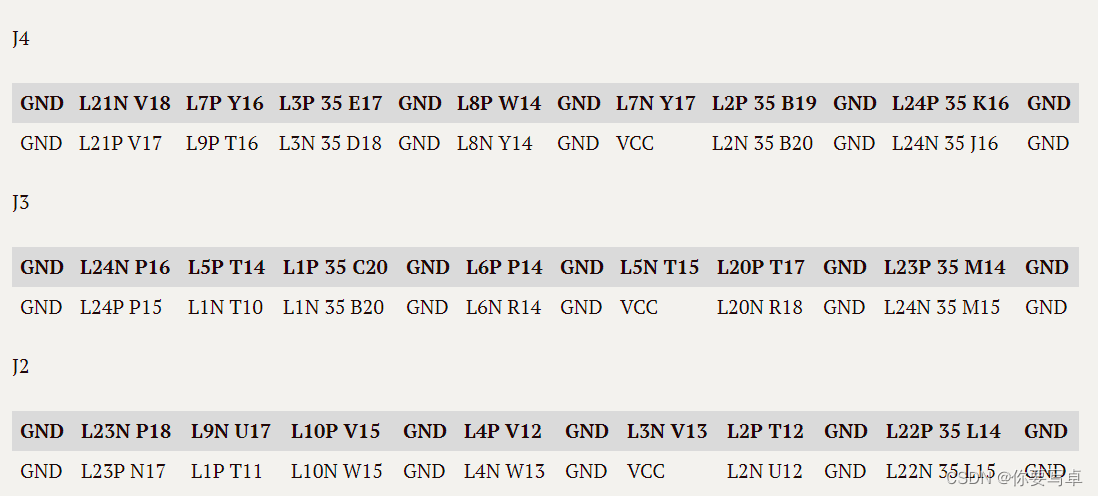
蚂蚁矿机AntMiner T9+引出IO定义
这个板子只有s9的原理图参考,大部分一样但是也有很多改动。 下面是自己测出来的IO。全部为PL,没有PS引出。 共计56个引脚可用,但是不是都是完整的差分对,而且显然有些走线没办法高速跑。 测试方法 万用表先区分VCC GND和IO(对地…...

浅析 Dockerfile 构建缓存:原理与优化方法
Docker镜像的分层结构 Docker镜像是由一层一层的文件系统组成,UnionFS将这些镜像层堆叠在一起镜像层是只读的,构建完成后就不能更改了,即使在新的镜像层修改或删除了某些文件,也不会影响之前的镜像层内容用Dockerfile构建镜像时&…...
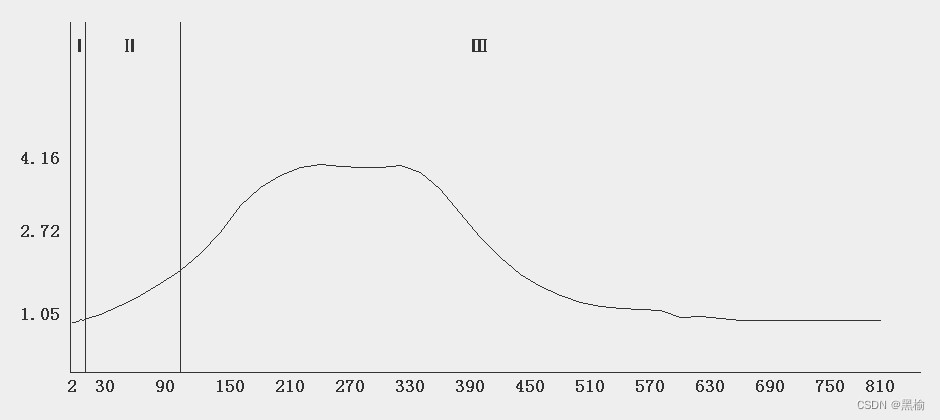
隐藏层节点数对分类准确率的影响
直线上有9个格子,4个石子, 数量 结构编号 6 0 1 1 1 1 0 0 0 0 0 5 2 1 1 1 0 1 0 0 0 0 5 1 1 0 1 1 1 0 0 0 0 4 3 1 1 0 0 1 1 0 0 0 4 4 1 0 1 0 1 1 0 0 0 3 5 1 0 1 0 1 0 1 0…...

【水浸传感器】软硬件一体水浸监测整套方案远程监测解决各种环境漏水问题
一、痛点分析 在工业生产中,水浸传感器可以安装在数据中心、半导体厂房、输油管道、车间仓库、变电室等易发生水浸的区域。一旦检测到漏水情况,立即发出信号反馈。然而,水浸传感器分散在各个地点,导致管理不集中、不便捷…...
知虾会员**成为知虾会员,尊享专属权益**
在当今繁忙的生活中,线上购物已经成为现代人们的主要消费方式之一。而作为线上购物平台的领军者之一,Shopee为了提供更加个性化和便利的购物体验,推出了知虾会员(Shopee会员)服务。知虾会员不仅可以享受到一系列会员专…...

好代码网同款wordpress主题,适合搭建资源分享类网站,自带五六百的精品资源数据
代码简介: 好代码资源网是个还不错的资源分享类网站,基于wordpress搭建的。它的主题看起来还是不错的。这里分享一下这个网站的主题包。说是主题包,其实就是整站打包的,集成了主题(wordpress美化主题包几个插件&#…...

Java多线程<三>常见的多线程设计模式
多线程的设计模式 两阶段线程终止 park方法 interrupted() 会让他失效。 使用volatile关键字进行改写 单例模式 双锁检测 保护性暂停 实现1: package threadBase.model;/*** author: Zekun Fu* date: 2022/5/29 19:01* Description:* 保护性暂停,* …...

JavaScript 基础二part1.运算符:赋值、一元、比较、逻辑运算符
JavaScript 基础二 1.1 赋值运算符1.2 一元运算符自增运算符的用法:例题 1.3 比较运算符不同类型间的比较严格相等对 null 和 undefined 进行比较 1.4 逻辑运算符例题 1.5 运算符优先级 1.1 赋值运算符 赋值运算符:对变量进行赋值的运算符 已经学过的赋…...
Linux 进程(八) 进程的退出码
main 函数的返回值叫做进程的退出码。当进程成功退出的时候,我们一般用0来表示。进程失败的时候一般用非零来表示。我们使用不同的数字来表示进程退出时不同的失败原因。 我们查看系统的有多少退出码以及其含义时需要用到strerror() 他的头文件和用法如下。 通过一…...

Go语言中支持的internal目录配置与组织内私网包配置详解
Go 中的内部包 这里可能会有歧义 可能是 Go 的 internal 目录中的包也可能是指内部开发的包 函数和变量的可见性 对于函数和变量而言,有如下规则:1 )小写字母开头的函数变量结构体只能在本包内访问2 )大写字母开头的函数变量结…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
