【Py/Java/C++三种语言OD2023C卷真题】20天拿下华为OD笔试之【数学】2023C-素数之积【欧弟算法】全网注释最详细分类最全的华为OD真题题解
文章目录
- 题目描述与示例
- 题目描述
- 输入描述
- 输出描述
- 示例
- 输入
- 输出
- 说明
- 解题思路
- 暴力解
- 质数筛
- 代码
- Python
- Java
- C++
- 时空复杂度
- 华为OD算法/大厂面试高频题算法练习冲刺训练
题目描述与示例
题目描述
RSA加密算法在网络安全世界中无处不在,它利用了极大些数因数分解的闲难度,数据越大,安全系数越高,给定一个32位整数,请对其进行因数分解,找出是哪两个素数的乘积。
输入描述
1`个正整数`num
0 < num <= 2147483647
输出描述
如果成功找到,以单个空格分割,从小到大输出两个素数。分解失败,请输出-1 -1
示例
输入
15
输出
3 5
说明
因数分解后,找到两个素数3和5,使得3*5=15,按从小到大排列后,输出3 5
解题思路
经典的大数分解问题。
关于素数相关的内容,可以详看算法题中常用数学概念、公式、方法汇总 里的相关部分。
暴力解
比较容易想到的暴力解法包含以下步骤
- 从小到大枚举所有小于
sqrt(num)的数a - 判断
num是否可以整除a,若- 不可以,则直接跳过。遍历下一个
a - 可以,则进行后续判断
- 不可以,则直接跳过。遍历下一个
- 判断
a是否是素数,若- 不是,则直接跳过。遍历下一个
a - 是,则进行后续判断
- 不是,则直接跳过。遍历下一个
- 判断
b = num // a是否是素数,若- 不是,则直接跳过。遍历下一个
a - 是,则
a b为答案。
- 不是,则直接跳过。遍历下一个
上述过程慢的原因主要在于,计算a或b是否是素数的环节。
可以使用质数筛来优化上述过程。
质数筛
使用质数筛解决上述大数分解的过程如下
- 构建长度为
num+1的质数筛数组sieve。sieve[i]是True表示i是质数,sieve[i]是False表示i是合数。 - 枚举质数筛中每一个质数
a,即sieve[a] = True的下标。 - 判断
num是否可以整除a,若- 不可以,则直接跳过。遍历下一个
a - 可以,则进行后续判断
- 不可以,则直接跳过。遍历下一个
- 判断
b = num // a是否是素数,若- 不是,则直接跳过。遍历下一个
a - 是,则
a b为答案。
- 不是,则直接跳过。遍历下一个
代码
Python
# 题目:【模拟】2023C-素数之积
# 分值:100
# 作者:许老师-闭着眼睛学数理化
# 算法:数学
# 代码看不懂的地方,请直接在群上提问from math import floor, sqrt# 使用埃氏筛计算数组
def sieve_of_eratosthenes(n):# 构建埃氏筛,长度为n+1,初始化均为True,表示默认为质数sieve = [True] * (n + 1)# 0和1不是质数sieve[0], sieve[1] = False, False# 枚举从2到floor(sqrt(x))的每一个数xfor x in range(2, floor(sqrt(n)) + 1):# 如果x是一个质数,则说明其m倍(m >= 2)的所有正整数是合数if sieve[x] == True:# 将mx标记为Falsefor i in range(2 * x, n + 1, x):sieve[i] = False# 退出循环后,sieve中所有为True的元素下标为质数primes = [i for i in range(n + 1) if sieve[i]]return primesnum = int(input())
# 计算所有小于num的素数
primes = sieve_of_eratosthenes(num)
primes_set = set(primes)# 初始化一个标记,表示是否找到一组素数
isFind = False
# 遍历所有小于num的素数a
for a in primes:# 如果num可以整除aif num % a == 0:# 则计算b是否也是素数b = num // a# 如果是,则输出(a, b)# 同时标记isFind为True,表示计算得到一组答案# 同时退出循环if b in primes_set:print(a, b)isFind = Truebreak# 如果退出循环后,isFind仍为False,则输出(-1, -1)
if isFind == False:print(-1, -1)
Java
import java.util.*;public class Main {public static List<Integer> sieveOfEratosthenes(int n) {boolean[] sieve = new boolean[n + 1];Arrays.fill(sieve, true);sieve[0] = sieve[1] = false;for (int x = 2; x * x <= n; ++x) {if (sieve[x]) {for (int i = x * x; i <= n; i += x) {sieve[i] = false;}}}List<Integer> primes = new ArrayList<>();for (int i = 2; i <= n; ++i) {if (sieve[i]) {primes.add(i);}}return primes;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int num = scanner.nextInt();List<Integer> primes = sieveOfEratosthenes(num);Set<Integer> primesSet = new HashSet<>(primes);boolean isFind = false;for (int a : primes) {if (num % a == 0) {int b = num / a;if (primesSet.contains(b)) {System.out.println(a + " " + b);isFind = true;break;}}}if (!isFind) {System.out.println("-1 -1");}}
}
C++
#include <iostream>
#include <vector>
#include <cmath>
#include <unordered_set>std::vector<int> sieve_of_eratosthenes(int n) {std::vector<bool> sieve(n + 1, true);sieve[0] = sieve[1] = false;for (int x = 2; x * x <= n; ++x) {if (sieve[x]) {for (int i = x * x; i <= n; i += x) {sieve[i] = false;}}}std::vector<int> primes;for (int i = 2; i <= n; ++i) {if (sieve[i]) {primes.push_back(i);}}return primes;
}int main() {int num;std::cin >> num;std::vector<int> primes = sieve_of_eratosthenes(num);std::unordered_set<int> primes_set(primes.begin(), primes.end());bool isFind = false;for (int a : primes) {if (num % a == 0) {int b = num / a;if (primes_set.find(b) != primes_set.end()) {std::cout << a << " " << b << std::endl;isFind = true;break;}}}if (!isFind) {std::cout << -1 << " " << -1 << std::endl;}return 0;
}
时空复杂度
时间复杂度:O(Nlog(NlogN))。构建质数筛所需要的时间
空间复杂度:O(1)。除了输入的序列,仅需若干常数变量维护遍历过程。
华为OD算法/大厂面试高频题算法练习冲刺训练
-
华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名!目前已服务100+同学成功上岸!
-
课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化
-
每期人数维持在20人内,保证能够最大限度地满足到每一个同学的需求,达到和1v1同样的学习效果!
-
60+天陪伴式学习,40+直播课时,300+动画图解视频,300+LeetCode经典题,200+华为OD真题/大厂真题,还有简历修改、模拟面试、专属HR对接将为你解锁
-
可上全网独家的欧弟OJ系统练习华子OD、大厂真题
-
可查看链接 大厂真题汇总 & OD真题汇总(持续更新)
-
绿色聊天软件戳
od1336了解更多
相关文章:

【Py/Java/C++三种语言OD2023C卷真题】20天拿下华为OD笔试之【数学】2023C-素数之积【欧弟算法】全网注释最详细分类最全的华为OD真题题解
文章目录 题目描述与示例题目描述输入描述输出描述示例输入输出说明 解题思路暴力解质数筛 代码PythonJavaC时空复杂度 华为OD算法/大厂面试高频题算法练习冲刺训练 题目描述与示例 题目描述 RSA加密算法在网络安全世界中无处不在,它利用了极大些数因数分解的闲难…...

uniapp路由
1、路由登记 uni-app页面路由为框架统一管理,开发者需要在pages.json里配置每个路由页面的路径及页面样式。 类似小程序在 app.json 中配置页面路由一样。 所以 uni-app 的路由用法与 Vue Router 不同,如仍希望采用 Vue Router 方式管理路由,…...

湖南大学-数据库系统-2023期末考试【原题】
前言 早上11:00考完的考试,下午回来打了三把LOL之后,凭着回忆把题目重现出来了。 在复习的时候刷了15,16,17,18,19,21六年的卷子,感觉题目都差不多,但是难度…...

【Java EE初阶九】多线程案例(线程池)
一、线程池的引入 引入池---->主要是为了提高效率; 最开始,进程可以解决并发编程的问题,但是代价有点大了,于是引入了 “轻量级进程” ---->线程 线程也能解决并发编程的问题,而且线程的开销比进程要小的多&…...
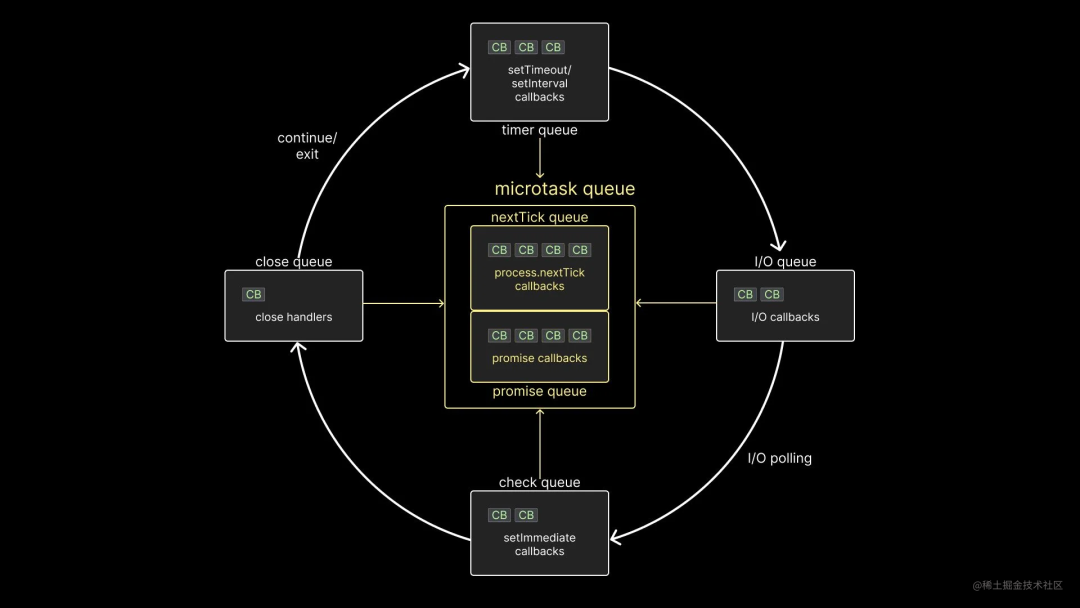
理解 Node.js 中的事件循环
你已经使用 Node.js 一段时间了,构建了一些应用程序,尝试了不同的模块,甚至对异步编程感到很舒适。但是有些事情一直在困扰着你——事件循环(Event Loop)。 如果你像我一样,花费了无数个小时阅读文档和观看…...

Mac 软件出现「意外退出」及「打不开」解决方法
Mac 软件出现「意外退出」及「打不开」解决方法 软件出现意外退出及软件损坏的情况,这是因为苹果删除了TNT的证书,所以大部分TNT破解的Mac软件会出现无法打开,提示意外退出。 终端需先安装Xcode或Apple命令行工具 如未装Xcode可以使用下列命…...

随机森林 3(代码)
通过随机森林 1和随机森林 2 的介绍,相信大家对理论已经了解的很透彻,接下来带大家敲一下代码,不懂得可以加我入群讨论。 第一份代码是比较原始的代码,第二份代码是第一段代码中引用的primitive_plot,第三份代码是使用…...

勒索事件急剧增长,亚信安全发布《勒索家族和勒索事件监控报告》
近期(12.15-12.21)态势快速感知 近期全球共发生了247起攻击和勒索事件,勒索事件数量急剧增长。 近期需要重点关注的除了仍然流行的勒索家族lockbit3以外,还有本周top1勒索组织toufan。toufan是一个新兴勒索组织,本周共发起了108起勒索攻击&a…...

LeetCode1523. Count Odd Numbers in an Interval Range
文章目录 一、题目二、题解 一、题目 Given two non-negative integers low and high. Return the count of odd numbers between low and high (inclusive). Example 1: Input: low 3, high 7 Output: 3 Explanation: The odd numbers between 3 and 7 are [3,5,7]. Exam…...

E中国铜金属行业需求前景及未来发展机遇分析报告2024-2030年
E中国铜金属行业需求前景及未来发展机遇分析报告2024-2030年 &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& 《报告编号》: BG471816 《出…...

python SVM 保存和加载模型参数
在 Python 中,你可以使用 scikit-learn 库中的 joblib 或 pickle 模块来保存和加载 SVM 模型的参数。以下是一个简单的示例代码,演示了如何使用 joblib 模块保存和加载 SVM 模型的参数: 保存模型参数: from sklearn import svm …...

JAVA进化史: JDK12特性及说明
JDK 12于2019年3月发布。这个版本相对于之前的版本来说规模较小,主要集中在一些改进和实验性的特性上。以下是JDK 12的一些主要特性: 引入了实验性的Shenandoah垃圾收集器 JDK 12引入了实验性的Shenandoah垃圾收集器,旨在实现极低的暂停时间…...
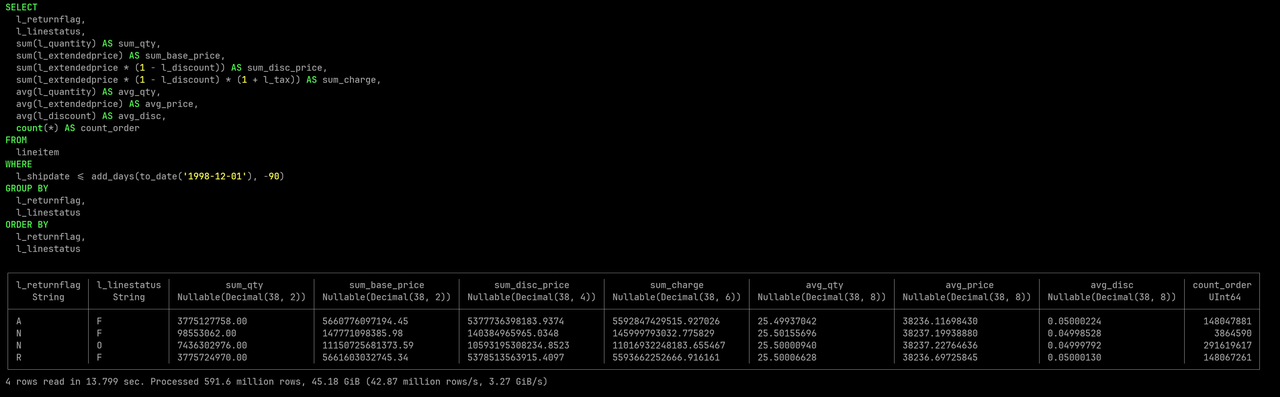
Databend 的算力可扩展性
作者:尚卓燃(PsiACE) 澳门科技大学在读硕士,Databend 研发工程师实习生 Apache OpenDAL(Incubating) Committer PsiACE (Chojan Shang) GitHub 对于大规模分布式数据处理系统,为了更好应对数据、流量、和复杂性的增长…...

「解析」Windows 如何优雅使用 Terminal
所谓工欲善其事必先利其器,对于开发人员 Linux可能是首选,但是在家学习的时候,我还是更喜欢使用 Windows系统,首先是稳定,其次是习惯了。当然了,我还有一台专门安装 Linux系统的小主机用于学习Linux使用&am…...
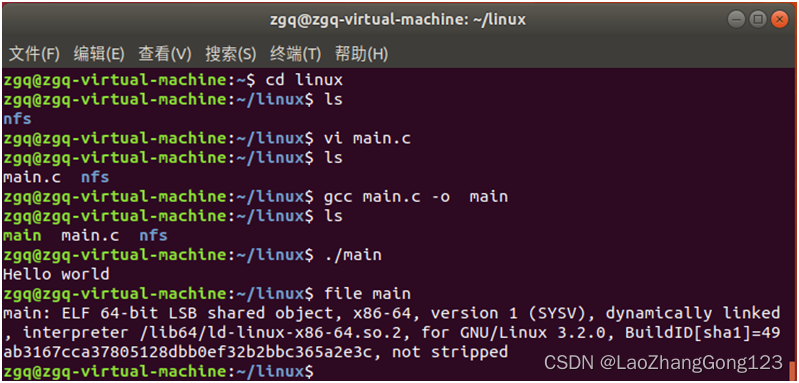
Linux第18步_安装“Ubuntu系统下的C语言编译器GCC”
Ubuntu系统没有提供C/C的编译环境,因此还需要手动安装build-essential软件包,它包含了 GNU 编辑器,GNU 调试器,和其他编译软件所必需的开发库和工具。本节用于重点介绍安装“Ubuntu系统下的C语言编译器GC&a…...

【Linux】Linux 基础命令 crontab命令
1.crontab命令 crond 是linux下用来周期性的执行某种任务或等待处理某些事件的一个守护进程,与windows下的计划任务类似,当安装完成操作系统后,默认会安装此服务 工具,并且会自动启动crond进程,crond进程每分钟会定期检查是否有要执行的任务,如果有要执行的任务,则自动…...
14:00面试,14:08就出来了,问的问题过于变态了。。。
从小厂出来,没想到在另一家公司又寄了。 到这家公司开始上班,加班是每天必不可少的,看在钱给的比较多的份上,就不太计较了。没想到10月一纸通知,所有人不准加班,加班费不仅没有了,薪资还要降40…...

Ubuntu envs setting
1. change the chmod of folders sudo chown -R $USER:$USER /home/anaconda3 2. torch.cuda.is_available()返回false change conda installation to pip. zai qi ta huan jing pei zhi dou mei wen ti de qing kuang xia , zai shi shi zhe ge fang fa. # CUDA 11.7 con…...
Windows 下用 C++ 调用 Python
文章目录 Part.I IntroductionChap.I InformationChap.II 预备知识 Part.II 语法Chap.I PyRun_SimpleStringChap.II C / Python 变量之间的相互转换 Part.III 实例Chap.I 文件内容Chap.II 基于 Visual Studio IDEChap.III 基于 cmakeChap.IV 运行结果 Part.IV 可能出现的问题Ch…...

九州金榜|家庭教育一招孩子不在任性
有一次和朋友一块聚餐,邻座是一位妈妈、和她大概七八岁的儿子,小男孩长得很帅气,没有像同龄人那样调皮捣乱,而是和妈妈很温馨的就餐。 看的出来一家人的素质很高,就餐过程中桌面保持的很整洁,交流声音也不…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
