编译原理笔记(三)
一、词法分析程序的设计
1、词法分析程序的输出
在识别出下一个单词同时验证其词法正确性之后,词法分析程序将结果以单词符号的形式发送至语法分析程序以回应其请求。
单词符号一般分下列5类:
- 关键字:如:begin、end、if、while和var。
- 标识符:如:常量名、变量名和过程名
- 常数:各种类型的常数,如:25、TRUE和"ABC"等。
- 运算符:如+、*、<、=等。
- 界符:如:逗号、分号、括号等、
2、词法分析程序中如何识别单词
常见的可以用于词法规则描述的工具有状态转换图、扩展巴克斯范式(EBNF)、有限状态自动机、正规表达式以及正规文法等。
二、单词的形式化描述工具
1、正规文法
正规文法也称3型文法G={VN,VT,S,P},其P中的每一条规则都有下述形式:A→aB或A→a,其中A,BVN,a
。正规文法描述的是VT上的正规集。
2、正规式
设字母表Σ={,
,|,.,*,(,)}。
1)ε和Ø都是Σ上的一个正规式,它们所表示的正规集为{ε}和Ø。
2)任何a∈Σ,a是Σ上的一个正规式,它所表示的正规集为{a}。
3)假设e1和e2是Σ上的正规式,它们所表示的正规集分别为L(e1)和L(e2),则
·e1|e2是Σ上的正规式,它所表示的正规集为L(e1|e2)= L(e1)∪L(e2)。
·e1e2是Σ上的正规式,它所表示的正规集为L(e1e2)= L(e1)L(e2)。
·(e1)*是Σ上的正规式,它所表示的正规集为L((e1)*)= L(e1)*。
4)仅由有限次上述3个步骤而定义的表达式才是Σ上的正规式,仅由这些正规式所表示的符号串的集合才是Σ上的正规集。
例子:令Σ={a,b},则有:
1)正规式a表示的正规集为{a}。
2)正规式a|b表示的正规集为{a,b}。3)正规式ab表示的正规集为{ab}。
4)正规式(a|b)(a|b)表示的正规集为{aa,ab,ba,bb}。
5)正规式a*表示的正规集为{ε,a,aa,aaa,…}。
6)正规式(a|b)*表示的正规集为{ε,a,b,aa,ab,ba,bb,aaa,…}。
7)正规式a|a*b表示的正规集为包含字符串a和包含0个或多个a后跟随一个b的所有的符号串。
若两个正规式e1和e2所表示的正规集相同,则说e1和e2等价,写作e1=e2。
设r,s,t为正规式,正规式服从的代数规律如下:
1)r|s=s|r
2)r|(s|r)=(r|s)|t
3)(rs)t=r(st)
4)r(s|t)=rs|rt,(s|t)r=sr|tr
5)r=r,r
=r
6)r|r=r
3、正规式转正规文法
字母表Σ上的正规式r到正规文法G-=(VN,VT,S,P)的转换方法为:
1)选择一个非终结符S生成类似产生式的形式:Sr,并将S定为G放识别符号。为表述方便,将S
r称作正规式产生式,因为在
右部中含有“.”,“*”或“|”等正规式符号,不是V中的符号。
2)若x和y都是正规式,对形如Axy的正规式产生式,重写成A
xB,B
y两个产生式,其中B是新选择的非终结符。
例:对于r=a(a|d)*
首先形成S
a(a|d)*,然后形成S
aA和A
(a|d)*,在形成
S
aA A
(a|d)B
A
B
{a|d)B
B
4、正规文法转正规式
| 文法产生式 | 正规式 | |
| 规则1 | A | A=xy |
| 规则2 | A | A=x*y |
| 规则3 | A | A=x|y |
例如:文法G[S]如下:
S
aA S
a A
aA A
dA A
a A
d
解:首先有
S=aA|a
A=(aA|dA)|(a|d)
再将A的正规式变换成A=(a|d)A|(a|d),又变换为A=(a|d)*(a|d),再代入S得:
S=a(a|d)*(a|d)|a
再利用正规式的代数变换可依此得到
S=a(a|d)*(a|d)|
S=a(a|d)*
三、有穷自动机
1、确定的有穷自动机
1.定义:一个确定的有限自动机(DFA) M是一个五元组:M=(K,Σ,f,S,Z),其中:
1)K是一个有限集,它的每一个元素称为一个状态。
2)Σ是一个有穷字母表,它的每个元素称为一个输入字符。
3)f是一个转换函数,是KΣ
K上的映像。
4)S∈K,是唯一的初态。
5)Z⊆S,F是一个终态集,可以为空。
2.DFA的状态转移矩阵
DFA可用一个二维矩阵表示,矩阵的行表示状态,列表示输入字符,矩阵元素表示δ(s,a)的值。
3.DFA是状态转换图
若设DFA M含有m个状态和n个输入字符,则这个图含有m个状态结点,每个结点至多有n条箭弧射出与其它的状态结点相连接,每个箭弧用Σ中的一个不同输入字符作为标记。整张图含有唯一的初态结点和若干终态结点。
例子:设DFA M=({0,1,2,3},{a,b},δ,{3}),其中,δ定义为:
δ(0,a)=1,δ(0,b)=2,δ(1,a)=3,δ(1,b)=2,δ(2,a)=1,δ(2,b)=3,δ(3,a)=3,δ(3,b)=3。
4.DFA的识别字符串
1)对Σ上的任何符号串w∈Σ*,若存在一条从初态结点到某一终态结点的通路,且该通路上所有弧的标记符连接成的字符串等于w,则称w可被DFA M所识别。若M的初态结点同时又是终态结点,则空字符串ε被M所识别。
2)DFA与语言的关系:DFA M所能识别的符号串的全体记为L(M)。
2、不确定的有穷自动机
1.定义:一个不确定有限自动机(NFA) M是一个五元组:M=(S,Σ,δ,S0,F),其中:
1)S是一个有限集,它的每一个元素称为一个状态。
2)Σ是一个有穷字母表,它的每个元素称为一个输入字符。
3)δ是一个从S×Σ到S的子集的映射,即δ:S×Σ*→2S
4)S0⊆S,S0是一个非空初态集。
5)F ⊆S,F是一个终态集,可以为空。
2.NFA的状态转换图
若设NFA M含有n个状态和m个输入符号,则这个图含有n个状态结点,每个结点可射出若干箭弧与其它的状态结点相连接。对于w∈{ε}∪Σ,若δ(q0,a)={q1,q2,…,qk}(k≥0),则从q0出发,分别到q1,q2,…,qk的k条弧,弧上均标记为a。整张图含有唯一的初态结点和若干终态结点。
3.NFA识别字符串
1)对Σ*上的任何符号串,若存在一条从某一初态结点到某一终态结点的通路,且该通路上所有弧的标记符号依次连接成的字符串等于w,则称w可被NFA M所识别。若M的某些结点同时又是终态结点,则空字符串ε被M所识别。
2)NFA与语言的关系:Σ*中所有可被NFA M所识别的符号串的集合记为L(M)。
4.DFA和NFA的关系
1)DFA是NFA的特例,NFA是DFA概念的推广。
2)NFA能识别的语言都能被一个DFA识别。
3)DFA相对NFA的识别程序更容易实现。
3、NFA转换为等价的DFA
1.NFA的确定化:对任给的NFA M。都能相应地构造一个DFA M‘,使得L(M’)=L(M)。
2.NFA的子集法:DFA的每一个状态代表NFA状态集合的某个子集,构造的DFA使用它的状态去记录NFA读入输入符号之后可能到达的所有状态的集合。
3.状态集合I的a弧转换,表示为ε-Closure(I),定义为一个状态集,是状态集I中的一组任何状态S经任意条ε弧而能够到达的状态的集合。
4.状态集合I的a弧转换,表示为move(I,a),定义为状态集合J,其中J是所有那些可以从I中的某一状态经过一条a弧而到达的状态的全体。
4、确定有限自动机的化简
1.化简的目的:去除多余或等价的状态,降低存储代价,提高句子识别的效率。
2.有限自动机的多余状态:从初态出发,任何可识别的输入串也不能到达的状态。
3.状态等价:在两个状态s和t等价的条件是以下两个:
一致性条件--状态s和t必须同时为可接受状态或不可接受状态。
蔓延性条件--对于所有输入符号,状态s和状态t必须转换到等价的状态里。
4.DFA的化简(分割法):
i)将DFA M的状态集S划分为两个子集;终态集F和非终态集F ̃,形成初始划分Π。
ii)对Π建立新的划分Πnew。对Π中的每个状态子集G进行如下变换:
a)把G划分成新的子集,使G的两个状态s和t属于同一个子集,当且仅当对任何输入符号a,状态s和t转换到的状态都属于Π的同一子集。
b)用G划分出的所有新子集替换G,形成新的划分Πnew。
iii)若Πnew和Π相等,则执行第iv)步,否则,令Π=Πnew,重复第ii)步。
iv)划分结束后,对划分中的每个状态子集,选出一个状态作为代表,删去其它一切等价的状态,并把射向其它状态的箭弧改为射向这个代表的状态。
四、正规式与有限自动机之间的等价性
1.由正规式构造有限自动机
消去结点的规则如下:
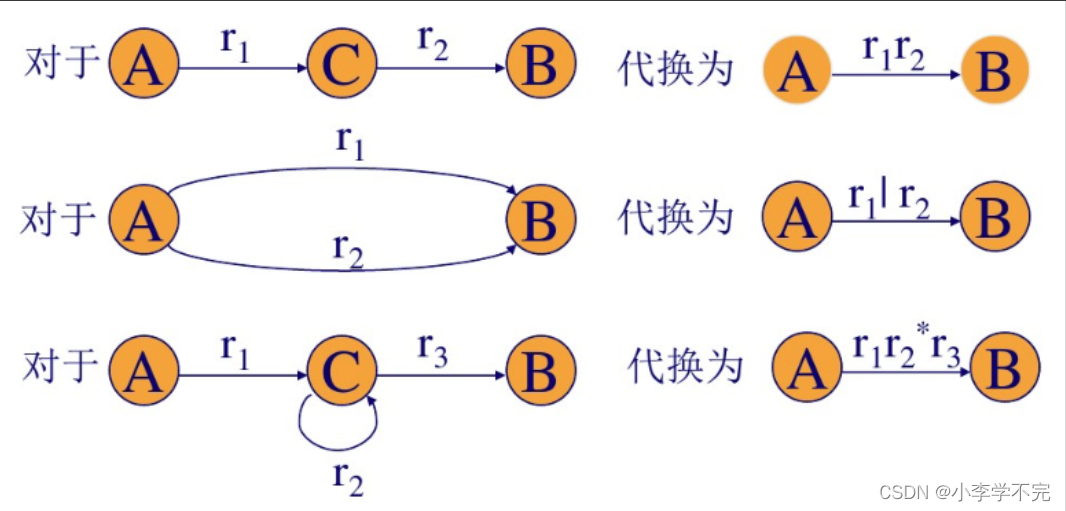
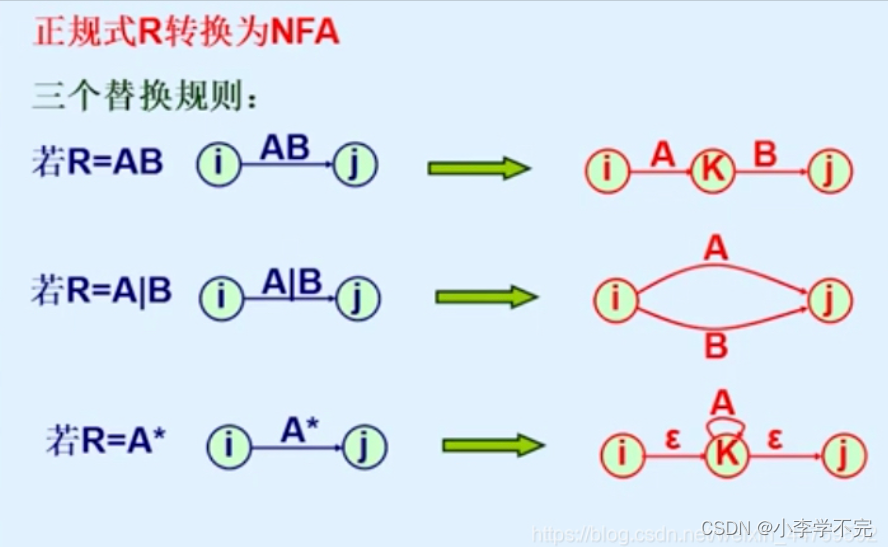
相关文章:

编译原理笔记(三)
一、词法分析程序的设计 1、词法分析程序的输出 在识别出下一个单词同时验证其词法正确性之后,词法分析程序将结果以单词符号的形式发送至语法分析程序以回应其请求。 单词符号一般分下列5类: 关键字:如:begin、end、if、whil…...

DDoS攻击的多种方式
DDOS攻击指分布式拒绝服务攻击,即处于不同位置的多个攻击者同时向一个或数个目标发动攻击,或者一个攻击者控制了位于不同位置的多台机器并利用这些机器对受害者同时实施攻击。由于攻击的发出点是分布在不同地方的,这类攻击称为分布式拒绝服务…...

SpringValidation自定义注解以及分组校验
SpringValidation的参数校验使用可参考:【SpringMVC应用篇】Spring Validation 参数校验-CSDN博客 目录 1. 引入依赖 2. 自定义注解校验 2.1 创建Validation类 2.2 创建注解对象 2.3 使用注解 3. 分组校验 3.1 实体类内部定义接口 3.2 在参数上指定分组 1. …...

Multisim各版本安装指南
Multisim下载链接 https://pan.baidu.com/s/1En9uUKafhGOqo57V5rY9dA?pwd0531 1.鼠标右击【Multisim 14.3(64bit)】压缩包(win11及以上统需先点击“显示更多选项”)选择【解压到 Multisim 14.3(64bit)】。 2.打开解压后的文件夹,双击打开【…...
大学生搜题软件,未来可期吗?
作为一家专注于软件开发的公司《智创有术》,我们致力于为客户提供创新、高效和可靠的解决方案。通过多年的经验和专业知识,我们已经在行业内建立了良好的声誉,并赢得了客户的信任和支持。 支持各种源码,网站搭建,APP&a…...
JMeter使用
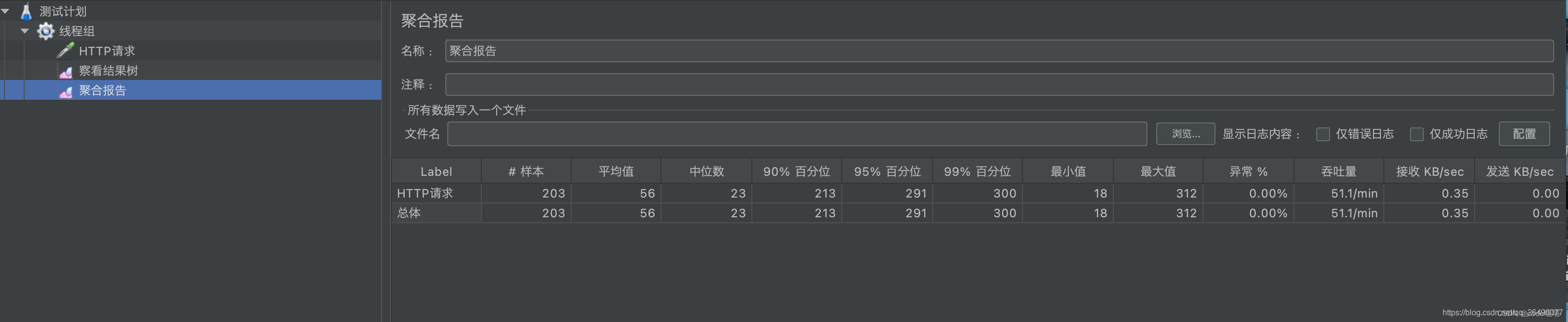
目录 启动JMeter 创建线程组 设置线程参数 设置http请求参数 编辑 创建查看结果树(显示成功/失败多少以及返回结果等信息) 创建聚合报告(显示响应时间、吞吐量、异常数等信息) 点击上方的执行按钮即可开始压力测试 结果树显示 聚合报告结果显示 启动JMeter 在JMete…...
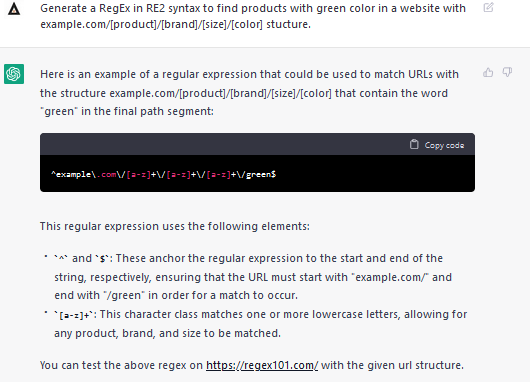
ChatGPT 进行 SEO的使用技巧
搜索引擎优化 (SEO) 是使网站对搜索引擎友好的一种不断发展的实践。 自搜索引擎和新兴技术的发展以来,它从未保持不变。 最近发布的 ChatGPT 是一种人工智能对话工具,似乎在搜索引擎优化方面有很好的应用。 从创建吸引人的标题到只需一个简短的提示就可…...
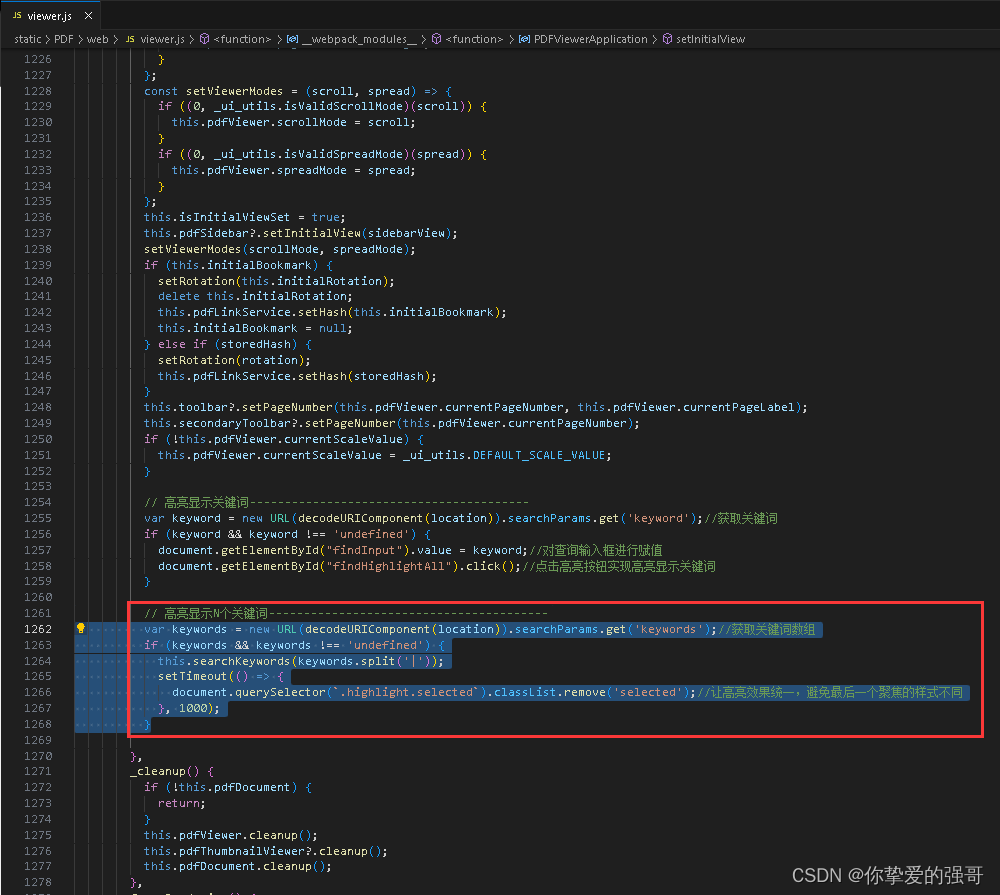
PDF.js实现搜索多个不同的关键词高亮显示效果
static\PDF\web\viewer.js 392行左右 // 自定义搜索关键词---------------------------------------- this.searchKeywords = keyword => {if (typeof PDFViewerApplication !== undefined) {PDFViewerApplication.eventBus.dispatch(find, {query: keyword,caseSensitive:…...

ES高级用法:DeleteByQueryRequest
背景 在Elasticsearch中,delete_by_query API 允许你基于查询条件删除文档。在Java中,你可以使用Elasticsearch的Rest High Level Client或者Transport Client来执行这个操作。 示例代码 下面是使用Rest High Level Client进行delete_by_query操作的一…...
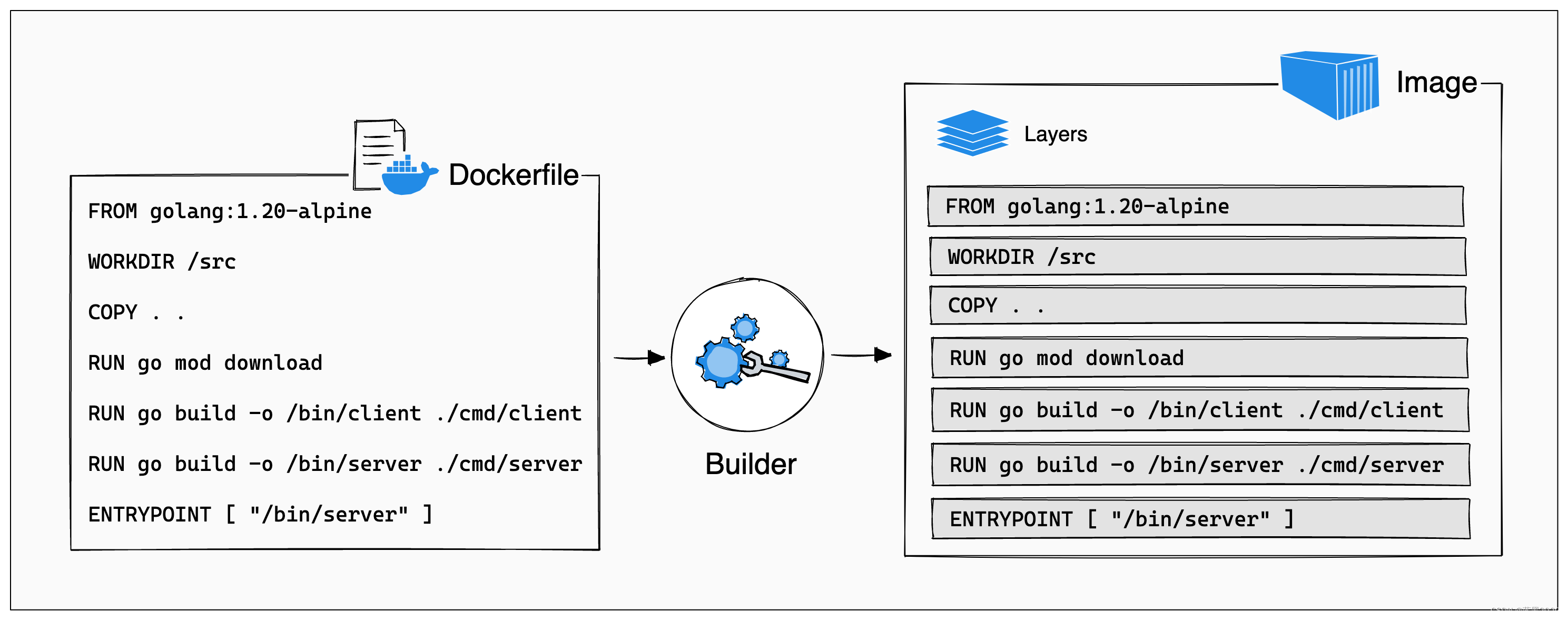
使用docker build构建image
文章目录 环境步骤准备例1:基本用法例2:缓存layer例3:Multi-stage例4:Mountcache mountbind mount 例5:参数例6:Export文件例7:测试 参考 环境 RHEL 9.3Docker Community 24.0.7 步骤 在Dock…...
【亲测有效】Win11 卸载MySQL5.7以及安装MySQL8.0.35
目录 一、卸载原来本地的mysql5.7 1.mysql服务部分 1.1停止mysql服务 1.2删除mysql服务 2.卸载 MySQL程序 3.残余文件的清理 3.1删除mysql安装的目录 3.2删除mysql数据存放的目录 3.3删除mysql自定义目录 4.清理注册表 5.删除环境变量配置 二、安装mysql8.0.35 1.…...

Beauty algorithm(三)腮红
查阅资料了解到腮红位于苹果肌处,同样使用关键点确定目标区域,然后对该区域进行渲染达到美妆效果。考虑到如果使用简单的RGB是很难做到特效,本篇采用模板方式进行区域融合。 一、skills 前瞻 1、png图像读取 cv::imread(imgPath, cv::IMREAD_UNCHANGED) IMREAD_UNCHANGE…...
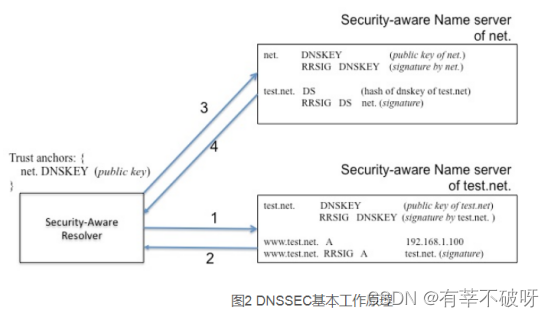
DNS安全与访问控制
一、DNS安全 1、DNSSEC原理 DNSSEC依靠数字签名保证DNS应答报文的真实性和完整性。权威域名服务器用自己的私有密钥对资源记录(Resource Record, RR)进行签名,解析服务器用权威服务器的公开密钥对收到的应答信息进行验证。如果验证失败&…...

【LMM 011】MiniGPT-5:通过 Generative Vokens 进行交错视觉语言生成的多模态大模型
论文标题:MiniGPT-5: Interleaved Vision-and-Language Generation via Generative Vokens 论文作者:Kaizhi Zheng* , Xuehai He* , Xin Eric Wang 作者单位:University of California, Santa Cruz 论文原文:https://arxiv.org/ab…...
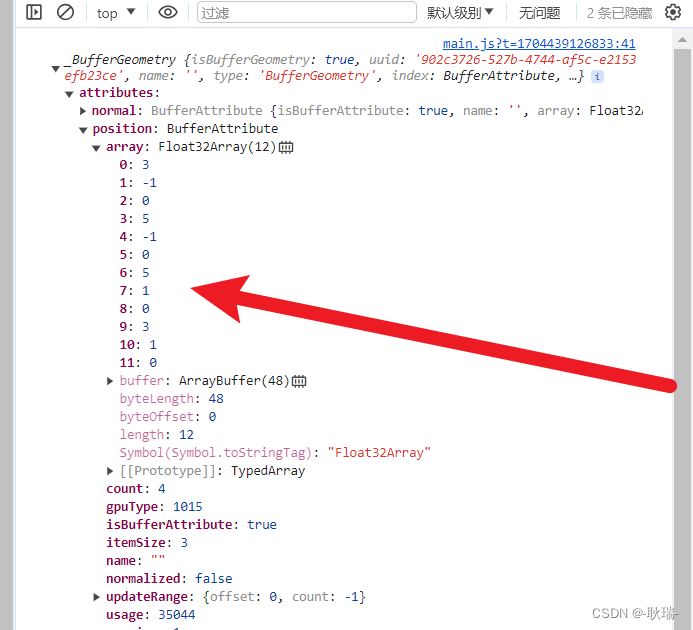
WEB 3D技术 three.js 顶点交换
本文 我们来说 顶点的转换 其实就是 我们所有顶点的位置发生转变 我们整个物体的位置也会随之转变 这里 我们编写代码如下 import ./style.css import * as THREE from "three"; import { OrbitControls } from "three/examples/jsm/controls/OrbitControls.j…...

ROS学习笔记(11)进一步深入了解ROS第五步
0.前提 我在学习宾夕的ROS公开课的时候发现,外国的对计算机的教育和国内的是完全不一样的,当你接触了外国的课程后回头看自己学的会发现好像自己啥也没学。我这里可以放出来给大家看一下。 1.Python and C 2.Python PDB Tutorial:Python Deb…...
性能优化-OpenMP基础教程(四)-Android上运行OpenMP
本文主要介绍如何在一个常规的Android手机上调试OpenMP程序,包括Android NDK的环境配置和使用JNI编写一个OpenMP程序运行在Android手机中。 🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:高性能&#…...
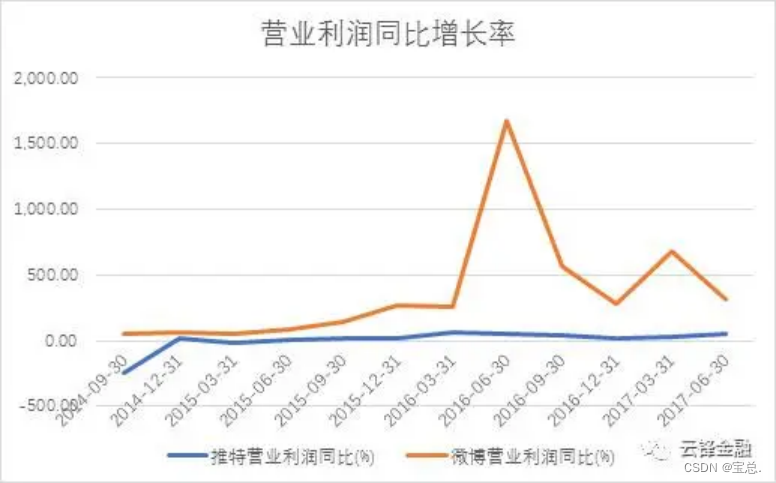
【转载】-财报-丈母娘教咱看财报(资产负债表-利润表-现金流量表)
写在前面 近期,在知乎看到“云峰金融”的一篇关于金融知识的文章《丈母娘教你看财报》,挺有意思的,挑出核心内容,又添加了一些内容的解释,特来分享一下。对于金融入门小白来讲,非常友好。如有不正确的地方&…...

HTML5大作业-精致版个人博客空间模板源码
文章目录 1.设计来源1.1 博客主页界面1.2 博主信息界面1.3 我的文章界面1.4 我的相册界面1.5 我的工具界面1.6 我的源码界面1.7 我的日记界面1.8 我的留言板界面1.9 联系博主界面 2.演示效果和结构及源码2.1 效果演示2.2 目录结构2.3 源代码 源码下载 作者:xcLeigh …...

数字IC后端设计实现之Innovus update_names和changeInstName的各种应用场景
今天吾爱IC社区小编给大家分享下数字IC后端设计实现innovus中关于update_names和changeInstName在PR中的具体使用方法。 update_names 1)为了避免和verilog语法保留的一些关键词,比如input,output这些,是不允许存在叫这类名字的…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

