数据结构:树详解
创建二叉树
给出了完整的先序遍历序列,子树为空用’#’表示,所以这样我们在通过先序遍历序列创建二叉树时我们直到先序遍历序列是先进行根结点,然后左子树最后右子树的顺序进行遍历的,所以对于完整的先序遍历序列我们可以直到先序遍历序列中第一个元素是二叉树的根结点,如果第二个元素不为’#’,那么这个代表二叉树有左孩子,而且左孩子的值为先序遍历序列的第二个元素的值,依次类推,根据二叉树的完整先序遍历序列我们可以直到每一个结点是否为空,这样我们就能够采取递归形式进行二叉树的创建:
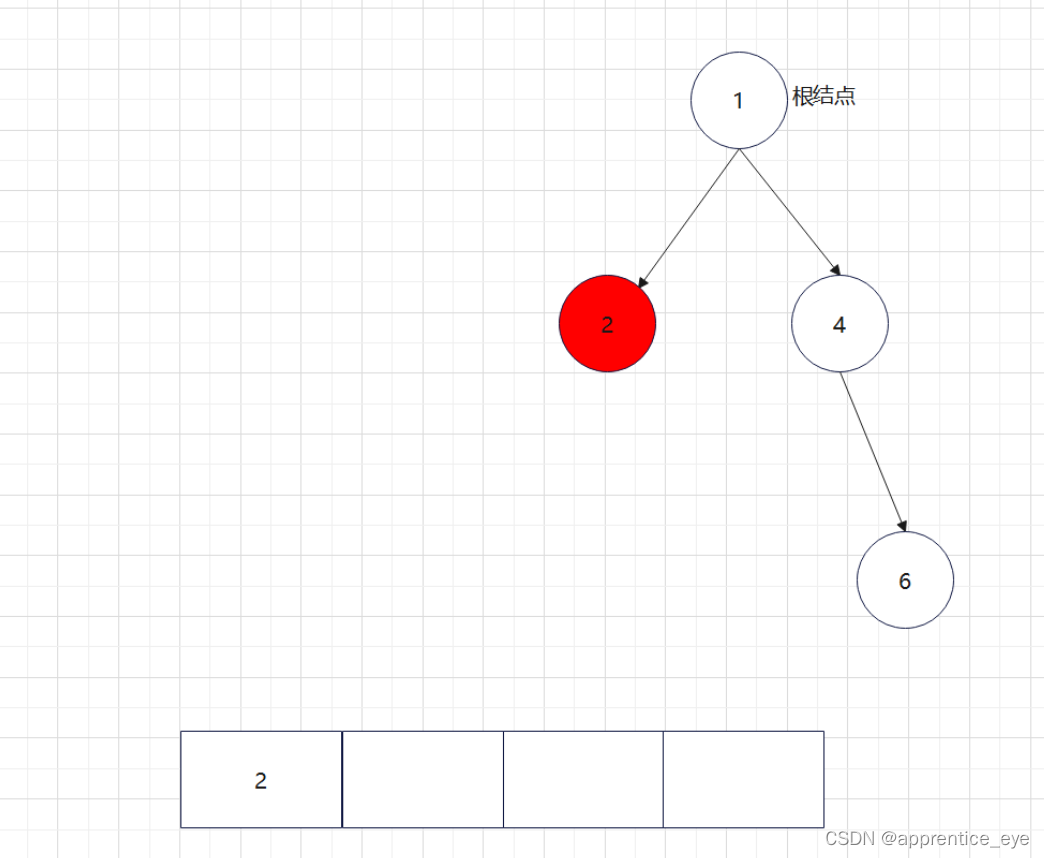
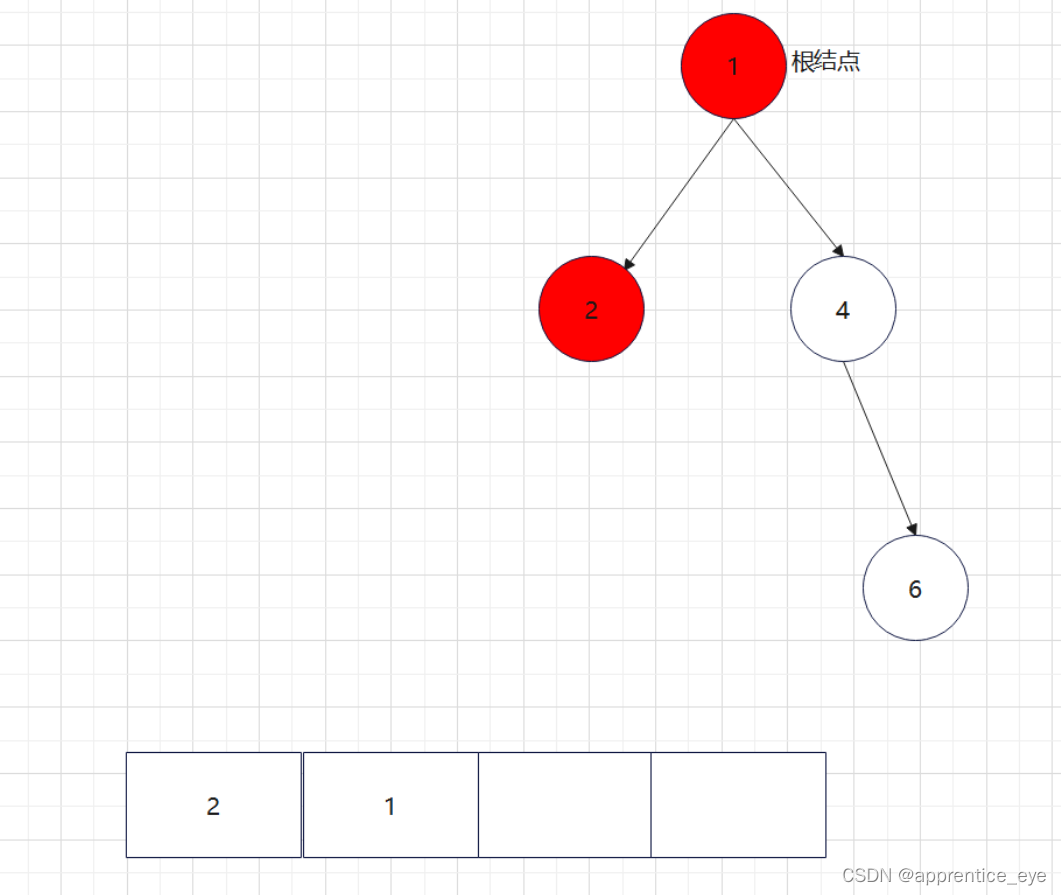
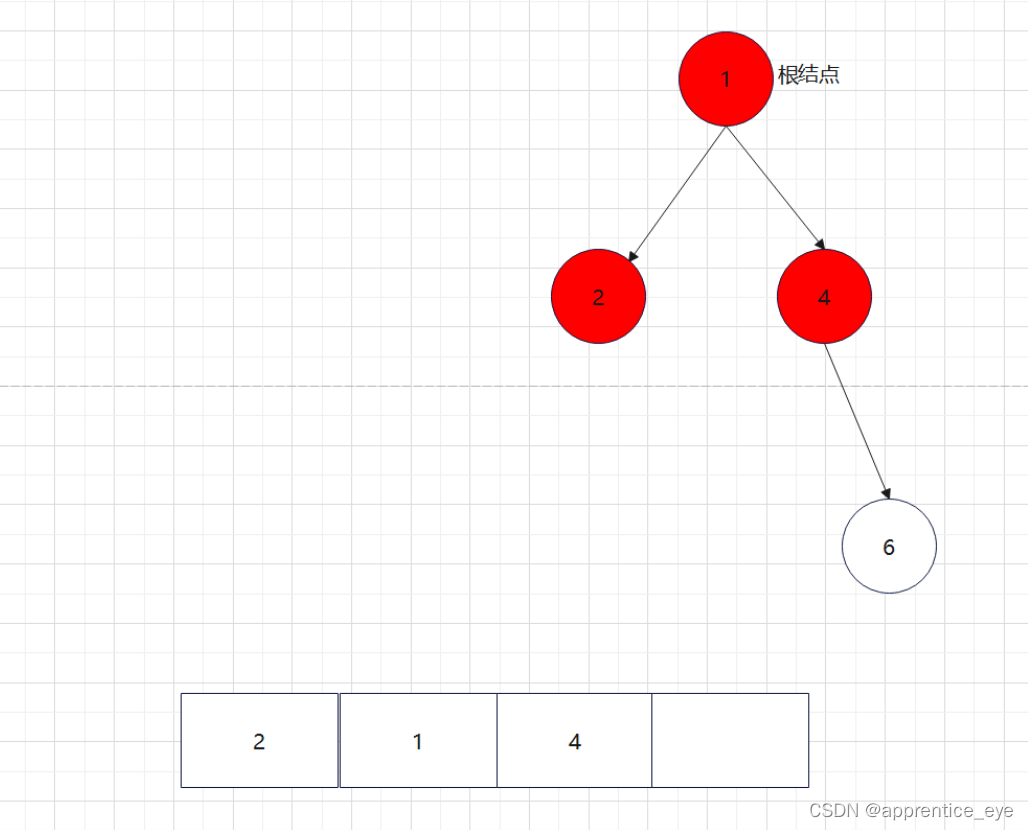
创建过程的图示为如下:
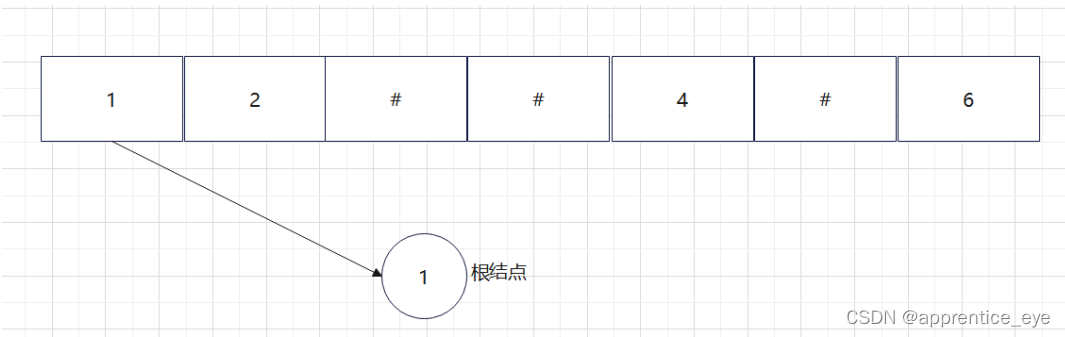
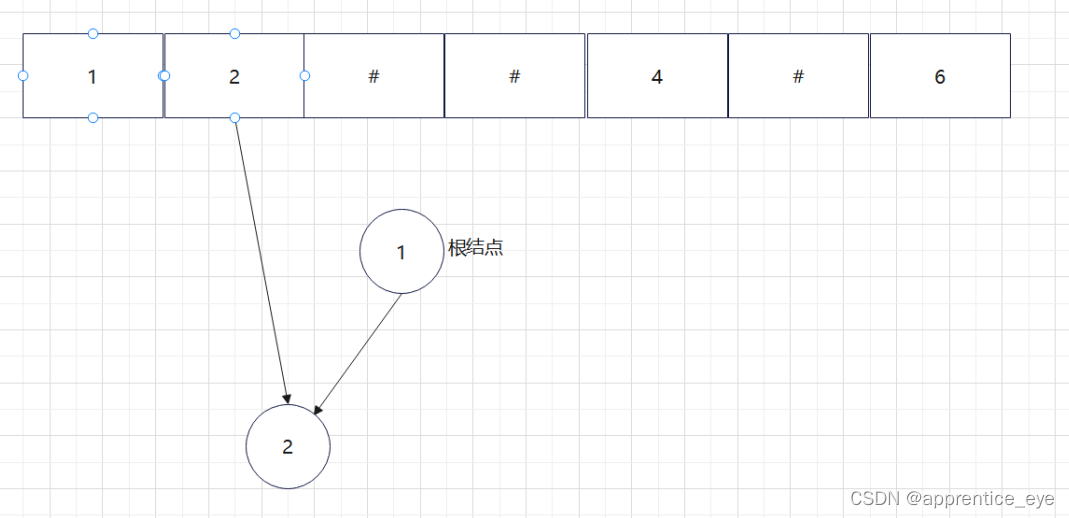
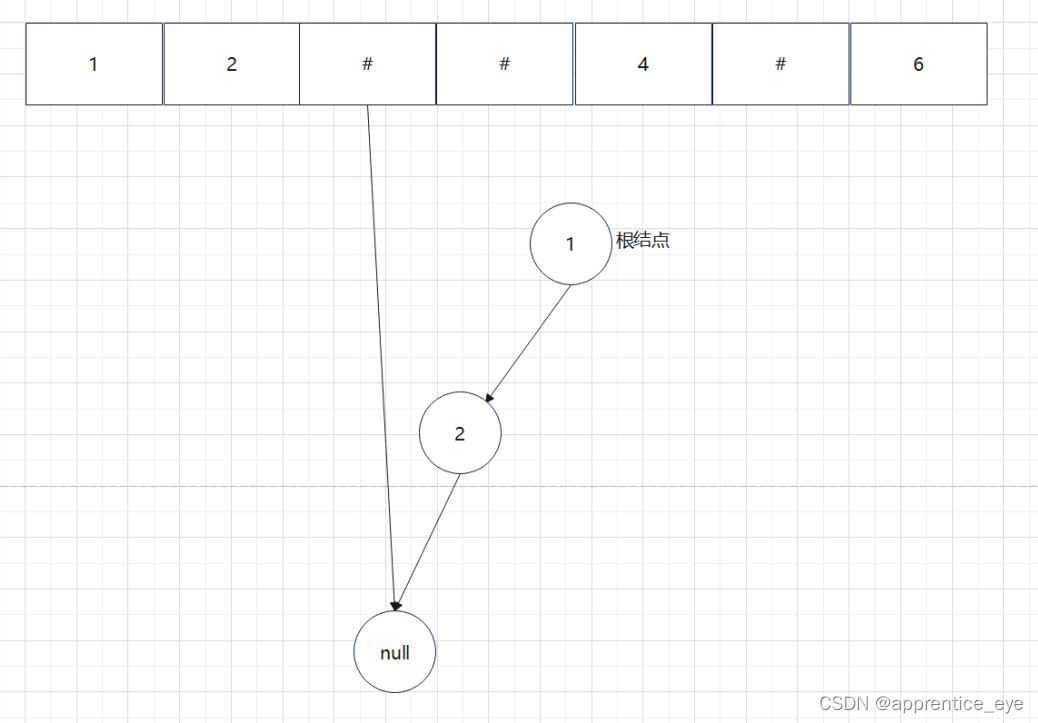
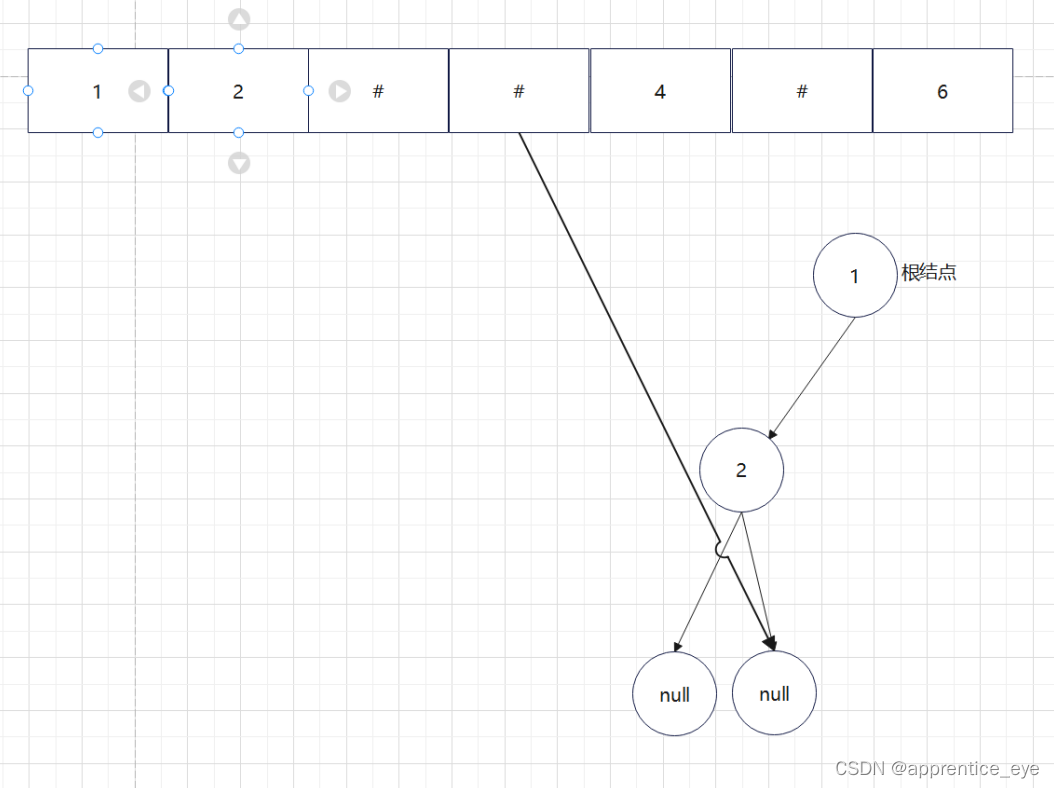
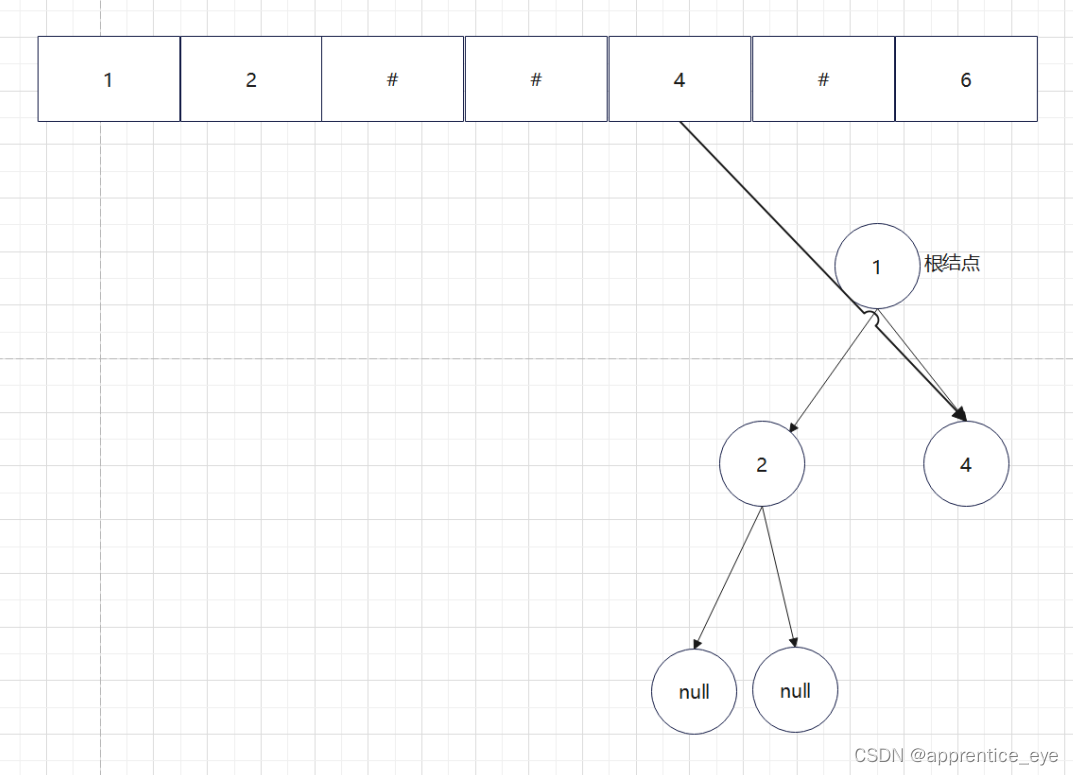
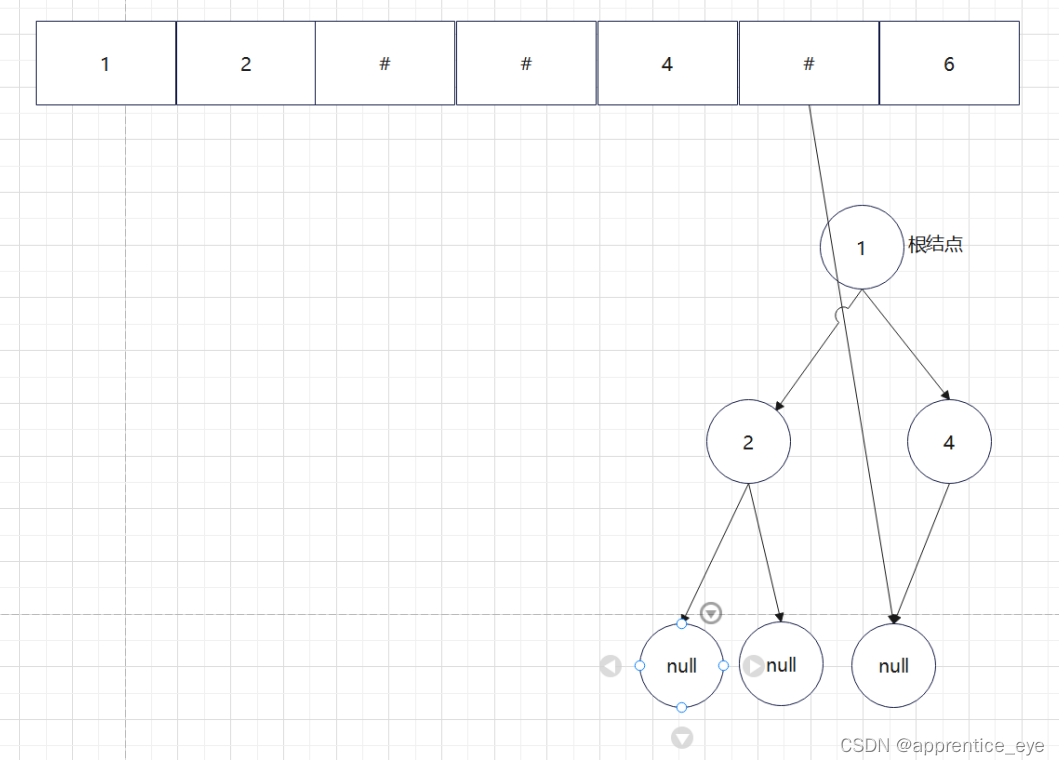
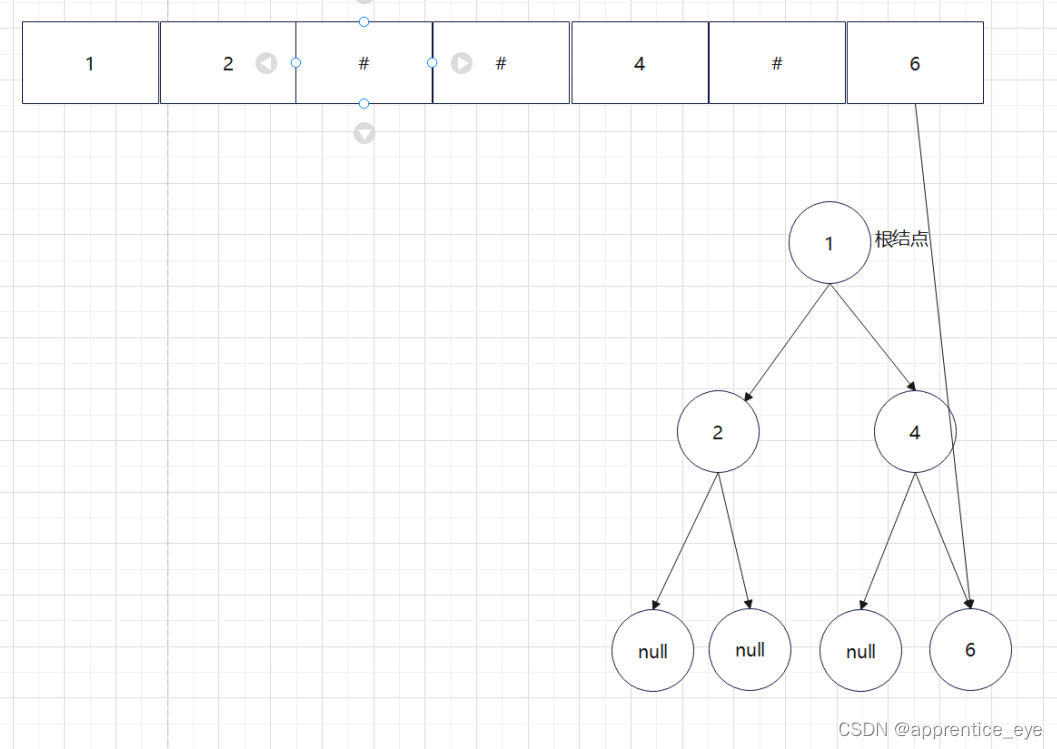
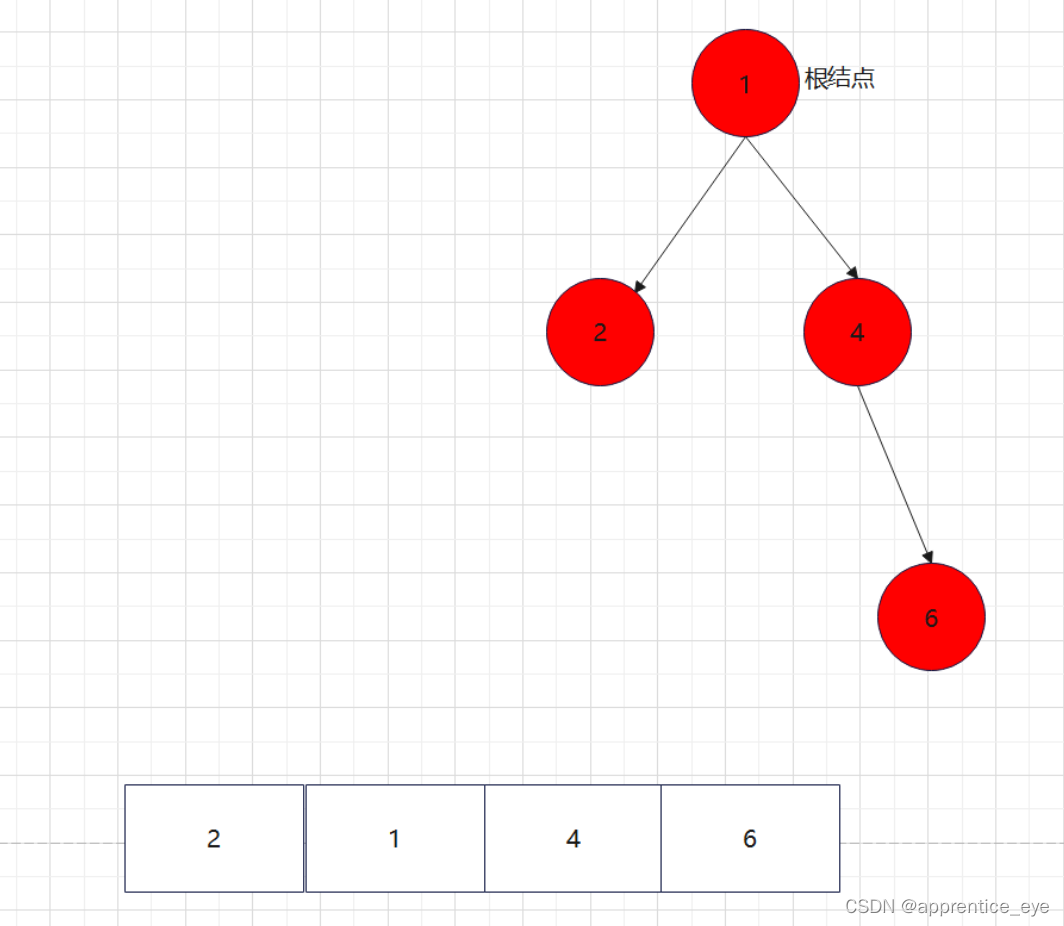
最终我们得到的树如下图所示:
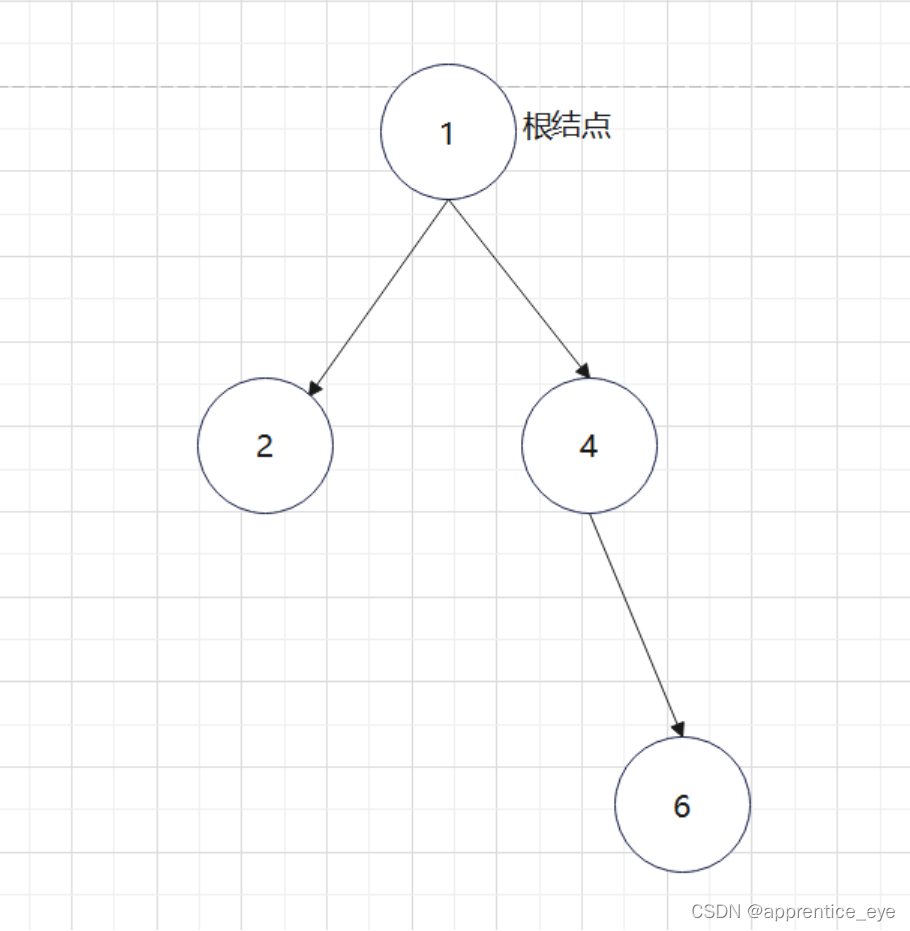
有了上面的思路我们可以写出如下代码:
void InitBinaryTree(char *p, int *length, struct BinaryTreeNode **root){if(p[*length]!=0){if(p[*length]!='#'){*root = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));(*root)->val = p[*length];(*root)->left = NULL;(*root)->right = NULL;(*length)++;InitBinaryTree(p, length, &(*root)->left);InitBinaryTree(p, length, &(*root)->right); }else{(*length)++;}}
}
这就是通过树的完整前序遍历序列创建二叉树的过程。
下面我们来进行实现二叉树的前序遍历、中序遍历与后序遍历,前序遍历是指先根结点再左子树最后右子树,中序遍历是先左子树然后根结点最后右子树,后序遍历是先左子树然后右子树最后根结点,这种遍历可以通过递归进行实现,在每次递归中所在结点不为NULL就说明结点有值,我们需要遍历这一个结点的左子树与右子树,也就是递归截至的条件是root==NULL;有了这样的思路前序遍历与中序遍历,与后序遍历就只是根结点的访问顺序发生改变,我们可以写出下面的三种遍历的代码:
前序遍历:
//本函数实现二叉树的前序遍历功能
void preOrderTraversal(struct BinaryTreeNode *root){if(root!=NULL){printf("%c ", root->val);preOrderTraversal(root->left);preOrderTraversal(root->right); }
}
中序遍历:
//本函数实现二叉树的中序遍历功能
void inOrderTraversal(struct BinaryTreeNode *root){if(root!=NULL){inOrderTraversal(root->left);printf("%c ", root->val);inOrderTraversal(root->right); }
}
后序遍历:
// 本函数实现二叉树的后序遍历功能
void postOrderTraversal(struct BinaryTreeNode *root){if(root!=NULL){postOrderTraversal(root->left);postOrderTraversal(root->right);printf("%c ", root->val); }
}
就以上面的建立的二叉树为例查看一下该二叉树的前序遍历序列、中序遍历序列、后序遍历序列。
二叉树的前序遍历序列应为:
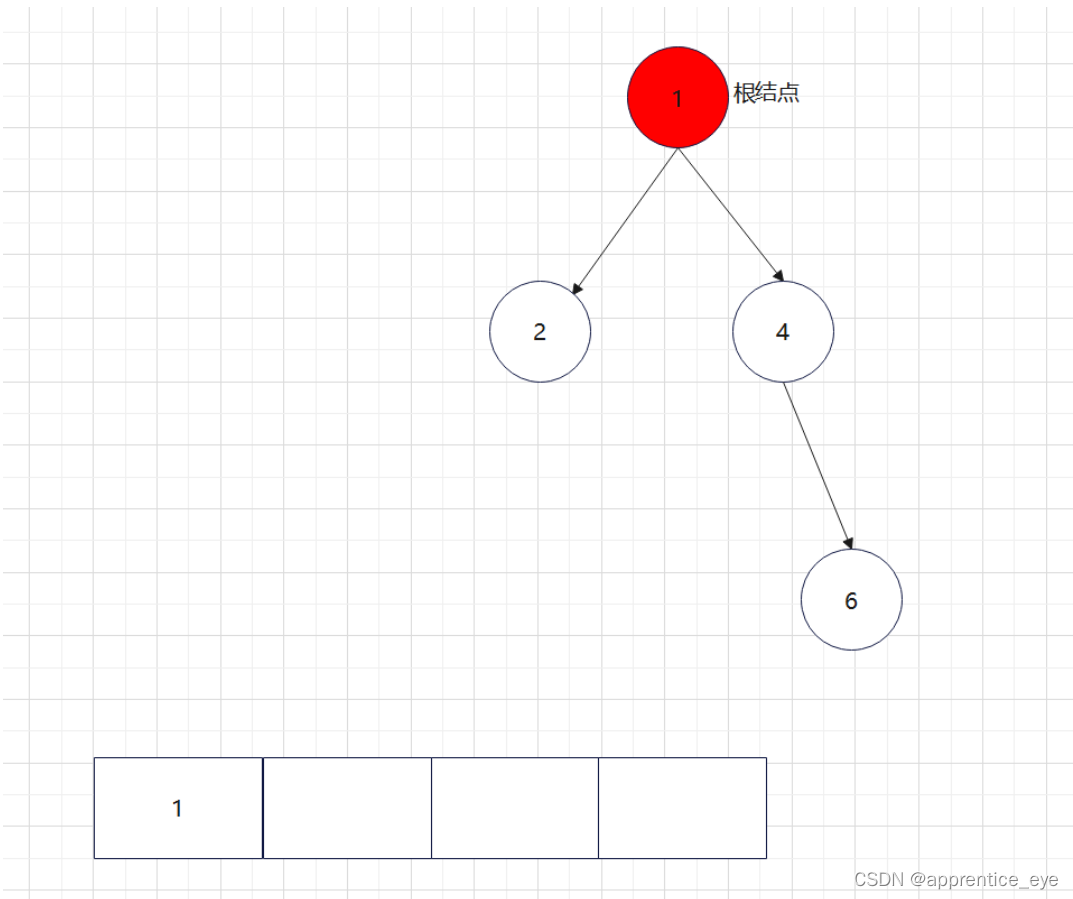
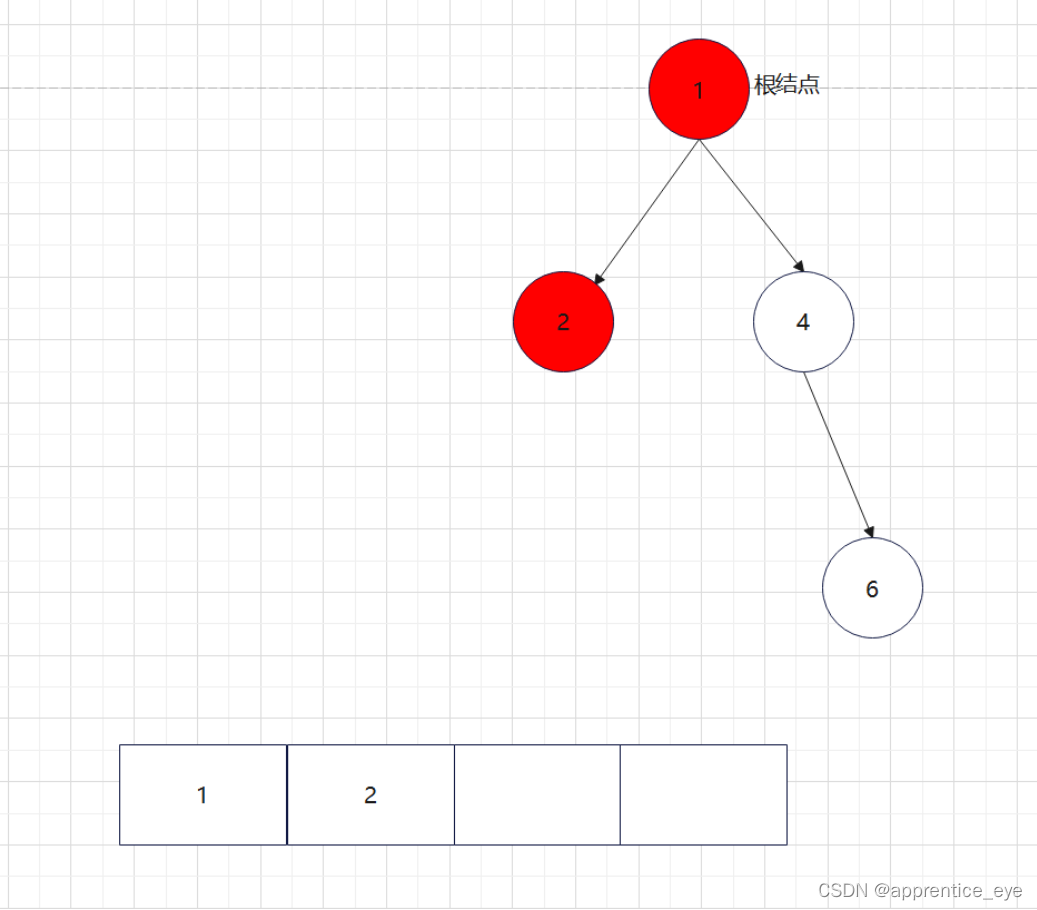
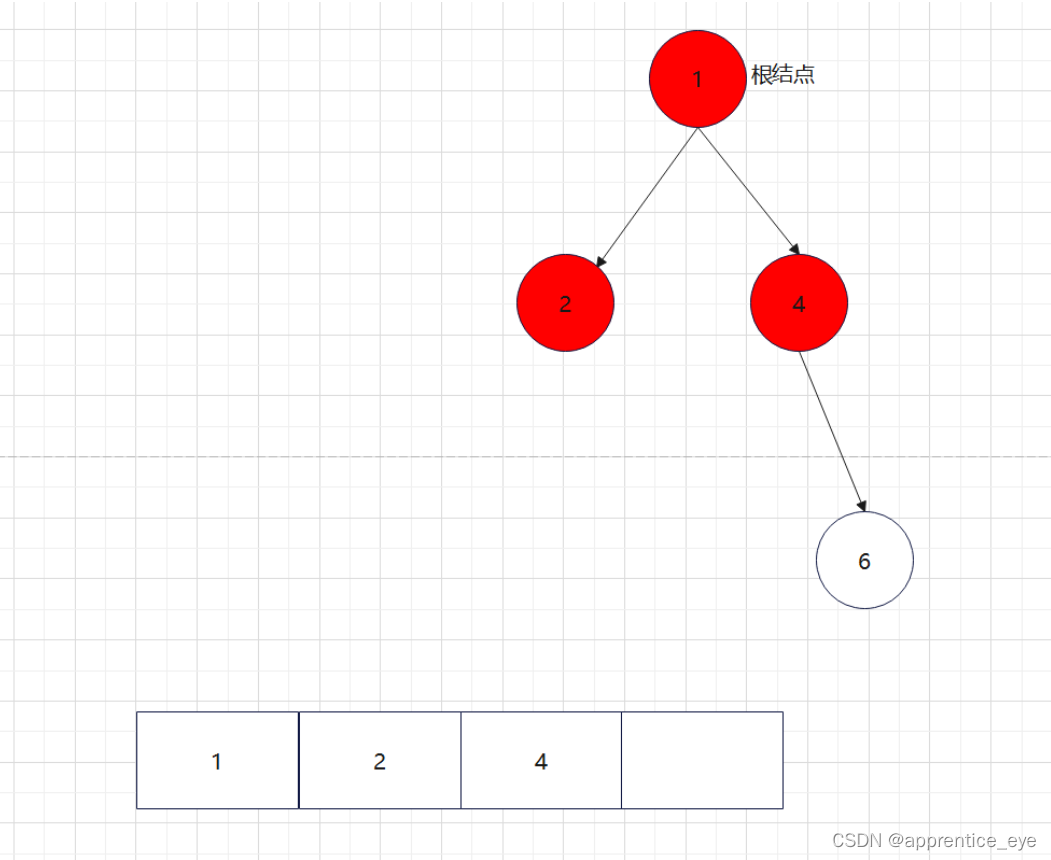
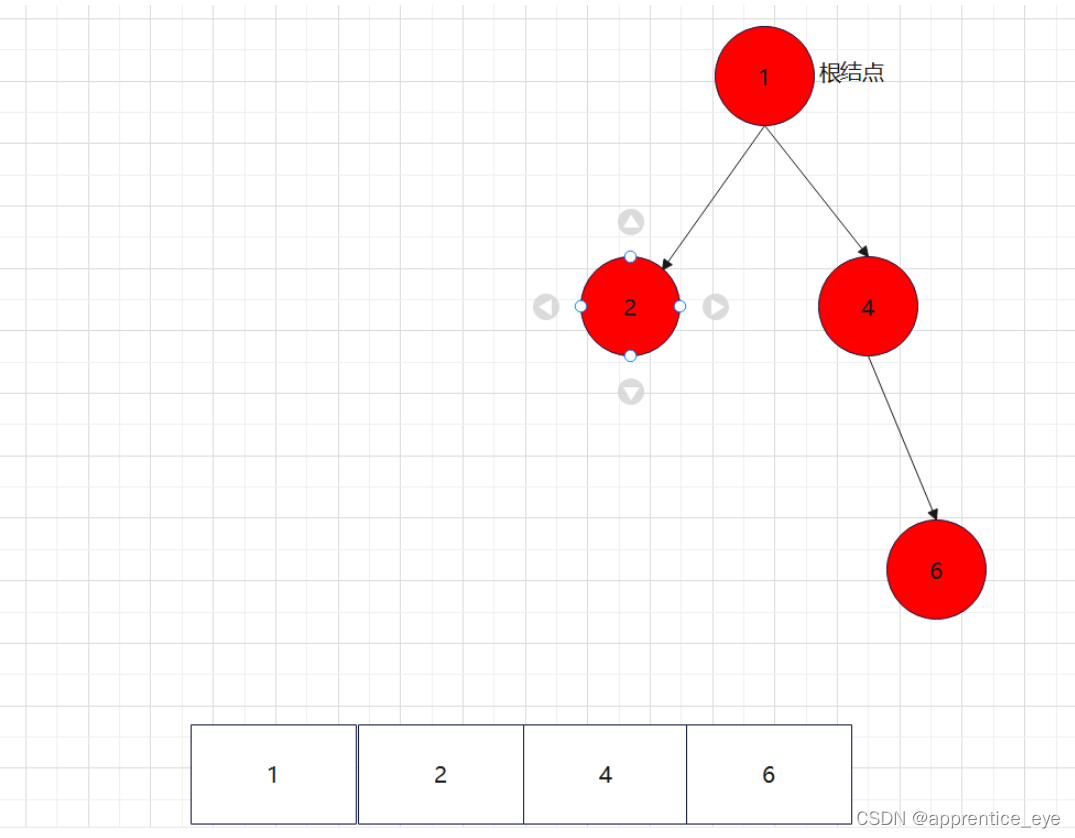
中序遍历序列应为:
后序遍历序列应为:
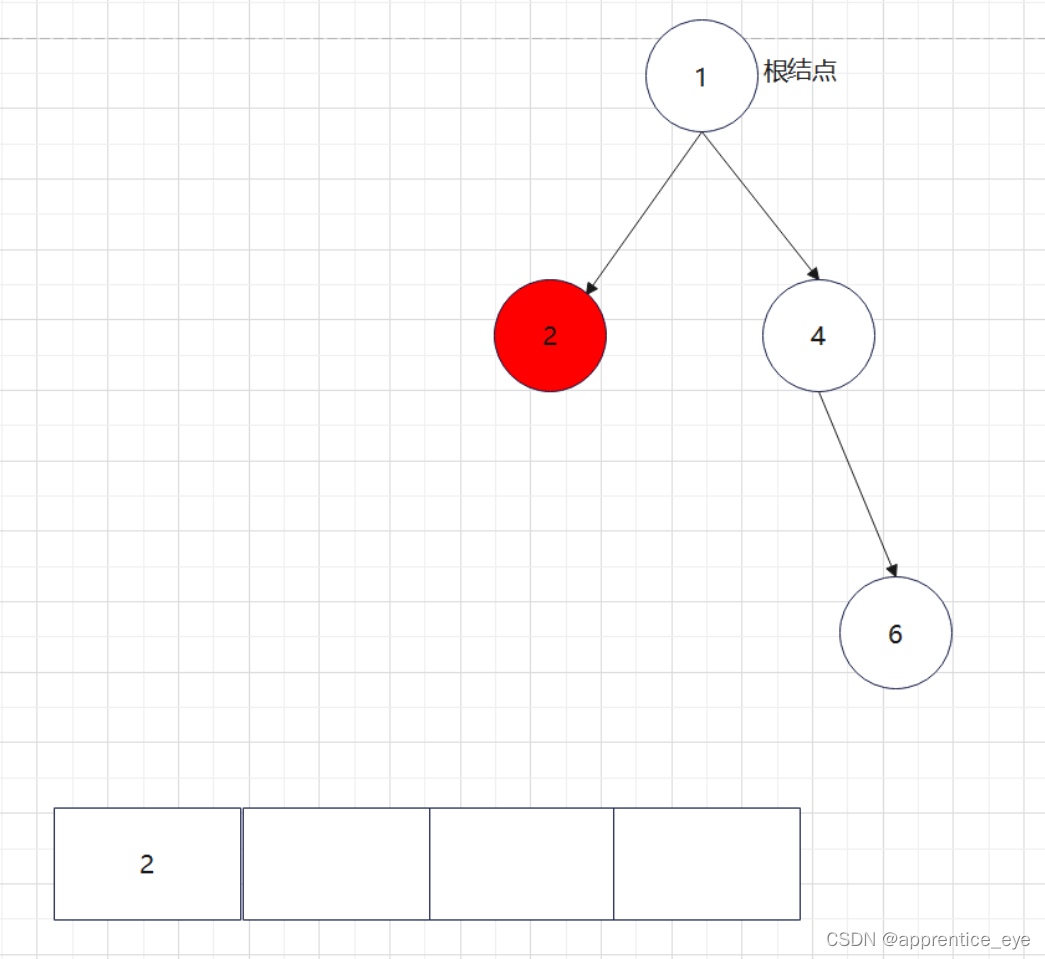
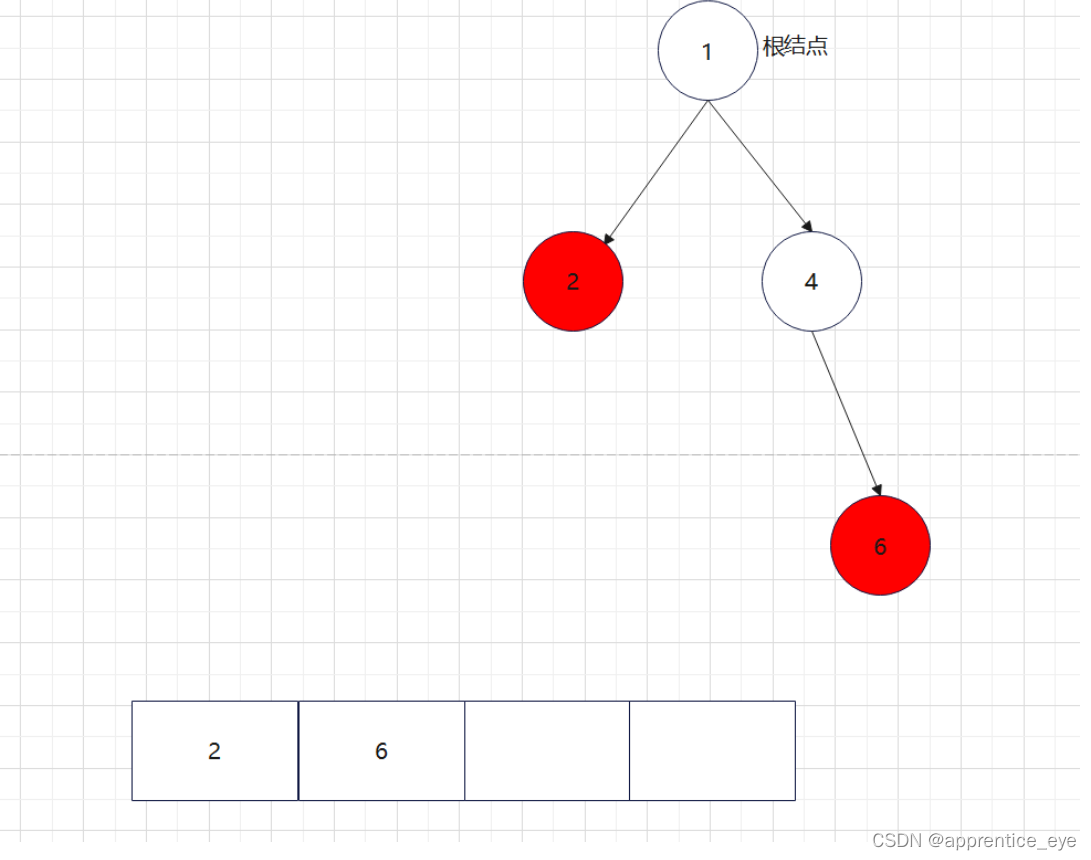
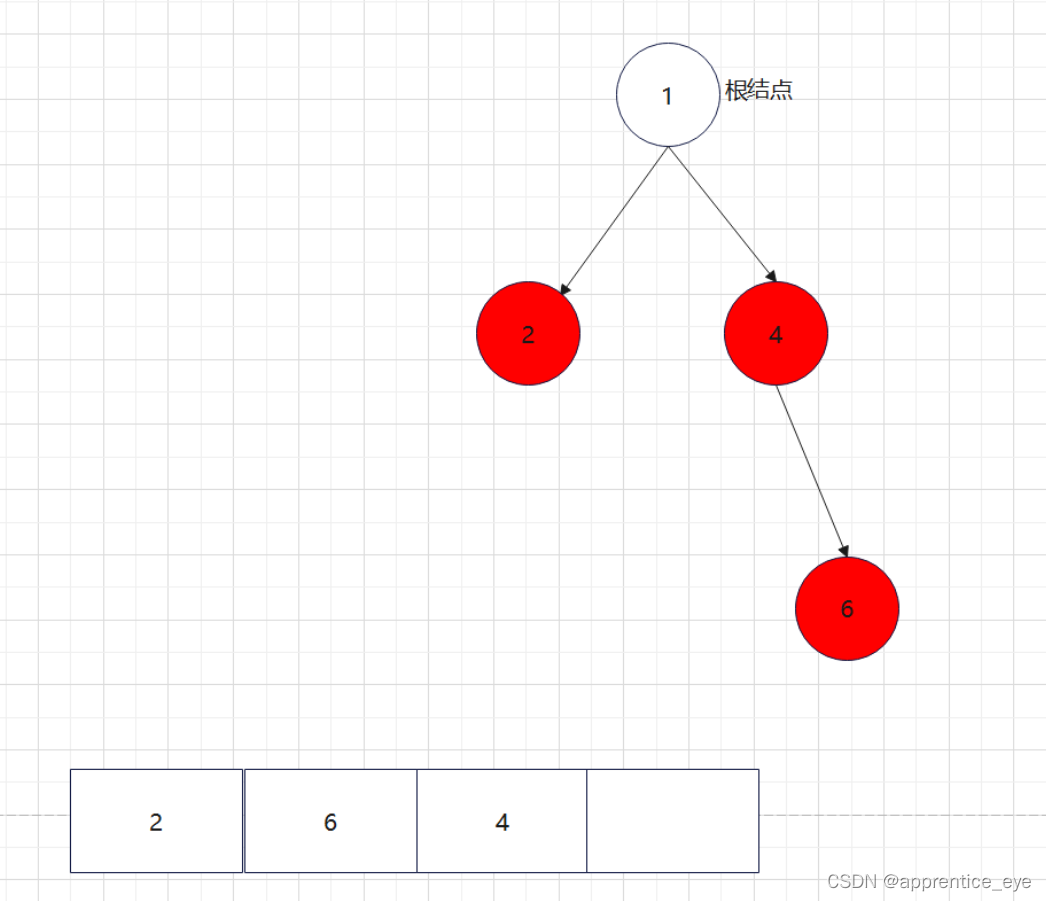
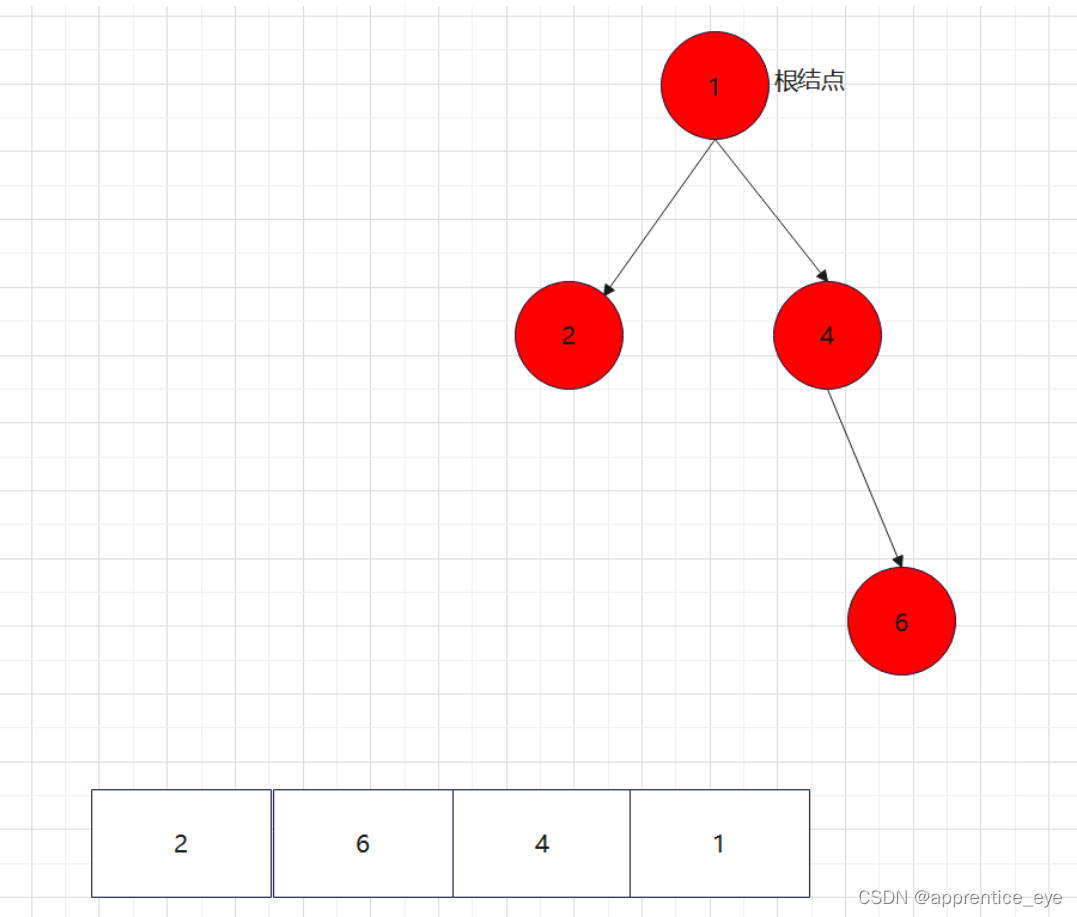
我们来运行一下看看结果是否正确:
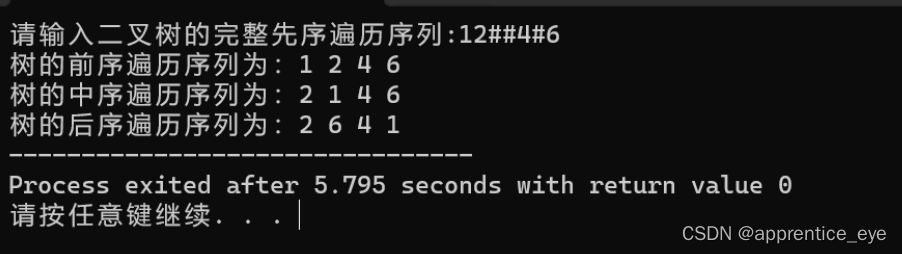
可以看出结果确实正确。
至此关于二叉树的内容已经全部实现,接下来实现哈夫曼树以及编码操作,题目中给出了’a’ ‘b’ ‘c’ ‘d’以及其对应出现的次数分别是7、5、2、4,出现次数多的字母编码要尽可能的短,我们可以利用哈夫曼树来实现对应的操作,哈夫曼树是为每个结点增加一个权值,权值大的结点离根要尽可能的近,我们就可以将所有的字符视作只有一个根结点的树,将结点权值小的两个子树进行合成组成一颗新树,两个子树的权值之和作为新树的权值,这一颗新树与剩余的所有树组成一个新的集合,然后从中选取两个树进行上述过程,如此重复下去,直到剩下一棵树,这棵树就是哈夫曼树。图示如下:

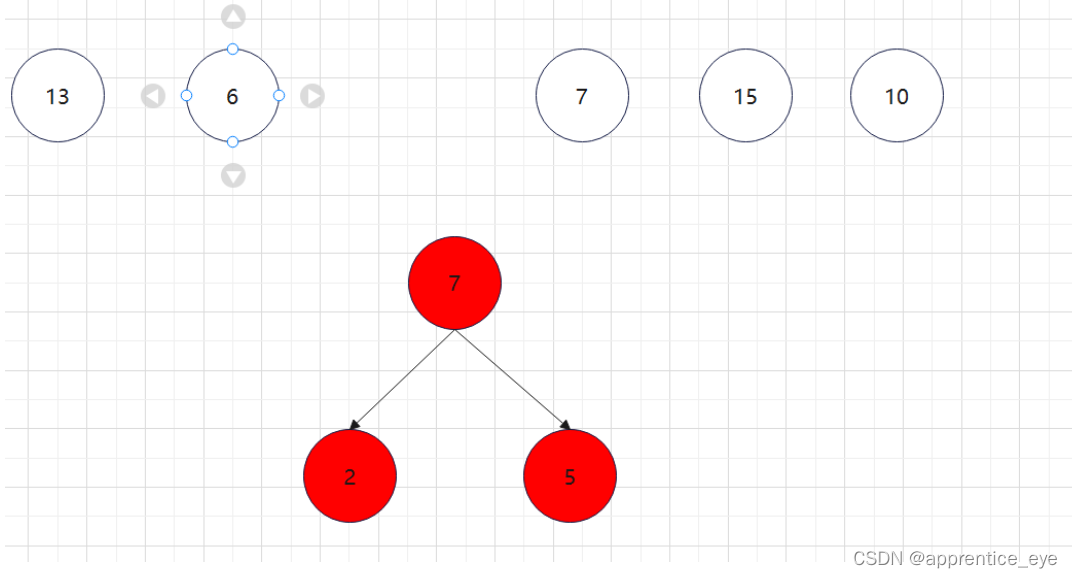
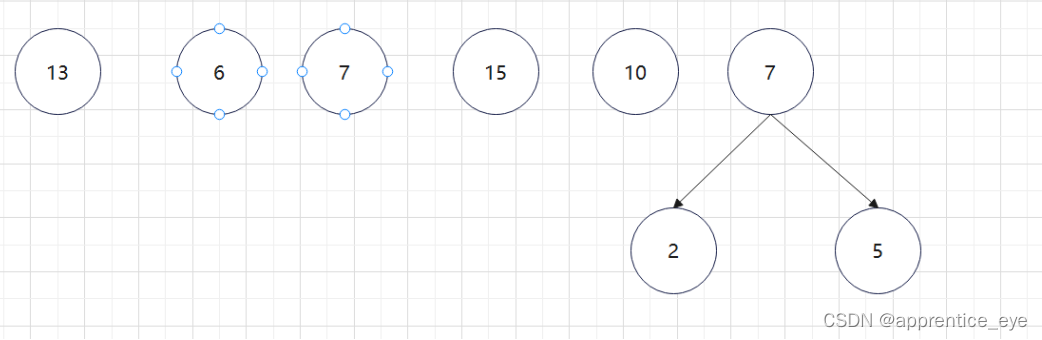
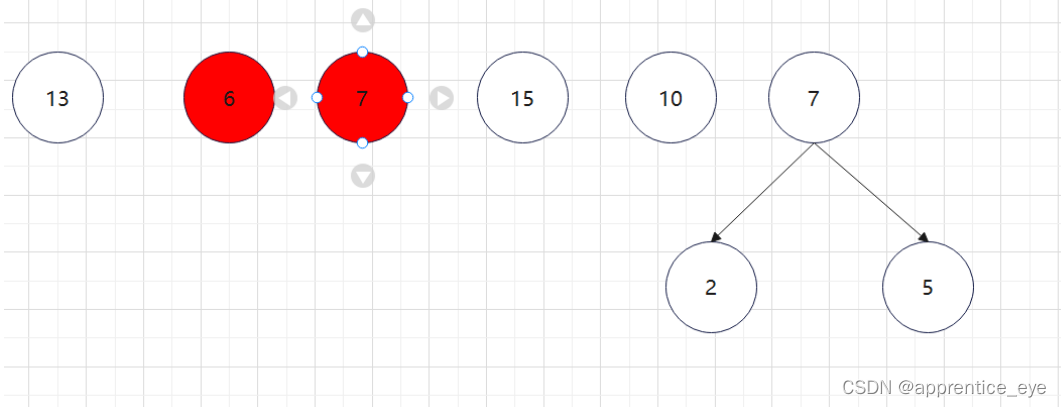
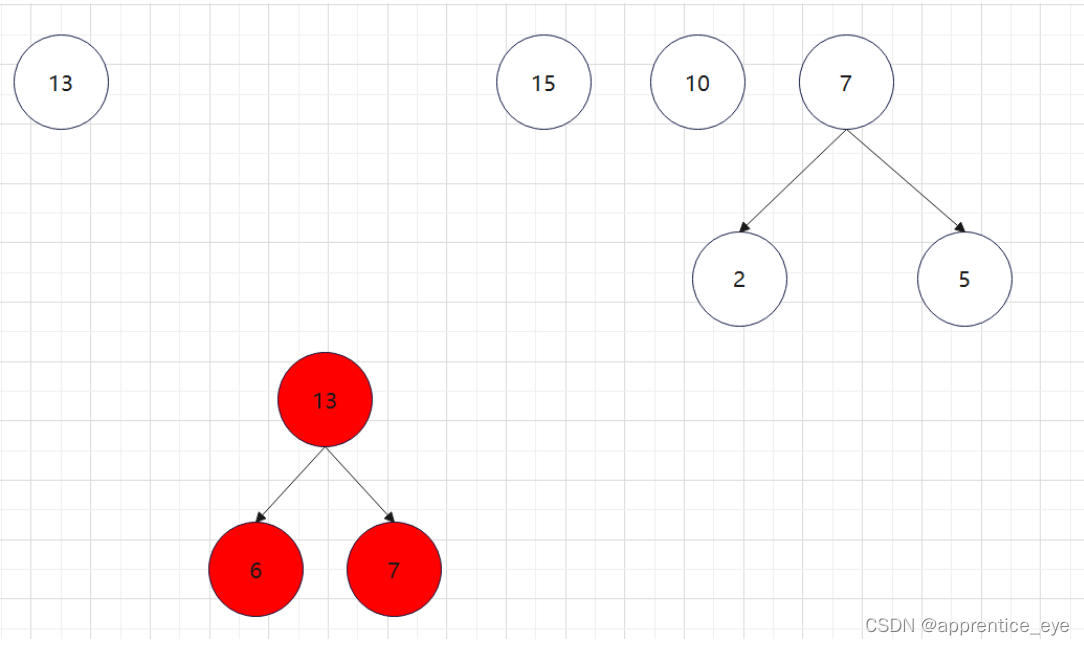
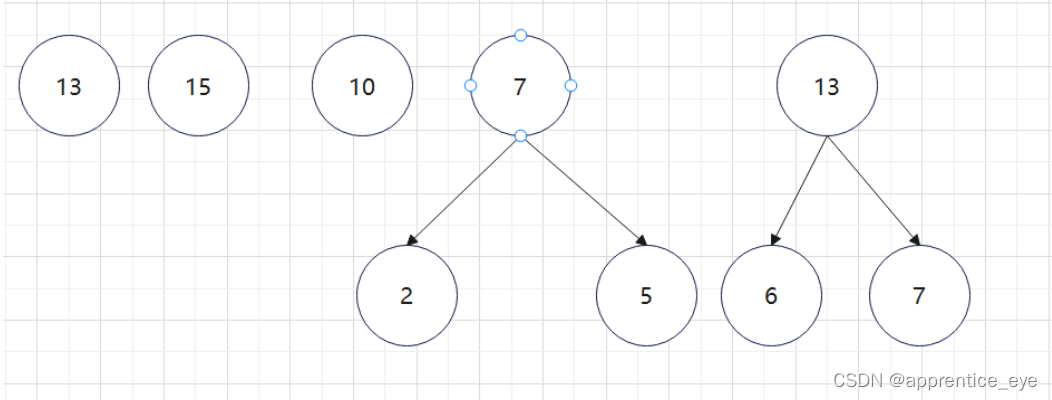
如此进行下去最后只剩下一棵树:
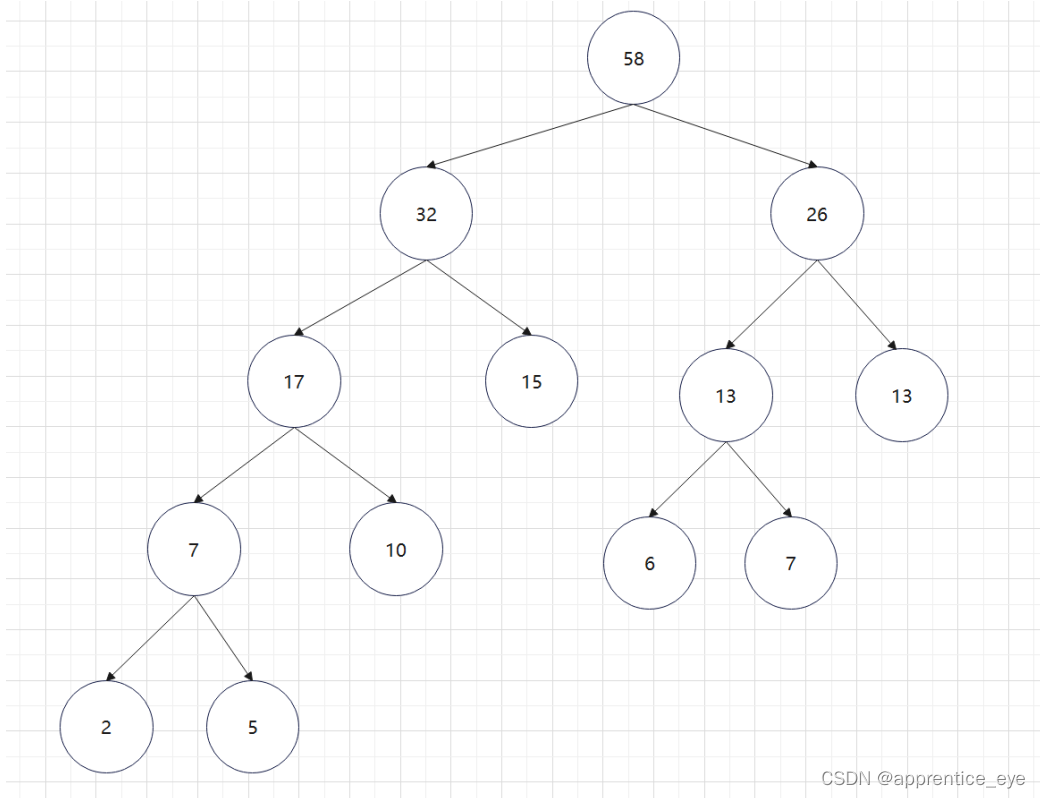
这就是哈夫曼树,所以只需要将字母出现的次数作为权值,按照上述规则我们就能够生成一颗哈夫曼树。代码如下:
#include<stdio.h>
#include<stdlib.h>
struct BinaryTreeNode{int weight;char val;struct BinaryTreeNode * left;struct BinaryTreeNode * right;
};
//对子树按照权值进行降序排列,这样只操作最后面的两棵树就行了
void sort(struct BinaryTreeNode ** p, int length){for(int i=0;i<length-1;i++){for(int j=0; j<length-1; j++){if(p[j]->weight<p[j+1]->weight){struct BinaryTreeNode * t = p[j];p[j] = p[j+1];p[j+1] = t;}}}
}
//创建哈夫曼树
struct BinaryTreeNode * InitHuffmanTree(struct BinaryTreeNode ** p, int length){struct BinaryTreeNode * root = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));while(length!=2){sort(p, length);root->left = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));*(root->left) = *p[length-2];root->right = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));*(root->right) = *p[length-1];root->val = 0;root->weight = p[length-2]->weight+p[length-1]->weight;free(p[length-1]);free(p[length-2]);p[length-2] = root;root = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));length -= 1;}root->left = p[length-2];root->right = p[length-1];root->weight = p[length-2]->weight+p[length-1]->weight;return root;
}
//前序遍历
void preOrderTraversal(struct BinaryTreeNode *root){if(root!=NULL){printf("%d ", root->weight);preOrderTraversal(root->left);preOrderTraversal(root->right); }
}
//中序遍历
void inOrderTraversal(struct BinaryTreeNode *root){if(root!=NULL){inOrderTraversal(root->left);printf("%d ", root->weight);inOrderTraversal(root->right); }
}
int main(){int n;char code[4][20];printf("请问你有多少个字符需要进行编码:");scanf("%d", &n);struct BinaryTreeNode ** p = (struct BinaryTreeNode **)malloc(sizeof(int)*n);printf("请按顺序输入字符与其出现的次数。\n");for(int i=0; i<n; i++){p[i] = (struct BinaryTreeNode *)malloc(sizeof(struct BinaryTreeNode));p[i]->left = NULL;p[i]->right = NULL;printf("请输入字符:");getchar();scanf("%c", &p[i]->val);getchar();printf("请输入字符出现的次数:");scanf("%d", &p[i]->weight);}printf("请确认你刚才输入的信息:\n");for(int i=0; i<n; i++){printf("字符%c,出现%d次\n", p[i]->val, p[i]->weight);}struct BinaryTreeNode * root = InitHuffmanTree(p, n);printf("此哈夫曼树的权值前序序列为:");preOrderTraversal(root);printf("\n此哈夫曼树的中序序列为:");inOrderTraversal(root);return 0;
}
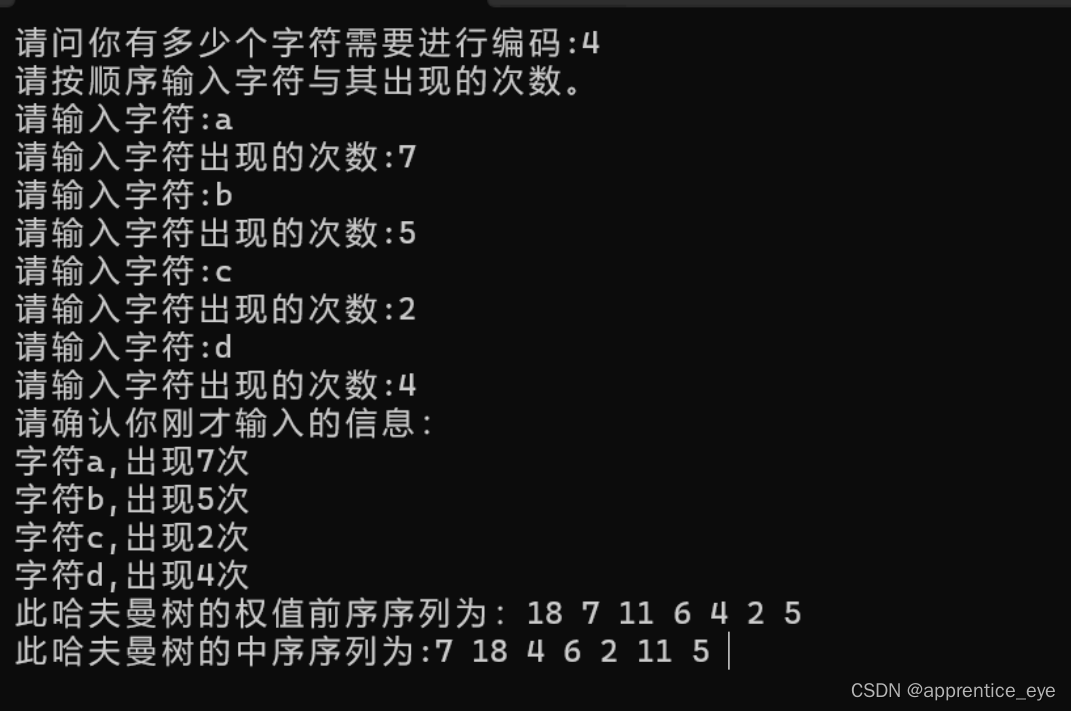
根据权值的前序序列与中序序列可以建立如下二叉树:
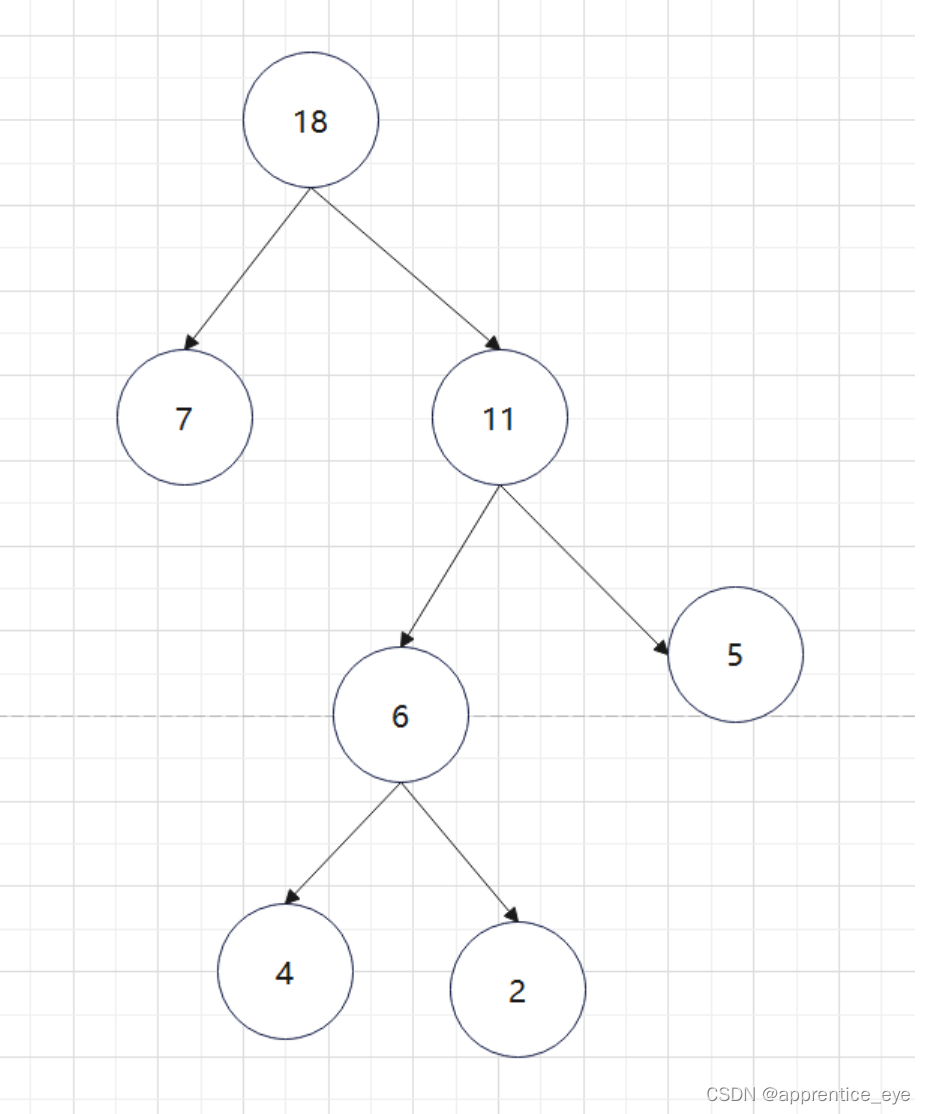
因为出现在叶子结点的才是字符,所以我们可以直到权值为7的结点时’a’,权值为4的结点是’d’,权值为2的结点是’c’,权值为5的结点时’b’,即如下图所示:
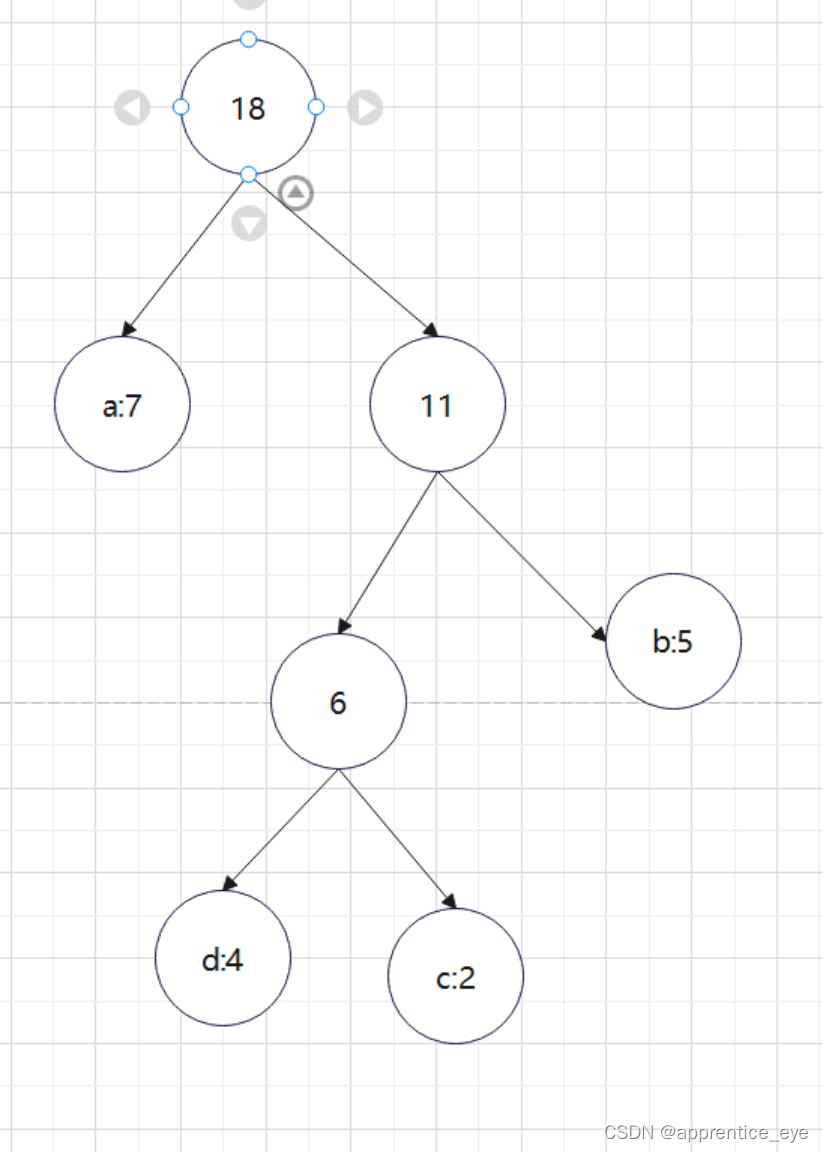
按照哈夫曼树的建立规则进行手动建树,可以建出以下这个树:
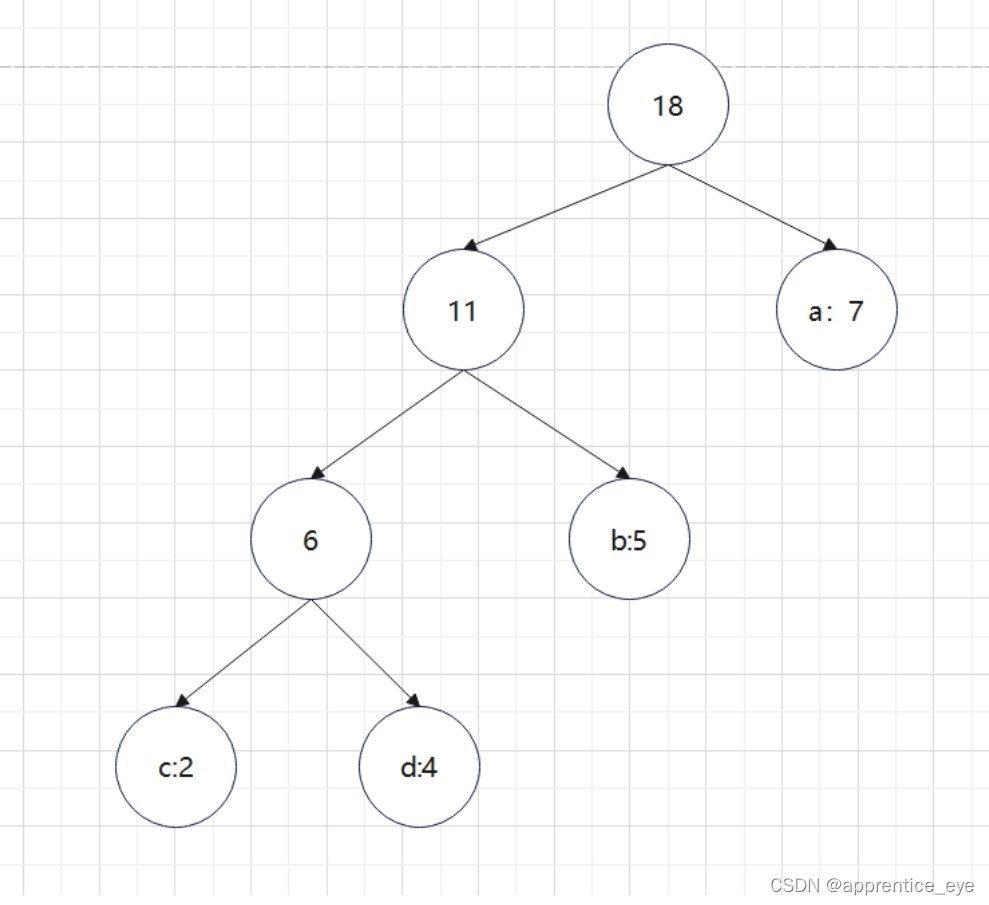
可以看出这两棵树是等价的,只不过是左右孩子交换了下顺序,也就是说明了程序是正确的。接下来就是进行哈夫曼编码了。
向左为0,向右为1进行编码,进行二进制编码,可以写出下面的代码:
void HuffmanCode(struct BinaryTreeNode *root, char n[20], char p[][20], int length){//p用来存储编好的编码if(root!=NULL){switch(root->val){case 'a': case 'b':case 'c':case 'd':int i;for(i=0;i<length;i++){p[root->val-'a'][i]=n[i];}p[root->val-'a'][i]='\0';}n[length++] = '0';n[length] = 0;HuffmanCode(root->left, n, p, length);length--;n[length++] = '1';n[length] = 0;HuffmanCode(root->right, n, p,length);}
}
对上面的树进行编码
运行结果:

可以看到确实生成了哈夫曼编码。
如果有什么地方讲的不好或者讲错的地方欢迎大家指出来,如果我所讲的对你们有帮助不要忘了点赞、收藏、关注哦!
我是你们的好伙伴apprentice_eye
一个致力于让知识变的易懂的博主。
相关文章:

数据结构:树详解
创建二叉树 给出了完整的先序遍历序列,子树为空用’#’表示,所以这样我们在通过先序遍历序列创建二叉树时我们直到先序遍历序列是先进行根结点,然后左子树最后右子树的顺序进行遍历的,所以对于完整的先序遍历序列我们可以直到先序…...
list1.Sort((m, n) => m.Id - n.Id); id是double类型的为什么回报错
问题产生的地方 原因 对于 double 类型的属性,不能直接使用减法运算符进行比较。减法运算符只能用于数值类型,而 double 是浮点数类型。 要在 double 属性上进行排序,可以使用 CompareTo 方法或者使用自定义的比较器。 更改 要在 double 属性…...

GoLang vs Python
Python和Go是两种非常不同的编程语言,它们在设计哲学、用途和特性方面有各自的优势和局限性。以下是它们的一些主要区别: 设计哲学: Python: 设计简洁明了,强调代码的可读性和简洁性。Python遵循"只有一种方式来做一件事"的原则。…...
Hello 2024(A~D,F1)
新年坐大牢 A - Wallet Exchange 题意:共有俩钱包,每回合从其中一个钱包中拿走一块钱,谁拿走最后一块钱谁赢。 思路:奇偶讨论即可。 // Problem: A. Wallet Exchange // Contest: Codeforces - Hello 2024 // URL: https://cod…...

Python+Torch+FasterCNN网络目标检测识别
程序示例精选 PythonTorchFasterCNN网络目标检测识别 如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助! 前言 这篇博客针对《PythonTorchFasterCNN网络目标检测识别》编写代码,代码整洁,规…...

v8 pwn利用合集
文章目录 前置知识JS Object 相关Ignition 相关JIT - turboFan 相关starCTF2019 OOB【越界读写map字段】googleCTF2018 jit【浮点数精度丢失导致越界读写】数字经济线下 Browser【Object::toNumber中callback导致的越界写】前置知识 JS Object 相关 V8 中的对象表示 ==> 基…...

JVM:字节码
JVM:字节码 前言1. JVM概述1.1 JVM vs JDK vs JRE1.1.1 JVM1.1.2 JDK1.1.2.1 常用的JDK8是Oracle JDK 还是 OpenJDK 1.1.3 JRE1.1.4 三者之间的关系与区别 1.2 什么是字节码?采用字节码的好处是什么?1.3 Java 程序从源代码到运行的过程1.4 JVM的生命周期1.5 JVM架…...

常见网络设备及功能详解
网络设备 - 交换机 交换机:距离终端用户最近的设备,用于终端用户接入网络、对数据帧进行交换等。 交换机的功能: 终端设备(PC、服务器等)的网络接入二层交换(Layer 2 Switching) 网络设备 - …...

Python教程(20)——python面向对象编程基本概念
面向对象 类和对象初始化方法属性和方法self关键字继承多态 面向对象(Object-oriented)是一种常用的程序设计思想,它以对象作为程序的基本单元,将数据和操作封装在一起,通过对象之间的交互来实现程序的功能。 在面向对…...
C# Winform教程(一):MD5加密
1、介绍 在C#中,MD5(Message Digest Algorithm 5)是一种常用的哈希函数,用于将任意长度的数据转换为固定长度的哈希值(通常是128位)。MD5广泛用于校验数据完整性、密码存储等领域。 2、示例 创建MD5加密…...

Mongodb使用指定索引删除数据
回顾Mongodb删除语法 db.collection.deleteMany(<filter>,{writeConcern: <document>,collation: <document>,hint: <document|string>} ) 删除语法中,除了指定过滤器外,还可以指定写入策略,字符序和使用的索引。 …...
虾皮怎么选品:虾皮(Shopee)跨境电商业务成功的关键步骤
在虾皮(Shopee)平台上进行跨境电商业务,选品是至关重要的一环。有效的选品策略可以帮助卖家更好地了解市场需求,提高销售业绩和客户满意度。以下是一些成功的选品策略,可以帮助卖家在虾皮平台上取得更好的业务成绩。 先…...
)
QML —— 使用Qt虚拟键盘示例(附完整源码)
示例效果 使用"虚拟键盘"注意 (例子的Qt版本:5.12.4) 注意一: /* 必须在main.cpp开始处加入如下代码,否则无法使用"虚拟键盘" */ qputenv(“QT_IM_MODULE”,QByteArray(“qtvirtualkeybo…...
Nacos 持久化及集群的搭建【微服务】
文章目录 一、统一配置管理二、微服务配置拉取三、配置热更新四、多环境共享配置五、Nacos 集群搭建1. 集群结构2. 初始化数据库3. 搭建集群 六、Nginx 反向代理七、启动项目测试 一、统一配置管理 案例练习的时候我们只有两个微服务,管理起来非常简单,但…...
win10下vscode+cmake编译C代码操作详解
0 工具准备 1.Visual Studio Code 1.85.1 2.cmake 3.24.01 前言 当我们只有一个.c文件时直接使用vscodeCode Runner插件即可完成编译,如果我们的工程很复杂包含多个.c文件时建议使用cmake来生成对应的make,指导编译器完成编译,否则会提示各…...
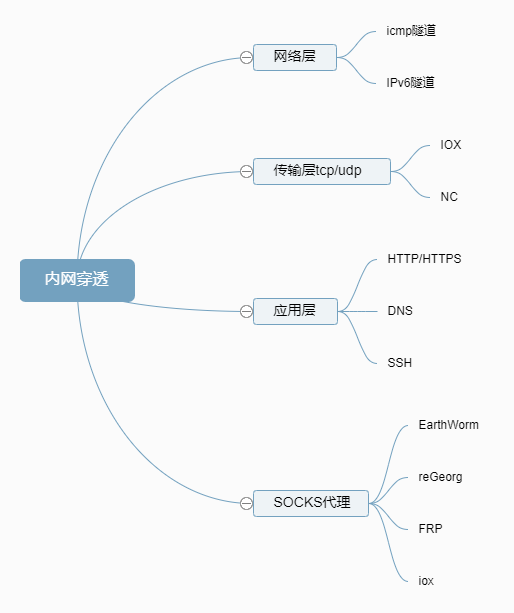
网络安全红队常用的攻击方法及路径
一、信息收集 收集的内容包括目标系统的组织架构、IT资产、敏感信息泄露、供应商信息等各个方面,通过对收集的信息进行梳理,定位到安全薄弱点,从而实施下一步的攻击行为。 域名收集 1.备案查询 天眼查爱企查官方ICP备案查询 通过以上三个…...

【基于openGauss2.1.0企业版安装X-Tuner参数调优工具】
【基于openGauss2.1.0企业版安装X-Tuner参数调优工具】 一、前提条件二、安装X-Tuner 2.1.0: 一、前提条件 已安装了openGauss2.1.0企业版 二、安装X-Tuner 2.1.0: 以root用户登录到服务器 安装以下依赖: yum -y groupinstall "Development tools" yum…...
SpringBoot+Vue轻松实现考试管理系统
简介 本系统基于 Spring Boot 搭建的方便易用、高颜值的教学管理平台,提供多租户、权限管理、考试、练习、在线学习等功能。主要功能为在线考试、练习、刷题,在线学习。课程内容支持图文、视频,考试类型支持考试、练习、问卷。 源码下载 网…...

详解Keras:keras.preprocessing.image
keras.preprocessing.image Keras 库中的一个模块,用于处理和增强图像数据,它提供了一些实用的函数,如图像的加载、预处理、增强等。 常用函数 1、load_img 用于加载图像文件,并返回一个 NumPy 数组表示该图像 示例 from ker…...
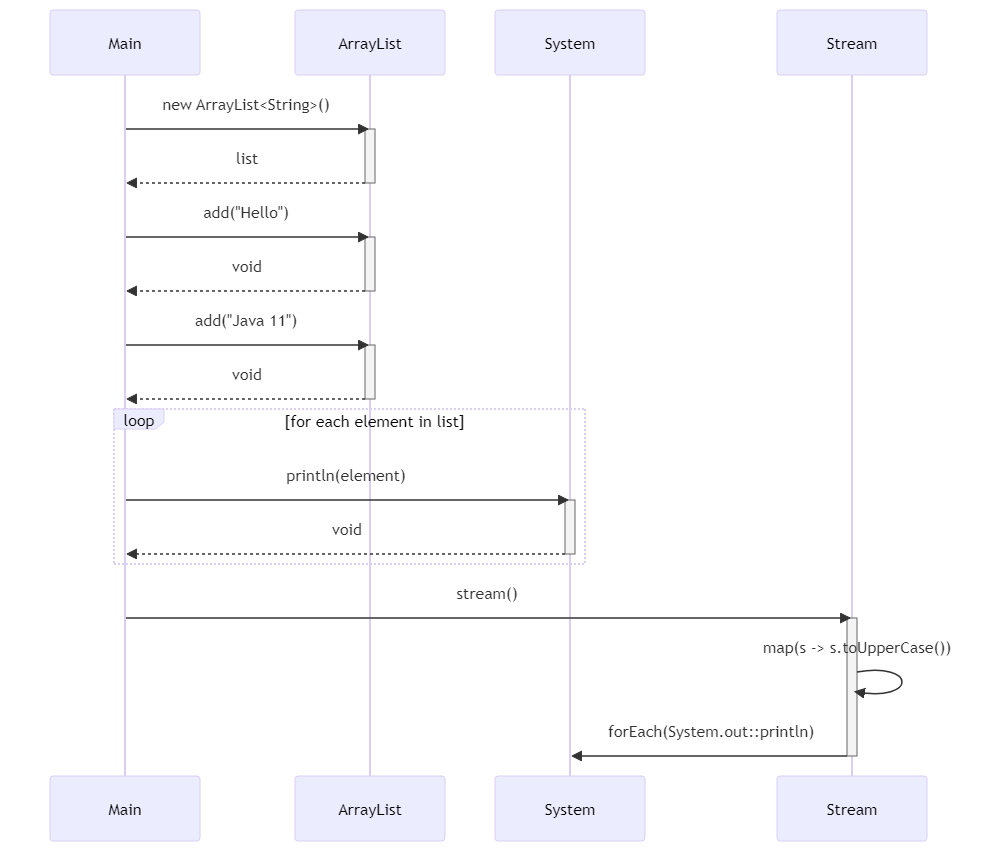
来瞅瞅Java 11都有啥新特性
第1章:引言 大家好,我是小黑!今天小黑要和咱们聊聊Java 11,这个在Java发展史上占有一席之地的版本。说起Java,咱们都知道,它是一门历史悠久又持续发展的编程语言。Java不仅因其“一次编写,到处…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...
