回文链表【链表】
Problem: 234. 回文链表
文章目录
- 思路 & 解题方法
- 复杂度
- Code
思路 & 解题方法
先转成列表。
复杂度
时间复杂度:
添加时间复杂度, 示例: O ( n ) O(n) O(n)
空间复杂度:
添加空间复杂度, 示例: O ( n ) O(n) O(n)
Code
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:def isPalindrome(self, head: Optional[ListNode]) -> bool:l = []while head:l.append(head.val)head = head.nextleft, right = 0, len(l) - 1while left <= right:if l[left] != l[right]:return Falseleft += 1right -= 1return True
相关文章:

回文链表【链表】
Problem: 234. 回文链表 文章目录 思路 & 解题方法复杂度Code 思路 & 解题方法 先转成列表。 复杂度 时间复杂度: 添加时间复杂度, 示例: O ( n ) O(n) O(n) 空间复杂度: 添加空间复杂度, 示例: O ( n ) O(n) O(n) Code # Definition for si…...
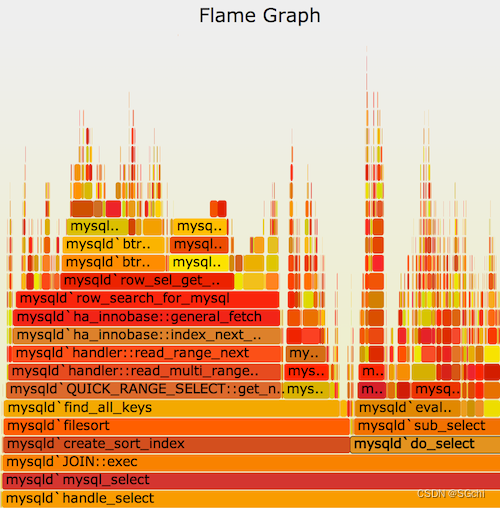
Linux Perf 介绍
文章目录 前言 二、安装Perf三、二级命令3.1 perf list3.2 perf record/report3.3 perf stat3.4 perf top 四、使用火焰图进行性能分析4.1 下载火焰图可视化生成器4.2 使用perf采集数据4.3 生成火焰图参考资料 前言 perf是一款Linux性能分析工具,内置在Linux内核的…...

【论文阅读】Variational Graph Auto-Encoder
0、基本信息 会议:2016-NIPS作者:Thomas N. Kipf,Max Welling文章链接:Variational Graph Auto-Encoder代码链接:Variational Graph Auto-Encoder 1、介绍 本文提出一个变分图自编码器,一个基于变分自编…...
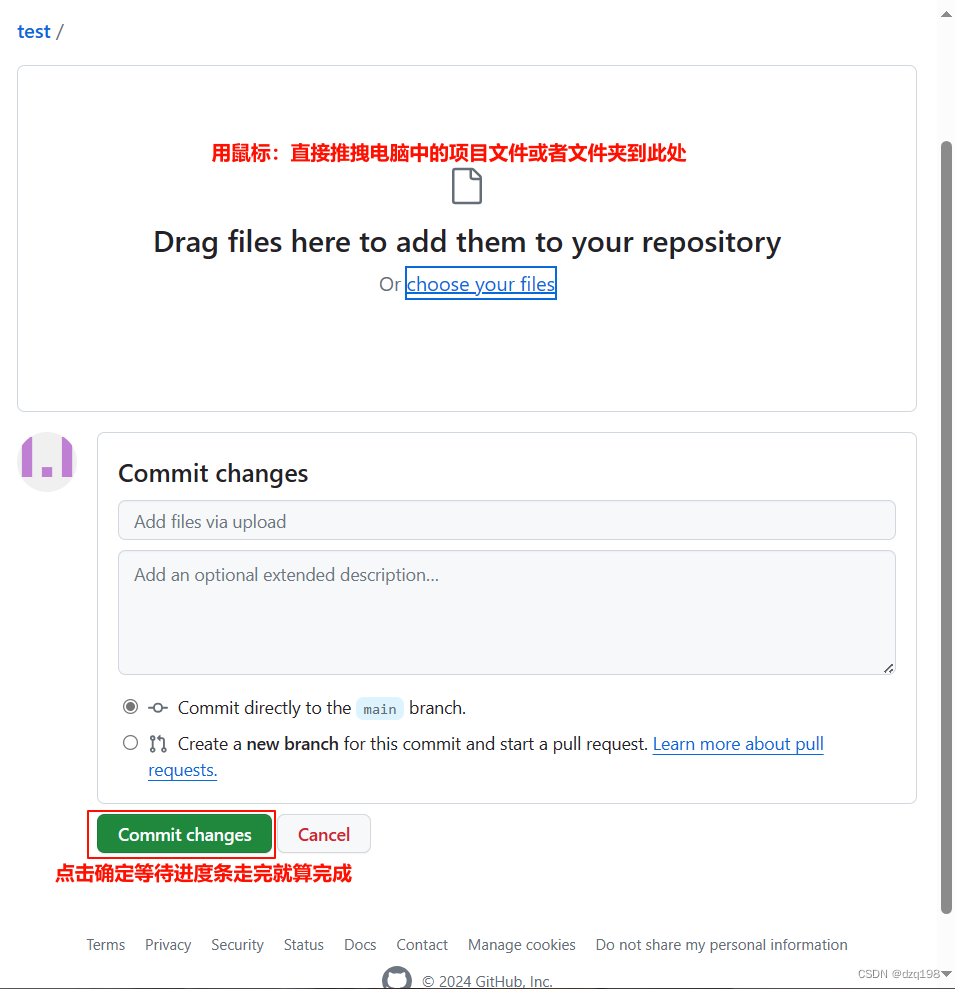
如何把电脑中的项目快速传进Github中?
一、打开GitHub网站:https:github.com 登录自己的个人账号 1.新建一个项目 2.用鼠标直接拖拽电脑中的项目文件夹与文件到新创建的项目中点击保存即可。...
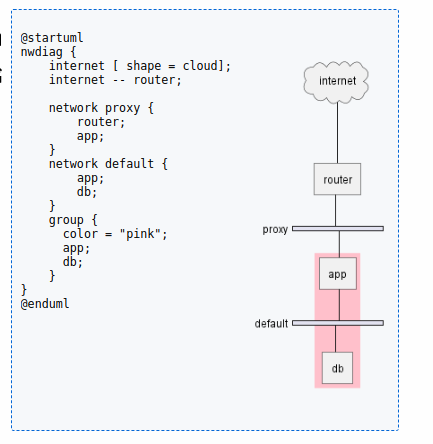
Plantuml之nwdiag网络图语法介绍(二十九)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

MyBatis接口的方法上使用,定义对应的 SQL 操作
目录标题 一、Mapper:二、Select、Insert、Update、Delete:三、Results、Result:四、Param:五、# 和 $: MyBatis 是一款基于 Java 的持久层框架,它通过简化数据库操作来帮助开发者构建更好的数据库访问应用…...

(20)Linux初始文件描述符
前言:本章我们介绍 O_WRONLY, O_TRUNC, O_APPEND 和 O_RDONLY。之后我们开始讲解文件描述符。 一、系统传递标记位 1、O_WRONLY C 语言在 w 模式打开文件时,文件内容是会被清空的,但是 O_WRONLY 好像并非如此? 代码演示&…...
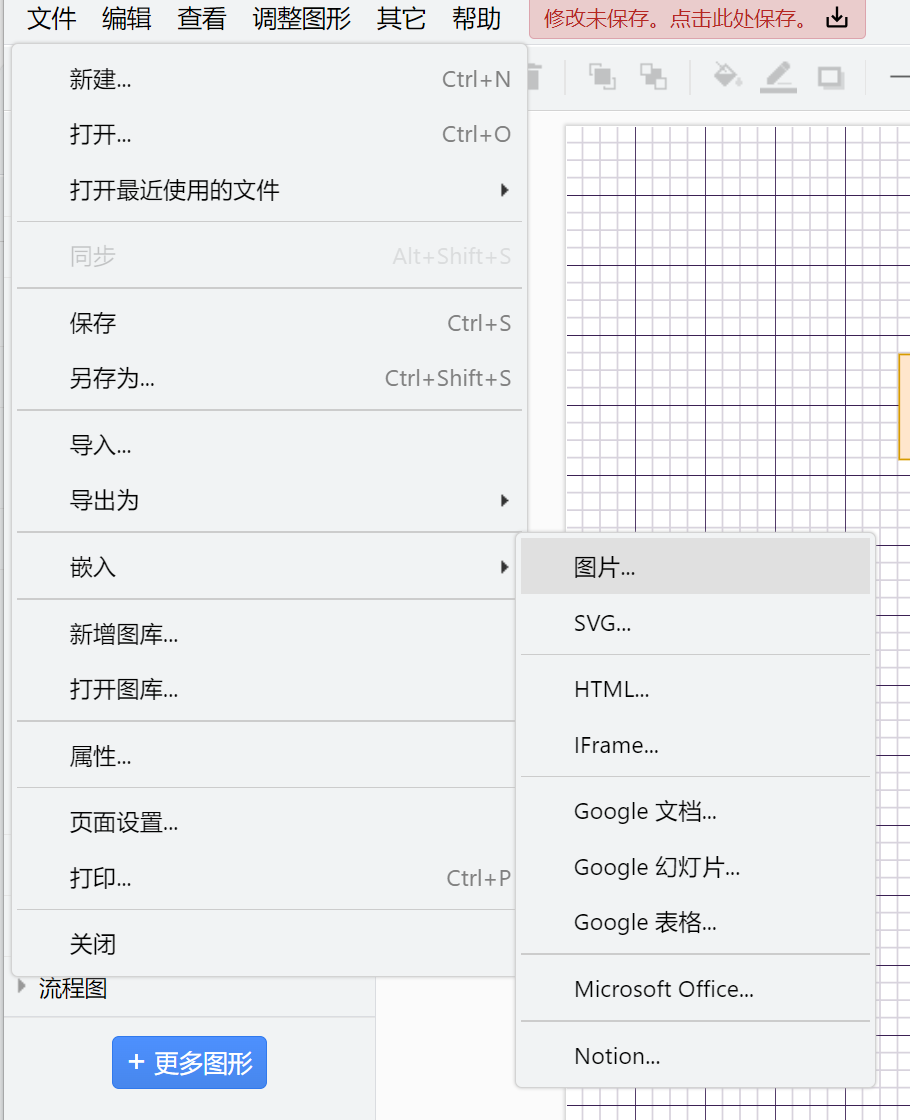
draw.io基础操作和代码高效画图进阶
文章目录 一、基础操作1、链接2、等比例变形3、复制4、插入表格 二、在线打开三、插入—功能聚集地1、插入图片2、插入画笔3、插入布局4、导出 四、图码转换——高效画图1、通用图码转换2、流程图生成:使用mermaid语言生成图: 五、图码转换高效画图的典型…...
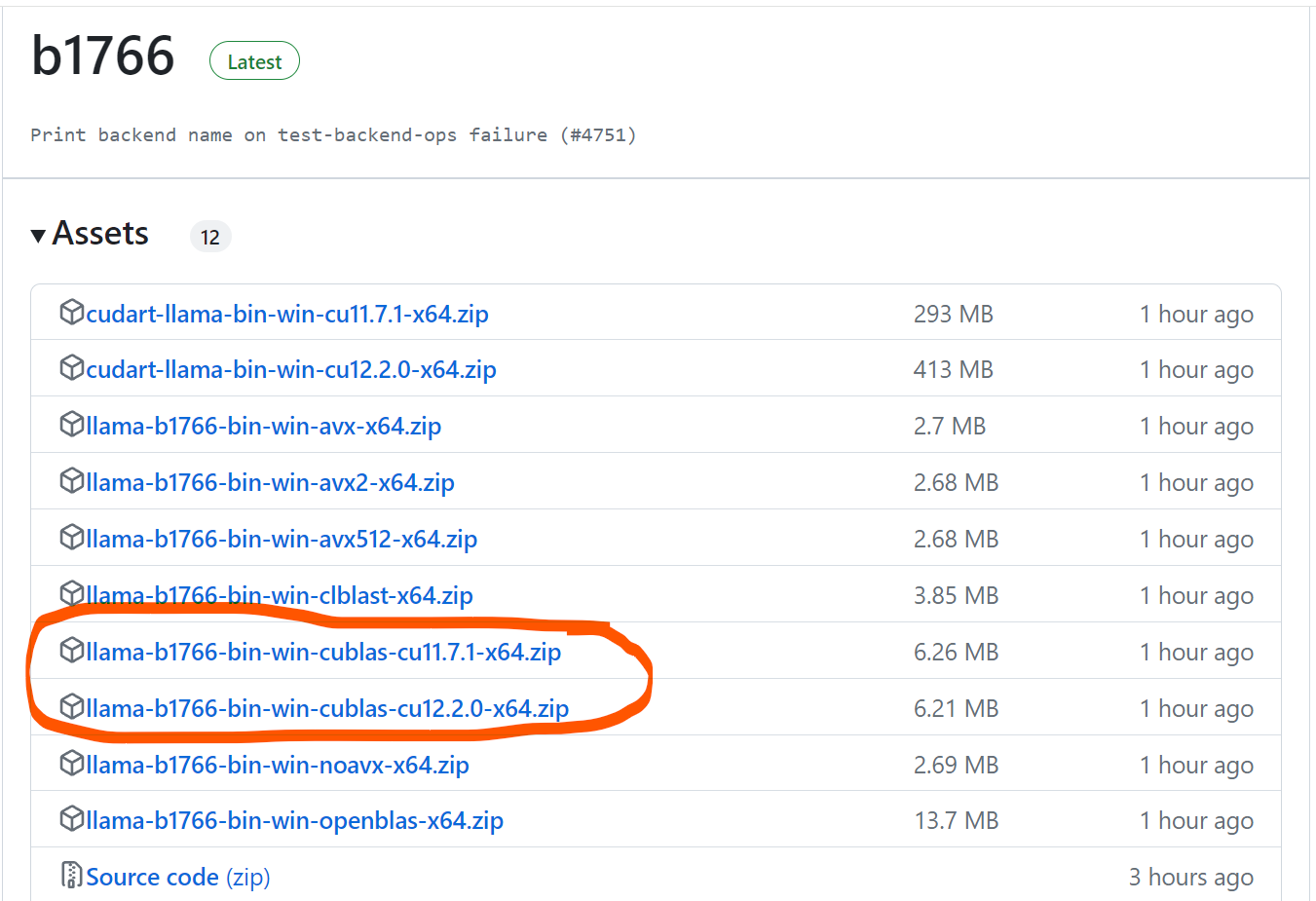
2024-01-04 用llama.cpp部署本地llama2-7b大模型
点击 <C 语言编程核心突破> 快速C语言入门 用llama.cpp部署本地llama2-7b大模型 前言一、下载llama.cpp以及llama2-7B模型文件二、具体调用总结 前言 要解决问题: 使用一个准工业级大模型, 进行部署, 测试, 了解基本使用方法. 想到的思路: llama.cpp, 不必依赖显卡硬件…...

HTTP打怪升级之路
新手村 上个世纪80年代末,有一天,Tim Berners-Lee正在工作,他需要与另一台计算机上的同事共享一个文件。他尝试使用电子邮件,但发现电子邮件不能发送二进制文件。Tim Berners-Lee意识到,他需要一种新的协议来共享二进制…...
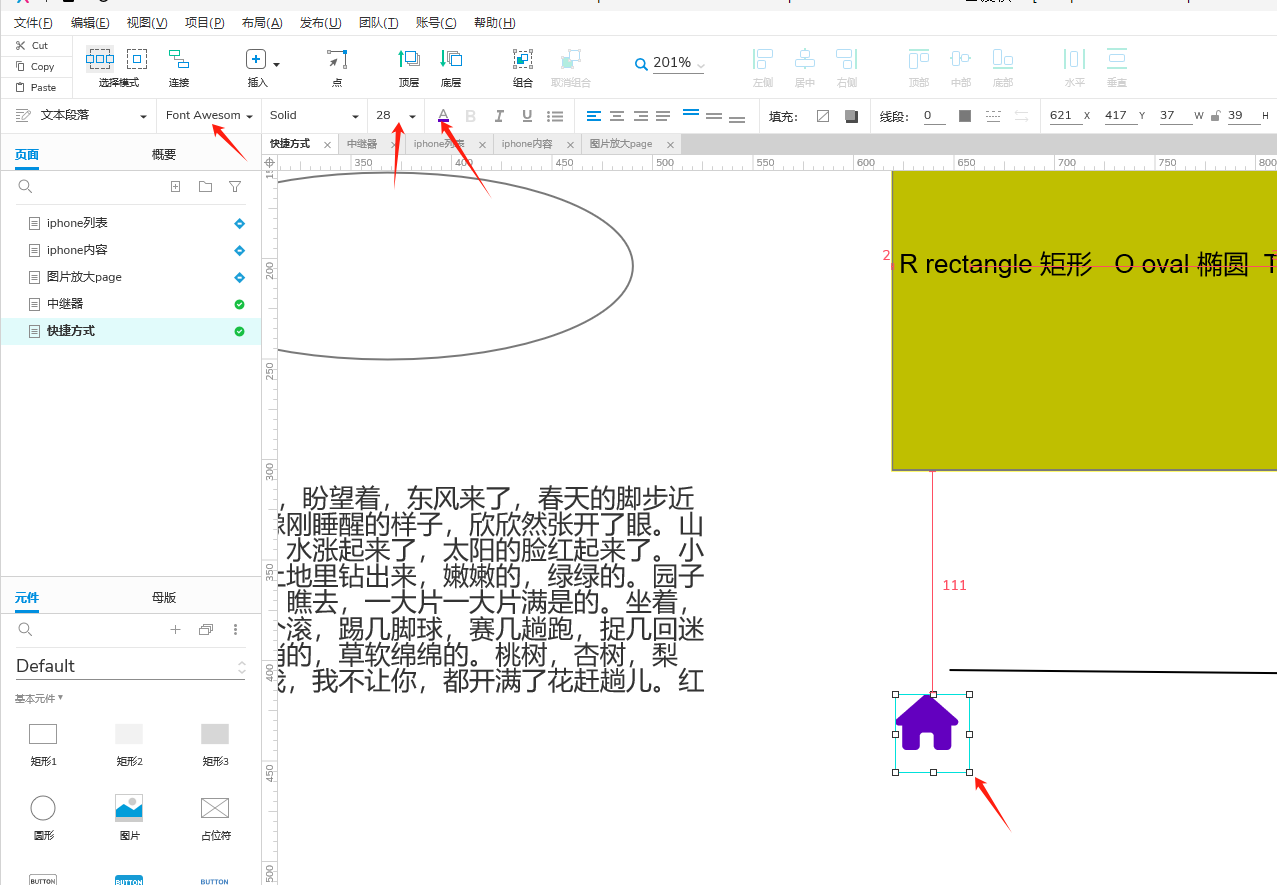
axure RP9.0安装字体图标库fontawesome
字体图库地址: Font AwesomeThe internets icon library toolkit. Used by millions of designers, devs, & content creators. Open-source. Always free. Always awesome.https://fontawesome.com/v6/download进入后下载想要的版本如我是6.3 下载后得到压缩包,解压之后…...

PiflowX组件-ReadFromUpsertKafka
ReadFromUpsertKafka组件 组件说明 upsert方式从Kafka topic中读取数据。 计算引擎 flink 有界性 Unbounded 组件分组 kafka 端口 Inport:默认端口 outport:默认端口 组件属性 名称展示名称默认值允许值是否必填描述例子kafka_hostKAFKA_HO…...
序列号2000-3000)
keil 5 ARM CC编译错误和警告解释大全(3)序列号2000-3000
2001年:已声明虚拟参数,但从未使用过 2002年:虚拟参数重新定义为do变量 2003:无法优化:常量/表达式传递给可能修改的变量 2004:重新维度的数组作为参数传递 2005:重维度数组等价 2006&…...
CentOS 7 实战指南:文件或目录的权限操作命令详解
前言 这篇文章详细介绍了文件和目录的常用权限操作命令,并提供了全面的技术解析。通过本文,你将学习如何使用 chmod 和 chown 命令来管理文件和目录的权限,控制用户和用户组的访问权限。无论你是初学者还是有经验的系统管理员,这…...
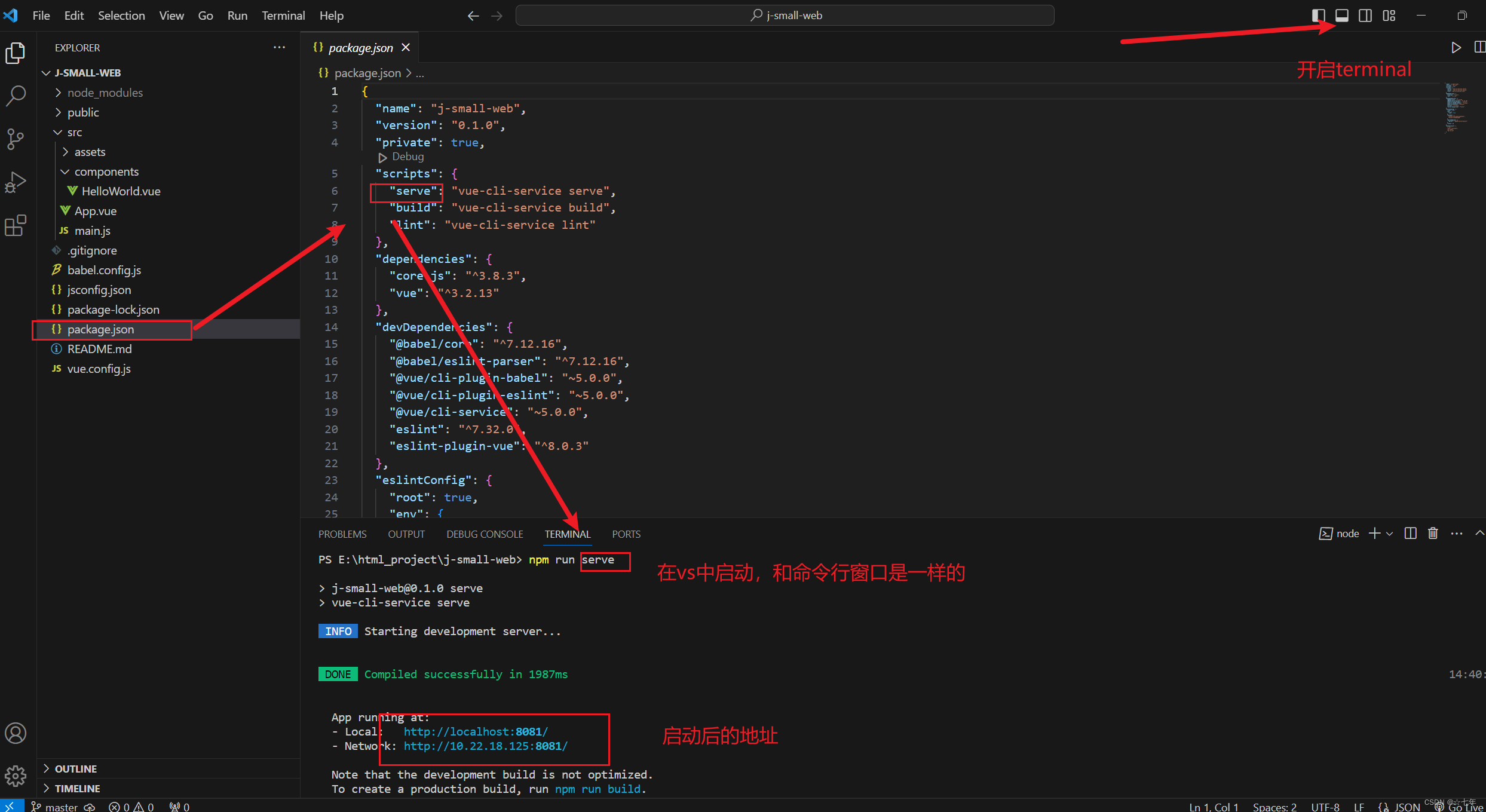
我的第一个前端项目,vue项目从零开始创建和运行
入门前端,从基础做起,从零开始新建项目 背景:VUE脚手架项目是一个“单页面”应用,即整个项目中只有1个网页! 在VUE脚手架项目中,主要是设计各个“视图组件”,它们都是整个网页中某个部分&…...

【OJ】C++,Java,Python,Go,Rust
for循环语法 // cpp// java// python for i in range(集合): for i, val in enumerate(集合): for v1,v2,v3,... in zip(集合1,集合2,集合3,...):Pair // cpp pair<int, string> first second // java Pair<Integer, String> first() new Pair<>(firstVal…...

Flink 任务指标监控
目录 状态监控指标 JobManager 指标 TaskManager 指标 Job 指标 资源监控指标 数据流监控指标 任务监控指标 网络监控指标 容错监控指标 数据源监控指标 数据存储监控指标 当使用 Apache Flink 进行流处理任务时,可以根据不同的监控需求,监控…...

Go语言程序设计-第7章--接口
Go语言程序设计-第7章–接口 接口类型是对其他类型行为的概括与抽象。 Go 语言的接口的独特之处在于它是隐式实现。对于一个具体的类型,无须声明它实现了哪些接口,只要提供接口所必须实现的方法即可。 7.1 接口即约定 7.2 接口类型 package iotype …...

性能优化-OpenMP基础教程(二)
本文主要介绍OpenMP并行编程技术,编程模型、指令和函数的介绍、以及OpenMP实战的几个例子。希望给OpenMP并行编程者提供指导。 🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:高性能(HPC&am…...

让电脑变得更聪明——用python实现五子棋游戏
作为经典的棋类游戏,五子棋深受大众喜爱,但如果仅实现人与人的博弈,那程序很简单,如果要实现人机对战,教会计算机如何战胜人类,那就不是十分容易的事了。本文我们先从简单入手,完成五子棋游戏的…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
